2. 北京市气象局, 北京 100089;
3. 成都信息工程学院, 成都 610225
2. Beijing Meteorological Bureaus, Beijing 100089;
3. Chengdu University of Information Technology, Chengdu 610225
X波段信号在降水估测中的衰减问题比起S波段和C波段较为严重,散射模拟计算指出: X波段电磁波的单程衰减率(AH)分别是C、 S波段的7~ 8倍和10倍以上(Park et al.,2005a)。但是,X波段双偏振天气雷达具有价格低廉、 天线体积小、 易于移动、 空间分辨率较高等优点,并在定量估测降水和粒子的相态识别中,有着非常明显的优势。自从协同自适应大气探测研究中心(Collaborative Adaptive Sensing of the Atmosphere,CASA)利用多部X波段双偏振雷达组建低价位、 高分辨率、 高密度的雷达网络,用于克服传统天气雷达的分辨率和覆盖范围的限制,X波段双偏振气象雷达的研究与应用又再次成为气象雷达研究的热点。X波段双偏振雷达进行定量降雨探测时,仍能继续发挥其独特的重要作用,而衰减引起的误差又不容忽视。因此,必须寻求对反射率(ZH)和差分反射率(ZDR)进行衰减订正的有效方法。
早期反射率的衰减订正研究是从C波段气象雷达开始的,根据衰减和降水的经验公式,利用实际降水量的大小来调整反射率值,再反推衰减率大 小,但是Z-R关系本身的不确定性导致了这种方法的不稳定性(Hitschfeld and Bordan,1954; Smyth and Illingworth,1998)。20世 纪90年代初,Bringi et al.(1990)通过散射模拟发现衰减率(AH)和差分衰减率(ADP=AH-AV)与单位差分传播相移(KDP)呈线性关系,提出双偏振雷达可能通过雷达测量的KDP实现ZH和ZDR的衰减订正。此后,许多学者(Ryzhkov and Zrni,1995; Smyth and Illingworth,1998)对此进行了大量的研究,他们提出了基于差分传播相移的订正方法,因KDP具有独立于雷达系统定标、 受自然状态下的雨滴谱分布(DSD)变化影响较小、 没有雨区衰减效应和波束传播阻碍效应等优势(Zrni and Ryzhkov,1996),短波长双偏振气象雷达的衰减问题可以得到较好的解决。此外,一个相对优势的条件是: 通过散射模拟实验发现,X波段雷达的KDP分别是C波段、 S波段雷达的1.5、 3.0倍。但此法的局限性是,对于X波段雷达,如果电磁波在大雨滴区或者冰水混合区传播,水平和垂直方向的电磁波之间会形成差分散射相移(δ),这时雷达测量到的差相移是由差分传播相移(ΦDP)和差分散射相移(δ)组成,而单位差分传播相移(KDP)就是利用差分传播相移估计获得的。因此,δ的出现与变化将会影响到ΦDP,进而影响到KDP的精确估计。不过,可以采用特定的滤波器消除δ的影响,如Hubbert et al.(1993)通过设计低通滤波器对回波的ΦDP进行滤波,1995年他们又在此基础上,利用多次迭代的方法,基本上消除了δ的影响(Hubbert and Bringi,1995)。
在衰减订正方法研究中,由于雨滴谱(尤其是当存在直径大于2.5 mm的大粒子时)、 温度、 形状等因素的影响,AH~KDP和ADP~KDP关系的经验公式中系数变化比较大。许多学者(Jameson,1992; Ryzhkov and Zrni,1995; Smyth and Illingworth,1998; Carey et al.,2000; Tesud et al.,2000; Le Bouar et al.,2001)对此进行了广泛而深入的研究,他们探讨了粒子大小、 温度、 形状等因素对AH~KDP和ADP~KDP关系的经验公式中系数的影响,将订正方法从固定系数法发展为变系数法。虽然这种方法能够提供比较稳定的衰减订正,但是采用由数值模拟或者几次观测拟合所得到的系数,仍然存在着较大的误差。21世纪初,Bringi et al.(2001)提出自适应约束算法,并用C波段雷达资料对此进行了验证分析,结果表明这是一种相对较好的方法。此后,Park et al.(2005a,2005b)和Gorgucci et al.(2005,2006)改进了自适应约束算法,对X波段双线偏振雷达的衰减订正问题进行了探讨。何宇翔等(2009)引入卡尔曼滤波到差分传播相移滤波中,对车载X波段偏振雷达观测层状云降水进行衰减订正,并给出了订正方法的适用范围为: 主要是稳定的降水云,且近地面降水粒子的主轴是水平取向。胡志群等(2008)比较了KDP订正法、 ZH订正法,指出KDP订正法要优于ZH订正法,但是当KDP较小时,订正存在的误差较大,最后通过设置KDP的阈值,提出综合利用两种订正方法。但该方法仍采用固定的系数对不同的降雨类型进行衰减订正,且只用M\|P分布验证了订正效果。在国内采用自适应约束算法进行衰减订正的研究还未见报道。
中国科学院大气物理研究所中层大气与全球环境探测重点实验室在双波长雷达基础上进行X波段雷达的双偏振升级改造以来,结合研究项目进行了多年的观测。为了更充分地利用该雷达的偏振特性,更深入进行云、 降水等研究,本文在综合分析了多种订正方法优缺点前提下,选择了以自适应约束算法为基础,并做些改进,结合中层大气与全球环境探测重点实验室X波段雷达的特点,提出该雷达反射率的衰减订正方法。为了能推广使用这个订正方法,我们采用比较严格的比对方法进行验证。下面将介绍所采用的订正方法及验证对比分析结果。
2 订正方法
自适应约束算法(Self\|consistent method with constraints)是Bringi et al.(2001)扩展了Testud et al.(2000)降雨廓线(ZPHI)算法与Smyth and Illingworth(1998)方法得出的: 这是一种利用雷达参数本身,通过不断调整,得到AH~KDP关系中的最佳系数,该衰减订正方法综合考虑了雨滴谱、 粒子形状、 温度等因素的影响。Park et al.(2005a,2005b)利用散射模式计算出X波段双偏振雷达AH~KDP、 AH~ZH参数中的系数关系,发展自适应约束算法对X波段双偏振雷达进行衰减订正,并通过比较双偏振参数之间关系验证了该方法的优越性。本文基于Park et al.(2005a)的研究结果,结合本实验室雷达的特点给出一种较适用的订正方法。
雷达反射率衰减订正的本质是如何准确地估计雨区衰减率AH,如公式(1)所示:
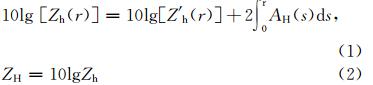
式中
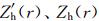 分别为订正前后的反射率值(单位: mm6/m3),AH为单程衰减率(单位: dB/km),ZH的单位为 dBZ。
分别为订正前后的反射率值(单位: mm6/m3),AH为单程衰减率(单位: dB/km),ZH的单位为 dBZ。
在自适应约束算法中,假如一个雨区径向范围是从r0 到r1(r0
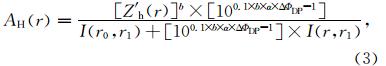
其中,
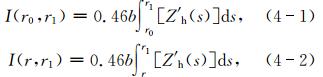
式中,
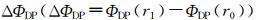 为雨区范围内的差分传播相移的变化总量,系数b通过以下散射模式的经验公式获得,即:
为雨区范围内的差分传播相移的变化总量,系数b通过以下散射模式的经验公式获得,即: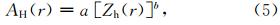
式中,AH和Zh的关系是在假定雨滴谱为gamma分布的前提下,经散射模式得到的(Testud et al.,2000)。计算表明,指数b在给定的频率下,变化较小,比起双极化参数(KDP和ZDR)对粒子的形状和温度敏感性弱一些。Delrieu et al.(2000)曾给出X波段,指数b的变化范围为0.76到0.84,据此本文设定b的值为0.8。此外,(3)式中的α也可通过散射模式的经验公式(6)获得:
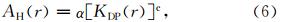
式中KDP的单位是(°)/km。该式需满足的前提条件是: AH和KDP(ΦDP)成线性关系。实际上,通过散射模拟得到在2.8~9.3GHz频率范围内,AH和KDP存在良好的线性关系(Bringi et al.,1990)。
研究发现,α随着温度和粒子形状的变化范围非常大。Carey et al.(2000)指出,在X波段,α的变化范围是0.139 dB ·(°)-1到0.335 dB ·(°)-1。若以单一的固定系数α来计算AH,势必带来较大误差,从而影响ZH的订正结果。
为了减小系数α的影响,自适应约束算法的一般做法是,预先从散射模式计算出的系数范围内找到最佳α值。综合考虑Park et al.(2005a)和何宇翔(2009)的散射模式模拟结果后,本文设定α的取值范围为0.13~0.35,除在中心区0.24~0.26区间内,步长选为0.005,其它区域步长为0.01。最佳α的选取步骤如下:
第一步: 对每一个α值,通过(3)式计算出AH(r,α),根据衰减总量一定要与该雨区的差分传播相移变化总量相一致的约束条件,可以利用AH通过下式重构出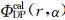 :
:
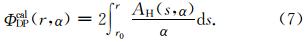
第二步: 用下式比较
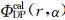 和雷达实际测量的ΦDP(r),以
和雷达实际测量的ΦDP(r),以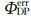 值最小作为约束条件获得最佳的α值。
值最小作为约束条件获得最佳的α值。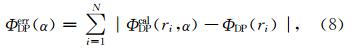
其中,i为从雨区开始r0到雨区结束r1的距离库数。
订正时只要将得到的最佳系数α代入(3)式计算出AH,再将AH代入(1)式,即可实现该帧ZH订正。通过比较路径衰减积分和雷达实际测量的ΦDP(r)得到最佳系数α是自适应约束算法的最大特点。
3 X波段双线偏振雷达
本文使用的是中国科学院大气物理研究所中层大气与全球环境探测重点实验室X波段双线偏振雷达(IAP\|Radar)2009年的观测资料。该雷达采用双线偏振体制,单路交替发射/接收水平或垂直电磁波。该体制是在原单偏振雷达的基础上升级而成(段树等,2002)。系统主要参数见表 1。
|
|
表 1 IAP\|Radar主要参数 Table 1 System characteristics of the IAP\|Radar |
2009年7月31日北京地区经历了一次强降雨过程。观测资料显示,北京时间03:00~03:06时段的雨区位于X波段雷达和S波段雷达作对比的最佳观测范围内,故选取该时段的雷达反射率体扫数据进行衰减订正。
订正之前,本文先用Hubbert et al.(1993)和Hubbert and Bringi(1995)的方法对雷达测量的差相移 C进行预处理和质量控制,滤除了后向差分散射相移δ,如公式(9)所示。并对反射率ZH进行了质量控制。
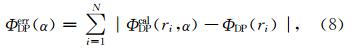
再利用自适应约束算法对该过程进行衰减订正。根据雷达数据的特点,先分析了一帧数据(仰角3°,方位角115°)的衰减订正情况,该数据刚好位于强对流区域的中心,在此径向方向上对应的雨区范围是从25~85 km。
图 1所示,虚线为25~85 km距离内测量的差相移(C),实线是利用FIR低通滤波器滤波过后的效果。在25~60 km距离内,C变化增长比较缓慢,起伏较小,滤波效果很好; 在60~75 km距离内,C变化增长比较快,起伏较小,滤波后完全与测量趋势符合,ΦDP从46°增加到100°; 在75~85 km 距离内,由于前面经历了强回波区,电磁信号衰减严重,雷达实际 C起伏较大,经过滤波后ΦDP依然有一定的起伏,但就整体而言,影响不大。
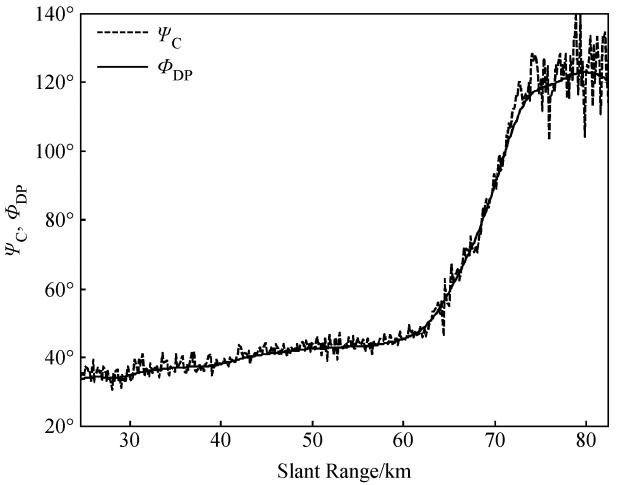 | 图 1 差相移 C(虚线)和滤波后差分传播相移ΦDP(实线)Fig. 1 The differential phase shift(C)(dashed line) and differential propagation phase shift(ΦDP)after filtering(solid line) |
图 2给出订正前后反射率的变化曲线,虚线为订正前的反射率值,实线为订正后的反射率值,可以看出,在25~45 km范围内,因降雨强度小,衰减量较小,订正前和订正后基本上没有差别; 40~65 km范围内,电磁波经20 km以上雨区的衰减,订正后的反射率曲线比订正前高出2~5 dB; 60~85 km范围内,电磁波经历了强对流雨区过程,且电磁波已经传播了将近40 km的距离,订正后比订正前高出10~20 dB,其中65~75 km范围内,订正后的反射率值达到50 dBZ以上。这与ΦDP的变化趋势是一样的。
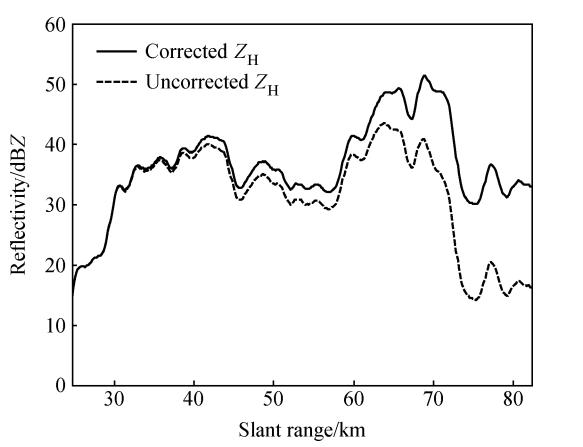 | 图 2 订正前后雷达反射率值的比较(方位角115°)Fig. 2 Comparison of radar reflectivity before and after correction(azimuth angle 115°) |
图 3(见文后彩图)是订正前X波段雷达组合反射率的PPI(Plane Position Indicator)图,在离IAP\|Radar站较近的范围内,雨区衰减较少,反射率多为20~40 dBZ,例如顺义东北20~30 km范围内,反射率分布比较均匀,约为20~40 dBZ; 在60 km以外,订正前雷达图上基本未发现有对流性回波,反射率值均在35 dBZ以下,密云—平谷—蓟县一带都在20~30 dBZ的范围内,蓟县—香河—廊坊一带,反射率值为20~35 dBZ,在较远的区域反射率值更低。
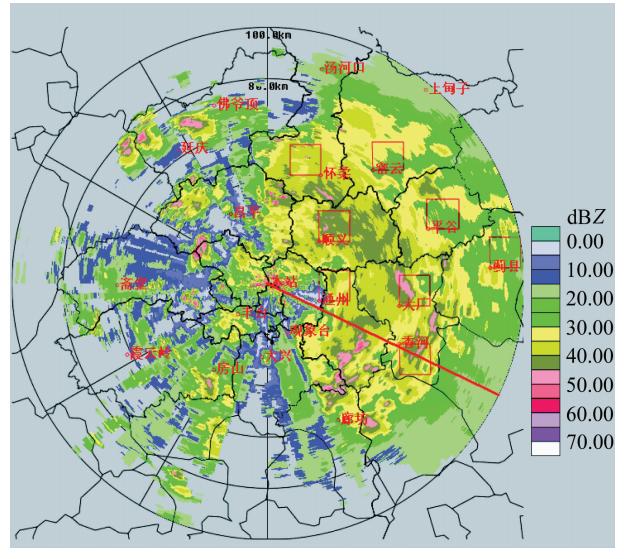 | 图 3 订正前X波段雷达组合反射率 (2009年7月31日02:59:44 BJT)Fig. 3 PPI of X-band radar composite reflectivity before correction at 02:59:44 BJT (Beijing time) 31 Jul 2009 |
对比订正前后的反射率分布 [图 3与图 4(见文后彩图)] 后,可以看出,在雷达站30 km范围以内,订正前后基本上没有差别; 随着雨区距离的增加,在30~60 km范围内,电磁波信号的衰减,订正后略微有一些差别,在怀柔—顺义—大厂一带,订正后的反射率值比订正前高一些,出现零星的对流; 在60 km以外较远的区域,在密云—平谷一带,订正后反射率值比订正前高出5~10 dB左右,出现零星的对流区。特别是,在蓟县—香河—廊坊一带出现了明显的强对流区,订正后的比订正前反射率要高出10~15 dB; 在更远的区域,订正后反射率整体上得到加强。总之,订正前后的组合反射率变化很大,而且符合ΦDP的变化趋势,订正效果非常明显。
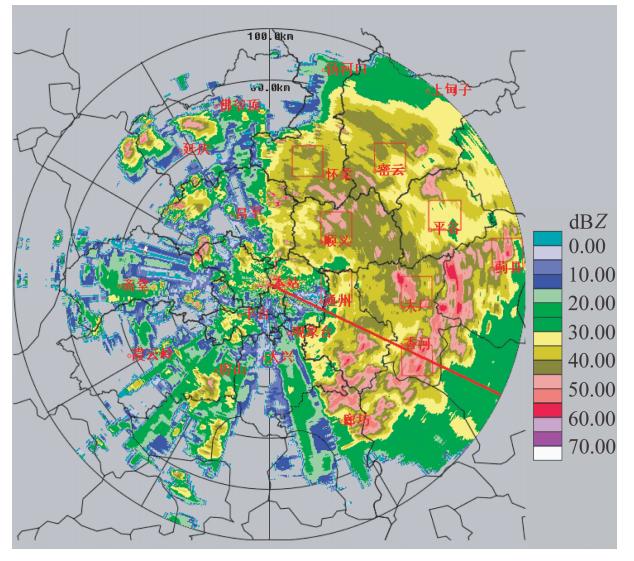 | 图 4 同图 3, 但为订正后Fig. 4 Same as Fig. 3, but after correction |
为了验证本订正方法的效果,我们将订正后的结果与北京市气象局S波段雷达观测值进行详细的对比,其次,还综合分析了AH~ZH和AH~KDP之间的关系,并根据弱对流性与强对流性两种不同的降雨类型,拟合了不同的系数,再与Park et al.(2005a)通过散射模拟得到的结果进行对比,以达到进一步验证订正方法的目的,最后引入地面实测降雨资料,粗略地与订正前后的X波段雷达反射率进行了比较。
5.1 与S波段雷达对比
Ch and rasekar et al.(2006)认为S波段雷达基本上不存在雨区衰减,除非在一些湿雹区。他们还分析了S波段和X波段对比的可能性,指出在瑞利散射下,反射率值不会因频率的变化而变化,但随着滴谱直径的增加,因电磁波频率的不同,米散射的反射率数值也会不同,当反射率值达到30 dBZ以上,X波段雷达测量的反射率值略微比S波段雷达高一些。Matrosov et al.(2006)解释了当反射率高于40 dBZ的时候,X波段雷达测量值要比S波段雷达高2~3 dBZ左右。Anagnostou et al.(2006)在 KAMP项目中,将一部车载X波段双偏振雷达与WSR\|88D雷达进行了粗略的比较,分析了X波段雷达订正效果,但未指出X波段和S波段雷达测量的不同之处。我们在此进行了详细的对比验证,所用S波段资料是北京市气象局的CINRAD/SA雷达数据,该雷达系统具备完善的机内定时自动在线标定、 标校的能力。
S波段雷达位于X波段雷达的东偏南方向,方位角为157°,两部雷达间的直线距离为20.3 km,因为两部雷达之间是北京市城区,高楼较多,X波段雷达遮挡比较严重,综合考虑到两部雷达的位置和周围地物的情况,观测的最佳区域为: 以X波段雷达为中心,方位角30°~150°的范围。
本次对比过程选择在2009年7月31日,X波段雷达观测时间为02:59:44~03:06:12(北京时,下同),S波段雷达观测时间为03:00:00~03:06:00,两者起始时间相差16秒,结束时间相差12秒,两部雷达观测时间在最佳对比区域范围内,适宜进行对比研究。
图 5(见文后彩图)是去除仰角0.5°和1.4°两层之后的S波段雷达组合反射率PPI图,对比图 4和图 5,可以看出,在降雨的范围和趋势上存在较高的一致性: 在较近的区域内,如顺义的东北方向,X波段雷达订正后出现零星的对流区,略微比S波段雷达高一些; 较远的区域,如密云—平谷一带,订正后的值和S波段雷达基本一致,反射率值分布在30~40 dBZ范围内,在具体的区域,因X波段雷达分辨率高,探测的精细一些; 在蓟县—香河—廊坊一带,订正后X波段出现强对流区,强对流区ZH分布在45~55 dBZ,区域范围和位置大小均与S波段雷达一致,X波段的ZH要比S波段雷达大一些,这一差别可能的原因前面已有讨论,不再重复。需要注意的是,图 4和图 5两幅图是以各自雷达站所在地为中心的PPI图,故不能简单用相对雷达站的方位、 距离进行对比,而要用其所在地理位置进行比对。
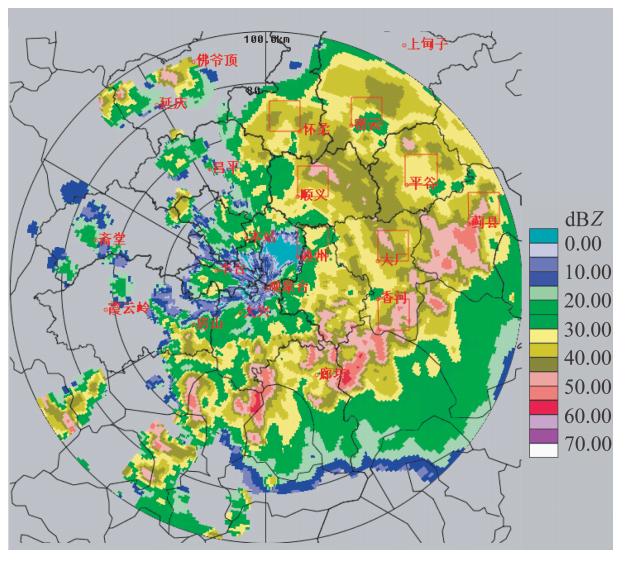 | 图 5 S波段雷达组合反射率图 (2009年7月31日 03:02:12 BJT)Fig. 5 PPI of S-band radar composite reflectivity at 03:02:12 BJT 31 Jul 2009 |
为了更加全面地比较订正的效果,本文特选择几个区域(如图 3、 4、 5上显示的红色的方框区域,每个区域大小均为12 km×12 km),分析X波段雷达订正前后和S 波段雷达的反射率分布概率和平均值,以验证订正后的效果。通州位于北京市东部,距离X波段雷达21.76 km,距离S波段雷达17.2 km,本文选择通州东北的区域,刚好位于雨区的开始,衰减较小,适合初始对比。统计该区域范围内所有高度层的反射率值,分析其概率分布,如图 6所示,从三者的反射率概率分布趋势上来看,三者的趋势和分布值都相同,都分布在25~35 dBZ 左右,均在30 dBZ出现概率最大值,说明X波段雷达在没有衰减的情况下,和S波段雷达观测是相同的,后面的衰减区域订正后也是可以和S波段雷达进行对比研究的。
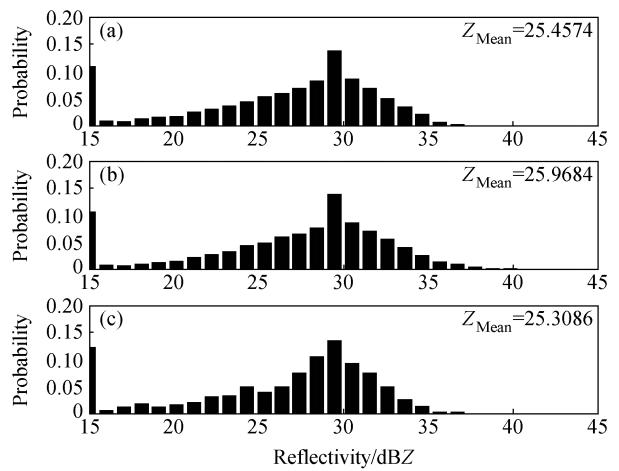 | 图 6 通州东北12 km×12 km区域雷达反射率的概率分布:(a)X波段雷达订正前反射率;(b)X波段雷达订正后反射率;(c)同时段的S波段雷达反射率Fig. 6 Comparison results of probability of radar reflectivity in the northeast of Tongzhou,Beijing(12 km×12 km):(a)Uncorrected ZH of X\|b and radar;(b)Corrected ZH of X\|b and radar;(c)ZH of S\|b and radar observed at the same time |
密云位于北京的西北方向,距离X波段雷达60.55 km,距离S波段雷达71.48 km,对于X波段雷达信号,经过50 km左右的雨区后,电磁波信号存在较 大的衰减,本次选择密云西北12 km×12 km,高度2~4 km的区域作为统计区域。如图 7所示,X波段雷达订正前的反射率值分布在25 dBZ~ 35 dBZ范围内,该区域内的平均值为27.092 dBZ,经过订正后,反射率值分布在27~42 dBZ,平均值为33.8718 dBZ,比订正前平均增加了6.86 dB。与S波段雷达对比,S波段雷达测量值分布在28~40 dBZ,在该区域的平均值为34.248 dBZ。在反射率值的概率分布上,订正后的X波段雷达反射率更加接近S波段雷达,而平均值方面X波段雷达订正后与S波段雷达相差0.3762 dB。
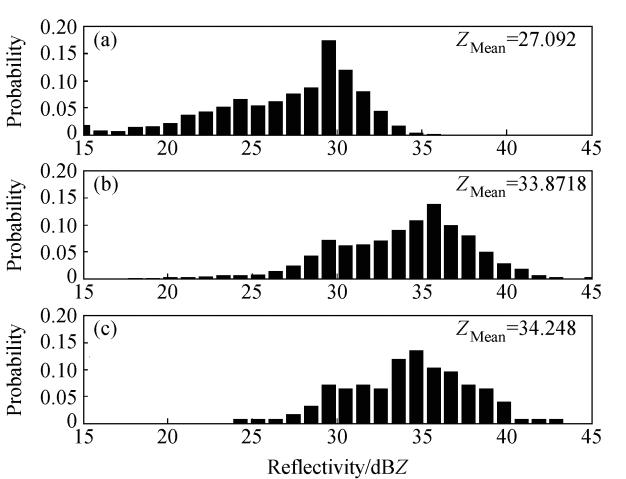 | 图 7 同图 6,但为密云西北12 km×12 km区域、 2 km~4 km高度层Fig. 7 Same as Fig. 6,but for the northwest of Miyun,Beijing(12 km×12 km)in the 2 km-4 km height layer |
除上述两个区域外,另外选了六个区域。各区域所选高度以其距雷达站远近而异,表 2给出八个区域与两部雷达(X波段雷达及S波段雷达)的平均距离及所选高度。
|
|
表 2 八个区域距X波段和S波段雷达站点的距离及统计高度 Table 2 The distances of the eight areas from X and S radars and the selected height |
上述八个区域中,就雨区类型而言,香河、 蓟县区域内为强对流性降雨,反射率在40 dBZ以上,为强对流区; 其他区域反射率值在40 dBZ以下,称之弱对流区。图 8(见文后彩图)给出八个区域X波段订正前后及S波段测得的反射率平均值,由图看出,对平均值在40 dBZ以下的弱对流区域,X波段雷达反射率值订正后有明显提高,且与S波段雷达只相差1 dBZ左右; 强对流区域,X波段订正后反射率值改善更为突出。如香河的反射率平均值订正前为35.39 dBZ,订正后为46.92 dBZ(比订正前高出11.52 dBZ),与S波段雷达的平均值42.44 dBZ更接近,甚至还高出4.48 dB。又如蓟县区域,X波段雷达订正前为20.80 dBZ,订正后达到45.98 dBZ(高出25.18dBZ),更接近S波段雷达反射率值,也高出3.43 dB。
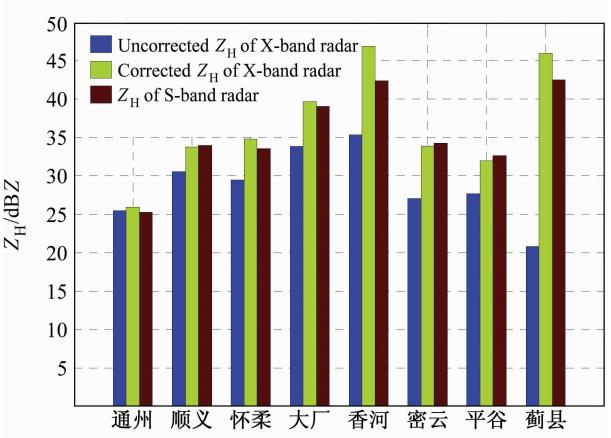 | 图 8 八个具体区域的ZH平均值比较Fig. 8 Comparison results of ZH averaged for the eight areas |
为了进一步分析衰减订正的效果,本文比较了X波段订正前后的KDP~ZH和AH~ZH之间的散点图特性。考虑到个例的特殊性,在30°~90°范围内对流性降雨较少,只有零星的对流区; 在90°~140°范围内,在蓟县—香河—廊坊一带出现一个强对流带,反射率高于40dBZ,因此本文将这次降水过程分为两个区域,对比分析一下强对流性与弱对流性降雨状况下的衰减订正情况。
在弱对流性降雨区域,本文选择方位角30°~90°,仰角为3°、 4°两层数据,距离X波段雷达为30~75 km 范围内的数据。图 9a、 b分别为X波段雷达测得订正前后的KDP~ZH的散点图,图中实线为Park et al.(2005a)通过散射模拟建立的关系式(KDP=αZch)作出的,由图 9a看出,订正前散点图很分散,反射率值分布在20~50 dBZ左右,KDP分布在0~4°/km,很难与Park 的模拟曲线相比较; 订正后,散点图的分布出现了较大变化,图 9b中虚线是由订正后的散点图拟合得到的。可以明显看出,订正后KDP~ZH的拟合曲线与Park曲线基本重合,即订正后的分布与Park 散射模拟的结果相当一致。图 9c、 d分别为订正前后AH~ZH的散点图,其中实线是Park通过散射模拟公式AH=aZbh得到的,虚线是由订正后的散点图拟合出来的曲线。同样地,订正后拟合的曲线与Park的模拟曲线相近,而订正前的误差较大。看来,弱对流性降雨的情况下,订正后与Park的散射模拟结果基本一致这点,从另一角度反映了我们的订正方法的有效性。
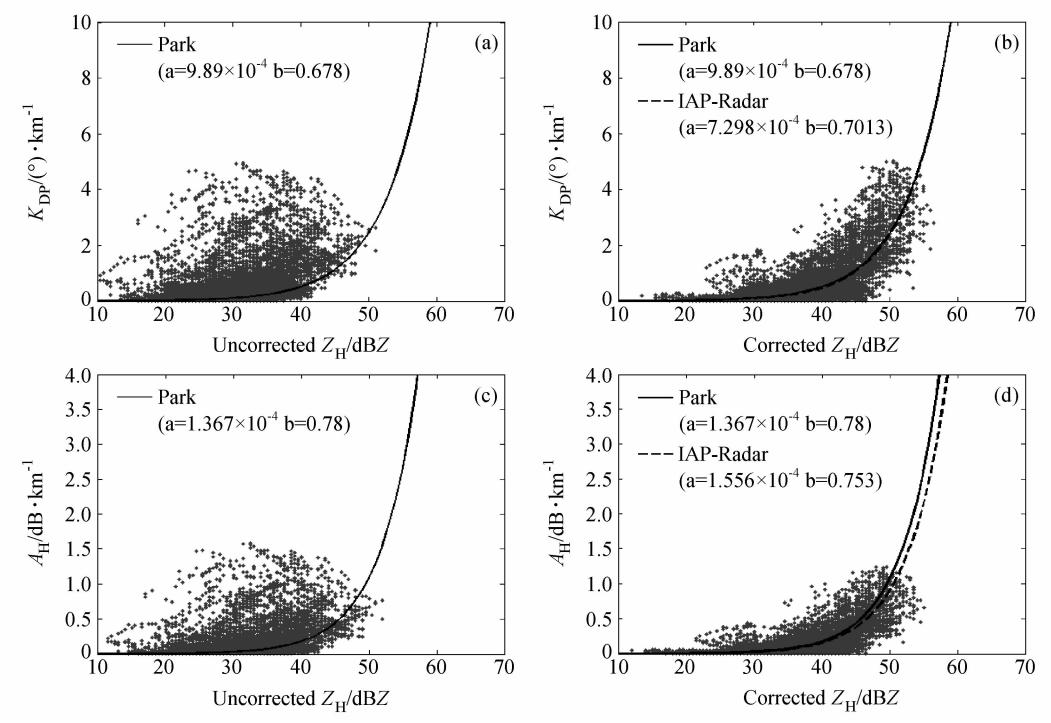 | 图 9 弱对流性降雨情况偏振参数散点图分析Fig. 9 Scatter plots of KDP vs. ZH and AH vs. ZH in the weak convective rain area |
图 10给出蓟县—香河—廊坊一带强对流性降雨区(方位角90°~140°,仰角: 3°、 4°,距X波段雷达距离30~75 km)双偏振参数KDP~ZH和AH~ZH之间的散点图,和弱对流区一样,目的是与Park et al.(2005a)通过散射模拟得到的结果做对比,同样可以看出,订正后较订正前明显得到改善。必须指出的是,在强对流性降雨的情况下,订正效果较弱对流性情况差一些,这可能是在强对流性区域,云内变化比较快,又因粒子直径较大,后向散射相移δ没有完全达到滤除的效果,会对订正效果造成一些影响。
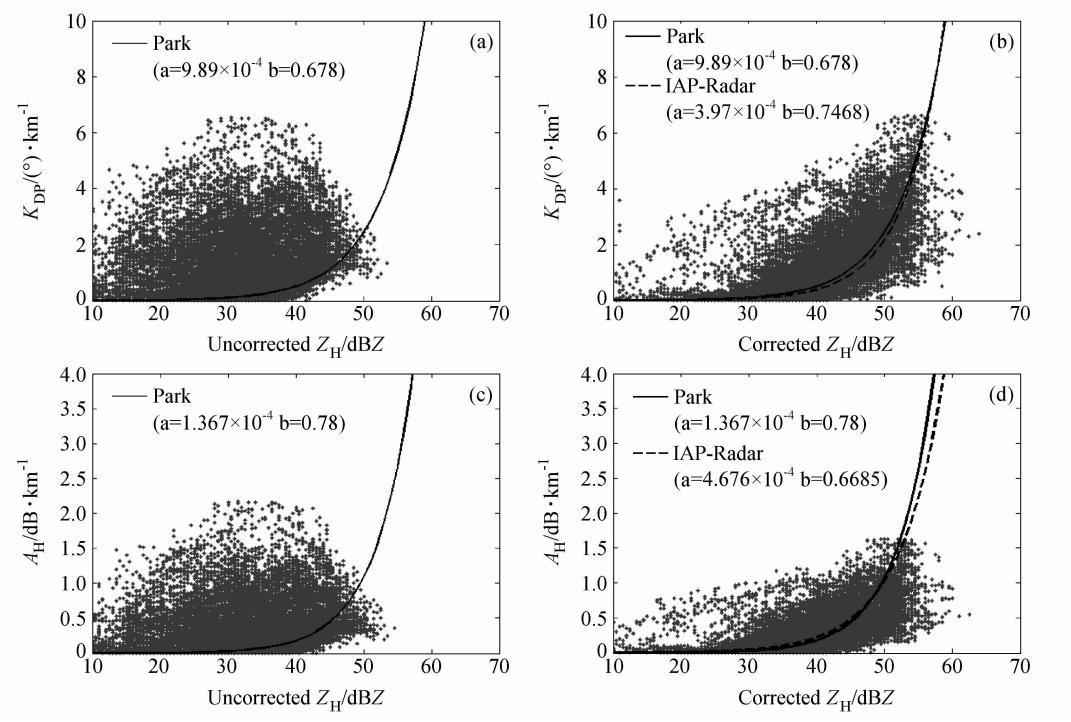 | 图 10 强对流性区域双偏振参数散点图分析Fig. 10 Scatter plots of KDP vs. ZH and AH vs. ZH in the strong convective rain area |
为了进一步验证X波段雷达的订正效果,本文粗略地比较了雷达订正前后的反射率与地面实测的降雨资料。主要选择X波段雷达方位30°~150°范围内的地区。
此次个例的雷达扫描时间为2009年6月8日08:00:01~08:11:46,天线扫描速度为6°/s,用时为11分45秒。本次降雨过程自西南往东北移动,属于系统性层状云降雨。订正前后雷达组合反射率分别如图 11所示,在雷达最佳观测区域30°~150°,10~30 km内,出现环状强反射率区,分析其单层PPI图,系零度层亮带。在30~100 km内,反射率均得到了不同的加强。图 12给出相对应的12分钟内(08:00:00~08:12:00)的降雨资料。在订正前,在顺义东部、 平谷区和密云区域反射率值均较小,经过订正后,反射率得到了加强,达到了30~40 dBZ,而本区域内的降雨资料显示,这些区域的12分钟降雨量分布在1~5 mm左右,在通州东南部,反射率也加强到35~45 dBZ,该区域的降雨量达到1.5~5 mm。总之,经过订正后的X波段雷达组合反射率分布与地面降雨分布相似性更高。
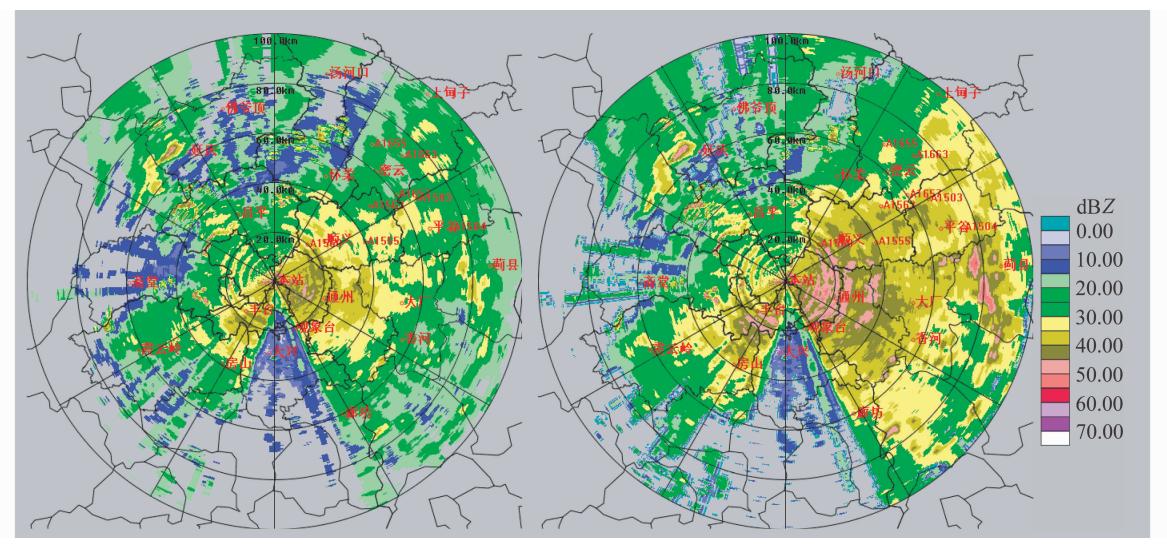 | 图 11 订正前后雷达组合反射率图(2009年6月8日08:00~08:12 BJT)Fig. 11 Composite reflectivity of X\|b and radar before correction(left) and after correction(right)during 0800-0812 BJT 8 Jun 2009 |
为了定量地了解订正前后反射率值与地面降雨量的关系,根据降雨量分布选取几个地面雨量站,分析该站点上空订正前后雷达反射率的变化。选择站点位置如图 12所示,订正前后反射率值如图 13所示,X轴代表各个站点信息,其排列顺序据雷达的远近而定。图 13采用双坐标系,左面的纵坐标代表反射率值大小,实线和虚线分别代表订正前后反射率值,右边的纵坐标代表雨强值,点虚线代表这些站点的实测雨强值。我们可以看到,距离雷达的越远,反射率越大,衰减越严重,反射率订正前后的差别越大,订正后反射率值与地面雨强分布存在较高的一致性。为了更具体地了解订正的效果,我们用订正前后的雷达资料反演了几个地面站的雨强,用于与实测降水强度作对比,如图 14所示,点虚线(R)为地面实测雨强,虚线和实线分别为订正前后雷达反射率值反演的雨强,反演公式为: R=0.02462×100.07305ZH(其中R的单位是mm/h,ZH单位为dBZ),此公式是我们利用本雷达数据和北京地区地面实测降雨资料,拟合得出的适合北京地区降雨估计的经验公式。可以看出,在这些站点上,用订正后雷达反射率反演的雨强比订正前更接近实测的地面雨强,进一步验证了这一订正方法的效果。
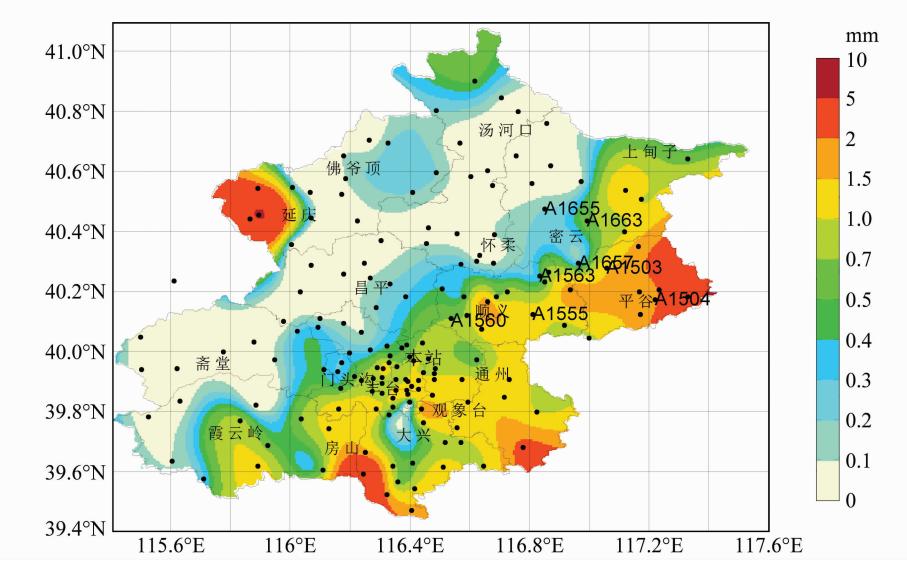 | 图 12 地面测量降雨量图(2009年6月8日08:00~08:12 BJT)Fig. 12 Rainfall distribution from surface rain\|gauge observation during 0800-0812 BJT 8 Jun 2009 |
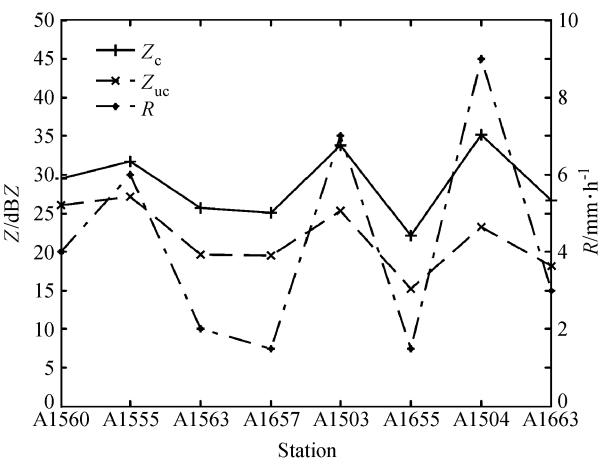 | 图 13 选择站点上订正前后雷达反射率与雨强值(2009年6月8日08:00~08:12)Fig. 13 Corrected and uncorrected radar reflectivity(Zc,Zuc) and observed rainfall rate at selected rain gauge stations(0800\|0812 BJT 8 Jun 2009) |
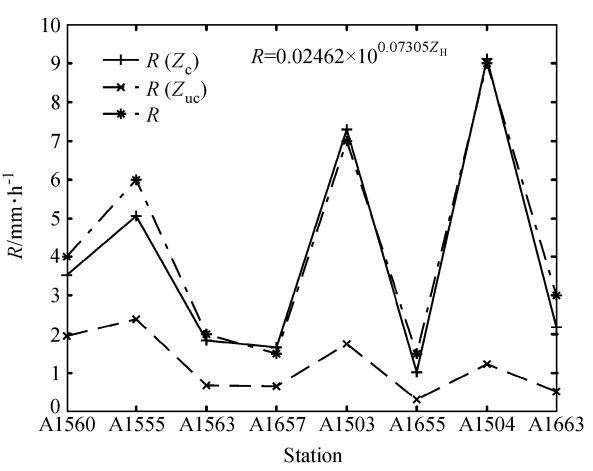 | 图 14 选择站点上订正前后雷达反演雨强与实测雨强对比(2009年6月8日08:00~08:12)Fig. 14 Comparison of rain gauge\|observed(R) and retrieved(R(Zc),R(Zuc))rainfall rates at selected rain\|gauge stations(0800\|0812 BJT 8 Jun 2009) |
本文主要给出X波段双偏振雷达反射率衰减订正的一种方法,方法要点及验证分析归纳如下:
(1)订正前资料的预处理: 本文数据质量控制和预处理工作中,运用低通FIR滤波器,消除了高频噪声,减弱后向散射相移δ的影响,达到了差分传播相移ΦDP(r)平滑处理。
(2)订正方法: 本文使用自适应约束算法对反射率进行衰减订正,这种方法利用雷达资料本身,综合考虑了雨滴谱、 粒子形状、 温度等因素的影响,对于每一个不同α值,计算该雨区AH并重构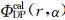 ,将
,将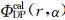 与雷达测量的ΦDP(r)相比,以其差值最小作为约束条件,不断调整得到每一帧雷达数据订正的最佳系数,进行ZH的衰减订正。该方法能有效准确计算出衰减率,达到反射率的订正。
与雷达测量的ΦDP(r)相比,以其差值最小作为约束条件,不断调整得到每一帧雷达数据订正的最佳系数,进行ZH的衰减订正。该方法能有效准确计算出衰减率,达到反射率的订正。
(3)衰减订正方法的效果验证:
① 将X波段双偏振雷达订正前后与同时段S波段雷达反射率进行对比,看出订正后的反射率值与S波段雷达有较高的一致性; 详细对比了一些特定区域中反射率的概率分布和均值发现,订正后的X波段雷达反射率在分布趋势和均值均与S波段雷达有较好的一致性; 反射率在40 dBZ以下,X波段雷达和S波段雷达基本一致,误差在1 dB左右,但在40 dBZ以上,订正值比S波段雷达高2~4 dB。
② 分析订正前后X波段双偏振雷达参数KDP~ ZH和AH~ZH之间的散点图,并拟合订正后的KDP~ZH和AH~ZH经验公式的系数表明,订正后的散点图较订正前与偏振参数间的经验公式的一致性更好,并且本文拟合的结果通过散射模拟得到的结果基本上是一致的。根据分析不同类型的降雨区域发现,弱对流性降雨的订正效果比对流性降雨好。
③ 与地面实测降雨资料进行对比,分析对比X波段雷达订正前后反射率分布与地面实测降雨分布后,发现订正后较订正前,无论在降雨的范围、 分布和强度上,两者的一致性好得多,也说明了该订正方法的有效性。
总体上看,通过本文所述的预处理和订正方法,X波段偏振雷达在估测降水中的强衰减问题可以得到明显的改善。
| [1] | Anagnostou E N, Grecu M, Anagnostou M N. 2006. X-band polarimetric radar rainfall measurements in keys area microphysics project [J]. J. Atmos. Sci., 63 (1): 187-203. |
| [2] | Bringi V N, Chandrasekar V, Balakrishnan N, et al. 1990. An examination of propagation effects in rainfall on radar measurements at microwave frequencies [J]. J. Atmos. Oceanic Technol., 7 (6): 829-840. |
| [3] | Bringi V N, Keenan T D, Chandrasekar V. 2001. Correcting C-band radar reflectivity and differential reflectivity data for rain attenuation: a self-consistent method with constraints [J]. IEEE Transactions on Geoscience and Remote Sensing, 39 (9): 1906-1915. |
| [4] | Carey L D, Rutledge S A, Ahijevych D A, et al. 2000. Correcting propagation effects in C-band polarimetric radar observations of tropical convection using differential propagation phase [J]. J. Appl. Meteor., 39 (9): 1405-1433. |
| [5] | Chandrasekar V, Lim S, Gorgucci E. 2006. Simulation of X-band rainfall observations from S-band radar data [J]. J. Atmos. Oceanic Technol., 23 (9): 1195-1205. |
| [6] | Delrieu G, Andrieu H, Creutin J D. 2000. Quantification of path-integrated attenuation for X- and C-band weather radar systems operating in Mediterranean heavy rainfall [J]. J. Appl. Meteor., 39 (6): 840-850. |
| [7] | 段树, 张凌, 刘锦丽, 等. 2002. 双线偏振双波段 (X/Ka) 主被动微波遥感系统的研制与初步试验 [J]. 遥感学报, 6 (4): 289-293.Duan Shu, Zhang Ling, Liu Jinli, et al. 2009. Development of an active and passive dual-wavelength (X/Ka) dual-polarization remote sensing system and its preliminary test [J]. Journal of Remote Sensing (in Chinese), 6 (4): 289-293. |
| [8] | Gorgucci E, Chandrasekar V. 2005. Evaluation of attenuation correction methodology for dual-polarization radars: application to X-band systems [J]. J. Atmos. Oceanic Technol., 22 (8): 1195-1206. |
| [9] | Gorgucci E, Chandrasekar V, Baldini L. 2006. Correction of X-band radar observation for propagation effects based on the self-consistency principle [J]. J. Atmos. Oceanic Technol., 23 (12): 1668-1681. |
| [10] | 何宇翔. 2009. 水凝物粒子双线极化雷达后向散射和衰减特性分析与应用研究 . 中国科学院大气物理研究所博士士学位论文, 80pp. He Yuxiang. 2003. Dual-polarization Radar Backscattering and Attenuation Characteristic of Hydrometeor Analysis and Application Research . Ph. D. dissertation (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Sciences, 80PP. |
| [11] | 何宇翔, 吕达仁, 肖辉, 等. 2009. X波段双线极化雷达反射率的衰减订正 [J]. 大气科学, 33 (5): 1027-1037.He Yuxiang, Lü Daren, Xiao Hui, et al. 2009. Attenuation correction of reflectivity for X-band dual polarization radar [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 33 (5): 1027-1037. |
| [12] | Hitschfeld W, Bordan J. 1954. Errors inherent in the radar measurement of rainfall at attenuating wavelengths [J]. J. Atmos. Sci., 11 (1): 58-67. |
| [13] | 胡志群, 刘黎平, 楚荣忠. 2008. X波段双线偏振雷达不同衰减订正方法对比及其对降水估测影响研究 [J]. 气象学报, 66 (2): 251-261.Hu Zhiqun, Liu Liping, Chu Rongzhong. 2008. Comparison of different attenuation correction methods and their effects on estimated rainfall using X-band dual linear polarimetric radar [J]. Acta Meteorologica Sinica (in Chinese), 66 (2): 251-261. |
| [14] | Hubbert J, Bringi V N. 1995. An iterative filtering technique for the analysis of copolar differential phase and dual-frequency radar measurements [J]. J. Atmos. Oceanic Technol., 12 (3): 643-648. |
| [15] | Hubbert J, Chandrasekar V, Bringi V N, et al. 1993. Processing and interpretation of coherent dual-polarized radar measurements [J]. J. Atmos. Oceanic Technol., 10 (2): 155-164. |
| [16] | Jameson A R. 1992. The effect of temperature on attenuation-correction schemes in rain using polarization propagation differential phase shift [J]. J. Appl. Meteor., 31 (9): 1106-1118. |
| [17] | Le Bouar E, Testud J, Keenan T D, et al. 2001. Validation of the rain profiling algorithm "ZPHI" from the C-band polarimetric weather radar in Darwin [J]. J. Atmos. Oceanic Technol., 18 (11): 1819-1837. |
| [18] | Matrosov S Y, Cifelli R, Kennedy P C, et al. 2006. A comparative study of rainfall retrievals based on specific differential phase shifts at X- and S-band radar frequencies [J]. J. Atmos. Oceanic Technol., 23 (7): 952-963. |
| [19] | Park S G, Bringi V N, Chandrasekar V, et al. 2005a. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band. Part I: Theoretical and empirical basis [J]. J. Atmos. Oceanic Technol., 22 (11): 1621-1632. |
| [20] | Park S G, Maki M, Iwanami K, et al. 2005b. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band. Part II: Evaluation and application [J]. J. Atmos. Oceanic Technol., 22 (11): 1633-1655. |
| [21] | Ryzhkov A, Zrni D S. 1995. Precipitation and attenuation measurements at a 10-cm wavelength [J]. J. Appl. Meteor., 34 (10): 2121-2134. |
| [22] | Smyth T J, Illingworth A J. 1998. Correction for attenuation of radar reflectivity using polarization data [J]. Quart. J. Roy. Meteor. Soc., 124 (551): 2393-2415. |
| [23] | Testud J, Le Bouar E, Obligis E, et al. 2000. The rain profiling algorithm applied to polarimetric weather radar [J]. J. Atmos. Oceanic Technol., 17 (3): 332-356. |
| [24] | Zrni D S, Ryzhkov A. 1996. Advantages of rain measurements using specific differential phase [J].J. Atmos. Oceanic Technol., 13 (2): 454-464. |
 2012, Vol. 36
2012, Vol. 36

