2. 中国气象局干部培训学院, 北京 100081
2. China Meteorological Administration Training Center, Beijing 100081
自从Tapp and White(1976)提出完全弹性非静力模式(NH)以来,经过约30多年的努力,现在世界上的气象中心已建立的业务或准业务模式已不下10个,其积分范围大多是有限区域,少数既是全球又含有有限区域(廖洞贤,2004)。Steppler et al.(2003)、 Steppler(1995)和Dudhia(1995)认为: 垂直坐标的选择、 无摆动且计算精确的平流格式的构造和椭圆型方程的数值解的收敛速度应给予特别关注,其中第一个问题在采用高分辨率时因陡峭地形使坐标面倾斜会引起计算不稳定。不过,所谈内容仅限于计算方法,对于动力方面的问题还未涉及。
关于动力方面的问题,早期Tapp and White(1976)以及张可苏和周晓平(1980)在静力近似和完全弹性非静力情况下,比较了高频、 小振幅的重力惯性波的性质,结论是: 在静力情况下会引起虚假的高频重力波,应采用非静力方法。2002年,Yeh et al.(2002)还发现: 由于静力近似略去了dw/dt,非静力导致的内波崩溃和翻转作用当水平运动尺度在10 km以下时,不可忽视。但这些研究还限于较窄的范围,还没有进行一般性研究和能量分析。
近年来,一些气象中心企图用非静力模式制作全球中长期预报和气候预测,如UKNC(Cullen et al 1997)、 GEM(Cote et al., 1998)和GRAPES(薛纪善等,2008)(缩写词全称见附录,下面其他缩写词全称亦然)。它们的预报效果表明: 与采用同样分辨率的静力原始方程模式(全球谱模式或差分模式)相比,目前还看不出有明显的优势(Yeh et al,2002)。另外,用GRAPES模式计算的垂直速度有时会异常大,引起虚假的格点暴雨。WRF模式也反映有类似问题(Skamarock et al., 2005),WRF曾用约束Courant数以达到约束垂直速度的nudging方法。
不论对于静力模式或非静力模式,能量守恒和能量转换都应是模式设计中需要考虑的。对此,很多人都进行过研究,特别是对于前一种模式。由于这类模式发展的时间较长,结果比较成熟,可以作为后一类模式设计的参考。早在20世纪60年代,Arakawa(1966)就提出过正压过滤模式长期预报积分的方案,以后,Arakawa and Lamb(1977)、 Arakawa and Suartz(1983)又研究UCLA大气环流模式的保持能量守恒的数值方案和sigma坐标系中原始方程模式的垂直差分方案,其结果多次为数值预报模式设计者所引用。但是,Arakawa等的方案只能在时间连续,空间离散情况下保持能量守恒(即瞬时能量守恒),这是其不足之处。对于这个问题,曾庆存和张学洪(1987)以及左瑞亭等(2004)曾提出时空差分的能量守恒的隐式方案。1995年,季仲贞等(1995)提出时空差分的能量守恒的显式方案。至于完全弹性非静力模式,由于问题比较复杂,研究能量守恒的较少。研究方案有针对有限区模式垂直差分的Taylor(1984)方案和针对有限区模式的Gallus and Rancic(1996)方案,以及致力于全球气候模式的Satoh(2002)方案。Satoh以连续方程、 动量方程和全能量方程构成模式的动力方案,计算结果令人鼓舞,其质量守恒和总能量守恒的计算都在舍入误差精度以内。
根据上面的分析和提出的问题,下面我们将作进一步的分析并对某些问题提出解决的方法。全文共6节,第2到第6节依次是: 对垂直运动方程进行尺度分析的结果和垂直扰动运动方程各项量级接近的可能、 垂直扰动气压梯度力的截断误差、 多级扰动法、 多级扰动的性质和结论。
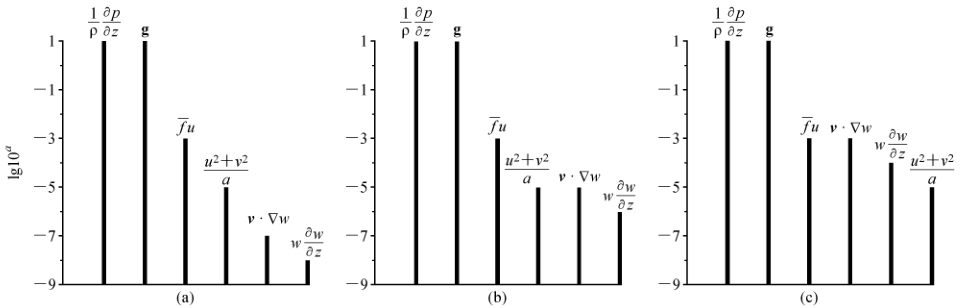 |
图 1 大气垂直运动方程中各项的量级(倾向量级和v · Δ w量级相同):(a)L=106 m;(b)L=105 m;(c)L=104m Fig.1 Order of magnitude of each term in the vertical equation of motion for three kinds of horizontal motion(the magnitude of the tendency term is the same as that of v · Δ w):(a)L=106 m;(b)L=105 m;(c)L=104 m |
根据廖洞贤(2008)研究中的尺度分析结果,我们可以把在绝热无耗散情况下大气垂直运动方程各项的量级表示出来(图 1)。图 1中纵坐标是lg10a,10a是量级,横坐标是方程各项。从图 1可以看出如下几个特点:
(1)不论对于水平尺度L=106 m、 L=105 m或L=104 m的运动,最大项都是垂直气压梯度力项(VPGF)和重力项(G),而最小项却各有不同,对于L=106m和L=105m的运动,是随L的减小而增大的垂直平流项(VAD); 对于L=104m的运动,是曲率项(CUR)。由于VPGF、 G和CUR不随L而变,VPGF 与CUR之差也不随L而变,故对于这三种水平尺度的运动,最大项和最小项之间的量级差(以下简称最大量级差)总是随L的减小而减小的。根据图 1所示,对于L=106m、 L=105 m 或L=104 m的运动,最大量级差依次是9个、 7个和6个量级。
(2)最大项和次大项之间差4个量级。根据廖洞贤(2008)的研究,VPGF和最小项之间的量级差最大,应取的垂直分辨率最高,而对于一定的L,带有垂直差商项的量级愈大,其截断误差的量级也愈大。因此,通过分离技术使VPGF相应扰动项的量级减小,会使所需垂直分辨率降低,而在同样分辨率下,用分离技术时的截断误差比未用时的截断误差显著减小。在已设计的完全弹性非静力模式中,Tapp and White(1976)、 Dudhia(1993)、 Bubnova et al(1995)、 Xue et al.(2000)和薛纪善等(2008)的模式,毫无例外地都采用只随高度而变的气候值作基本态变量,并用来对随时空而变的热力学变量进行分离,用对后者的扰动作预报。看来这样做有一定好处。为了了解这种好处,廖洞贤和孙岚(2003)曾用19种地面温度(Ts)和温度的垂直递减率(Γ)的组合构成的温度廓线和用气候值且只是z的函数的基本态廓线所作的计算,扰动项的量级比VPGF和G仅降低约1~2个量级,还不足以使方程达到各项量级接近的程度。但是,也应看到如果我们用类似方法对扰动进行分离,则有可能使更高一级扰动项的量级继续降低,经过几次使方程达到各项量级接近,使与最大量级差相应的垂直分辨率达到可用的程度。当然,这些想法还须分析论证。
3 垂直扰动气压梯度力项的截断误差3.1 离散的垂直扰动运动方程和其各项的量级
设δF/δz=əF/əz+E(δF/δz),其中E(δF/δz)是δF/δz的截断误差。以L=106 m的运动为例,我们可以把离散的大气垂直扰动运动方程写成:
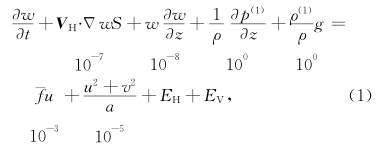
在方程(1)中,除被离散项外,如果不计观测、 分析或舍入误差的影响,其他项都是可以精确计算的。这样,在第1节中提到的 w异常增大应该是dw/dt或əw/ət出现异常造成的,而dw/dt或əw/ət出现异常只可能是方程中出现很大 E(VPP-GF)所致。如果E(VPPGF)是VPPGF的1/100,则E(VPPGF)的量级是10-2。于是,E(VPPGF)的量级就大于fu、(u2+v2)/a和平流项的量级。
3.3 对E(VPPGF)的估计 为了得到具体的结果,我们还须对E(VPP-GF)进行估计。 取T和静止大气基本态变量 各是
各是
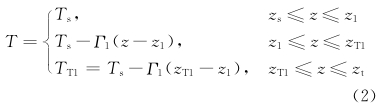

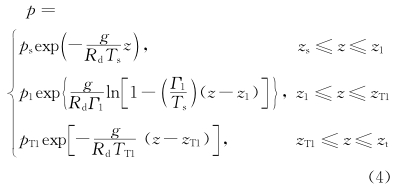
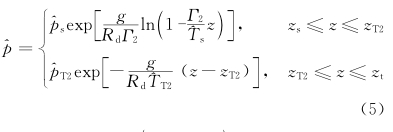
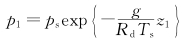 ,是气压在z1处的值; 同样,pT1和
,是气压在z1处的值; 同样,pT1和 分别表示在zT1处的气压和在zT2处的基本态气压。这样,我们可以求出p(1),ρ(1)。至于E(VPPGF),在取中心差的情形,利用Taylor展开可以得到
分别表示在zT1处的气压和在zT2处的基本态气压。这样,我们可以求出p(1),ρ(1)。至于E(VPPGF),在取中心差的情形,利用Taylor展开可以得到
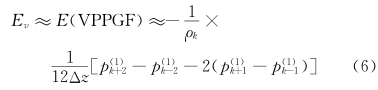
| 表 1 取3种Δz得到的|E(VPPGF)| * Table 1 |E(VPPGF)| corresponding to three different Δz |
比较Δz=1000 m时的|E(VPPGF)|和方程(1)中各项的量级,可以看出: 除VPPGF和浮力项(BUOY)外,它比所有的项都大。这样,əw/ət 受到E(VPPGF)的影响就掩盖了fu,(u2+v2)/a和平流项等对əw/ət 的贡献。而且,由于VPPGF总是方程中的最大项,这种现象还会持续存在; 虽然(u2+v2)/a总为正,fu在北半球西风带中基本为正,它们的持续作用仍不容易表现出来。这是不合理的。
3.4 垂直分辨率的问题从前面的分析讨论来看,E(VPPGF)所以不合理,是选取垂直分辨率不当造成的。其实并不尽然。从表 1可以看到: 提高垂直分辨率可以使E(VPPGF)减小,但是,取到Δz=20 m仍有5.0384×10-6 m/s2的误差; 对于L=106 m的运动,对əw/ət的影响仍大于水平和垂直平流项对əw/ət 的贡献。 看来要彻底避免这种现象的出现,只有再提高分辨率才行。不过,根据朱禾等(2007),要避免这种现象,Δz须取为
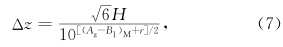
4 多级扰动法 4.1 多级扰动的构造
根据方程(1),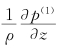 和
和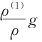 是其最大项。在这个条件下,我们可以得到如下结果:
是其最大项。在这个条件下,我们可以得到如下结果:
结果1 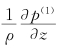 和
和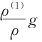 量级相等符号相反。
量级相等符号相反。
因为,如二者量级不相等,则其中必有一项的量级大于另一项,这样方程中最大项只有一项,这就违反了尺度分析中一个方程的最大项至少有2项的结论(叶笃正等,1988; 刘式适和刘适达,1991); 另外,如它们的符号相同,则方程不能达到平衡,故结果1成立。
根据结果1,我们可以构造1级扰动平衡方程
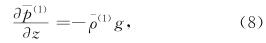
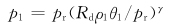
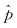 +p(1),ρ1=
+p(1),ρ1=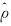 +ρ(1),θ1=
+ρ(1),θ1=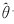 +θ(1),pr是参考气压,取为常数。
+θ(1),pr是参考气压,取为常数。
方程(8)推广,设
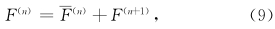
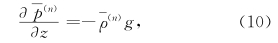
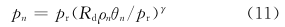
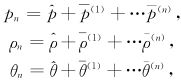
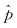 ,ρ0=
,ρ0=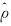 ,θ0=
,θ0=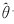 。
。
而F(n+1)表示F(n)对F(n)的扰动,如取

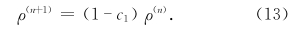
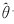 、0(1),直到0(n-1)已知,还可以求出0(n),从而,从ρ(n)、 θ(n)、 p(n)通过(9)求出ρ(n+1)、 θ(n+1)、 p(n+1)。不过,在工作中还可以利用一些近似式来达到目的。在下节中我们将进行推导。
4.2 一些近似关系
、0(1),直到0(n-1)已知,还可以求出0(n),从而,从ρ(n)、 θ(n)、 p(n)通过(9)求出ρ(n+1)、 θ(n+1)、 p(n+1)。不过,在工作中还可以利用一些近似式来达到目的。在下节中我们将进行推导。
4.2 一些近似关系对状态方程
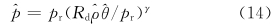

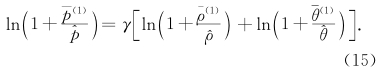
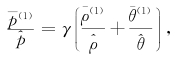
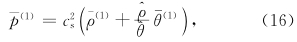
 。类似地,用p、 ρ、 θ代替方程(11)中的pn、 ρn、 θn利用p、
。类似地,用p、 ρ、 θ代替方程(11)中的pn、 ρn、 θn利用p、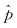 、 p(1)等的关系,我们还有
、 p(1)等的关系,我们还有 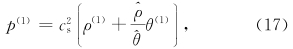
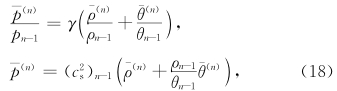
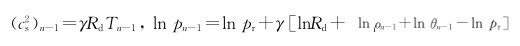 。如p=pn+p(n+1),ρ=ρn+ρ(n+1),θ=θn+θ(n+1),还有
。如p=pn+p(n+1),ρ=ρn+ρ(n+1),θ=θn+θ(n+1),还有 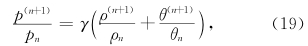
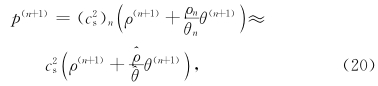
用ρ乘方程(1),得到
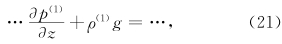
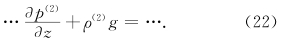
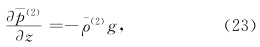
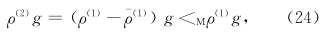
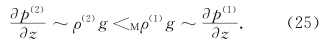
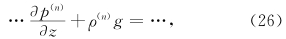
结果2 əp(n)/əz和ρ(n)g量级相等,符号相反。
于是,利用推导不等式(24)和(25)同样的方法,可以得到
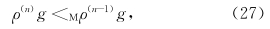

为了说明多级扰动法的作用,我们利用扰动项量级随n减小的性质来估计E(VPPGF)。用n代替式(6)中的1,用3.3节中的理想场,按式(9)、(10)、(12)、(13)和附录中解n级扰动平衡方程的方法,仍取表 1中的分辨率,可以求出|E(VPPGF)|,结果如图 2所示。从图 2可见,|E(VPPGF)| 的量级随Δz的减小而减小,也随n的增加而减小,都可以使E(VPPGF)对倾向的影响减小。容易看出: 不论取c1=0.91或0.95,当n=3,Δz=200 m时,|E(VPPGF)| 都小于10-5,|E(VPPGF)| 对倾向的影响已不致歪曲或掩盖fu和(u2+v2)/a对倾向的贡献了。
 |
图 2 |E(VPPGF)| 的计算结果。纵坐标是lg|E(VPPGF)|(|E(VPPGF)| 以10a表示) Fig.2 Results of |E(VPPGF)| . The ordinate represents lg|E(VPPGF)|(shown as lg10a) |
如果n增加1,扰动项减小一个量级,则扰动项ρ(1)g/ρ减小到和u的量级相等时,fn=n1,这时VPPGF减小了3个量级。按式(7)用2阶中心差应取的Δz如表 2所示。如果认为Δz大于100 m为可用,则从表 2可见,除L=106 m的运动外,对于L=105 m和L=104 m的运动,Δz可用。
| 表 2 VPPGF和BOUY减小3个量级后应取的 Δz Table 2 Δz after both VPPGF and BOUY having decreased by 3 orders of magnitude |
至于L=106 m的运动,如我们只要求E(VPPGF)的量级小于曲率项,则VPPGF和BOUY只减小2个量级,(Az-B1)M为3,按式(7),Δz= 245 m,也是可用的。
5 多级扰动的性质 5.1 2 个关于 Δ(=p(1)/z+ρ(1)g)的结果
结果3 利用式(9)和方程(10)有
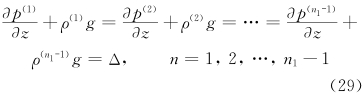
结果4 设有满足静力方程的变量p1、 ρ1和p2、 ρ2,则它们的差p′(=p1-p2)和ρ′(=ρ1-ρ2)必满足式
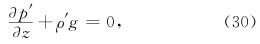

显然扰动平衡方程中的气压扰动 (n)是静力扰动。以n级扰动平衡方程
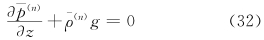
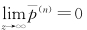 的条件下(证明见5.3节),可以得到
的条件下(证明见5.3节),可以得到
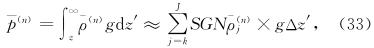
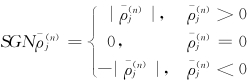
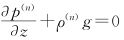 的解p(n)也是静力扰动。
的解p(n)也是静力扰动。
5.2.2 多级扰动静力扣除法
多级扰动法实质上是多次利用扰动平衡方程的解,从p(n)中扣除其所含大小与p(n)相同的静力扰动部分,使p(n)量级减小,达到əp(n)/əz与其它项量级接近的一种方法。这种方法也可以称作 “多级扰动静力扣除法”。
5.2.3 修正的大气基本态变量
从大气总的来看,因为ρ=ρn+ρ(n+1),p=pn+p(n+1),易证əpn/əz=-ρng,故ρn、 pn各可代替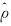 和
和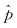 作为大气修正的基本态变量,ρ(n+1)和p(n+1)各代替ρ(1)和p(1)作为ρ、 p和ρn和pn之间的扰动。这种基本态变量虽然不一定是z的函数而是时间和空间的函数,但因ρ(n+1)=(1-c1)nρ(1),p(n+1)=(1-c1)np(1)使ρ(n+1)ρ(1),p(n+1)p(1),当n≥1时,这种代替使ρn、 pn大气垂直廓线和ρ、 p大气垂直廓线或实际大气垂直廓线达到很接近的程度; 而且,每次修正都是通过静力平衡达到的,可以认为: 模式大气的绝大部分已不含有垂直声波。不过,由于(u2+v2)/a,u和dw/dt的存在,它们还会引起非静力扰动,从而,使这种作用降低。不过,非静力扰动一般远比静力扰动为小,其所起的作用一般不太明显。只是,这时仍存在水平声波,考虑计算稳定性问题,应当把它作为主要的抑制对象。下面我们用一个例子来说明。
作为大气修正的基本态变量,ρ(n+1)和p(n+1)各代替ρ(1)和p(1)作为ρ、 p和ρn和pn之间的扰动。这种基本态变量虽然不一定是z的函数而是时间和空间的函数,但因ρ(n+1)=(1-c1)nρ(1),p(n+1)=(1-c1)np(1)使ρ(n+1)ρ(1),p(n+1)p(1),当n≥1时,这种代替使ρn、 pn大气垂直廓线和ρ、 p大气垂直廓线或实际大气垂直廓线达到很接近的程度; 而且,每次修正都是通过静力平衡达到的,可以认为: 模式大气的绝大部分已不含有垂直声波。不过,由于(u2+v2)/a,u和dw/dt的存在,它们还会引起非静力扰动,从而,使这种作用降低。不过,非静力扰动一般远比静力扰动为小,其所起的作用一般不太明显。只是,这时仍存在水平声波,考虑计算稳定性问题,应当把它作为主要的抑制对象。下面我们用一个例子来说明。
5.2.4 实例计算
为了说明修正的大气基本态变量垂直廓线和实际大气变量垂直廓线当n≥1时相接近的程度,我们把NCEP的2003年7月31日1800 UTC在(30°N,120°E)从1000 hPa~10 hPa的等压面温度资料,通过线性插值转换为z坐标的以200 m为Δz的格点值T,p按Lorentz网格依次放置在整数层和半数层上。还采用3.3节用理想场计算的z坐标格点的和,用前面的方法算出ρn和pn,从而算出ρ-ρn和p-pn。但这时除ρ-ρn是迅速随n减小外,p-pn从n=0到1减小得很快,而从n=1到3则随n有所增加,增加值占从n=0到1减小值的15.8%(图略)。其所以如此,显然和计算中求z坐标p、 ρ值时采用的线性插值有关,因为这种插值不一定满足静力平衡条件,即使用原NCEP温度资料得出的ρ、 p格点值满足该条件。由于这样,我们不能用公式p(n)=(1-c1)n-1p(1)来估计p-pn,而只能用4.1节中pn的表示式计算,这样,在p-pn中不仅含有插值误差,还含有因计算 (1)等引入的数值积分的误差,这比ρ-ρn中所含的误差还多。为了这个缘故,我们改变了计算方案: 只对ρ插值,而p则用静力方程求出,并令其他方法不变,和也不变。这样得到的ρ-ρn和p-pn的结果各表示在图 3和图 4中。从这两幅图中可以看出: ρ-ρn和p-pn都随n减小,只是当n从0到1时减小得很快,而1到3时,减小的幅度较小罢了。这说明: 修正的大气基本态变量垂直廓线和实际大气变量垂直廓线是随n的增加而接近的。注意: 为了使单位协调,ρ采用hPa · s2 · m-2,p采用hPa(Stull,1988)。
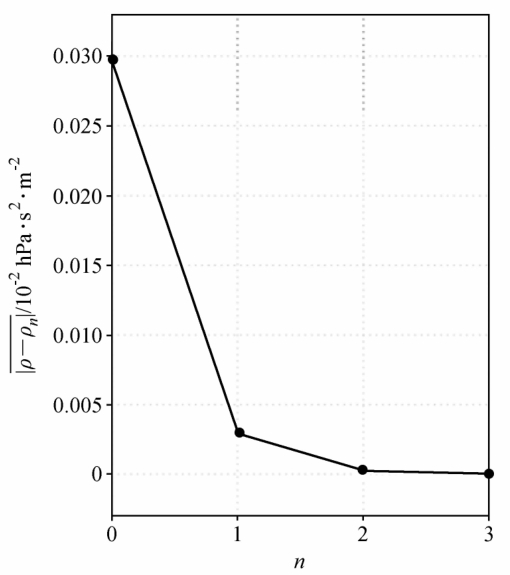 |
图 3 |ρ-ρn|随n的变化 Fig.3 Variation of |ρ-ρn| with n |
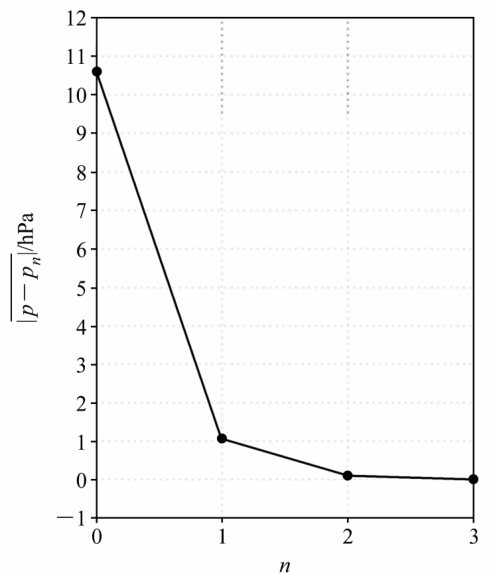 |
图 4 |p-pn| 随n的变化 Fig.4 Variation of |p-pn| with n |
凡形式上不满足形如方程(32)的扰动都是非静力扰动。如
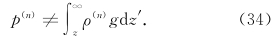
为了方便,我们不妨把式(32)改写成

并令p(n)=p(n)H+p(n)N,其中下标H,N各表示静力变量和非静力变量; S(n)是z的函数; 且
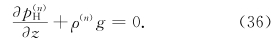
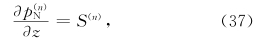
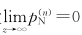 ,则
,则 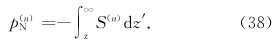
设p,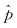 和ρ,
和ρ,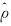 均各满足5.1节中结果4和Δ=0的条件,则可以推出如下结果。
均各满足5.1节中结果4和Δ=0的条件,则可以推出如下结果。
结果5 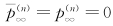 。其中
。其中 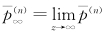 ;
; 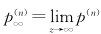 。证明如下。先证n=1的情形。这时
。证明如下。先证n=1的情形。这时
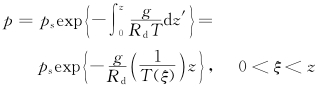

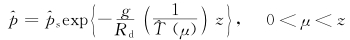

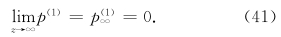
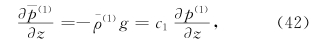

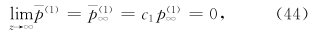

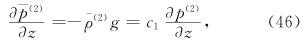

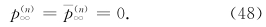
结果6  。证明如下。对方程(42)作从zt到∞处的积分,利用式(44),有
。证明如下。对方程(42)作从zt到∞处的积分,利用式(44),有
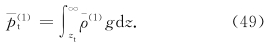
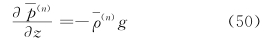
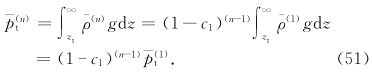
从前面的讨论,可以得出以下初步结论:
(1)用多级扰动法可以使大气垂直扰动运动方程中量级最大的垂直扰动气压梯度力项和浮力项的量级随级次减小,使方程中最大的截断误差对倾向的影响不致歪曲或掩盖较小的垂直科氏力项和曲率项对倾向的贡献,从而使倾向计算合理,可以避免w出现异常增大的现象; 而具有持续作用的垂直科氏力项和曲率项的作用也可以得到充分发挥,有利于制作较长时期的天气预报。
(2)扰动平衡方程的解表示静力扰动。多级扰动法实质上是多次利用不同级次的静力扰动扣除原扰动中和p(n)大小相同的静力部分,达到扰动方程中各项量级接近的一种方法。而且,从大气总的情况来看,经过这法不多几次修正,大气基本态ρn,pn垂直廓线的绝大部分和实际大气ρ,p垂直廓线已很接近,可以认为,通过静力平衡,模式大气基本上已不含有垂直声波; 抑制快波使计算稳定的主要对象应是水平声波。
(3)可以证明: 在应用多级扰动法时,尽管级次n可以变化,但与对流活动密切有关的Δ(=əp(n)/əz+ρ(n)g)却不随n而变,因各级扰动垂直运动方程中其他项均不随n而变,故n的变化不改变原扰动方程的性质。
附录 1 n 级扰动平衡方程的数值解n级扰动平衡方程可以写成
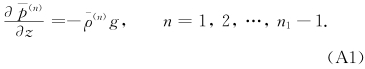
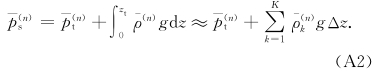
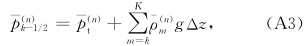
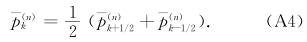
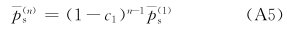
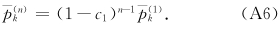
(1)Δ=0的情形。根据式(47),从式(A5)和(A6)可以得到
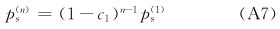
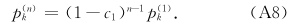
(2)Δ≠0的情形。这时从式(9)有
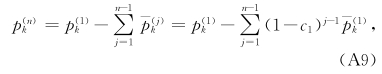
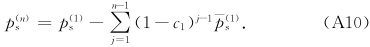
缩写词的全称如表 A1所示。
| 表 A1 缩写词的全称 Table A1 Full name of abbreviation |
| [1] | Arakawa A. 1966. Computational design for long-term numerical integrations of the equations of atmospheric motion [J]. J. Comput. Phys., 1 (1): 119-143. |
| [2] | Arakawa A, Lamb V R. 1997. Computational design of the basic dynamical processes of UCLA general circulation model [M].//Methods in Computational Physics. New York: Academic Press, 174-264. |
| [3] | Arakawa A, Suarez M J. 1983. Vertical differencing of the primitive equations in sigma coordinates [J]. Mon. Wea. Rev., 111 (1): 34-45. |
| [4] | Bubnová R, Hello G, Bénard P, et al. 1995. Integration of the fully elastic equations cast in the hydrostatic pressure terrain-following coordinate in the frame work of the ARPEGR/Aladin NWP system [J]. Mon. Wea. Rev., 123 (2): 515-535. |
| [5] | Cté, Jean, Gravel S, Méthot A, et al. 1998. The operational CMC-MRB Global Environmental Multiscale (GEM) model. Part I: design considerations and formulation [J]. Mon. Wea. Rev., 126 (6): 1373-1395. |
| [6] | Cullen M J P, Davies T, Mawson M H, et al. 1997. An overview of numerical methods for the next generation UK NWP and climate model [J]. The A. J. Robert Memorial Volume, Canadian Meteorological and Oceanographic Society, 35: 425-444. |
| [7] | Dudhia J. 1993. A nonhydrostatic version of the Penn State-NCAR mesoscale model: Validation tests and simulation of an Atlantic cyclone and cold front [J]. Mon. Wea. Rev., 121 (5): 1493-1513. |
| [8] | Dudhia J. 1995. Reply to Comments on "A nonhydrostatic version of the Penn State/NCAR mesoscale model: Validation tests and simulation of an Atlantic cyclone and cold front" by J. Steppeler [J]. Mon. Wea. Rev., 123 (8): 2573-2575. |
| [9] | 冯康, 等. 1978. 数值计算方法 [M]. 北京: 科学出版社, 22-23. Feng Kang, et al. 1978. Computational Methods [M]. (in Chinese). Beijing: Science Press, 22-23. |
| [10] | Gallus W A Jr, Rani M. 1996. A non-hydrostatic version of the NMCs regional Eta model [J]. Quart. J. Roy. Meteor. Soc., 122 (531): 495-513. |
| [11] | 季仲贞, 王斌, 曾庆存. 1995. 完全能量守恒差分法及其应用 [M]//数值天气预报的若干新技术. 北京: 气象出版社, 26-46.Ji Zhongzhen, Wang Bin, Zeng Qingcun, et al. 1995. Complete energy conservative finite difference method and its application [M].//Several New Techniques Concerning NWP (in Chinese). Beijing: China Meteorological Press, 26-46. |
| [12] | 廖洞贤, 孙岚. 2002. 关于尺度分析中的三个问题和尺度分析 [J]. 南京气象学院学报, 25 (4): 445-454.Liao Dongxian, Sun Lan. 2002. Scale analysis and its three problems [J]. Journal of Nanjing Institute of Meteorology (in Chinese), 25 (4): 445-454. |
| [13] | 廖洞贤, 孙岚. 2003. 中尺度非静力模式中常用气压分离技术的研究 [J]. 大气科学, 27 (2): 203-211.Liao Dongxian, Sun Lan. 2003. A study concerning the pressure separation technique used for current nonhydrostatic mesoscale models [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 27 (2): 203-211. |
| [14] | 廖洞贤. 2004. 完全弹性非静力模式 (动力部分) 的发展 //中国气象学会编. 推进气象科技创新加快气象事业发展 (上册). 北京: 气象出版社, 203-210.Liao Dongxian. 2004. Development of the complete compressible nonhydrostatic model (dynamic frame) [M].//Chinese Meteorological Society. Pushing the Scientific and Technical Innovation Forward and Speeding up the Development of Meteorological Cause (Vol. 1) (in Chinese). Beijing: China Meteorological Press, 203-210. |
| [15] | 廖洞贤. 2008. 数值天气预报中 "大量级差问题" 和解决问题的可能途径 [M]//模式设计、 数值试验、 数值模拟和有关的研究. 北京: 气象出版社, 111-119.Liao Dongxian. 2008. A problem of large magnitude difference occurring in numerical weather prediction equations and possible way for solving it [M].//Model Design, Numerical Experiment, Numerical Simulation and Related Studies (in Chinese). Beijing: China Meteorological Press, 111-119. |
| [16] | 刘式适, 刘适达. 1991. 大气动力学 (上册) [M]. 北京: 北京大学出版社, 169-185.Liu Shikuo, Liu Shida. 1991. Dynamic Meteorology (Vol. 1) (in Chinese) [M]. Beijing: Peking University Press, 169-185. |
| [17] | Satoh M. 2002. Conservative scheme for the compressible nonhydrostatic models with the horizontally explicit and vertically implicit time integration scheme [J]. Mon. Wea. Rev., 130 (5): 1227-1245. |
| [18] | Skamarock W C, Klemp J B, Dudhia J, et al. 2005. A description of the advanced research WRF version 2 . NCAR Tech. Note, NCAR/TN-468+STR, 31 . |
| [19] | Steppeler J, Hess R, Schttler U, et al. 2003. Review of numerical methods for nonhydrostatic weather prediction models [J]. Meteor. Atmos. Phys., 82: 287-301. |
| [20] | Steppeler J. 1995. Comments on "A nonhydrostatic version of the Penn State/NCAR mesoscale model: Validation tests and simulation of an Atlantic cyclone and cold front" [J]. Mon. Wea. Rev., 123 (8): 2572. |
| [21] | Stull R B. 1988. An Introduction to Boundary Layer Meteorology [M]. The Netherlands: Kluwer Academic Publishers Group, 669pp. |
| [22] | Tapp M C, White P M. 1976. A non-hydrostatic mesoscale model [J]. Quart. J. Roy. Meteor. Soc., 102 (432): 277-296. |
| [23] | Taylor K E. 1984. A vertical finite-difference scheme for hydrostatic and nonhydrostatic equations [J]. Mon. Wea. Rev., 112 (7): 1398-1402. |
| [24] | 薛纪善, 陈德辉, 等. 2008. 数值预报系统GRAPES的科学设计与应用 [M]. 北京: 科学出版社, 175-176.Xue Jishan, Chen Dehui, et al. 2008. The Scientific Design of GRAPES and Its Applications [M]. (in Chinese). Beijing: Science Press, 175-176. |
| [25] | Xue M, Droegemeier K K, Wong V. 2000. The advanced regional prediction system (ARPS)—A multi-scale nonhydrostatic atmospheric simulation and prediction model. Part I: Model dynamics and verification [J]. Meteor. Atmos. Phys., 75: 161-193. |
| [26] | 叶笃正, 李崇银, 王必魁. 1988. 动力气象学 [M]. 北京: 科学出版社, 82-92.Ye Duzheng, Li Chongyin, Wang Bikui. 1988. Dynamic Meteorology [M]. (in Chinese). Beijing: Science Press, 82-92. |
| [27] | Yeh K S, Cté J, Gravel S, et al. 2002. The CMC-MRB Global Environmental Multiscale (GEM) model. Part III: Nonhydrostatic formulation [J]. Mon. Wea. Rev., 130 (2): 339-356. |
| [28] | 曾庆存, 张学洪. 1987. 球面上斜压原始方程组保持总有效能量守恒的差分格式 [J]. 大气科学, 11 (2): 113-127.Zeng Qingcun, Zhang Xuehong. 1987. Available energy conserving schemes for spherical baroclinic primitive equations [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 11 (2): 113-127. |
| [29] | 张可苏, 周晓平. 1980. 非静力平衡模式中重力惯性波的传播、 结构和传播特征 //中央气象局气象科学研究所编. 第2次全国数值预报会议论文集 (1977年12月22-28日, 北京). 北京: 科学出版社, 196-206.Zhang Kesu, Zhou Xiaoping, 1980. The features of frequency spectrum, structure and propagation of gravitational-inertia waves in nonhydrostatic model //The Collected Papers of 2nd Conference of NWP (Dec. 22-28, 1977) (in Chinese). Beijing: Science Press, 196-206. |
| [30] | 朱禾, 孙岚, 廖洞贤. 2007. 大气数值模式空间分辨率的确定方法 [J]. 大气科学, 31 (3): 410-417.Zhu He, Sun Lan, Liao Dongxian. 2007. Determination of the spatial resolution required by the atmospheric numerical model [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 31 (3): 410-417. |
| [31] | 左瑞亭, 张铭 张东凌 等. 2004. 21层大气环流模式IAP AGCM-Ⅲ的设计及气候数值模拟 I. 动力框架 [J]. 大气科学, 28 (5): 659-674.Zuo Ruiting, Zhang Ming, Zhang Dongling, et al. 2004. Designing and climatic numerical modeling of 21-level AGCM (IAP AGCM-III) Part I. Dynamical framework [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 28 (5): 659-674. |
 2012, Vol.36
2012, Vol.36 


