2. 南京信息工程大学大气科学学院,南京 210044
3. 94701部队,安庆 246001
2. College of Atmospheric Science,Nanjing University of Information Science & Technology, Nanjing 210044
3. Unit 94701,PLA,Anqing 246001
当前,随着观测手段和种类的增加,资料同化技术在提高数值预报准确性方面发挥着越来越重要的作用。集合卡尔曼滤波(EnKF)(Evensen,1994)因其不需要切线性模式和伴随模式以及易于实现和移植(Evensen,2003)而受到广泛的关注和重视。尽管EnKF的优势是拥有流依赖(Flow-Dependent)的背景误差协方差,在理论上要优于当前的业务同化方案三维变分(3DVAR)方法(Gao et al.,1999),但当前EnKF仍存在着很多问题,使其在花费更多计算代价的情况下并没有在实际应用中取得相应的改进,而这其中最主要的原因就是滤波发散问题:错误估计背景误差协方差导致滤波器排斥或不能正确同化观测。许多因素能使EnKF产生滤波发散。十几年来,人们提出了许多方法来解决其中集合离散度过低(Anderson and Anderson,1999; Zhang et al.,2004; Anderson,2007a; Li et al.,2009),远距离虚假相关(Houtekamer and Mitchell,1998; Houtekamer and Mitchell,2001; Anderson,2007b; Hunt et al.,2007)以及模式误差(Dee and Da Silva,1998; Zheng et al.,2006; Danforth et al.,2007; Meng and Zhang,2007; Li et al.,2009)等问题,使得EnKF有了较大的改进。
但是,与四维变分(4DVAR)(Sun and Crook,1997; 许小永等,2004)方法相比,EnKF仍存在着收敛速度较慢的问题,这一问题不仅在天气尺度资料同化中出现(Yang et al.,2009),而且也在风暴尺度资料同化中出现(Caya et al.,2005)。对于发展速度快、生命史较短的中小尺度天气系统,缓慢的收敛速度很有可能使得EnKF错失最佳的预报时期。Kalnay and Yang(2010)指出,EnKF实现最优化分析的两个必要条件是:(1)集合均值与真值相近,(2)背景误差协方差能够代表真实误差的空间结构。在风暴尺度资料同化中,这两个条件往往得不到满足。首先,同化所用的缺乏风暴信息的初始估计与实际大气状态往往有较大的偏差。其次,由于风暴尺度中地转平衡关系不再适用,所使用的扰动也多为随机扰动(如Xue et al.,2006),不能很好地代表初始误差的空间分布。因此,在这一误差较大的初始估计和随机扰动的作用下,集合预报得到的背景误差协方差很难有效地代表预报误差的实际空间结构。而不准确的背景误差协方差就会导致滤波无法向正确的方向收敛,从而导致滤波发散。要解决这一问题,就要提高观测资料的利用效率,尽可能利用观测资料修正初始估计的误差。顺序资料同化的特点是无论观测在同化中是否被有效的利用,同一个观测资料只能使用一次。然而,Kalnay and Yang(2010)指出多次利用同一个观测资料进行同化在初始估计偏差较大的情况下是可以接受的。同时,Kalnay and Yang(2010)借鉴4DVAR的思想,提出了加快同化收敛速度的方案:原地踏步(running in place)方案,简称RIP。该方案在同化时涉及两个时间层,首先利用无代价(no cost)卡尔曼平滑(EnKS)(Yang et al.,2009)更新同化时刻之前某一时刻的背景场,然后用这一改进了的背景场再次向前预报到同化时刻并重复这一分 析——预报的循环,直到前后两次分析误差的差别减小到预先设定的阈值。这一方案进行迭代的目的就是为了在初始估计偏差较大的情况下尽可能多的从观测中提取信息,并进而达到改进同化分析结果,提高同化收敛速度的目的。Kalnay and Yang(2010)在准地转模式中的测试表明这一方法能够在很大程度上提高EnKF的收敛速度,并且在最终结果上优于3DVAR,而与4DVAR基本相当。
然而,针对这一包含迭代过程的同化方案的研究还处在起步阶段,还有很多问题没有得到讨论,例如存在模式误差时的同化和非常规观测的同化。要将RIP方案应用到实际观测的EnKF同化中,这两个问题是必须面对的。目前的模式只能对实际大气的运动规律做近似的估计,尤其是在各种参数化过程中,因此模式误差不可避免。同时,高时空分辨率的非常规观测的变量往往不是模式变量,RIP方案能否有效改进非常规观测同化的效果在Kalnay and Yang(2010)的研究中并没有得到讨论。此外,尽管Kalnay and Yang(2010)的研究动机是提高风暴尺度资料同化的收敛速度,但是RIP所用局地化的集合变换卡尔曼滤波(LETKF)算法(Hunt et al.,2007)目前在风暴尺度中并没有得到广泛的应用,而在风暴尺度资料同化中得到广泛应用的集合平方根滤波(EnSRF)算法(Whitaker and Hamill,2002)是否适用于这一方案则没有得到讨论。
针对这些尚未被研究的方面,本文借鉴RIP方案的设计思路并利用非同步算法(Sakov et al.,2010),在Lorenz96模式上设计了一个基于EnSRF算法(传统EnSRF)的包含迭代过程的同化方案——迭代集合平方根滤波(iterative EnSRF,简称iEnSRF)来检验EnSRF算法在RIP方案中应用的可行性,并讨论其在非完美模式下的同化效果和对非常规观测同化的效果。与RIP方案不同,iEnSRF方案通过Sakov et al.(2010)提出的非同步算法来实现向后分析,更新分析时刻前的背景场。这一iEnSRF方案的设计将在本文的第二部分中给出。同化试验的设计和结果在第三部分中给出。试验讨论了无模式误差和有模式误差情况下的同化以及针对不同类型观测的同化,对比了传统EnSRF和iEnSRF的同化效果以及他们对背景误差协方差的影响,并对他们分析结果的合理性进行了讨论。同时,试验还讨论了iEnSRF的一个褪化情况,即iEnSRF涉及的两个时次间隔为零时的情况。最后 第四部分是全文的总结。
2 传统EnSRF和迭代EnSRF 2.1 传统EnSRF方案由Whitaker and Hamill(2002)提出的EnSRF方案是EnKF中的一个重要的分支,该方案对传统的EnKF更新方程进行了调整,使其可以在不低估分析误差协方差的情况下不对观测进行扰动,避免了由扰动观测带来的采样误差及其产生的滤波发散问题。EnSRF的计算分为两步:

其中,(1)式为集合预报部分,X表示模式预报的状态向量,M代表预报模式,a代表分析估计,b代表预报估计,i表示第i个成员。(2)式和(3)式为EnSRF同化tn时刻第j个观测yj°的方程,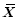 代表集合平均,Xj'代表集合扰动;K=PbHT(HPbHT+ R)-1代表卡尔曼增益矩阵,其中H代表线性观测算子,
代表集合平均,Xj'代表集合扰动;K=PbHT(HPbHT+ R)-1代表卡尔曼增益矩阵,其中H代表线性观测算子,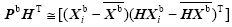 代表tn时刻通过统计集合成员得到的模式变量和观测变量之间的背景误差协方差,
代表tn时刻通过统计集合成员得到的模式变量和观测变量之间的背景误差协方差,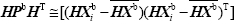 代表tn时刻通过统计集合成员得到的观测变量的背景误差协方差,R代表观测误差协方差,α是EnSRF为解决由不扰动观测导致的分析误差协方差被低估而引入的小参数,其在单一观测条件下的解为:
代表tn时刻通过统计集合成员得到的观测变量的背景误差协方差,R代表观测误差协方差,α是EnSRF为解决由不扰动观测导致的分析误差协方差被低估而引入的小参数,其在单一观测条件下的解为: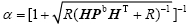 (Maybeck,1979)。在引入α后,EnSRF的分析误差协方差Pa变为(I-αKH)Pb(I-αKH)T,与Kalman滤波理论中的分析误差协方差(I-αKH)Pb(I-αKH)T+KRKT相等,解决了因为不扰动观测而导致低估分析误差协方差的问题。
(Maybeck,1979)。在引入α后,EnSRF的分析误差协方差Pa变为(I-αKH)Pb(I-αKH)T,与Kalman滤波理论中的分析误差协方差(I-αKH)Pb(I-αKH)T+KRKT相等,解决了因为不扰动观测而导致低估分析误差协方差的问题。
2.2 迭代EnSRF方案
在传统的EnSRF方案中,同一个观测只能使用一次。这一特征使得某个观测即使没有被正确同化也将被弃置不用,大大降低了观测资料的使用效率,同时也会限制同化改进的效果,甚至出现相反的效果。因此,根据Kalnay and Yang(2010)的设计思路以及Sakov et al.(2010)对非同步算法的讨论,本文设计了一个包含迭代过程的同化方案(iEnSRF)。Sakov et al.(2010)指出非分析时刻得到的观测可以通过观测时刻与分析时刻间的背景误差协方差来更新分析时刻的背景场。根据这一结论,本文设计的iEnSRF在分析过程中将包含两个时次的背景场,并将在t-dt时刻和t时刻之间进行分析和预报的迭代,以达到充分提取观测信息,提高每一时次同化效果的目的。其工作流程图如图 1所示:
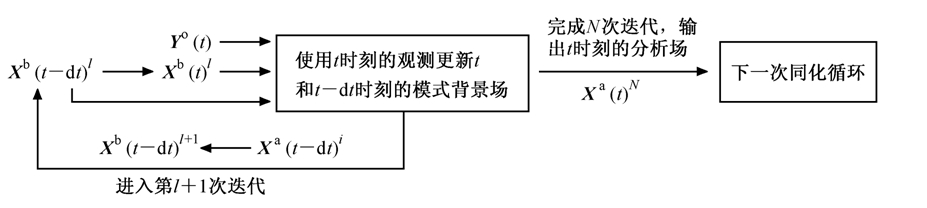 |
图 1 iEnSRF工作流程图(l表示第l次迭代) Fig.1 The working flow chart of iEnSRF scheme. Superscript l represents the l th iteration |
在分析同化部分,用于分析的背景场Xb包含了两个时次(Xb(t),Xb(t-dt))T,因此可以将Xb(t-dt)看成是一组新增的模式变量。这样,在新的分析方程中,对于第j个观测yj°,Xb(t)的分析方程可以完全保持原EnSRF方程(2)、(3)的形式,而相应的Xb(t-dt)的更新部分表达式为:

其中,
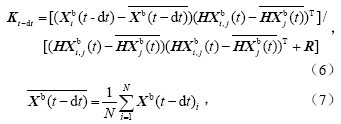
通过方程(4)可以得到t-.dt时刻的分析平均,而通过方程(5)则可得到t-.dt时刻的分析扰动。由Kt-dt表达式可见,更新t-.dt时刻所用的卡尔曼增益矩阵与t时刻的增益矩阵只是在分子上有所不同,前者的分子是前后两个时刻间的背景误差协方差,而后者的分子是同一时刻的背景误差协方差。这一实现方案与Sakov et al.(2010)的讨论中略有不同,不同之处在于背景场向量中引入了两个时次的背景场。这一设计的主要原因是EnSRF是一个顺序算法,只能一个接一个地更新观测。这样在其分析过程中就会隐式地更新了观测空间的背景场。因此,在iEnSRF的背景场向量中包含t时刻的背景场将使得这一隐式的更新得以保留,从而保证iEnSRF分析的合理性。
在迭代过程中,iEnSRF在分析得到Xa(t-dt)后将其作为t-.dt时刻新的背景场并再次积分到t时刻得到新的Xb(t),然后利用方程(4)、(5)对新的Xb(t-dt)进行分析,之后不断重复这一分析——预报的过程直到达到优化Xa(t)的目的。
3 试验设计和结果 3.1 试验设计试验所用模式为一维非线性Lorenz96模式,根据Lorenz and Emanuel(1998)的工作,模式的控制方程为:
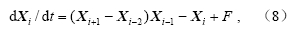
其中,X为模式变量,i为模式空间的格点编号,F表示定常强迫,模式采用周期边界。这一模式虽然非常简单,但是包括了大气运动的几个主要基本特征:平流、耗散和外强迫,因此在资料同化方法的研究中得到了大量的应用(Whitaker and Hamill,2002; Hunt et al.,2004)。首先以给定参数和初值单独运行Lorenz96模式(控制试验),其结果作为评估同化效果的真值。控制试验的设置为:模式空间格点总数为40,只有一个模式变量X,积分时间步长dt 为0.05单位时间,外强迫 F 为8.0,总的积分步数为7000步。同化从1001步开始,之前作为spin-up时间。
为讨论iEnSRF在完美模式和有误差模式下的表现,试验共分为三组:完美模式试验,有误差模式试验和参数扰动试验。所有试验的集合成员数均为40,其中在完美模式试验中,强迫项F 的取值为8.0,与真值相同;有误差模式中F的取值为9.6,比真值高20%;而在参数扰动试验中,这一有误差的F(F=9.6)将被加入一组均值为0,方差为0.8的扰动,以代表模式的不确定性。为讨论iEnSRF同化不同类型观测的表现以及对背景误差协方差的影响,在上述每组试验下在进行三种不同类型观测的试验,观测的变量分别为:模式变量 X(OT1)、模式变量的梯度ΔX(OT2)和模式变量的拉普拉斯Δ2(OT3)。设计非模式变量观测是考虑到当前新型观测的变量多为非模式变量,因此需要考察iEnSRF对非模式变量的同化能力,而设计两个不同类型的非模式变量观测是要检测iEnSRF对不同非模式变量的同化效果是否相近。所有观测都取在控制试验中X的极值点上,以代表观测能够得到模式状态的主要特征,但对细节部分不能进行很好的观测。每次同化所使用的观测数量最少为14个,最多为30个,平均为22个。所有观测的误差均方差均设为0.1。为比较iEnSRF和传统方案的差异,除了在iEnSRF进行上述试验的测试外,还将这些试验应用于传统EnSRF方案和一个类似于3DVAR中外循环(Outer loop)的方案(EnSRFMA),这一方案也可以视为当迭代时间间隔dt 为0时的iEnSRF的褪化方案。所有同化试验都应用了五阶距离相关函数(Gaspari and Cohn,1999)进行局地化和乘数法进行协方差膨胀。除了iEnSRF方案中分析t-dt时刻背景场时使用的局地化距离为3个格距,其他试验中的局地化距离均为2个格距。考虑到迭代方案中反复同化有可能过度降低集合离散度,对乘数法进行了简单自适应调整:以观测空间的均方根误差与观测空间的离散度的比值
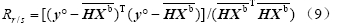
为参考,如果Rr/s小于1.05,协方差膨胀系数为1.01,如果Rr/s大于1.05,协方差系数为Rr/s,上限为1.5,即膨胀的上限是50%。与往常Lorenz96模式的试验不同,在本文中,所有试验的分析间隔设为10倍 dt。没有选择每积分一步就同化的原因是在实际同化中获取观测的时间间隔往往相对较长,常规探空资料12小时得到一次观测,卫星资料最快1小时得到一次观测,即使高频的多普勒天气雷达资料仍需要6分钟才能得到一次观测,因此不可能每积分一步就同化一次。此外在试验中还发现扰动的非线性项在积分10步之后增长速度发生突变,开始快速增长,当离散度为100量级时,积分10步后非线性项的量级与线性项相当,所以为保证分析结果的合理性,将分析间隔选为10倍dt(线性项和非线性项的计算方式将在随后的部分中给出)。在完美模式试验的每次同化中,使用 iEnSRF 方案的试验和使用EnSRFMA方案的试验的迭代的次数为5次。而在有误差模式的试验中,相应的迭代次数为4次。iEnSRF方案所涉及到的两个时间层之间的间隔为1倍 dt。
3.2 结果分析 3.2.1 误差演变的分析
考虑到设计iEnSRF的目的是提高每次单一时次同化的改进效果,实现更快的收敛速度和最终更小的误差,首先分析前20次同化中各试验的均方根误差(Root Mean Square Error 或RMSE)误差演变(如图 2所示)。很明显,在完美模式中iEnSRF的效果最好。无论是在OT1、OT2还是OT3的同化中,iEnSRF的前3次的同化都能够产生大于传统EnSRF的改进,并且同化后再次预报到分析时刻的误差相对较小。当同化进行到第4、第5次时,iEnSRF的分析误差和预报误差已经远小于传统EnSRF误差水平,并且在之后快速收敛。OT1的试验中iEnSRF在15次同化之后开始稳定,OT2的试验中iEnSRF的分析在第10次同化之后开始稳定,而OT3的试验中该方案也在15次同化后开始稳定,并且都是稳定在一个较小的误差水平。传统EnSRF和EnSRFMA在OT1观测的同化中能够逐步减小误差,但再次预报的误差增长较快从而导致收敛速度较慢。在OT2的同化中传统EnSRF在前20步同化中没有收敛,误差在较高水平上振荡,而EnSRFMA则表现出与iEnSRF类似的效果,但其同化后再次预报的误差增长比iEnSRF大。在OT3的同化中传统EnSRF同样没有能够在前20次同化中收敛,与OT2的同化类似,而EnSRFMA则能逐步减小分析的误差,但再次预报的误差偏大,表现出其在同化OT1时相似的形式。由以上数据可见,在完美模式下,iEnSRF达到了设计的预期目的,能够提高单次同化的改进效果,加快收敛的速度。同时也需要看到,观测的类型对iEnSRF的同化效果是有影响的,不同类型观测所反映真实模式状态的信息量不同以及与模式状态变量的相关性不同可能是导致同化方案对观测类型响应不一的原因。EnSRFMA对不同观测的同化效果差异较大并且预报误差相对iEnSRF较大,这一现象说明如果仅仅简单地对一个背景场简单重复同化多次并不能稳定的改进分析的效果,因为从理论上看EnSRF同化一次后的分析场已经是线性最优,对分析场再次用同样的观测进行同化不符合理论要求,除非使用不一样的背景误差协方差,而这一点正是iEnSRF能够做到的。
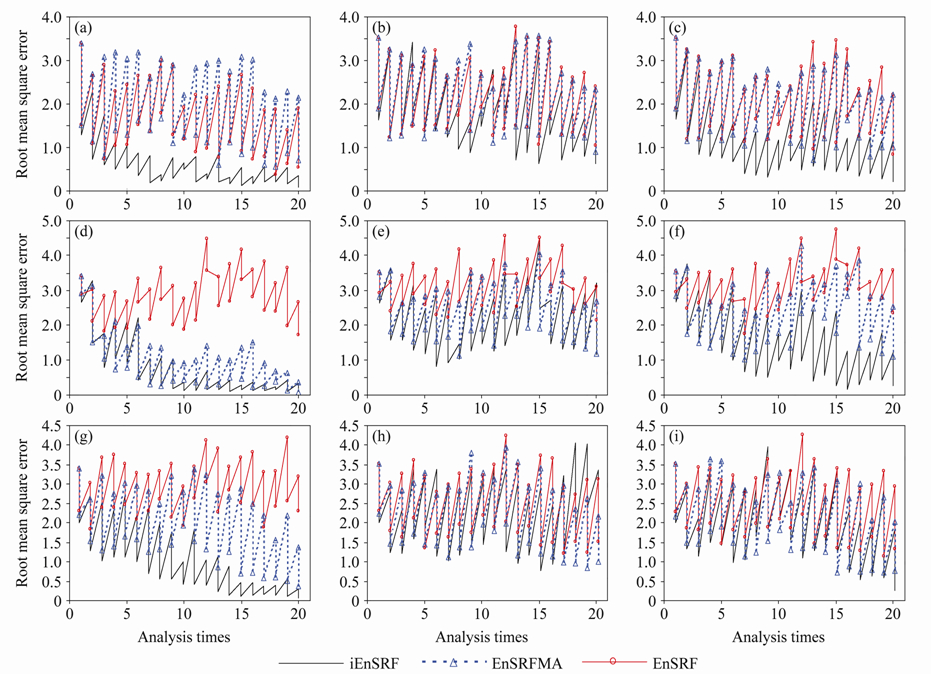 |
图 2 (a-c)OT1、(d-f)OT2和(g-i)OT3试验均方根误差在前20次同化中随时间的演变:(a、d、g)完美模式试验;(b、e、h)有误差模式试验;(c、f、i)参数扰动试验 Fig.2 The evolution of RMSE in the first 20 analysis cycles for experiments using(a-c)OT1,(d-f)OT2,and (g-i)OT3:(a,d,g)Perfect model is used;(b,e,h)imperfect model is used;(c,f,i)imperfect model with parameter perturbation is used |
尽管iEnSRF在完美模式下的表现相当好,但是当模式存在不可忽略的误差时,正如预期的一样,依靠预报模式来驱动背景误差协方差的迭代方案明显受到了模式误差的影响,分析效果不稳定,部分时刻能够产生相对传统方案较大的改进,而部分时刻的改进则较传统方案偏小,并且再次预报的误差也偏大。iEnSRF在另两个观测的试验中也表现出了相同的现象,这与EnKF方法本身对模式误差比较敏感有关,也说明更加依赖模式准确度的iEnSRF将对模式误差更为敏感。因此当模式误差存在时,应用iEnSRF将难以达到产生较大改进的效果,甚至可能会有负效果。
对有误差的模式参数进行扰动之后,集合预报系统对真实模式状态的估计能力提升,也使得iEnSRF的分析效果得到改进。在OT1和OT2两种观测的同化中,尽管受到模式误差的影响,iEnSRF同化后再次预报的误差相对较大,但其同化后能够将分析误差量级控制在10-1,并且在同化接近20次的时候其预报误差也能基本控制在1.5以下;而在OT3的同化中,iEnSRF的改进效果尽管与传统EnSRF方案和EnSRFMA相比不是很明显,但相对与不估计模式误差的情况仍有很大改进,第20次同化时分析误差已经减小到1.0以下。相对于iEnSRF方案在估计模式误差后产生的较大改进,传统EnSRF的改进效果则不明显,误差在分析和预报之间大幅振荡,而EnSRFMA的表现与传统EnSRF基本相似,在OT2观测的同化中略好于传统方案。扰动模式物理参数的试验表明iEnSRF能够较好地利用改进的集合预报系统来提高分析效果,而传统EnSRF则不能很好地利用改进的集合预报系统提高分析效果。
3.2.2 背景误差协方差的分析为考察分析结果的合理性,本文对每次同化前的离散度与均方差的空间相关进行了分析,其中相关系数:
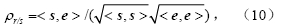
s包括各个格点上的离散度si(i=1,2,…,40),e包括各个格点上的均方差ei(i=1,2,…,40)。前20次同化中rr/s随时间的演变如图 3所示。
 |
图 3 (a-c)OT1、(d-f)OT2和(g-i)OT3试验中预报的离散度和实际误差均方差的空间相关系数在前20次同化中随时间的演变:(a、d、g)完美模式试验;(b、e、h)有误差模式试验;(c、f、i)参数扰动试验。黑色直线对应样本数为40时通过99%信度检验的相关系数 Fig.3 The spatial correlation coefficient between ensemble spread and real error variance in the first 20 analysis cycles for experiments using(a-c)OT1,(d-f)OT2,and (g-i)OT3:(a,d,g)Perfect model is used;(b,e,h)imperfect model is used;(c,f,i)imperfect model with parameter perturbation is used. The dark straight line shows the correlation coefficient passing 99% confidence level test with 40 samples |
从图 3a、d、g中可以看到,在完美模式下,iEnSRF对背景误差协方差的改进比较明显。同化前预报估计的误差与实际误差的相关系数很低,没有通过99%的信度检验,经过iEnSRF同化后,预报误差与实际误差的相关大多能通过信度检验,而传统EnSRF和EnSRFMA估计的误差空间分布则没能较好且稳定的代表真实误差的空间结构。其中在OT1的同化中,iEnSRF试验的前6次同化的离散度和真实误差相关系数迅速上升,对应了图 2中均方根误差迅速下降的阶段,尽管随后误差减小到一定程度时相关系数有所下降,但仍能通过信度检验;而传统EnSRF和EnSRFMA在前6次同化中估计的误差则与真实误差相关程度较低,之后相关系数变化与iEnSRF相似,但此时iEnSRF已经基本将误差减小并稳定在一个比较小的数值上,而另两种方案的误差仍然比较大且不稳定。在OT2和OT3的同化中,iEnSRF的优势更加明显,其预报的误差估计与真实误差的相关基本都能稳定通过99%的信度检验,并且部分时刻的相关系数接近或超过0.8,基本能够代表真实误差的空间结构,对应了图 2中误差迅速收敛的情况。而传统EnSRF估计的误差空间结构与真实结构的相关系数则基本在信度检验的阈值之下。因此传统EnSRF尽管同化能够产生一定的改进,但较差的背景误差估计使得改进效果不足以抵消随后预报产生的误差增长,使得滤波难以收敛。尽管EnSRFMA估计的背景误差协方差与传统EnSRF处于同一水平,但其产生的误差的减小幅度在OT2中与iEnSRF相似并在OT3的同化中优于传统EnSRF,这种不一致的现象仅通过空间相关系数和均方差随时间的变化难以得出合理的解释,需要做进一步的分析。
在有误差模式下,所有试验得到的相关系数都不理想。在OT1的同化中,尽管iEnSRF得到的相关系数在大部分时候比另两个试验要高,但是基本只是在信度检验的阈值附近振荡,而且很不稳定,对应了图 1中该方案时好时坏的表现;而在OT2和OT3的试验中,所有方案产生的相关系数基本都在信度检验阈值之下而且水平基本相当,所以同化的效果也十分类似。在有不可忽略误差的模式下,如果没有对模式误差进行处理,不准确的模式将驱动出不准确的误差协方差,而iEnSRF需要多次应用模式来驱动产生新的背景误差协方差估计,错误的模式将使得这一估计越来越差。因此,在有误差模式下直接应用iEnSRF方案将不能产生预期的效果,并且还将花费巨大的计算代价。
对有误差的模式参数进行扰动之后,可以看到iEnSRF在OT1和OT2的同化中产生的相关系数已经得到了明显的改善。其中iEnSRF同化OT1的表现已经和完美模式相似,相关系数基本都在信度检验阈值之上,并且没有出现未扰动参数之前产生负相关的情况;而在OT2的同化中,尽管同化初期的相关系数改进速度较慢,但第7次同化之后其相关系数也能超过信度检验的阈值,对应了图 2中iEnSRF分析误差远小于传统EnSRF分析误差的情况,说明在更加准确的集合平均和扰动作用下滤波器可以得到最优的分析结果;在同化OT3的试验中,iEnSRF产生的相关系数改进不明显,使得同化产生的误差减小程度与其他方案相差不大,这一现象表明iEnSRF并不是对所有类型的观测都能产生很好的改进效果。传统EnSRF和EnSRFMA在同化OT3的试验中产生的相关系数则相对前一组忽略模式误差的试验没有明显的改变,尽管他们在OT1的试验中其对误差的整体估计水平有所提升,但其相关系数仍在信度检验阈值附近振荡,很多时刻估计的背景误差协方差仍不可信,因此对误差的改进效果也不明显;而他们在OT2和OT3的试验中这两个试验得到的相关系数大部分在信度检验阈值之下,对应了与前一组试验相似的误差分析结果。
3.2.3 同化结果合理性的分析为了检验分析结果的合理性,本文对集合中线性项和非线性项的量级进行了比较。这主要是考虑到EnKF的背景误差协方差传播方程被假设为线性方程:Pt+1b=MPtaMT,其中M为线性预报方程。当EnKF被应用于非线性预报模式时,如果非线性项的量级小于线性项的量级,则可以近似认为EnKF的线性假设得到满足。根据Lorenz96模式的控制方程,与扰动有关的线性项为
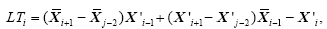 ,其中,
,其中,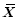 为集合平均值,X'为扰动值,i和j分别 表示第i个格点和第j个格点;非线性项为
为集合平均值,X'为扰动值,i和j分别 表示第i个格点和第j个格点;非线性项为 。考虑到-X'对扰动起到的是耗散作用,因此在后面的计算中将略去这一项。为计算简便,计算是只使用同化前的集合来近似估计预报过程中这两项的变化的量级。前20次同化中非线性项与线性项量级的比值
。考虑到-X'对扰动起到的是耗散作用,因此在后面的计算中将略去这一项。为计算简便,计算是只使用同化前的集合来近似估计预报过程中这两项的变化的量级。前20次同化中非线性项与线性项量级的比值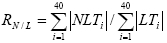 随同化次数的演变如图 4所示。
随同化次数的演变如图 4所示。
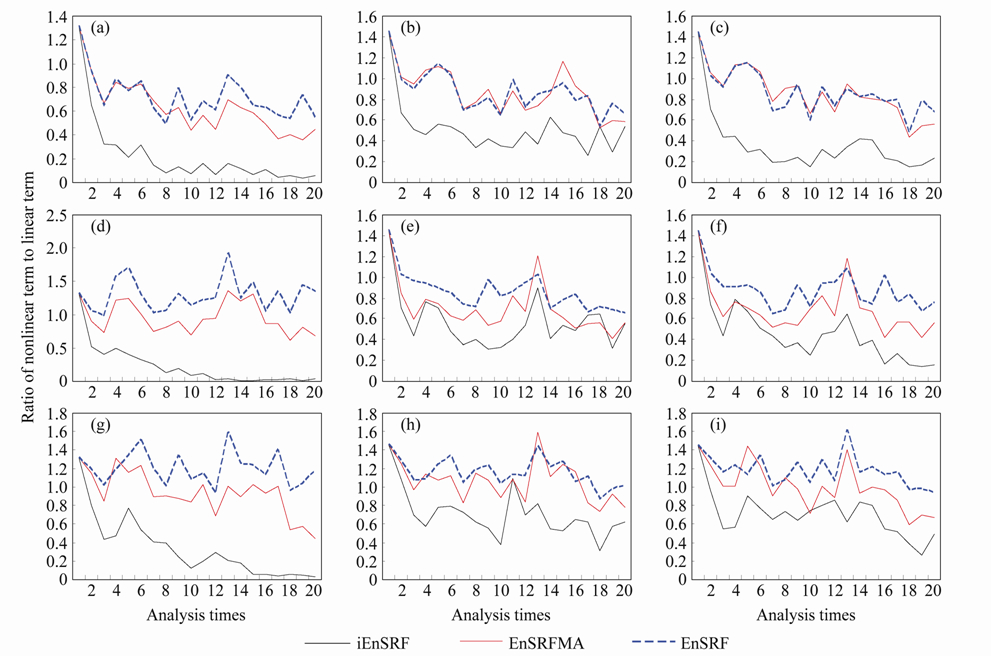 |
图 4 (a-c)OT1、(d-f)OT2和(g-i)OT3试验中扰动预报方程的非线性项和线性项量级的比值在前20次同化中随时间的演变:(a、d、g)完美模式试验;(b、e、h)有误差模式试验;(c、f、i)参数扰动试验 Fig.4 The evolution of quantity ratio of nonlinear term to linear term in perturbation forecast equation in the first 20 analysis cycles for experiments using(a-c)OT1,(d-f)OT2,and (g-i)OT3:(a,d,g)Perfect model is used;(b,e,h)imperfect model is used;(c,f,i)imperfect model with parameter perturbation is used |
图 4的结果与图 3、图 2基本对应。在完美模式下,iEnSRF的三个试验中的非线性项与线性项的比值迅速下降,最后都基本达到或小于0.1的水平,对应线性项的量级比非线性项大一个量级左右,因此iEnSRF的分析结果基本是在近似满足EnKF线性假设的条件下得到的,滤波器在近似符合理论条件下得到的分析结果也相对接近理论目标——线性最优。而传统EnSRF和EnSRFMA得到的比值则相对较大,在OT3的试验中非线性项的量级甚至大于线性项的量级。造成这一现象的原因是这两个方案单次同化产生的改进比较小,使得相应的集合离散度仍然较大,较大的扰动在非线性的作用下使得非线性项能够迅速增长。因此两个方案在线性假设得不到满足的条件下分析效果也相对不理想。从总体上看,尽管EnSRFMA中两项的比值相对iEnSRF较大,但相对传统EnSRF方案还是略有改进。在更好满足理论上的线性假设情况下,EnSRFMA在同化OT2和OT3时得到相对传统EnSRF更好的效果具有一定的合理性,这一现象部分解释了前面EnSRFMA在背景误差协方差与传统EnSRF水平相当时反而得到更好效果的原因。当模式存在误差时,iEnSRF各个试验中两项的比值均比完美模式下的比值大,基本都在0.4之上,对应了线性部分的量级仅比非线性项略大,非线性的影响不能忽略,使得分析结果在理论假设不能够满足的条件下难以有大的改进。而另两个试验的情况与完美模式基本差别不大,对应了图 1中的分析误差随时间的变化与完美模式下类似,均难以收敛。在参数扰动试验中,iEnSRF在OT1和OT2的试验中得到的RN/L值相对前一组试验得到了较大的改进。尽管没有达到完美模式下的水平,但iEnSRF试验中的RN/L量级相对另两个方案的试验已经明显减小。因此,在这两类观测的试验中,iEnSRF方案得到了更为理想的分析结果,而传统EnSRF和EnSRFMA的表现则与前两组试验基本一致:非线性项的量级仍然较大,使得理论上的线性假设仍得不到满足,对应了图 1中两者分析结果与有误差模式下的结果类似。OT3试验中3个同化方案的表现也与前一组试验基本相似,iEnSRF对分析的改进不大。
3.2.4 平均同化效果的分析最后,对600次同化的平均状况进行分析,以检验iEnSRF方案的平均效果。本文以600次同化中预报误差和分析误差的平均值以及相应的平均离散度偏离平均均方差平均值的比率作为评估标准,如图 5、图 6所示。
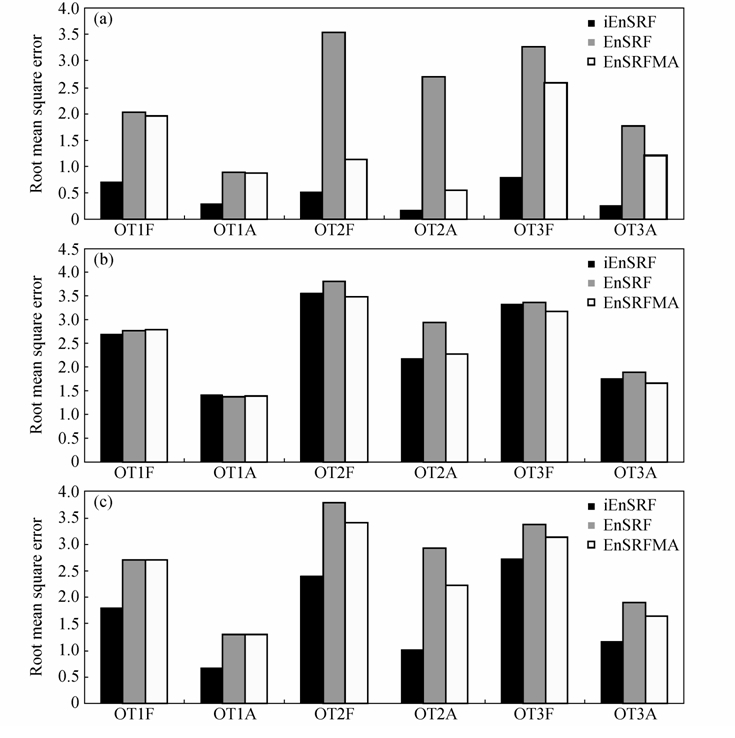 |
图 5 600次同化循环的平均预报均方差和分析均方差:(a)完美模式试验;(b)有误差模式试验;(c)参数扰动试验,其中OT1,OT2和OT3分别代表试验所用的观测类型;A和F分别代表分析和预报 Fig.5 The average forecast RMSE and analysis RMSE in 600 assimilation cycles for experiments using(a)perfect model,(b)imperfect model,and (c)imperfect model with parameter perturbation,where OT1,OT2 and OT3 represent the observation types used in experiments respectively; A and F indicate the analysis and forecast respectively |
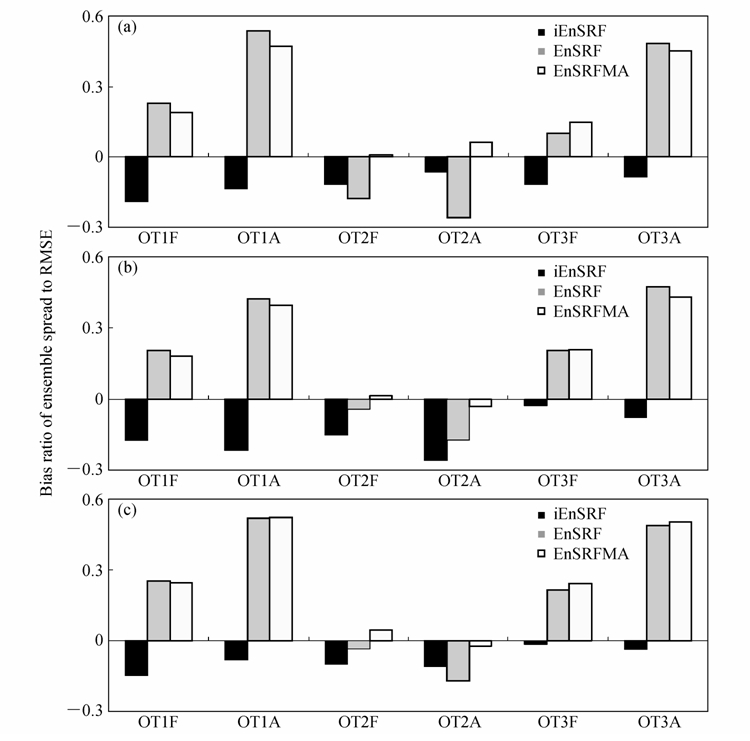 |
图 6 600次同化中平均离散度偏离平均均方差的比率,其余同图 5 Fig.6 As in Fig. 5,but for the bias ratio of average ensemble spread to average RMSE in 600 assimilation cycles |
从平均均方根误差上看,iEnSRF在完美模式中的表现非常好,基本保持了其在前20次同化中产生的优势。在三种观测的试验中,600次iEnSRF同化的平均分析误差在0.5以下,而同化后再次预报的误差也能够抑制在1.0以下,相对传统EnSRF提升超过50%,表明完美模式下iEnSRF方案的对同化效果的改进是明显且稳定的。而传统EnSRF尽管能够将平均分析误差控制在1.0以下,但再次预报的误差迅速上升超过2.0,意味着传统方案分析结果能够预报的时间不长。EnSRFMA同化结果的平均特点也和前20次同化的特点相似,在OT1的同化中与传统EnSRF方案基本相当,在OT2的同化中效果远好于传统方案,对OT3的同化结果也好于传统方案,但其对三种观测试验的分析误差都高于iEnSRF方案。同时可以看到,对于观测变量直接是模式变量的观测,传统EnSRF的分析效果还是能够接受的,但是对于非模式变量的观测(OT2和OT3),传统方案则不能得到理想的结果,结合前20次同化和600次同化的平均结果来看,传统方案始终没有能够收敛,即使收敛也是在一个误差比较大的水平,达不到大幅改进初始场的效果。从图 6中可以看到,完美模式下,除了OT2的试验,传统EnSRF和EnSRFMA在另两种观测的试验中产生的平均离散度大于均方差,其中分析场的离散度超出均方差30%以上,明显高估实际误差的量级并造成其非线性项量级偏大,使得滤波器的线性假设得不到满足。尽管iEnSRF得到的分析场和预报场的离散度相对均方差小,但根据离散度与均方差比值的期望值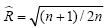 (Murphy,1988),其中n为集合成员数,40个样本对应的期望比例是0.716,对应离散度低于均方差接近30%,因此,iEnSRF所对应的离散度量级仍然是合理的,并且略小的离散度有利于减小非线性作用造成的影响。当模式存在误差时,所有同化方案的平均效果都低于完美模式下的效果(图 5b)。其中iEnSRF效果下降的幅度最大,分析误差和预报误差平均增长200%以上,表明iEnSRF方案在充分利用模式的同时也增加了对模式误差的敏感程度。而传统EnSRF方案的分析误差下降幅度最小,除了OT1试验中分析误差和预报误差相对完美模式上升不到50%外,OT2和OT3的试验与完美模式相差不大。EnSRFMA受模式误差的影响与iEnSRF方案相似,误差增长幅度较大。综合前20次同化的结果和600次同化的平均结果可以看出直接在有误差的模式上使用iEnSRF方案将不能得到预期的效果,并且耗费巨大计算代价,尽管在非模式变量的观测中该方案仍然能够取得相对传统方案的改进。从离散度的角度看,三种同化方案在有误差模式下的离散度量级都高于期望值,并且传统方案和EnSRFMA的离散度量级大于均方差量级,因此同化效果较差的主要原因不在离散度的量级上,而是在离散度的空间结构上。尽管背景误差的量级没有被低估,但是使用低于信度检验的背景误差相关关系将不能得到理想的分析结果。当有误差的模式参数经过扰动后,iEnSRF又能够产生明显的改进(图 5c)。在OT1和OT2的同化中,iEnSRF方案再次得到了相对传统EnSRF方案50%以上的改进,而另两个方案的结果则依然和扰动参数之前的效果相当,表明无论是在同化的初期状还是数百次同化的平均,iEnSRF方案都能够利用改进了的集合预报系统来提高其分析的效果,而传统方案和EnSRFMA方案则对同化系统的改进并不敏感,改进的集合预报系统并没有为其分析结果带来相应的改进。各个试验方案在扰动模式参数的情况下的离散度量级与完美模式和有误差模式的情况基本相同,表明当离散度的量级大幅低于均方差的量级时,同化效果的改进程度主要与离散度的空间结构的准确性有关,当离散度的空间结构能够比较准确地估计真实误差的空间结构时,即使其量级偏小,但仍能取得很好的分析效果,而当其所反映的空间结构偏离真实误差结构较多时,即使离散度的量级较大,也不一定能得到理想的结果。
4 总结与讨论
(Murphy,1988),其中n为集合成员数,40个样本对应的期望比例是0.716,对应离散度低于均方差接近30%,因此,iEnSRF所对应的离散度量级仍然是合理的,并且略小的离散度有利于减小非线性作用造成的影响。当模式存在误差时,所有同化方案的平均效果都低于完美模式下的效果(图 5b)。其中iEnSRF效果下降的幅度最大,分析误差和预报误差平均增长200%以上,表明iEnSRF方案在充分利用模式的同时也增加了对模式误差的敏感程度。而传统EnSRF方案的分析误差下降幅度最小,除了OT1试验中分析误差和预报误差相对完美模式上升不到50%外,OT2和OT3的试验与完美模式相差不大。EnSRFMA受模式误差的影响与iEnSRF方案相似,误差增长幅度较大。综合前20次同化的结果和600次同化的平均结果可以看出直接在有误差的模式上使用iEnSRF方案将不能得到预期的效果,并且耗费巨大计算代价,尽管在非模式变量的观测中该方案仍然能够取得相对传统方案的改进。从离散度的角度看,三种同化方案在有误差模式下的离散度量级都高于期望值,并且传统方案和EnSRFMA的离散度量级大于均方差量级,因此同化效果较差的主要原因不在离散度的量级上,而是在离散度的空间结构上。尽管背景误差的量级没有被低估,但是使用低于信度检验的背景误差相关关系将不能得到理想的分析结果。当有误差的模式参数经过扰动后,iEnSRF又能够产生明显的改进(图 5c)。在OT1和OT2的同化中,iEnSRF方案再次得到了相对传统EnSRF方案50%以上的改进,而另两个方案的结果则依然和扰动参数之前的效果相当,表明无论是在同化的初期状还是数百次同化的平均,iEnSRF方案都能够利用改进了的集合预报系统来提高其分析的效果,而传统方案和EnSRFMA方案则对同化系统的改进并不敏感,改进的集合预报系统并没有为其分析结果带来相应的改进。各个试验方案在扰动模式参数的情况下的离散度量级与完美模式和有误差模式的情况基本相同,表明当离散度的量级大幅低于均方差的量级时,同化效果的改进程度主要与离散度的空间结构的准确性有关,当离散度的空间结构能够比较准确地估计真实误差的空间结构时,即使其量级偏小,但仍能取得很好的分析效果,而当其所反映的空间结构偏离真实误差结构较多时,即使离散度的量级较大,也不一定能得到理想的结果。
4 总结与讨论
针对EnKF收敛较慢的问题,本文借鉴Kalnay and Yang(2010)的RIP方案,构建了一个基于EnSRF算法的iEnSRF方案,并利用三种不同类型观测详细讨论了这种iEnSRF方案在无模式误差和有模式误差情况下的同化效果。试验结果表明:
(1)在完美模式下,iEnSRF同化常规观测的效果远远优于传统EnSRF,并能够更加有效地同化非常规观测。而EnSRFMA则能够相对改进对非常规观测的同化。
(2)在有误差的模式下,如果忽略模式误差,iEnSRF对所有观测的同化效果与传统EnSRF相当,甚至在同化非常规观测时出现负效果。
(3)如果能够有效对模式误差进行估计或处理,iEnSRF能够更好地利用改进后的集合预报系统来提高其分析结果,而传统方案和EnSRFMA则不能很好地利用改进的集合预报系统提高其结果。
(4)背景误差协方差的空间结构的准确性而不是其量级是影响同化分析效果的主要原因。即使离散度的量级略小于均方差的量级,只要其空间结构与真实误差的空间结构相似就能得到比较好的分析效果,而即便离散度的量级大于均方差的量级,不可信的误差空间结构估计仍会造成同化效果不佳。
(5)EnKF方法中背景误差协方差传播的线性假设得到近似满足的程度越高,同化分析结果的合理性就越高,相应的效果也会更好。尽管EnSRFMA估计的误差的空间结构的准确性与传统EnSRF水平相当,但由于其滤波过程中对线性假设更好的满足使得其在OT2和OT3的试验中取得了相对更好的效果,而iEnSRF则由于对线性假设满足的程度最高而使其分析结果最好。
尽管iEnSRF在本文的试验中表现良好,但是这种方案仍处在初步设计阶段,还有很多不完善之处。相对于传统方案,iEnSRF增加了几个需要调整的参数:分析时间间隔、迭代次数和分析前后两个时次时使用的膨胀系数、局地化距离等,这些参数在本文中的设置都是经验给定的。Kalnay and Yang(2010)根据前后两次迭代分析误差减小的程度来作为控制迭代次数的依据,这为自动调整迭代次数提供了一个简便的方法,但是在Lorenz96的测试中,通过分析每一步迭代的分析误差可以发现在600个时次的同化中,有相当多时次的同化出现分析误差先增后降的情况,尤其是在预报误差较大的时候,这说明迭代过程并不是一个误差单调下降的过程,仍需要考虑一个更全面的判断标准来决定迭代的次数。此外,当观测时间间隔减小时,传统EnSRF方案的效果迅速提升,iEnSRF的优势将不再明显,而当观测时间间隔更长时,iEnSRF的分析效果也将减弱,与传统方案相当,因此,iEnSRF方案的优势区间是在一个某一个范围内,并不是任何对任意时间间隔的观测都有提升作用。在目前的方案中没有考虑的一点是两个时次间的系统在位相上是有所差别的,对于同一个观测应用的局地化的中心位置(即局地化系数为1的位置)应该是不一样的,但目前还没有针对这一问题提出行之有效的方案,这也是有待研究的问题。
| [1] | Anderson J L,Anderson S L. 1999. A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts [J]. Mon. Wea. Rev.,127(12): 2741-2758. |
| [2] | Anderson J L. 2007a. An adaptive covariance inflation error correction algorithm for ensemble filters [J]. Tellus A,59(2): 210-224. |
| [3] | Anderson J L. 2007b. Exploring the need for localization in ensemble data assimilation using a hierarchical ensemble filter [J]. Physica D: Nonlinear Phenomena,230(1-2): 99-111. |
| [4] | Caya C,Sun J,Snyder C. 2005. A comparison between the 4DVAR and the ensemble Kalman filter techniques for radar data assimilation [J]. Mon. Wea. Rev.,133(11): 3081-3094. |
| [5] | Danforth C M,Kalnay E,Miyoshi T. 2007. Estimating and correcting global weather model error [J]. Mon. Wea. Rev.,135(2): 281-299. |
| [6] | Dee D P,Da Silva A M. 1998. Data assimilation in the presence of forecast bias [J]. Quart. J. Roy. Meteor. Soc.,124(545): 269-295. |
| [7] | Evensen G. 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics [J]. J. Geophys. Res.,99(C5): 10143-10162. |
| [8] | Evensen G. 2003. The ensemble Kalman filter: Theoretical formulation and practical implementation [J]. Ocean Dynamics,53(4): 343-367. |
| [9] | Gao J D,Xue M,Shapiro A,et al. 1999. A variational method for the analysis of three-dimensional wind fields from two Doppler radars [J]. Mon. Wea. Rev.,127(9): 2128-2142. |
| [10] | Gaspari G,Cohn S E. 1999. Construction of correlation functions in two and three dimensions [J]. Quart. J. Roy. Meteorol. Soc.,125(554): 723-757. |
| [11] | Houtekamer P L,Mitchell H L. 1998. Data assimilation using an ensemble Kalman filter technique [J]. Mon. Wea. Rev.,126(3): 796-811. |
| [12] | Houtekamer P L,Mitchell H L. 2001. A sequential ensemble Kalman filter for atmospheric data assimilation [J]. Mon. Wea. Rev.,129(1): 123-137. |
| [13] | Hunt B R,Kalney E,Kostelich J E,et al. 2004. Four-dimensional ensemble Kalman filtering [J]. Tellus A,56(4): 273-277. |
| [14] | Hunt B R,Kostelich E J,Szunyogh I. 2007. Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter [J]. Physica D: Nonlinear Phenomena,230(1-2): 112-126. |
| [15] | Kalnay E,Yang S C. 2010. Accelerating the spin-up of ensemble Kalman filtering [J]. Quart. J. Roy. Meteor. Soc.,136(651): 1644-1651. |
| [16] | Li H,Kalnay E,Miyoshi T. 2009. Simultaneous estimation of covariance inflation and observation errors within an ensemble Kalman filter [J]. Quart. J. Roy. Meteor. Soc.,135(639): 523-533. |
| [17] | Lorenz E N,Emanuel K A. 1998. Optimal sites for supplementary weather observations: Simulation with a small model [J]. J. Atmos. Sci.,55(3): 399-414. |
| [18] | Maybeck P S. 1979. Square root filtering [M].// Stochastic Models,Estimation and Control,Vol. 1. New York: Academic Press,411. |
| [19] | Meng Z Y,Zhang F Q. 2007. Tests of an ensemble Kalman filter for mesoscale and regional-scale data assimilation. Part II: Imperfect model experiments [J]. Mon. Wea. Rev.,135(4): 1403-1423. |
| [20] | Murphy J M. 1988. The impact of ensemble forecasts on predictability [J]. Quart. J. Roy. Meteor. Soc.,114(480): 463-493. |
| [21] | Sakov P,Evensen G.,Bertino L. 2010. Asynchronous data assimilation with the EnKF [J]. Tellus A,62(1): 24-29. |
| [22] | Sun J Z,Crook N A. 1997. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments [J]. J. Atmos. Sci.,54(12): 1642-1661. |
| [23] | Whitaker J S,Hamill T M. 2002. Ensemble data assimilation without perturbed observations [J]. Mon. Wea. Rev.,130(7): 1913-1924. |
| [24] | 许小永,郑国光,刘黎平. 2004. 多普勒雷达资料4DVAR同化反演的模拟研究 [J]. 气象学报,62(4): 410-422. Xu Xiaoyong,Zheng Guoguang,Liu Liping. 2004. Dynamical and microphysical retrieval from simulated Doppler radar observations using the 4DVAR assimilation technique [J]. Acta Meteorologica Sinica(in Chinese),62(4): 410-422. |
| [25] | Xue M,Tong M J,Droegemeier K K. 2006. An OSSE framework based on the ensemble square root Kalman filter for evaluating the impact of data from radar networks on thunderstorm analysis and forecasting [J]. J. Atmos. Oceanic Technol.,23(1): 46-66. |
| [26] | Yang S C,Corazza M,Carrassi A,et al. 2009. Comparison of local ensemble transform Kalman filter,3DVAR,and 4DVAR in a quasigeostrophic model [J]. Mon. Wea. Rev.,137(2): 693-709. |
| [27] | Zhang F,Snyder C,Sun J Z. 2004. Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter [J]. Mon. Wea. Rev.,132(5): 1238-1253. |
| [28] | Zheng F,Zhu J,Zhang R H,et al. 2006. Ensemble hindcasts of SST anomalies in the tropical Pacific using an |
| [29] | intermediate coupled model [J]. Geophys. Res. Lett.,33: L19604,doi: 10.1029/2006GL026994. |
 2012, Vol. 36,
2012, Vol. 36, 

