2. 中国科学院大气物理研究所东亚区域气候—环境重点实验室,北京 100029;
3. 山东省临沂市气象局,临沂 276004
2. Key Laboratory of Regional Climate-Environment Research for Temperate East Asia, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. Linyi Meteorological Bureau of Shandong Province, Linyi 276004
降水的多寡对陆地水循环起着决定性作用,其在时间上的分配变率同样对农业生产和自然生态有很大影响,因而降水成为最重要的天气预报目标量之一。降水预报对防止洪涝灾害的发生具有特别重要的意义,在水文预报应用中经常需要定量降水预报(QPF)。目前,降水预报可通过数值天气预报来获得,预报结果常被作为水文预报系统中的重要参数(Yuan et al., 2007; Amengual et al., 2008; Davolio et al., 2008; He et al., 2009; Xuan et al., 2009)。高预报精度和长预见期是定量降水预报追求的主要目标。然而由于天气动力学系统的混沌特性,预报具有不确定性,因而单一的控制性预报或确定性预报不利于用户在决策中加以应用(Pappenberger et al., 2008)。采用集合预报技术能够获得更好的降水预报(Zhu, 2005; Stensrud and Yussouf, 2007)。
集合预报是估计数值预报中不确定性的一种方法,它将单一确定性预报转变为概率预报(麻巨慧等, 2011)。数值预报中不确定性的一个来源是初始场的不确定性,目前常用为初始场添加扰动的方式来模拟初始场不确定性的概率密度函数,实现扰动集合预报(陈静等, 2005)。导致预报不确定性的另一个源是不同模式采用的不同物理过程,因而通过多模式预报可弥补单一模式的不足。
集合预报的一个目的是可以通过集合预报成员来体现预报结果的不确定性概率密度函数,实现概率预报,即每个预报成员代表了天气状况发生的一种可能。另一个目的是通过集合预报来提高预报可靠性,一般指采用多模式超集合预报,采用择优法(郝世峰等,2011)、加权方法、线性回归、非线性方法及EOF主成分来得到多集合成员的组合预报结果(智协飞等,2009; 段明铿和王盘兴,2006; 林春泽等,2009; 周兵等,2006)。这些研究都表明,多模式集合预报能够提高预报能力。
THORPEX交互式全球预报大集合(简称TIGGE,http://www.wmo.int/pages/prog/arep/wwrp/new/thorpex _new.html [2012–07–21])项目的实施,为广大预报员和应用者提供了一个利用现有业务性全球预报模式发展集合预报及其应用的新基础。目前全球有多个气象预报中心为TIGGE提供了各自的集合预报资料,包括欧洲中期天气预报中心ECMWF、美国气象环境预报中心NCEP、英国气象局UKMO、中国气象局CMA及日本气象厅(Park et al., 2008)。
一些研究表明结合多预报源的超集合预报比单一模式预报更具技巧,但有时事实并非如此(He et al., 2009)。由于来自各预报源的资料之间具有较大差异,因此在考虑采用何种方法结合不同源的资料之前,先行评估各模式的预报能力是有益的(Park et al., 2008)。
目前TIGGE资料的应用研究还处于起步阶段。特别是由于资料量巨大,导致应用者很难简便地提取和处理资料。国内已有一些学者对TIGGE资料的预报能力进行了研究,如Jiao Meiyan(2010)、康志明等(2010)、赵琳娜等(2010)、赵晓琳等(2010)、智协飞和陈雯(2010)。近年来一些研究主要侧重于TIGGE逐日降水预报的应用,如Han et al. (2011)、Yang et al. (2012)、Yan et al. (2012)。但是在很多水文应用中需要更短尺度的降水信息。本文基于中国东部沂沭河流域的逐时降水观测资料,对比分析来自五个中心预报模式的6小时降水预报资料,评估现有全球模式集合预报我国东部季风区流域尺度短期降水的能力。这对于发展该区域多模式集成预报或降尺度预报及其在水文界的应用都将提供有益的认识。
选取的降水数据来自山东省临沂市辖区内的10个主要气象观测站(包括临沂市及所辖9个县的气象站点),这些站点分布在(34.9°N~35.25°N,118.1°E~118.8°E)范围内(图 1)。所在区域为典型的温带季风气候区域,冬半年降水较少,夏半年雨量丰富,降水多集中在6、7、8月,其中8月的降水量在160 mm以上。本研究中选用的降水观测时间序列为2007~2010年7~9月份(共计12个月)内所有的逐小时资料,为便于与TIGGE资料以每6小时为最短预报时间尺度相吻合,将这些观测序列在转化为协调世界时(UTC)后合并为逐6小时序列。为便于和TIGGE资料对比,拟采用10站平均的降水量作为本研究的分析参考资料。通过统计历史上逐6小时降水量(10站平均)的累积直方图,获取对应50%、60%、70%、80%、90%、95%、98%、99%的降水量分位数分别为0.33、0.67、1.4、2.5、5.11、16.71、26.31、37.38 mm,作为TS和BS评分(即Thread评分和Brier评分)的参考阈值。
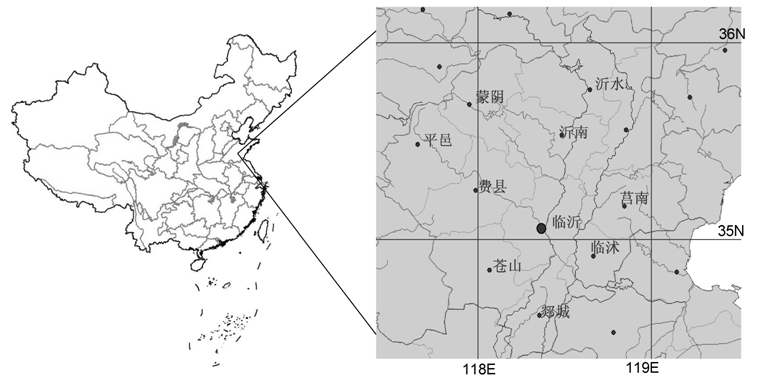 |
图 1 研究区及气象站点分布 Fig.1 The study area and the distribution of meteorological stations |
从TIGGE资料选取来自欧洲中心、英国UKMO、美国NCEP、中国气象局和日本气象厅的五个集合预报系统(EPS)做出的预报,资料代号分别为ECMF(欧洲)、EGRR(英国)、KWBC(NCEP)、BABJ(北京)和RJTD(日本),集合成员数分别为51、24、20、15和50。五种资料具有不同的分辨率,其中ECMF为0.46°×0.46°,KWBC为1°×1°,EGRR为0.8 3°×1.25°(2009年及以前)、0.56°×0.83°(2010年),BABJ为0.56°× 0.56°,RJTD为1.25°×1.25°。由于ECMF成员数较大,分辨率较高,其资料量巨大,在网络获取时采用了0.5°×0.5°分辨率,而其他中心的资料均在下载时保持了原有分辨率。预报时 效除RJTD为36个时次(即整9日)外,其他中心的资料均为40时次(整10日)。
抽取除日本RJTD外的其他资料在2007年7月1日至2010年9月30日间所做的降水预报,每日有2次起报(0000 UTC和1200 UTC),每月共62次起报,预报时效取全部40个时次。因RJTD在一日内只预报一次,即1200 UTC,因此每月31次起报,预报时效取全部36个时次。
不同模式的格点对应不同大小的地区范围,因而用来与观测对比的格点位置可能会影响分析结果。考虑到RJTD资料格点为1.25°分辨率,直接取最接近临沂站的格点值,而其他资料均取(34.5°N~36°N,117.5°E~119°E)范围内多格点的平均值。显然,对不同分辨率的资料难以取得完全相同的格点范围,但经过多次测试表明,最终选定的格点范围对测评指标造成的偏差不影响不同模式的对比和排序。事实上,测试表明对RJTD、KWBC、EGRR等较粗分辨率资料而言,选择单格点和多格点平均对测评结果影响不大,而对ECMF、BABJ等较高分辨率的资料,选择临沂站附近单格点与选择多格点相比,则会对相关系数等指标有较大影响。
用相关系数(R)、均方根误差(RMSE)和Nash效率系数(NE)来定量分析在一个月中每次起报的预报能力波动状况,用以上三种指标及TS和Brier评分评价来自三个不同源的TIGGE集合平均、单个确定性预报和超集合平均的可预报性对比以及预报能力随预见时长的衰减状况。
Nash效率系数(NE),也叫确定性系数,是由Nash and Sutcliffe(1970)提出,公式为
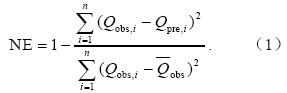
式中,Qobs, i为观测量,Qpre, i为预报量,为观测量均值,n为预报的时段数。NE的范围为-∞~1,越接近于1,表明模拟的效率越高。NE的特点是侧重于对河流洪峰曲线的预报能力评估,也可用来评价在一定预见期内对降水量的预报能力。
TS评分需要使用列联表(Contingency Table),为Sasaki所提出(Sasaki, 1970),它是包含A、B、C、D这4个元素的2×2矩阵。其中A为预报量和观测量均超过了风险阈值的次数,而B为仅预报值超过了风险阈值的次数,C为仅观测量超过了风险阈值的次数,D为预报量和观测量均不超过风险阈值的次数,但TS的计算不需要D值。

TS表征成功预报占总风险预报的百分比,主要用于评估预报事件相对观测事件的一致性程度,其分数范围为0~1,0表示无预报技巧,1为完美评分。
Brier评分(Brier,1950),简写为BS,可用于对概率预报的检验,它是均方根概率误差:
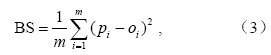
m为预报次数,pi为预报概率,oi为观测概率,对一次事件而言,事件发生为1,不发生为0。BS评分的范围为0~1,完美评分为0,即BS越小,预报准确率越高。
在使用TIGGE预报资料进行预报能力分析之前,首先要验证所提取的资料在时间参考和空间参考上是否与实际相符,这时最好的方法是绘制每次降水预报的曲线,并与实际降水绘制在一起。通过对照可知,资料的提取过程是可靠的。但由于所要考虑的预报较多,实际绘制的图表是3200张以上,但这些图表无法在这里大量列出。只对这些图表效果做简要说明,有以下几点:
(1)各预报中心的资料中各集合预报成员的分布情况有较大不同,其中ECMF各成员较为分散,KWBC的各成员则较为内聚,BABJ各成员的趋势最为散乱,EGRR及RJTD的分散性适中。
(2)与观测对照来看,KWBC、EGRR与RJTD的预报与观测的一致性较好,BABJ表现较差。
(3)所有模式预报降水资料均存在昼夜周期波动现象,其中RJTD、KWBC和EGRR的这种周期十分明显,ECMF则相对较好。
(4)所有模式都不能很好地报出实际降水量。但相对而言,对最近1~2日内的预报都较为可靠,3日后出现较多的误报、漏报、提前、滞后等现象。
图 2中显示了2007年8月12日00时(协调世界时,下同)及8月13日12时所作的四个预报中心的预报结果。从8月12日00时起,4日后发生了连续2日以上的降水。对此,ECMF预报的最好,其次是BABJ,而KWBC似乎完全未报出,而EGRR显示未来会有雨,但预报的降水发生比实际晚了近两天。需要说明的是,本次预报仅属个例,事实上并非每次预报中ECMF都能如此有效,而KWBC的预报也并非总是这样差。在36小时之后的13日12时的预报中(图 2右列),EGRR、ECMF及KWBC对之后2~3天后内发生的连续降水均具有较好的预报能力,ECMF的响应最好,而BABJ对最临近的一日内出现了误报,对2日后发生的降水也有一定的预报能力。这些特征从一定程度上反映了模式集合预报的预报表现。从预报的绝对降水量来看,这些资料对于研究区的预报而言也还差强人意。
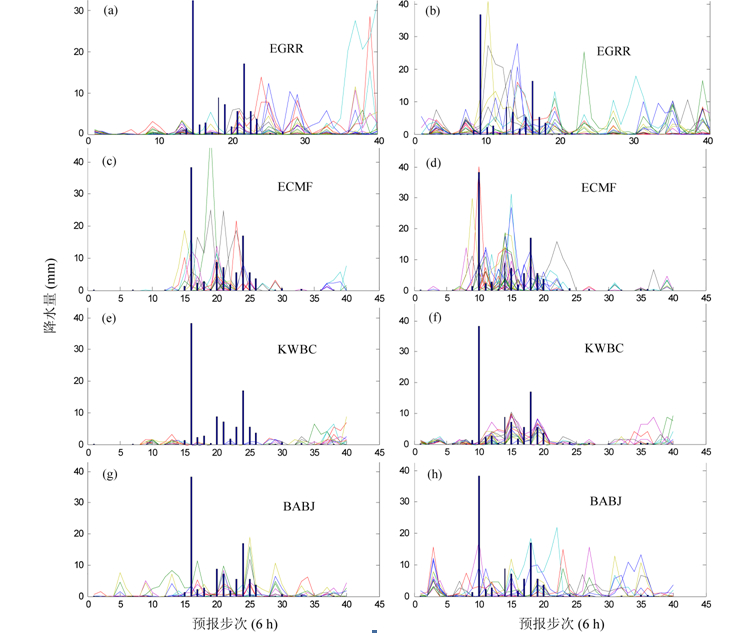 |
图 2 2007年8月12日00时(左列)和13日12时(右列)的两次起报与观测。柱状线表示对应时段内发生的观测降水量,折线表示TIGGE的预报降水量 Fig.2 Two rainfall predictions performed at 0000 UTC 12 Aug (left) and 1200 UTC 13 Aug (right) in 2007. The vertical bars represent the observed precipitation in corresponding period, and the curves represent the predicted precipitation in TIGGE |
用三种量化的方式来对比各EPS的预报能力:①计算每个EPS的单个成员每次起报的降水与观测降水之间的统计量,由于集合成员众多,采用统计量的分布直方图来展示和对比每种集合资料的总体预报能力。统计量采用RMSE和相关系数。②计算每种来自不同预报中心的资料的集合平均,与观测降水量再做RMSE和相关系数的计算,并对单成员控制性预报也做同样的统计计算。③用不同预报中心的集合平均资料,与观测降水量结合来计算不同降水量级别阈值上的TS评分和Brier评分。此外,多模式超集合平均也被用来在第①种方式和第②种方式中参与比较。考虑到各模式成员数相差较大,若采用多模式所有成员全部参与超集合平均的计算将会导致ECMF获得过大的权重,这里采用将各模式的集合分别计算平均后,再用这些各模式的平均代表各模式预报结果,以等权重参与多模式平均。
这里将单个集合成员的降水预报与观测之间都做统计量的计算,最后计算考虑所有预报和所有成员的总平均,以实现多个预报系统的预报能力对比。只取每次预报的前16个时次(即4日内预见期)的预报降水量与观测降水量实现定量指标的计算。选前4日的预见期,是因为通过观测对比证实,ECMF等TIGGE资料在4日的预见期具有一定预报能力。若选取时次更多,则后续的较差时次可能会干扰对前面预报较好时次的评价。但若选取时次更短,则RMSE及相关系数的计算将因样本量过少而失去统计意义。这里的统计量只考虑相关系数和RMSE。总平均统计量的计算如下:
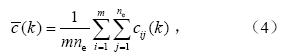
其中为第k个预报中心的统计量总平均,ne为成员数,cij(k) 为第k个预报中心在第i次预报中第j个集合成员的预报降水序列与观测降水二者计算的统计量,该统计量为相关系数、RMSE。
图 3列出了5个预报中心的RMSE和相关系数的对比状况。可见,无论是只取前16时次,还是考虑36时次,EGRR的相关系数最高,往后依次是KWBC、ECMF、RJTD和BABJ。而从RMSE来看,表现最好的是KWBC,往后依次是EGRR、RJTD、ECMF和BABJ。这种单成员的分析能从一定程度上体现不同模式所有成员所有起报的总体差异。
 |
图 3 各中心资料扰动集合成员预报与观测降水的(a)相关系数和(b)RMSE Fig.3 Histograms of (a) correlation coefficients and (b) RMSE between observed rainfall and each disturbed ensemble member in the three TIGGE data archives |
分别用四种不同的预报资料与观测降水相结合来计算统计量:一是取各中心的集合平均降水;二是取各中心发布的确定性预报降水;三是使用各模式集合平均的多模式再平均;四是只用单个模式的控制性预报成员。与前面计算单成员的统计量只针对每次预报降水序列不同,这里是将各个模式获得的预报集合平均量序列的多次预报拼接起来,构成一个向量,长度为
L = l×a×nm,
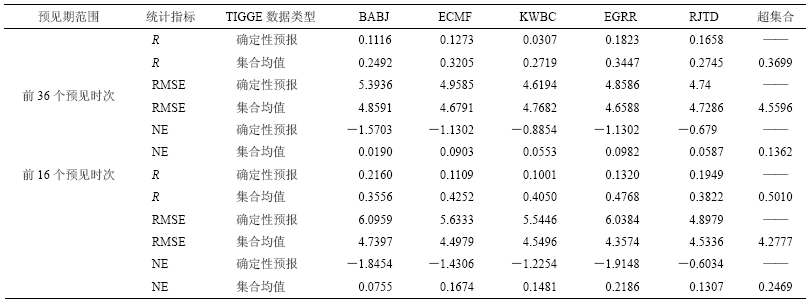
其中,l为所考虑的每次预报的预见时次;a为每月中的预报次数,如ECMF每月预报60次或62次;nm为总月数,即4年共12个月。对应的观测降水序列也采用同样的方法拼接为一个向量。要计算的统计量为相关系数、RMSE及Nash效率系数,计算时l 取前36个预见时次(相当于9天预见期)和前16个预见时次(4天预见期),结果见表 1。
| 表 1 各中心资料集合预报均值与观测值之间的统计量 Table 1 Statistics between observed rainfall and ensemble means of different EPSs |
从集合平均来看,前16时次中EGRR的相关系数最大,达0.48,往后是ECMF和KWBC,分别为0.425和0.405,RJTD的相关系数为0.38,而BABJ只有0.36;RMSE与Nash系数也表现了相同的排列顺序。前36时次中,EGRR的相关系数最大,为0.34,往后依次是ECMF(0.32)、RJTD(0.27)、KWBC(0.27)、BABJ(0.24);RMSE的排列顺序是EGRR(4.65)、ECMF(4.67)、RJTD(4.73)、KWBC(4.77)、BABJ(4.86),Nash系数的排列顺序是EGRR(0.10)、ECMF(0.09)、RJTD(0.06)、KWBC(0.05)和BABJ(0.02)。可见三个指标的排列顺序完全相同。
从确定性的控制预报来看,前16时次中,BABJ的相关系数最大,达0.22,RJTD其次,为0.19,其后是EGRR(0.13)、ECMF(0.11)和 KWBC(0.1);从RMSE来看,RJTD最小,为4.9,往后依次为KWBC、ECMF、EGRR和BABJ;Nash系数最高的是RJTD(-0.6),往后是KWBC(-1.23)、ECMF(-1.43)、BABJ(-1.84)、EGRR(-1.91)。在前36时次中,相关系数的排列为EGRR(0.18)、RJTD(0.166)、ECMF(0.13)、BABJ(0.11)和KWBC(0.03)。对RMSE和Nash系数而言,排列顺序为EGRR、ECMF、KWBC、RJTD和BABJ。显然,只从4日预见期来看,BABJ、RJTD及 KWBC的表现较好,但从9日预见期来看,EGRR表现最好。
从多模式集合预报效果来看,其三个指标均远超过任何一个单模式,如对前16个时次,相关系数达0.50,高于表现最好的EGRR(0.48),RMSE为4.28,低于表现最好的EGRR(4.35),Nash系数为0.25,高于表现最好的EGRR(0.22)。
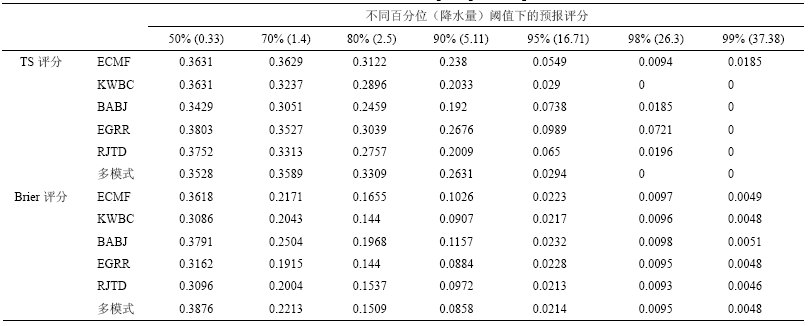
针对前16个时次的预见期,计算了单模式集合平均及多模式集合平均的TS评分和Brier评分(表 2)。随着降水阈值的提高,单模式集合平均的TS评分和Brier评分基本呈快速下降趋势。对0.9以上的分位数阈值,TS评分全为0,对0.98的分位数阈值,Brier评分全为0。
| 表 2 集合平均降水预报的TS评分与Brier评分 Table 2 The threat scores and Brier scores of the precipitation prediction of ensemble means |
(1)单模式集合平均降水预报的评分。将每 个模式的集合预报平均降水量作为评价对象,来体现多成员平均值的预报能力。在多个阈值上EGRR获得的TS评分均最高,其次为ECMF、KWBC、RJTD。BABJ对0.7及以下的分位数阈值上,获得的TS评分为最低,但对0.8分位数阈值,其TS评分仅次于EGRR。同时,对0.5的分位数阈值而言,EGRR获得的Brier评分值最低(即预报效果最好),其次为RJTD、KWBC、ECMF和BABJ。对0.8分位数阈值而言,RJTD及KWBC的Brier评分最优,BABJ和EGRR其次,最差的是ECMF,但总体上五个模式相差不大。对ECMF、KWBC、BABJ、EGRR四模式的超集合平均,在0.5百分位阈值上其TS评分最大,但在其他百分位阈值上均不占优势,且在0.8百分位上其评分最小。显然,集合平均使预报极值降低造成了超集合平均主要在较高百分位阈值上TS评分的降低。
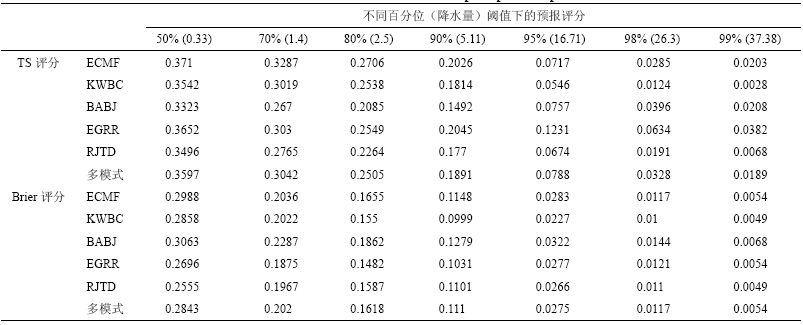
(2)考虑所有单成员预报的评分。是将每个成员对降水的预报进行TS及BS评分的统计计算,评价单个成员的集合预报能力,结果见表 3。在0.5分位数阈值上,ECMF的TS评分最高,其次为KWBC等其他三个成员,BABJ表现最差。在0.6、0.7和0.8的分位数阈值上,EGRR的TS评分均最高,其次为KWBC等三个成员。BABJ在前三个阈值上仍表现较差,但在0.8分位数阈值下表现优于除EGRR外的任何成员。对Brier评分,在0.5和0.6分位数阈值下,EGRR均表现最优,但在0.7和0.8分位阈值下时,KWBC表现最优。BABJ在任何阈值下都表现最差。对多模式超集合而言,无论是TS还是Brier评分,在低阈值上的评分都表现接近最优,但对0.7以上分位数阈值,评分不再占优。经对比可知在低阈值上,集合平均的预报TS高得多,如超集合平均预报的TS为0.30,而超集合的所有成员预报的TS为0.31;但在高阈值上,集合平均的预报TS则低得多。同样,BS具有类似的效果。可见,超集合平均由于忽略了成员的分散性,从而降低了对极值降水的预报。
| 表 3 考虑所有集合成员的降水预报的TS评分与Brier评分 Table 3 The mean threat scores and Brier scores from the precipitation prediction of all ensemble members |
为了验证各中心资料集合平均的预报能力衰减状况,在整个预见期(40时次)上开一个宽度为5时次的滑动窗,窗口向前滑动时每步移动一个时次(即6 h),使所有集合预报平均序列位于同一窗内的部分抽出并拼接在同一向量中,将其与观测降水对比,计算相关系数、RMSE、NE、TS评分以及BS。
由图 4中可见,三种集合预报的相关系数及NE总体随预报时效的后延而呈下降趋势,RMSE则呈增大趋势。就相关系数和NE而言,KWBC和EGRR在一日内预见期时表现最优,但在第二日、三日内KWBC的衰减很快,而EGRR的衰减较为缓慢,其预报效果最优。至第二、三日时,ECMF因衰减缓慢,其预报效果只逊于EGRR。在第5日后ECMF的相关系数及NE为最高,而EGRR由于衰减较快,其优势不再明显。BABJ在大部分预见期内其表现是最差的。各模式的RMSE均表现出昼夜周期波动性,这表明它对预报结果中的昼夜周期性较为敏感。但由RMSE得到的各模式预报能力对比情况与由其他指标获得的结果较为一致。对四模式集合平均预报而言,在绝大部分预见期内的表现都明显优于单模式集合平均预报。从4日内的预报效果来看,各集合预报的排列顺序是多模式超集合—KWBC—RJTD—ECMF—BABJ。
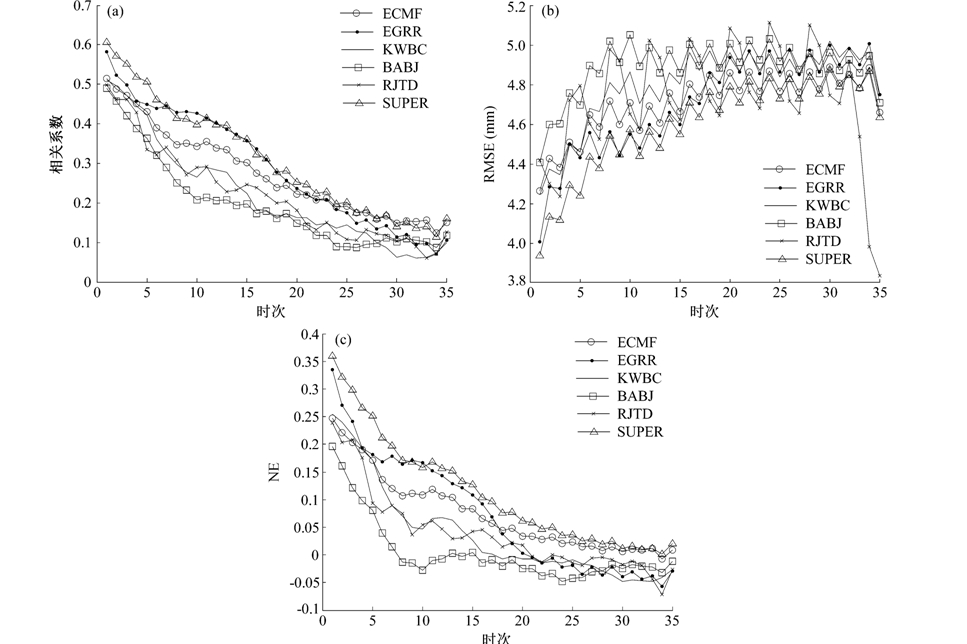 |
图 4 滑动预报时效下五种资料的集合降水预报平均与观测值间的相关系数、RMSE及NE Fig.4 The correlation coefficients, RMSE, and NE obtained from the TIGGE archives with different lead times. The statistics were calculated by extracting data from a smoothed window at different lead times |
从相关系数和NE衰减所用的时间来看,BABJ和RJTD均在96小时(第24时次)左右衰减至随机态,而其他模式及多模式平均则稳定衰减直至第34个时次(136小时)。按照衡量定量预报的RMSE来看,大部分模式的定量预报能力可持续到3~4天,实际上在第3日内RMSE与随机态相差不大了。图 4b显示RJTD的RMSE曲线在尾部快速下降,这因为在35时次之后RJTD已无数据,但仍用5时 次跨度滑动计算RMSE,在资料长度越来越短时造成RMSE计算值趋小,而其他资料的预报时次数达40小时,因此计算结果正常。
由图 5可见,随着预见期的增加,所有模式的预报能力均呈现明显的下降趋势, 即TS明显降低,而BS呈增加趋势。 但对5.1 mm以上的降水阈值,BABJ与ECMF的BS下降幅度已很小,这说明BS评分的敏感性较差,难以体现不同模式的预报能力差异。在5.1 mm阈值上,超集合平均的BS呈现最小,说明这时其预报能力强于任何单模式,而它在其他较小阈值上的BS不是最小的,这说明超集合平均的计算处理会使对小降水的预报能力降低。
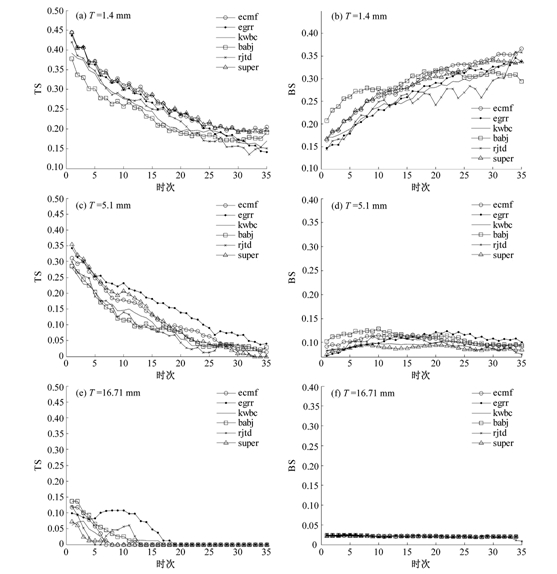 |
图 5 集合降水预报平均及超集合平均(SUPER)与观测值间的加窗滑动TS评分(左)及Brier评分(右) Fig.5 Threat scores (left) and Brier scores (right) obtained from ensemble means of KWBC, ECMF, EGRR, BABJ, RJTD and the super grand ensemble mean |
从5.1 mm以下的阈值而言,ECMF、EGRR及多模式平均的TS基本上在整个预见期内呈稳定下降趋势,而BABJ、RJTD、KWBC均在96小时(24个时次)的预见期内是稳定下降的,96小时后虽仍在下降,但较接近随机状态。其中EGRR在整个预见期内及不同阈值上的预报能力一直领先,其次为ECMF。而超集合平均的预报能力在较小阈值上与EGRR接近,而在中等阈值上表现适中,在较大阈值上表现最差。这显然是因为超集合平均使其对极值的预报能力显著降低了。
而对16.71的阈值,EGRR的稳定下降趋势或预报能力仍能保持至16时次左右,而多模式平均及除EGRR之外的其他模式预报在2~3日预见期内的TS下降至零,存在一定上升波动,但总体仍呈下降趋势。TS的上升波动主要是由于缺少较大降水量的样本从而使随机因素占了很大比例所造成。
不同模式可能存在着预报的系统性偏差,体现在所有集成成员上。为了弄清TIGGE资料中这些模式的系统性偏差,采用了分别计算观测降水和所有EPS预报降水的分位数实现对比。降水的百分位从0.01起,按0.02为间隔选取,即所有降水的百分位在0.01~0.99范围内。这里EPS预报降水的分位数是指考虑所有集合成员所有预报的分位数,而非集合均值的分位数。观测与预报降水的分位数对比如图 6。可见,按预报偏差从小到大的排序为BABJ,EGRR、RJTD、ECMF和KWBC。由于预报偏差与前述几种预报能力评价并不直接关联,因而预报能力较差的BABJ资料却具有最小的预报偏差。
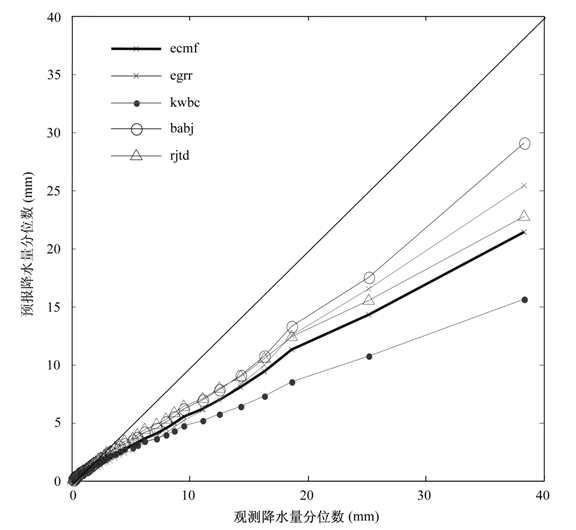 |
图 6 观测降水与所有模式预报降水的分位数对比 Fig.6 Comparison of precipitation quantile of all EPS predictions to the observed precipitation |
总的来看,观测与预报降水分位数的对比基本 近似于直线分布,因此五种资料拟合的回归方程为:

由图可见,这些方程大约在EPS预报降水量大于 3 mm时适用。
这种系统性偏差可能会影响前述各种评价指标的计算,从而不能真正体现各模式的应用潜力对比。但这种偏差带来的影响并不显著,是由以下原因决定的:一是五个模式只是对较大降水量(>3 mm)的预报存在显著不同的偏差,而模式预报中3 mm已大于0.8的分位数,即绝大部分为微量降水;二是各EPS对较大降水的定量预报能力又都比较差,且样本量较少,对上述评价指标的影响是有限的。
本文基于BABJ、ECMF、EGRR、RJTD和KWBC五种TIGGE资料,以我国东部沂沭河流域为例,对6小时降水的预报水平进行了详细评估,得出如下结论:
(1)从所有预报成员的单次预报的平均相关系数和RMSE来看,KWBC表现最好,EGRR、ECMF、RJTD预报能力相当,BABJ表现最差。但KWBC的指标明显优于其他资料的一个原因可能是其成员不够发散,导致其较低的指标出现较少。
(2)如果将每个EPS的集合平均作为预报结果,EGRR占有明显优势,ECMF次优,RJTD略优于KWBC,而BABJ表现最差。从4日内的预见期来看,EGRR的相关系数能达到0.48,Nash系数为0.22。从4日内的确定性控制预报来看,BABJ表现最优,相关系数为0.22,RJTD次优,相关系数为0.19,Nash系数为负值。其次为EGRR和KWBC。这个结果与集合预报相比有很大差异,但与临沂气象局近年来常参考日本和中国的模式进行天气预报的事实较为吻合。
(3)就控制性预报而言,对任何一个EPS,其集合平均的统计指标占绝对优势;同样,多模式(或称多EPS)集合平均作为预报结果时,其统计指标比任何一个单模式集合平均也有绝对优势。在4日预见期内,相关系数可达0.50,Nash系数为0.25。
(4)在0.5分位数阈值(3.3 mm)下,对于集合平均作为降水预报,多模式集合平均表现最好(TS为0.3)。单模式中EGRR表现最好(TS也为0.3),其次是ECMF、KWBC和RJTD;但对0.8分位数阈值(25 mm)下,RJTD和BABJ的表现优于其他资料。不过由于本研究所用数据中较高阈值的降水发生频次较低,因而BABJ对较大降水的预报能力是否适中仍值得怀疑。
(5)若用所有集合成员作为概率预报的依据,在0.5分位数阈值上按TS评分,ECMF表现最好,其次为KWBC和EGRR;而在0.6、0.7和0.8分位数阈值上EGRR表现最好。BABJ在0.8分位数阈值上表现较好。但按BS评分来看,在多个阈值上EGRR和KWBC最优,BABJ表现最差。多模式总概率预报的TS和BS评分在低阈值下接近最优,但其他 阈值下不占优势。这是因为这种总概率预报只提供了更多的可能性,但不能加强某种预报可能的发 生概率,这与多模式平均或加权预报本质上有很大不同。
(6)从各中心预报随预报时效长度的衰减状况来看,各中心资料均具有一个稳定的衰减期,其中EGRR衰减期最长且最为稳定,其衰减能持续9天左右,而其他资料则具有不同程度的稳定衰减,稳定衰减期都能持续4天以上。
总的来看,各预报系统(或模式)的集合预报中,EGRR预报能力最高,ECMF、KWBC、RJTD各有千秋,而BABJ预报能力最低。只从控制预报来看,RJTD和BABJ对研究区的预报能力最好。而任何模式的集合预报能力又都优于其控制预报,多模式平均预报又优于单一模式,且都具有明显的预报能力提升。由此可以得出一个推论,当将更多的模式结果作为集合预报的参考时,最终的集合平均预报能力则会更优。
从目前的降水定量预报实际来看,各中心模式仍与理想相差甚远。但即便如此,通过RMSE分析表明,由相关系数及Nash等统计量较大的模式或集合平均预报确实具有较小的RMSE值。
| [1] | Amengual A, Diomede T, Marsigli C, et al. 2008. A hydrometeorological model intercomparison as a tool to quantify the forecast uncertainty in a medium size basin [J]. Natural Hazards and Earth System Sciences, 8 (4): 819-838. |
| [2] | Brier G W. 1950. Verification of forecasts expressed in terms of probability [J]. Mon. Wea. Rev., 78 (1): 1-3. |
| [3] | 陈静, 薛纪善, 颜宏. 2005. 一种新型的中尺度暴雨集合预报初值扰动方法研究 [J]. 大气科学, 29 (5): 717-726. Chen Jing, Xue Jishan, Yan Hong. 2005. A new initial perturbation method of ensemble mesoscale heavy rain prediction [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 29 (5): 717-726. |
| [4] | Davolio S, Miglietta M M, Diomede T, et al. 2008. A meteo-hydrological prediction system based on a multi-model approach for precipitation forecasting [J]. Natural Hazards and Earth System Sciences, 8 (1): 143-159. |
| [5] | 段明铿, 王盘兴. 2006. 一种新的集合预报权重平均方法 [J]. 应用气象学报, 17 (4): 488-493. Duan Mingkeng, Wang Panxing. 2006. A new weighted average method on ensemble mean forecasting [J]. Journal of Applied Meteorological Science (in Chinese), 17 (4): 488-493. |
| [6] | 郝世峰, 潘劲松, 李冲, 等. 2011. 择优法降水集合预报试验的研究 [J]. 热带气象学报, 27 (3): 336-344. Hao Shifeng, Pan Jinsong, Li Chong, et al. 2011. Ensemble prediction experiments on precipitation by using optimization method [J]. Journal of Tropical Meteorology (in Chinese), 27 (3): 336-344. |
| [7] | Han J, Ye Q, Yan Z W, et al. 2011. Conceptual study on incorporating user information into forecasting systems [J]. Frontiers of Environmental Science & Engineering in China, 5 (4): 533-542. |
| [8] | He Y, Wetterhall F, Cloke H L, et al. 2009. Tracking the uncertainty in flood alerts driven by grand ensemble weather predictions [J]. Meteorological Applications, 16 (1): 91-101. |
| [9] | Jiao Meiyan. 2010. Progress on the key technology development in application of ensemble prediction products associated with TIGGE [J]. Acta Meteorologica Sinica, 24 (1): 136. |
| [10] | 康志明, 金荣花, 鲍媛媛, 等. 2010. 基于TIGGE数据的我国寒潮自动识别预报方法 [J]. 应用气象学报, 21 (3): 298-306. Kang Zhiming, Jin Ronghua, Bao Yuanyuan, et al. 2010. Automatic identification forecast for cold wave in China based on TIGGE ensemble data [J]. Journal of Applied Meteorological Science (in Chinese), 21 (3): 298-306. |
| [11] | 林春泽, 智协飞, 韩艳, 等. 2009. 基于TIGGE资料的地面气温多模式超级集合预报 [J]. 应用气象学报, 20 (6): 706-712. Lin Chunze, Zhi Xiefei, Han Yan, et al. 2009. Multi-model superensemble forecasts of the surface temperature using the TIGGE data [J]. Journal of Applied Meteorological Science (in Chinese), 20 (6): 706-712. |
| [12] | 麻巨慧, 朱跃建, 王盘兴, 等. 2011. NCEP、ECMWF及CMC全球集合预报业务系统发展综述 [J]. 大气科学学报, 34 (3): 370-380. Ma Juhui, Zhu Yuejian, Wang Panxing, et al. 2011. A review on the developments of NCEP, ECMWF and CMC global ensemble forecast system [J]. Transactions of Atmospheric Sciences (in Chinese), 34 (3): 370-380. |
| [13] | Nash J E, Sutcliffe J V. 1970. River flow forecasting through conceptual models. Part I—A discussion of principles [J]. J. Hydrol., 10 (3): 282- 290. |
| [14] | Pappenberger F, Bartholmes J, Thielen J, et al. 2008. New dimensions in early flood warning across the globe using grand-ensemble weather predictions [J]. Geophys. Res. Lett., 35(10): L10404, doi:10.1029/ 2008GL033837. |
| [15] | Park Y Y, Buizza R, Leutbecher M. 2008. TIGGE: Preliminary results on comparing and combining ensembles [J]. Quart. J. Roy. Meteor. Soc., 134 (637): 2029-2050. |
| [16] | Sasaki Y. 1970. Some basic formalisms in numerical variational analysis [J]. Mon. Wea. Rev., 98 (12): 875-883. |
| [17] | Stensrud D J, Yussouf N. 2007. Reliable probabilistic quantitative precipitation forecasts from a short-range ensemble forecasting system [J]. Wea. Forecasting, 22 (1): 3-17. |
| [18] | Xia J J, Han J R, Yan Z W, et al. 2009. User-oriented evaluation of summer rainfall forecast in the Huaihe basin, eastern China, based on TIGGE products [C]// Proceedings of the 2nd THORPEX-ASIA Science Workshop. Hangzhou. |
| [19] | Xuan Y, Cluckie I D, Wang Y. 2009. Uncertainty analysis of hydrological ensemble forecasts in a distributed model utilising short-range rainfall prediction [J]. Hydrology and Earth System Sciences, 13 (3): 293-303. |
| [20] | Yan Z W, Han J R, Jiao M Y, et al. 2012. Formation of an interactive user-oriented forecasting system-experience from hydrological application in Linyi, eastern China [J]. Acta Meteorologica Sinica, 26 (1): 13-25. |
| [21] | Yang C, Yan Z W, Shao Y H. 2012. Probabilistic precipitation forecasting based on ensemble output using generalized additive models and Bayesian model averaging [J]. Acta Meteorologica Sinica, 26 (1): 1-12. |
| [22] | Yuan H L, Gao X G, Mullen, S L, et al. 2007. Calibration of probabilistic quantitative precipitation forecasts with an artificial neural network [J]. Wea. Forecasting, 22 (6): 1287-1303. |
| [23] | 赵琳娜, 吴昊, 田付友, 等. 2010. 基于TIGGE资料的流域概率性降水预报评估 [J]. 气象, 36 (7): 133-142. Zhao Linna, Wu Hao, Tian Fuyou, et al. 2010. Assessment of probabilistic precipitation forecasts for the Huaihe basin using TIGGE data [J]. Meteorological Monthly (in Chinese), 36 (7): 133-142. |
| [24] | 赵晓琳, 朱国富, 李泽椿. 2010. 基于TIGGE资料识别适应性观测敏感区的应用研究 [J]. 应用气象学报, 21 (4): 405-415. Zhao Xiaolin, Zhu Guofu, Li Zechun. 2010. Applied research on adaptive observation for identifying sensitive regions based upon TIGGE data [J]. Journal of Applied Meteorological Science (in Chinese), 21 (4): 405-415. |
| [25] | 智协飞, 陈雯. 2010. THORPEX国际科学研究新进展 [J]. 大气科学学报, 33 (4): 504-511. Zhi Xiefei, Chen Wen. 2010. New achievements of international atmospheric research in THORPEX program [J]. Transactions of Atmospheric Sciences (in Chinese), 33 (4): 504-511. |
| [26] | 智协飞, 林春泽, 白永清, 等. 2009. 北半球中纬度地区地面气温的超级集合预报 [J]. 气象科学, 29 (5): 569-574. Zhi Xiefei, Lin Chunze, Bai Yongqing, et al. 2009. Superensemble forecasts of the surface temperature in Northern Hemisphere middle latitudes [J]. Scientia Meteorologica Sinica (in Chinese), 29 (5): 569-574. |
| [27] | 周兵, 赵翠光, 赵声蓉. 2006. 多模式集合预报技术及其分析与检验 [J]. 应用气象学报, 17 (S1): 104-109. Zhou Bing, Zhao Cuiguang, Zhao Shengrong. 2006. Multi-model ensemble forecast technology with analysis and verification of the results [J]. Journal of Applied Meteorological Science (in Chinese), 17 (S1): 104-109. |
| [28] | Zhu Y J. 2005. Ensemble forecast: A new approach to uncertainty and predictability [J]. Advances in Atmospheric Sciences, 22 (6): 781-788. |
 2013, Vol.
2013, Vol.