2. 南京信息工程大学大气科学学院,南京 210044;
3. 上海市气象信息传媒中心,上海 200030
2. Nanjing University of Information Science and Technology, Nanjing 210044;
3. Shanghai Weather Information Media Center, Shanghai 200030
研究表明,自工业革命以来,大气中温室气体的含量大大增加,对大气组成、辐射强迫和全球气候变化都具有重要影响,而且对全球气候变暖有主要贡献。为了减缓全球增暖,必须限制这些温室气体的排放量。因此,二氧化碳(CO2)、甲烷(CH4)、氧化亚氮(N2O)和卤化碳等长寿命温室气体,均被列入《京都议定书》中要求控制它们的排放量。
作为主要的温室气体,CH4、N2O具有大气含量较高、受人类活动影响大,气体分子辐射吸收能力较强,大气寿命较长等特性。首先,CO2、CH4和N2O的大气含量在均匀混合的温室气体中居于前三位(非均匀混合的水汽和臭氧除外),并且造成它们浓度增加的主要因素均为人类活动的影响。大气中CH4浓度与人类活动密切相关,60%的排放来自人类活动,其浓度值在工业化前约715 ppb(IPCC,2007),到2008年CH4的全球平均体积混合率已经达到1797 ppb(1 ppb=10-9)(WMO,2009),近年来仍有明显增加;全球大气中N2O的增加也主要受到人类活动影响,浓度值已从工业化前约270 ppb(IPCC,2007),增加到2008年的321.8 ppb(WMO,2009)。其次,CH4和N2O是地球大气的主要吸收气体,分别在7.8 µm、3.3 µm和17 µm等多个谱带有吸收,并在7.8 µm二者有重要的重叠吸收,因而改变了这些光谱区域大气的吸收性质,对地气系统向外空的辐射冷却产生很大的影响。再者,CH4和N2O都具有较长的大气寿命,即:在自然过程把排放到大气中的这些温室气体清除之前,它们将在大气中存留至少十几年甚至上百年,在此期间,它们累积在大气中,对影响大气辐射平衡和全球气候产生持续的贡献。
随着全球变暖的加剧,已有愈来愈多的国内外学者关注CH4、N2O,除了它们的源排放和在大气中含量的变化,定量评估它们对地球辐射平衡和气候产生的影响已经成为气候变化研究中的热点。这是因为,制定具体可行的温室气体减排政策,并为相关决策提供科学依据,要求定量地评估温室气体的气候效应,即用一定的标准来衡量不同温室气体对未来全球气候变暖的相对贡献。目前,对温室气体的气候效应采用的评估方法,主要包括辐射强迫、全球增温潜能(GWP)和全球温变潜能(GTP)等工具。Zhang et al.(2011)和张华等(2011)用高光谱分辨率的辐射传输模式分别研究了《京都议定书》限制排放的痕量温室气体HFCs、PFCs和SF6的辐射强迫和全球增温潜能,但是没有研究《京都议定书》限制排放的CH4、N2O等主要温室气体。Shine et al.(2005)、Fuglestvedt et al.(2003)、石广玉(1991,2007)、Shi(1981)、黄兴友(2001)等学者在这方面做了很多工作,但与现在的条件相比,模式所用谱线资料不够新,辐射模式的精确性也有待提高。因此,用新的气体吸收资料、更精确的辐射计算模式和新的评估方法(GTP)来研究CH4、N2O等《京都议定书》限排气体是十分必要的。
本文在前人工作的基础上,利用HITRAN2K发布的分子吸收资料和高精度的辐射传输模式,首先计算了CH4、N2O的瞬时辐射效率和平流层调整的辐射效率,并考虑了大气寿命对辐射效率的影响;其次,根据不同浓度下产生的辐射强迫值,拟合了简单的气体辐射强迫计算公式,以易于评估未来气体浓度增加对全球变暖的影响;最后,计算了它们在未来10~500年的GWP和GTP,并对两种不同的排放测量方法进行了比较。
2 资料与模式介绍 2.1 HITRAN资料
为了准确地研究气体的温室效应,进行精确的特别是高光谱分辨率的辐射计算,需要输入大气分子吸收谱线的资料。本文采用的HITRAN(HIgh- resolution TRANsmission,高分辨透过率)分子光谱数据库(Rothman et al.,2005),是国际科学界公认且广泛应用于大气辐射传输计算的基础资料,本文所用版本是HITRAN2K。HITRAN2K分子光谱数据库既收录了H2O、CO2、CH4、N2O、O3等大气中主要气体的各项谱线参数,也给出了臭氧消耗物质CFCs和HCFCs,及其代替品HFCs、PFCs和SF6等诸多化合物的红外吸收截面数据,是本文研究的基础。Lu et al.(2012)证明了HITRAN2K版本的CH4和N2O的总线强与目前释放的最新版本HITRAN08基本一致,没有太大变化,因此分子光谱数据的变化不会对本文的计算产生影响。
2.2 辐射传输模式
本文采用的是Zhang et al.(2003,2006a,2006b)研制的长波辐射传输方案。该模式是基于Zhang et al.(2003)利用LBLRTM计算得到的大气主要温室气体和CFCs的吸收系数,根据Shi(1981)提出的相关k-分布吸收系数重排法,Zhang et al.(2003)提出的气体吸收带重叠优化方法,Zhang et al.(2006a)提出的k-分布间隔的选取方法,以及Zhang et al.(2006b)的谱带划分方法建立起来的。Zhang et al.(2006a)的辐射计算方案 将长波区间分为17、21、27、55、998等不同的谱带,同时考虑了云的作用。在长波区间云的吸收与发射算法采用了Nakajima et al.(2000)的计算方法。Zhang et al.(2006b)给出的高精度的998带辐射传输方案则是将光谱区间10~49000 cm-1(0.2~1000 µm)划分为998个带,长波区间10~2500 cm-1(4~1000 µm)分为498个带,每个带的波段区间均为5 cm-1,k-间隔数量对于每个带都进行了优化,2~16不等,具体谱带划分、k -间隔数量以及吸收气体分布见Zhang et al.(2006b)。张华等(2011)证明了利用998带辐射传输方案计算温室气体的辐射强迫和全球增温潜能比利用为气候模式设计的17带方案要精确得多,故本文采用998带辐射传输方案进行研究。
该辐射模式中考虑了大气中15种温室气体,包括5种主要温室气体:H2O、CO2、O3、CH4和N2O,和CFCs、HFCs、PFCs等10种痕量化合物,并假设这些痕量气体在大气中混合均匀。CH4主要在第105~124带、第239~278带和第424~498带有吸收。可见,高光谱精度的998带辐射方案由于谱带划分较细,k-间隔数量多,在计算可以更全面地考虑气体的强弱带吸收(Zhang et al.,2011)。
此外,模式将整层大气分为100层,垂直分辨率为1 km,地面高度设为0 km,大气顶取为70 km。对辐射通量和加热率的计算,采用六种模式大气(Gar and ,2001):热带大气(TRO),中纬度夏季大气(MLS),中纬度冬季大气(MLW),亚极夏季大气(SAS),亚极冬季大气(SAW)和美国标准大气(USS)。在此基础上,计算目标气体在六种大气下的瞬时辐射效率和平流层调整的辐射效率,并通过对六种模式大气的结果取算术等权平均和其中3种大气取区域加权平均,可以认为得到全球平均结果。
3 CH4、N2O的辐射强迫 3.1 定义与计算方案
辐射强迫是目前应用广泛的一种评估温室气体气候效应相对大小的方法,定义为某种辐射强迫因子(如温室气体的浓度)变化时所造成的对流层顶净辐射通量的变化。IPCC(1996)按照是否允许平流层温度进行调整,将辐射强迫划分为两种:①瞬时辐射强迫(IRF,Instantaneous Radiative Forcing),不考虑平流层温度变化;②调整过的辐射强迫(ARF,Adjusted Radiative Forcing),即,在保持地表和对流层温度不变的情况下,通过调整平流层的温度结构,使平流层达到辐射平衡时,对流层顶的净辐射通量的变化。根据定义,辐射强迫可以提示气候变化的总趋势,一般而言,正的辐射强迫将增暖地面和对流层,使全球变暖,引起地表平均温度升高;负的辐射强迫使地面和对流层变冷,引起地表平均温度降低。因此,可以通过计算CH4和N2O的辐射强迫来估量在它们在大气中的浓度变化对气候系统产生的影响。
本文采用了Zhang et al.(2011),张华等(2011)的迭代法来计算平流层调整的辐射强迫,如图 1所示。图中ε为收敛值,Δt为迭代的时间步长,单位为d,本文取为1 d。如果满足收敛条件,即可认为平流层经过温度调整达到了新的辐射平衡,此 时所得到的对流层顶净辐射变化即该气体的调 整辐射强迫。如果引起气候系统扰动的气体浓度为单位浓度,如1 ppm或1 ppb,则对应的辐射强 迫称为该气体的辐射效率(本文中单位统一为 W m-2 ppb-1)。
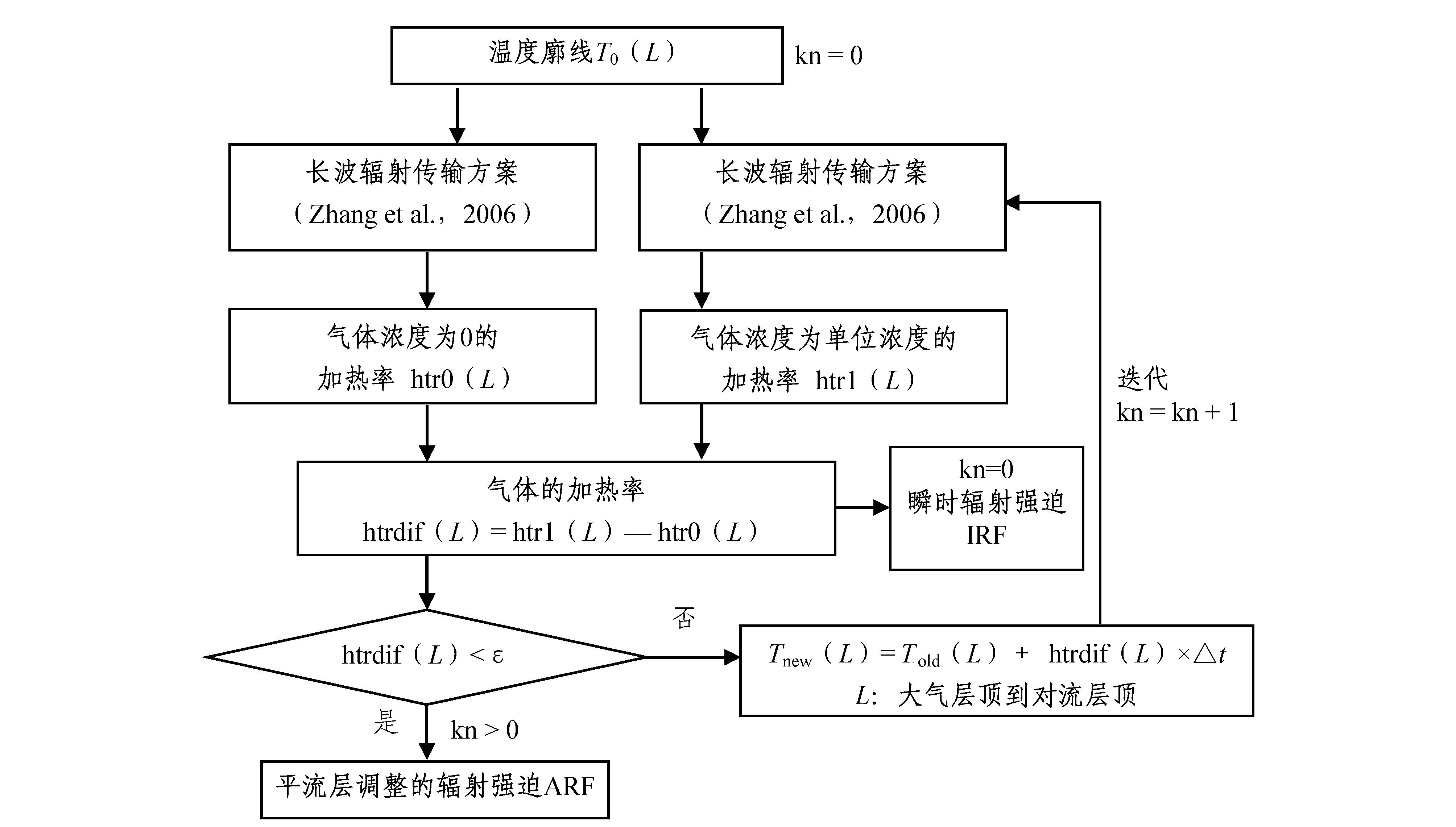 | 图 1 计算温室气体平流层调整的辐射强迫的迭代方法(引自Zhang et al., 2011)Fig. 1 Schematic of iterative method to compute the stratospheric adjusted radiative forcing of GHG (Greenhouse Gas) (from Zhang et al., 2011) |
云是影响气体辐射强迫的一个重要因子,本文将云参数输入辐射传输模式来考虑云的影响。根据国际卫星云气候计划(ISCCP)D2数据计算所得到的不同云态、云顶压力和光学厚度的15类云的云量和云水含量等资料参见文献(Zhang et al.,2011,张华等,2011)。其中低云的高度为1~2 km,中云 的高度为4~5 km,高云的高度为10~12 km。低云Cu、Sc、St和中云Ac、As、Ns等6种云的云粒子相态有水云和冰云两种,冰云的平均有效半径为30 μm,水云为10 μm。计算时,地表发射率设为1.0。
通过在热带、中纬度和亚极三种大气中加入云参数,可以得到有云大气下的平流层调整的辐射效率,所采用的计算方法如下:
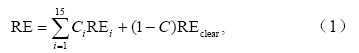
其中,Ci为每类云的云量,C=∑Ci是总云量,REclear和REi分别表示晴空和有云(云类型为i,i=1~15)大气下平流层调整的辐射效率。然后,通过公式(2)可计算全球平均的有云大气下平流层调整的辐射效率(Highwood and Shine,2000):
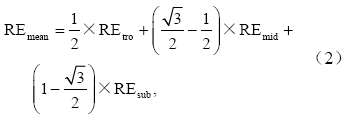
其中,REmean是全球平均平流层调整的辐射效率,REtro、REmid和REsub分别表示热带、中纬度和亚极大气平流层调整的辐射效率。
3.2 模式检验
为了检验所用模式,本文给出了两种假设情景下计算的辐射强迫结果,与Collins et al.(2006)给出的大气海洋环流模式(AOGCMs)的结果进行了比较。这两种情景包括:(1)CO2浓度由1860年287 ppm的基础上加倍至574 ppm;(2)CO2浓度加倍后(574 ppm),水汽含量增加到1860年的1.2倍。其中,CO2浓度增加时,O2相应减少。这两种情景下辐射强迫的计算结果包括(1)晴空模式顶部(TOM)的长波净辐射;(2)晴空200 hPa处的长波净辐射;(3)晴空地表(Surface)长波净辐射。
比较时,选用统一的模式大气——中纬度夏季大气(MLS),以确保所有的计算都在相同的温度廓线下进行,模式大气分为40层,大气层顶为80 km,压强为0.01 hPa,并假设温室气体混合均匀。在本文的辐射传输模式中,参数设置如下:模式中层底云浓度为零,气溶胶含量为零。忽略云和气溶胶的影响以及平流层调整的作用。
表 1给出了上述两种情景下本文的结果与Collins et al.(2006)中不同模式的计算结果。本文计算的CO2浓度加倍引起的地表、200 hPa和模式 顶部的长波辐射强迫分别为1.7 W m-2、5.6 W m-2和3.03 W m-2,CO2浓度加倍后水汽含量增加20%引起的长波辐射强迫分别为11.14 W m-2、4.13 W m-2和3.26 W m-2,如图 2中的三角图标所示。由图 2可见,本文的结果基本都位于不同大气海洋环流模式(AOGCMs)的结果和逐线积分模式(LBL)结果范围之间。对第一种情景,本文结果更接近于LBL结果;对第二种情景,本文的结果位于不同大气海洋环流模式(AOGCMs)的范围内,与LBL的结果稍有差异,其中,对CO2加倍引起的地表长波辐射强迫,本文结果更接近LBL结果。以上比较说明采用高光谱辐射传输模式进行本文的计算是合理的。
| 表 1 不同情景、不同模式下的长波辐射强迫(单位:W m-2) Table 1 Comparison among CO2 longwave radiative forcings under different conditions(unit: W m-2) |
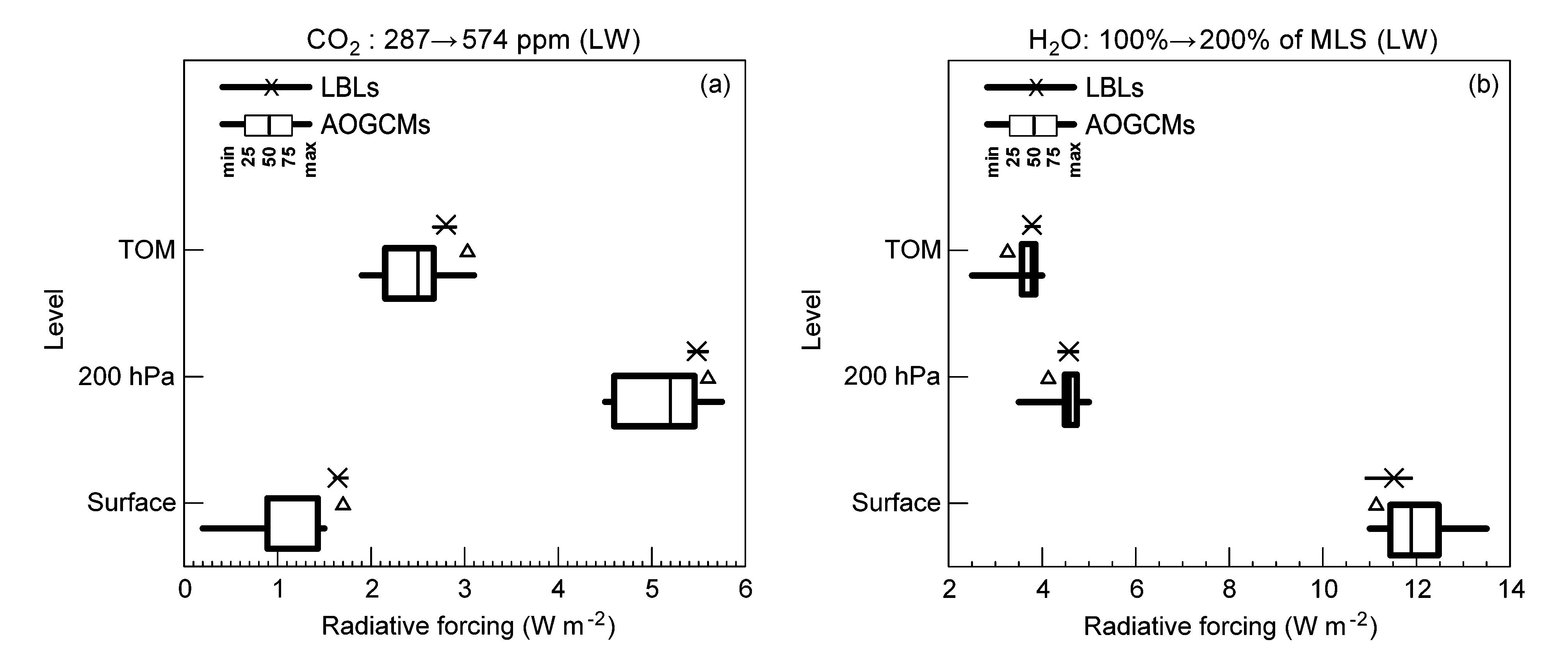 | 图 2(a)CO2 浓度从287 ppm 增加到574 ppm 的长波辐射强迫;(b)CO2 浓度加倍后,水汽含量增加20%的长波辐射强迫。三角图标表示本文计算 结果Fig. 2 (a) Longwave radiative forcing induced by increased CO2 concentration from 287 ppm to 574 ppm; (b) longwave radiative forcing induced by moisture content increased by 20% with doubled CO2 concentration. Triangles indicate the results calculated in this paper. Base map is from Collins et al. (2006) |
表 2列出了CH4和N2O晴空大气下的瞬时辐射效率和平流层调整的辐射效率,以及有云大气下的平流层调整的辐射效率。其中,晴空大气下的结果是六种模式大气的算术平均值,有云大气的结果是上面三种大气的区域加权平均值。通过对比表 2中晴空大气下瞬时辐射效率和平流层调整后的辐射效率,可以看到,经过平流层调整,CH4和N2O的辐射效率分别减少了1.3%和2.3%。平流层温度调整对辐射强迫的作用是增大或是减小,取决于平流层温度调整后,温度廓线对对流层顶净辐射通量的影响(Jain et al.,2000)。如图 3,分别给出在六种模式大气下,计算的CH4和N2O气体浓度变化为1 ppb时在长波区间引起的辐射加热率。加热率随不同模式大气而变化,但是不同模式大气的加热率量级都比较接近,并且有相似的垂直分布,可以看出,CH4、N2O的加热率在对流层顶以上的平流层都为负值,在这些大气层上起冷却作用。当平流层经过调整达到新的平衡后,平流层下部会减少向对流层的向下辐射通量,引起对流层顶的辐射强迫减少。
| 表 2 CH4和N2O的辐射效率(单位:W m-2 ppb-1) Table 2 Radiative efficiencies of CH4 and N2O(unit: W m-2 ppb-1) |
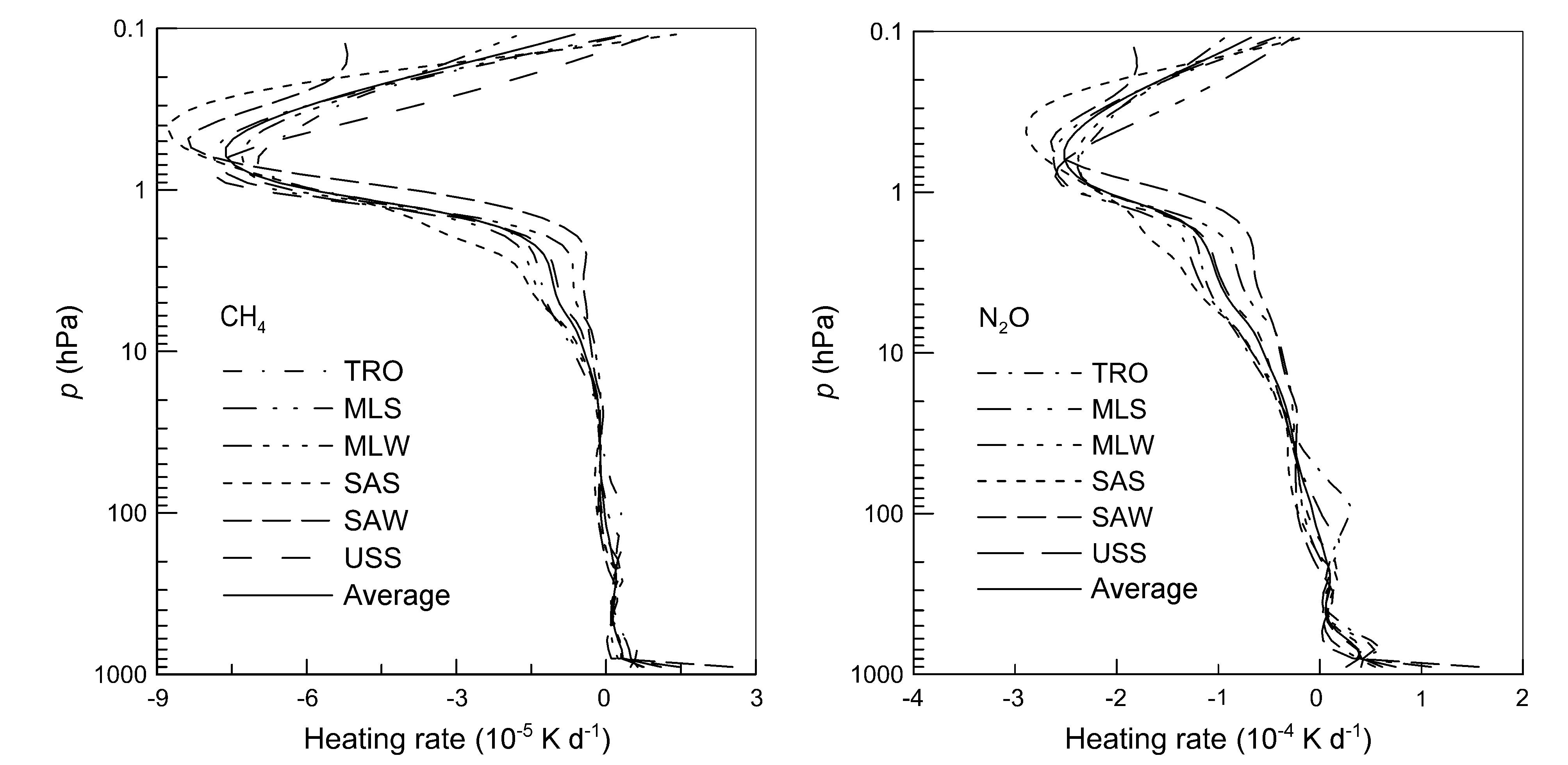 | 图 3 6 种模式大气下1 ppb CH4(a)、N2O(b)扰动的加热率Fig. 3 Heating rate of 1 ppb perturbation of (a) CH4 and (b) N2O under six kinds of model atmosphere |
| 表 3 CH4 和N2O 的20 年、100 年、500 年GWP、GTPP、GTPS 和GWP(IPCC,2007) Table 3 GWP, GTPP, GTPS, and GWP (IPCC, 2007) of CH4 / N2O with different TH (20 a, 50 a, and 100 a) |
本文采用CH4、N2O等温室气体的全球平均 浓度来计算全球平均的辐射强迫(效率),但实际 上,它们的浓度都是随高度有变化的。许多研究表明,随高度不变的廓线和变化的廓线引起的辐射强迫存在差别。Sihra et al.(2001)基于Jain et al.(2000)的工作提出了一个与大气寿命相关的调整系数来调整平流层浓度减小对辐射强迫的影响,指出对大气寿命超过0.25年的气体,该系数为1-0.241×-0.358,其中,代表大气寿命,单位为a,并且指出大气寿命调整后的辐射强迫也会有误差,但是要比完全不调整好得多(Sihra et al.,2001)。本文采用该系数计算得出,CH4和N2O经过大气寿命调整后的辐射效率分别为3.732×10-4和2.987×10-3 W m-2 ppb-1,比不经过大气寿命调整的辐射效率分别减少了9.8%和4.4%,可见大气寿命越长,调整前后的差别越小。
3.4 辐射强迫的简单计算公式
温室气体的辐射强迫,可以利用各种辐射传输模式来计算,包括逐线积分模式、带模式等,也有各种适用的气候模式。然而应用模式计算辐射强迫的运算量相对较大,会耗费大量的计算时间。而根据模式的计算结果可以得出,改变温室气体的浓度,产生的辐射强迫也相应地发生变化,且两者之间的对应关系有一定规律。因此,可以将这种对应关系表示成比较简单的经验公式,以便快速而又精确合理地计算辐射强迫。
研究表明,可定性地认为:当某种大气温室气体,或由于其吸收带的强度较弱,或由于其在大气中的浓度偏低,或是两者的综合作用,使其在大气中的吸收处于线性吸收区(即吸收率与吸收物质量成正比)时,则其辐射强迫基本上与其浓度变化成线性关系;当吸收处于平方根区(吸收率正比与吸收物质量的平方根)时,则其辐射强迫基本上与 其浓度变化成平方根关系;当吸收更强时,其辐 射强迫与浓度变化将变成对数关系(石广玉,1991,2007)。
计算CH4浓度在一定范围内变化造成的平流层调整的辐射强迫时,必须考虑其与CO2、H2O、O3和N2O之间的重叠吸收。根据石广玉等(1991,2007)、于秀兰等(2001)的研究结果,只需考虑N2O浓度的变化对吸收重叠的影响,其它可以忽略不计。本文引用了文献(石广玉,1991,2007;于秀兰等,2001)中的简化公式形式重新对平流层调整后的辐射强迫进行了拟合,在计算CH4浓度变化造成的辐射强迫时,只考虑了N2O浓度变化对重叠效应的影响;同时,利用平方根项和线性项叠加,可以得到比仅用平方根项更高的拟合精度。经过计算,得出的简单公式:

其中,M、N分别为CH4、N2O的浓度,CH4参考浓度M0=1797 ppb。4个拟合系数分别为α=0.03195,β=1.439×10-4,γ=-1.133×10-3,δ=1.221×10-7。
同理,计算N2O浓度变化造成的辐射强迫时,只考虑CH4对吸收重叠的影响,得到公式:
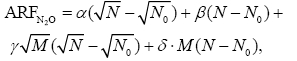
其中,M、N意义同上,N2O参考浓度N0 =321.8 ppb。4个拟合系数分别为α=0.08801,β=0.0011,γ= -3.7167×10-4,δ= 2.0116×10-9。
石广玉等(1991,2007)、于秀兰等(2001)的研究时间较早,所用的气体谱线和浓度资料都已陈旧。而本文用于公式拟合的样本数据则是由新的气体浓度和998带高光谱分辨率的辐射传输模式 重新计算出的平流层调整后的辐射强迫ARF,因此,本文拟合的公式与石广玉等(1991,2007)、于秀兰等(2001)的结果相比,不仅目标气体的背景浓度不同,计算出的气体的辐射强迫数值也更新。
使用拟合公式计算辐射强迫的优点是,当温室气体的浓度改变时,只需要一次数学公式的计算,比使用模式计算大大减少了计算量。
4 CH4和N2O的全球增温潜能和全球温变潜能
本文根据文献(Zhang et al.,2011;张华等,2011)建立的GWP和GTP模型,计算了CH4和N2O未来20、100和500年的GWP和GTP。
GWP的定义是瞬时脉冲排放1 kg化合物x,在一定的时间范围内引起的辐射强迫的积分相对 于脉冲排放等量参考气体(本文采用CO2)在同一时间范围内的辐射强迫的积分。公式如下(IPCC,2007):
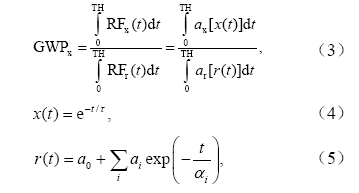
全球温变潜能(GTP)的定义为:在脉冲排放1 kg化合物x或者以1 kg·a-1递增的持续排放化合物x,在给定的一段时间TH内造成的全球平均地表温度的变化与参考气体r(本文采用CO2)所造成的相应变化之比。脉冲排放和持续排放的GTP分别表示为GTPP和GTPS(Shine et al.,2005),公式如下:
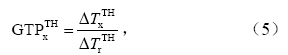
其中,TH表示时间范围(这里为20、100和500年);ΔTx和ΔTr分别表示化合物x和CO2引起的全球平均地表温度变化,它们可以通过求解全球平均地表温度变化ΔT与辐射强迫ΔF之间的公式(Shine et al.,2005)得到,
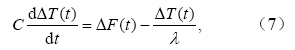
其中,t表示时间,C是系统的热容量,λ是气候灵敏度参数。
脉冲排放和持续排放的绝对全球温变潜能分别记为AGTPP和AGTPS,表示在初始时刻排放的气体在时间t时刻引起的地表温度的变化,单位为K kg-1和K(kg a-1)-1。故脉冲排放和持续排放的GTP也可以分别表示为(Zhang et al.,2011;张华等,2011)
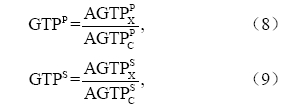
即GTP可表示为化合物x与参考气体CO2的绝对温变潜能之比。计算GWP和GTP所需要的参数为气体x和CO2的辐射效率和时间响应函数。这里采用Zhang et al.(2011)计算的有云大气条件下平 流层调整的CO2辐射效率、以及本文计算的CH4和N2O的有云大气条件下平流层调整的辐射效率,CH4、N2O和CO2的时间响应函数取自IPCC(2007),气候灵敏度参数、热容量等参数取值与Shine et al.(2005)相同。表 3列出了CH4和N2O的20、100和500年的GWP,脉冲排放的GTPP和持续排放的GTPS,同时还给出IPCC(2007)的GWP值作为比较,表 4则是由大气寿命调整后的辐射效率计算得出的相应结果。计算时,CO2的大气寿命取120年,则经过大气寿命调整的CO2辐射效率为1.567×10-5 W m-2 ppb-1(Zhang et al.,2013)。通过比较表 3和表 4,可以看出不论CH4或N2O,其大气寿命调整前后的各项指数变化不大(调整后比调整前值略有减少或不变)。此后,各项指数均取大气寿命调整后的值。
| 表 4 进行大气寿命调整后,CH4 和N2O 的20 年、100 年、500 年GWP、GTPP、GTPS 和GWP(IPCC,2007) Table 4 GWP, GTPP, GTPS, and GWP (IPCC,2007) of CH4 / N2O with different TH (20 a, 50 a, and 100 a) after the atmospheric lifetime adjustment |
由表 3~4中GWP值可以看出,对于脉冲排放等量的气体,CH4和N2O对气候变化的贡献是CO2的几十至上百倍。对100年的时间范围,本文计算的CH4和N2O结果分别比IPCC(2007)的结果小32%和11%,用经过大气寿命调整的辐射效率计算出的结果则分别小28%和3%。通过对公式(3)的分析得出,GWP计算主要与四个参数直接相关,即气体的辐射效率和时间响应函数以及参考气体CO2的辐射效率和时间响应函数,它们共同作用造成GWP值的计算差别。经分析可以得出,本文GWP的差别主要是由CH4、N2O辐射效率的不同造成的,其中本文采用了高精度的辐射传输模式是其中差别的主要原因。
对比表 3~4中GTPP值和GWP值,除了大气寿命较长的N2O其20年的GTPP值略大于GWP值,其他GTPP值都小于相应的GWP值,500年GTPP值更是远远小于GWP值;而且对于大气寿命较小的CH4,两者的差别大于N2O。Zhang et al.(2011),张华等(2011)的研究也表明,大气寿命越小的气体,GTPP值和GWP值相差越大。这是因为对大气寿命较小的气体,GWP值大大高估了气体脉冲排放对气候变化的影响(Shine et al.,2005)。
GTPS考虑的是气体在持续排放情况下对地表温度的变化产生的相对影响,而在实际中,CH4和N2O的排放量正是持续增加到大气中的。通过对比表 3~4中GTPS值和GWP值可以发现,两者的差别要比同一气体相同时间范围的GTPP值与GWP值的差别小,并且随着时间范围的增大,GTPS值与GWP值差别减小。Zhang et al.(2011)和张华等(2011)分别对HFCs、PFCs、SF6等温室气体的研究也显示了这一特性,并给出了解释:虽然GTPS和GWP的概念相差很大,但在时间跨度较大的情况下GTPS与GWP有相似的数学表达式,因而得到的结果也接近(Shine et al.,2005)。
本文还计算了CH4、N2O在未来500年内的绝对全球温变潜能AGTPP和AGTPS,表示这些气体脉冲排放或者持续排放在未来500年内引起的地表温度变化,见图 4。由图 4a可见,N2O脉冲排放的气体引起的地表温度在排放初期迅速增加,并且在排放后40年左右达到一个最大值,然后地表温度开始缓慢恢复,在未来400年后完全得到恢复;CH4则是自开始的几十年内由最大值迅速减小,其后50年左右就得到完全恢复。可以发现,地表温度恢复的快慢与气体的大气寿命长短相关,大气寿命较短的CH4恢复得较快,大气寿命较长的N2O则恢复得较慢,从量级上看,N2O比CH4对地表温度变化的影响也要大。图 4b显示,N2O持续排放引起的地表温度的变化从排放时刻起一直增加,到本文计算的节点500年达到最大并开始变缓;而CH4持续排放在整个计算时间范围内对地表温度变化的影响都比N2O小得多,其变化缓慢。通过图 4还可看 出,CH4和N2O气体持续排放引起的地表温度变化要比其脉冲排放引起的相应值大两个数量级,对地表温度变化的影响要大得多。从本文的计算得出:如果对N2O的排放不加以控制,它会对未来地表温度变化的产生持续影响并且很难得到恢复,而CH4对未来气候变化的影响比N2O小得多,且比较容易得到恢复。
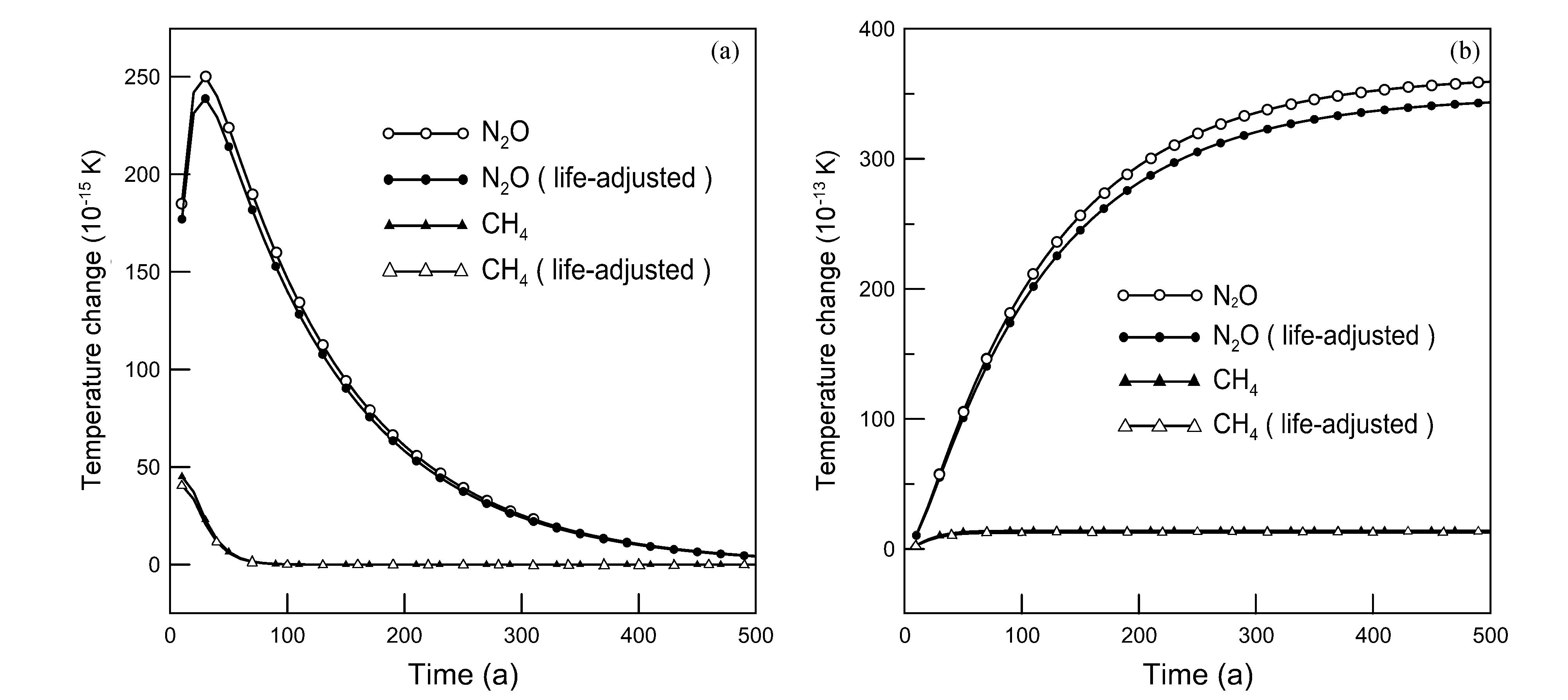 | 图 4 CH4 和N2O 脉冲排放(a)和持续排放(b)引起的地表温度变化Fig. 4 Surface temperature changes induced by (a) pulse emission and (b) sustained emission of CH4/N2O |
本文计算了晴空大气和有云大气下主要温室气体CH4和N2O的瞬时辐射效率和平流层调整的辐射效率,得出:(1)经过平流层温度调整,CH4和N2O的辐射效率均相对减小,这取决于平流层温度调整后,平流层温度变冷,导致其向对流层辐射通量减少所致。(2)本文计算的CH4和N2O经 过大气寿命调整的辐射效率均与IPCC(2007)的结果高度一致,差别仅为0.86%和1.4%。
以本文计算的CH4和N2O新的辐射效率为基础,进一步研究了CH4、N2O在未来20、100、500年时间尺度上的GWP和GTP,并分别计算了CH4和N2O脉冲排放、持续排放在未来500年内引起的地表温度变化。结果表明:对于脉冲排放等量的气体,CH4和N2O的GWP值与对应的GTPP值相比显著偏高,说明GWP测量方法大大高估了CH4和N2O对气候变化的影响。
通过本文的计算和比较分析得出,持续排放CH4和N2O引起的地表温度变化要比其脉冲排放引起的相应值大两个数量级,对未来地表温度变化的影响要大得多。CH4对未来地表温度变化的影响比N2O小得多,而且比较容易得到恢复。如果对N2O的排放不加以控制,它会对未来地表温度变化的产生持续的影响并且很难得到恢复。因此控制N2O的排放迫在眉睫。另外,本文晴空的计算结果是对六种模式大气算术平均得出的,而有云情况是对三个纬度带进行面积加权平均得到的,其中造成的不确定性也许会大于辐射模式计算精度本身造成的不确定性。
| [1] | Collins W D, Ramaswamy V, Schwarzkopf M D, et al. 2006. Radiative forcing by well-mixed greenhouse gases: Estimates from climate models in the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4) [J]. J. Geophys. Res., 111: D14317, doi:10. 1029/2005JD006713. |
| [2] | Fuglestvedt J S, Berntsen T K, Godal O, et al. 2003. Metrics of climate change: Assessing radiative forcing and emission indices [J]. Climatic Change, 58: 267-331. |
| [3] | Garand L, Turner D S, Larocque M, et al. 2001. Radiance and Jacobian intercomparison of radiative transfer models applied to HIRS and AMSU channels [J]. J. Geophys. Res., 106 (D20): 24017-24031. |
| [4] | Highwood E J, Shine K P. 2000. Radiative forcing and global warming potentials of 11 halogenated compounds [J]. J. Quant. Spectrosc. Radiat. Transf., 66: 169-183. |
| [5] | 黄兴友. 2001. 温室气体全球增温潜能的研究 [D]. 中国科学院大气物理研究所博士学位论文. 107pp. Huang Xingyou. 2001. Study on global warming potential of greenhouse gas [D]. Ph. D. dissertation (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Sciences, 107pp. |
| [6] | IPCC. 1996. Climate Change 1995: The Science of Climate Change [M] // Houghton J T, Fiho L G M, Callander B A, et al. Contribution of Working Group II to the Second Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, U K and New York: Cambridge University Press. |
| [7] | IPCC. 2007. Climate Change 2007: The Physical Science Basis [M] // Solomon S, Qin D, Manning M, et al. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge and New York: Cambridge University Press. |
| [8] | Jain A K, Briegleb B P, Minschwaner K, et al. 2000. Radiative forcings and global warming potentials of 39 greenhouse gases [J]. J. Geophys. Res., 105 (D16): 20773-20790. |
| [9] | Lu P, Zhang H, Jing X W. 2012. The effects of different HITRAN versions on calculated longwave radiation and uncertainty evaluation [J]. Acta Meteorologica Sinica, 26 (3): 389-398 doi:10.1007/s13351-012- 0310-1. |
| [10] | Nakajima T, Tsukamoto M, Tsushima Y, et al. 2000. Modeling of the radiative process in an atmospheric general circulation model [J]. Appl. Opt., 39: 4869-4878. |
| [11] | Rothman L S, Jacquemart D, Barbe A, et al. 2005. The HITRAN 2004 molecular spectroscopic database [J]. J. Quant. Spectrosc. Radiat. Transf., 96: 139-204. |
| [12] | Shi G Y. 1981. An accurate calculation and representation of the infrared transmission function of the atmospheric constituents [D]. Ph. D. dissertation, Tohoku University of Japan, 191pp. |
| [13] | 石广玉. 1991. 大气微量气体的辐射强迫与温室气候效应 [J]. 中国科学(B辑), 35 (7): 776-784. Shi Guangyu. 1991. Radiation forcing and greenhouse effect of atmospheric trace gases [J]. Science China Chemical Sciences (in Chinese), 35 (7): 776-784. |
| [14] | 石广玉. 2007. 大气辐射学 [M]. 北京: 科学出版社, 402pp. Shi Guangyu. 2007. Atmospheric Radiation (in Chinese) [M]. Beijing: Science Press, 402pp. |
| [15] | Shine K P, Fulestvedt J S, Hailemariam K, et al. 2005. Alternatives to the global warming potential for comparing climate impacts of emissions of greenhouse gases [J]. Climatic Chang, 68 (3): 281-302. |
| [16] | Sihra K, Hurley M D, Shine K P, et al. 2001. Updated radiative forcing estimates of 65 halocarbons and nonmethane hydrocarbons [J]. J. Geophys. Res., 106 (D17): 20493-20505. |
| [17] | World Meteorological Organization (WMO). 2009. Greenhouse Gas Bulletin: The state of greenhouse gases in the atmosphere using global observations through 2008 [R]. Geneva: World Meteorological Organization. |
| [18] | 于秀兰, 石广玉. 2001. 平流层温度调整后的辐射强迫的简化计算[J]. 高原气象, 20 (3): 271-274. Yu Xiulan, Shi Guangyu. 2001. Simplified calculation of radiative forcing with adjusted stratosphere temperature [J]. Plateau Meteorology (in Chinese), 20 (3): 271-274. |
| [19] | Zhang H, Nakajima T, Shi G Y, et al. 2003. An optimal approach to overlapping bands with correlated k distribution method and its application to radiative calculations [J]. J. Geophys. Res., 108 (D20): 4641, doi:10.1029/2002JD003358. |
| [20] | Zhang H, Shi G Y, Nakajima T, et al. 2006a. The effects of the choice of the k-interval number on radiative calculations [J]. J. Quant. Spectrosc. Radiat. Transf., 98 (1): 31-43. |
| [21] | Zhang H, Suzuki T, Nakajima T, et al. 2006b. Effects of band division on radiative calculations [J]. Opt Eng, 45 (1): 16002-16010. |
| [22] | Zhang H, Wu J X, Lu P. 2011. A study of the radiative forcing and global warming potentials of hydrofluorocarbons [J]. J. Quant. Spectrosc. Radiat. Transf., 112 (2): 220-229. |
| [23] | Zhang H, Zhang R Y, Shi G Y. 2013. Radiative forcing due to CO2 and its effect on global surface temperature change [J]. Advances in Atmospheric Sciences,30 (4). |
| [24] | 张华, 吴金秀, 沈钟平. 2011. PFCs和SF6的辐射强迫和全球增温潜能 [J]. 中国科学, 41 (2): 215-233. Zhang Hua, Wu Jingxiu, Shen Zhongping. 2011. Radiative forcing and global warming potential of perfluorocarbons and sulfur hexafluoride [J]. Science China Earth Sciences, 54 (5): 764-772, doi:10.1007/s11430-010-415-0. |
 2013, Vol.
2013, Vol.