1 引言

陆面模式是大气模式中不可或缺的一部分。提高陆面模式的模拟能力，解决其与大气模式耦合中存在的问题，是提高大气模式模拟和预报能力的关键。陆面模式模拟真实世界的能力主要取决于三点(Duan et al.,2006)：第一，模型本身结构(如：模型方程或参数化方案)的真实性；第二，外部强迫场以及边界和初始条件的可靠性；第三，模型参数估计的合理性。目前，估计模型参数的方法主要有两种(Duan et al.,2003)：先验方法和参数校准方法。其中，先验方法是依赖理论或经验上参数与陆面模式的观测特征(比如土壤和植被的属性)的关系来估计参数。而参数校准方法是通过调整参数取值来使模式的模拟结果与观测数据很好地吻合。在观测数据充足、可靠的时候，参数校准方法可以得到更合理的参数估计结果。

陆面模式的合理参数估计是保证陆面模式模拟结果可靠性的前提。然而，由于陆面模式同时考虑水量和能量交换平衡过程，而且下垫面的组成复杂，因此，陆面模式中包含了大量的参数，而参数之间存在复杂的相互作用加大了模式参数合理估计的难度。现有优化算法［如遗传算法(Goldberg，1989)、SCE-UA算法(Duan et al.,1993)］在高维参数空间的搜索效率有限，而陆面模式又需要较高的运算成本，导致参数优化工作需要极长的模拟时间。因此，传统参数率定方法不再适用。鉴于传统优化算法的局限性，陆面模式的参数估计可以借助统计和试验设计的手段，本研究提出对陆面模式参数降维的方法。具体的实现手段是通过敏感性分析，筛选出对于目标变量模拟最重要的参数，并把陆面模式参数的维数降至10个左右(Tong and Graziani，2008)。

敏感性分析是研究模型输出变化对系统参数变化的敏感程度的方法，它可以分为定性敏感性分析方法和定量敏感性分析方法。定性敏感性分析 方法用于筛选影响模型输出的敏感参数，而定量敏感性分析方法用于研究模型中每个参数的敏感程度。近几十年来，科研工作者在模型参数筛选和敏感性分析的问题上做了大量的研究，开发出许多方法。Campolongo and Saltelli(1997)应用敏感性分析方法对一个从藻类生物中生产硫化物的模型进行分析，先用定性方法筛选出重要参数，然后用计算量较大的基于方差的敏感性分析方法进行定量分析。De Pauw et al.(2008)在树的水流动和存储模型中，利用定性和定量的敏感性分析方法，将 茎液流量和阀杆直径的变化分解成不同的组分。Yamwong and Achalakul(2011)使用一个基于因子设计的改良的参数筛选析因算法，它能够分析更多的参数，可以在合理的计算时间内筛选出重要的参数并考查参数间的交互作用。目前敏感性分析方法大多是应用于参数少、运算成本低的简单模型，目的是获得更多参数信息，而不是为了更有效地估计参数。一些复杂模型中应用敏感性分析方法也只是为了研究某几个参数对输出结果的影响程度。而本研究针对复杂模式中所有参数，旨在利用敏感性分析方法实现复杂模式的参数筛选，以便进一步做参数优化。

本研究选取大复杂动力系统模式CoLM(Common L and Model)为研究对象，利用敏感性分析方法在CoLM的40个可调参数中选出对土壤温度和土壤湿度影响较大的参数。由于CoLM模式运算成本较高，所以本研究使用基于少量样本的Morris定性方法筛选出重要参数。为了验证Morris方法的有效性，研究使用Sobol′ 方法通过较多的样本定量分析参数的敏感性，最终应用Sobol′ 方法对筛选出的敏感参数做定量敏感性分析，确定主效应、交互效应和总效应。通过本研究，可以为大复杂动力系统模式的参数估计提供科学借鉴，最终实现提高模式模拟与预测能力的目的。

2 CoLM模式及可调参数 2.1 CoLM简介

CoLM(Dai et al.,2003)是一个国际上比较流行的陆面模式。该模式建立在LSM(L and Surface Model)(Bonan，1996)、BATS(Biosphere-atmosphere transfer scheme)(Dickinson et al.,1993)、IAP94(In- stitute of Atmospheric Physics l and -surface model)(Dai and Zeng，1997)三个模式的基础上，并且不断扩充考虑不同的物理过程如冰川、湖泊、湿地、动态植被，目前它已经被多个气候模式广泛采纳。

CoLM考虑了陆面的生态、水文等过程，对土壤—植被—积雪—大气之间能量与水量传输进行了较好地描述。模式有一个基于 LSM可以实现光合作用的植被层，和一个底部达到3.43 m深的10层不均匀垂直土壤层；同时，模式考虑了向上的5层雪层。模式中的土壤水热性质参数化方案取自Farouki(1986)、Clapp and Hornberger(1978)及Cosby et al.(1984)的参数化方案。雪参数化方案参考了Jordan(1991)及Dai and Zeng(1997)的参数化方案。

2.2 可调参数的确定

本研究从CoLM中选择了40个不随时间变化的可调参数。表 1解释了可调参数的物理意义和取值范围，其中参数的取值范围是与CoLM的开发者戴永久教授商榷后确定的。

表 1(Table 1)

表 1 参数及其取值范围 Table 1 Parameters and their ranges 编号 参数 物理意义 取值范围 P1 dewmx 最大叶面积水量 [0.05，0.15] P2 hksati 饱和导水率 [0.001，1] P3 porsl 土壤孔隙度 [0.25，0.75] P4 phi0 最小土壤毛细势 [50, 500] P5 wtfact 浅地下水位区域面积比例 [0.15，0.45] P6 bsw Clapp and Hornbereger “b”参数 [2.5，7.5] P7 wimp 孔隙度的下确界 [0.01，0.1] P8 zlnd 土壤表面粗糙度 [0.005，0.015] P9 pondmx 土壤表面最大积水深度 [5, 15] P10 csoilc 冠层下土壤表面拖曳系数 [0.002，0.006] P11 zsno 积雪表面粗糙度 [0.0012，0.0036] P12 capr 表层土壤温度可调参数 [0.17，0.51] P13 cnfac Crank Nicholson因子 [0.25，0.5] P14 slti 植被低温抑制斜率 [0.1，0.3] P15 hlti 植被低温抑制二分点 [278, 288] P16 shti 植被高温抑制斜率 [0.15，0.45] P17 sqrtdi 植被叶片尺寸的逆平方根 [2.5，7.5] P18 effcon 植被光合作用光子转换效率 [0.035，0.35] P19 vmax25 植被光合作用最大羧化量 [10×10-6，200×10-6] P20 hhti 植被高温抑制二分点 [305, 315] P21 trda 叶面气孔导度—光合模型温度系数 [0.65，1.95] P22 trdm 叶面气孔导度—光合模型温度系数 [300, 350] P23 trop 叶面气孔导度—光合模型温度系数 [250, 300] P24 gradm 叶面气孔导度—光合模型斜率 [4, 9] P25 binter 叶面气孔导度—光合模型截距 [0.125，0.375] P26 extkn 叶片氮分配系数 [0.5，0.75] P27 chil 叶片角度分布因子 [－0.3，0.1] P28 ref(1，1) 叶片反射率(可见光，活叶) [0.07，0.105] P29 ref(1，2) 叶片反射率(可见光，死叶) [0.16，0.36] P30 ref(2，1) 叶片反射率(近红外，活叶) [0.35，0.58] P31 ref(2，2) 叶片反射率(近红外，死叶) [0.39，0.58] P32 tran(1，1) 叶片透射比(可见光，活叶) [0.04，0.08] P33 tran(1，2) 叶片透射比(可见光，死叶) [0.1，0.3] P34 tran(2，1) 叶片透射比(近红外，活叶) [0.1，0.3] P35 tran(2，2) 叶片透射比(近红外，死叶) [0.3，0.5] P36 z0m 空气动力学粗糙长度 [0.05，0.3] P37 ssi 积雪的最大束缚水含量 [0.03，0.04] P38 smpmax 植被凋萎水势上确界 [－2×105，－1×105] P39 smpmin 植被凋萎水势下确界 [－1×108，－9×107] P40 trsmx0 植被最大蒸散量 [1×10-4，100×10-4]

表 1 参数及其取值范围 Table 1 Parameters and their ranges

3 试验数据与方法 3.1 试验数据

本研究选取黑河流域的阿柔冻融观测站为研究站点(图 1，见文后彩图)。该站点位于青海省祁连县中东部地区的阿柔乡草大板村瓦王滩牧场。经、纬度为(100°28ʹE，30°08ʹN)，海拔高度为3032.8 m。试验场建在黑河上游支流八宝河南侧的河谷高地上，周围地势相对平坦开阔，自东南向西北略有倾斜下降，南北两侧约3 km外是连绵的山丘和高山。瓦王滩牧场是当地牧民的冬季牧场，夏季牧草长势良好，植被高度在20～30 cm之间。选择此站点基于两点考虑：一是中国科学院西部行动计划(二期)项目“黑河流域遥感—地面观测同步试验与综合模拟平台建设”为本研究提供了可靠的数据支持，而在黑河综合遥感联合试验气象数据集中，阿柔站点的气象数据具有观测时间长、缺失和问题数据少的特点，适合本研究；二是该试验场的地理环境符合大气边界层近地层理论中水平均匀下垫面的要求。

图 1

Fig. 1

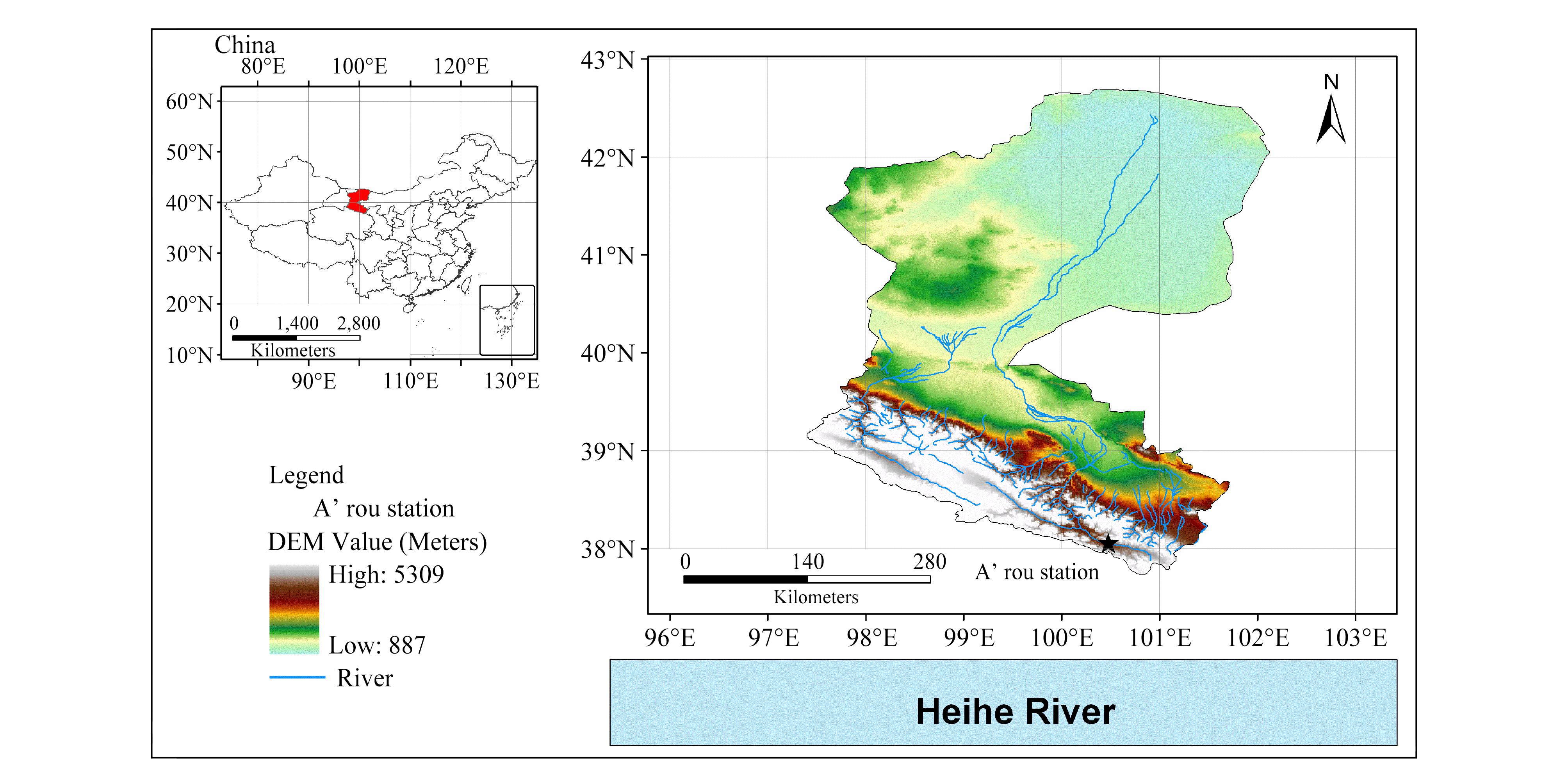图 1 阿柔观测站的地理位置Fig. 1 The location of A’rou observation station

3.1.1 驱动资料

CoLM模式所需的驱动资料有下行短波、下行长波、降雨、2 m的空气温度与比湿、气压以及10 m的风速。表 2展示了搜集的驱动资料的情况。

表 2(Table 2)

表 2 阿柔站点驱动资料 Table 2 The forcing data taken from A’rou observation station 下行 短波 下行 长波 降雨 2 m 温度 2 m相 对湿度 气压 10 m 风速 单位 W m-2 W m-2 m-2 mm °C ％ hPa m/s 时间段 2008-01-01至2009-12-31 时间步长 0.5 h 0.5 h 1 h 0.5 h 0.5 h 1 h 0.5 h 注：数据来源于国家自然科学基金委员“中国西部环境与生态科学数据中心”(http://westdc.westgis.ac.cn [06])，所有驱动资料的时间段都是2008-01-01至2009-12-31。

表 2 阿柔站点驱动资料 Table 2 The forcing data taken from A’rou observation station

3.1.2 验证资料

本研究选定土壤温度和土壤湿度为模式模拟的验证资料。土壤温度和土壤湿度是陆气相互作用中的关键物理量，在天气和气候模式中有着重要作用，通过影响地表的感热、潜热输送，进而影响当地的气候变化。在实地监测过程中，分别针对土壤剖面中10 cm、20 cm、40 cm和80 cm深度的土壤温度和湿度进行监测。而CoLM模拟结果得到的 是10层的土壤温度和湿度，这10层的深度请参见表 3。所以，研究中使用线性插值方法计算与观测相对应的土壤温度和湿度值。以10 cm的土壤温度为例：

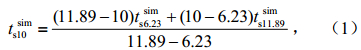
其中，t^sim_s6.23、t^sim_s10和t^sim_s11.89分别是6.23 cm、10 cm和11.89 cm土壤温度的模拟值。

表 3(Table 3)

表 3 CoLM中的10层土壤深度 Table 3 The depth of 10 layers of soil in CoLM 层数 1 2 3 4 5 6 7 8 9 10 深度(cm) 0.71 2.79 6.23 11.89 21.22 36.61 61.98 103.80 172.76 286.46

表 3 CoLM中的10层土壤深度 Table 3 The depth of 10 layers of soil in CoLM

考虑到研究的目的、数据的质量等因素，本研究模拟的时间段为2009年1月1日至2009年12月31日，时间步长定为3小时。

3.2 研究方法

本研究使用被广泛应用的全局敏感性分析方法：Morris方法和Sobol′ 方法。其中，Morris方法可以基于少量样本完成定性参数筛选，而Sobol′ 方法基于较多的样本，用来验证Morris方法的结果并进一步地对参数做定量敏感性分析。

3.2.1 Morris方法

Morris方法(Morris，1991)能在全局范围内研究模型参数的敏感性，即对系统输出的影响程度。Morris法的设计基于计算“基本作用”，其采样设计巧妙，可以以较小的计算代价得到参数全局敏感性的比较及参数相关性和非线性的定性描述。

设系统模型为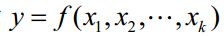，其中k为参数的维数。根据 Morris法的抽样准则，先将每个参数的变化范围映射到区间 ^{[0, 1]}，并将其离散化，使每个参数只能从集合A={0，1/p－1，2/p－1，…，1}中取值，其中p为参数的水平数。这样，每个参数在A中随机地取值获得第一个样本点X₁=(x₁，x₂，…，x_k)。要得到第二个样本点，对X¹的任意一个参数x_i作一个扰动D(D是1/p－1的整数倍)，这样得到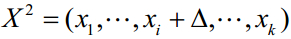。再对X²的第i个参数以外的任意参数作一个扰动 D 得到X³。以此类推，最后得到第一组k+1个样本点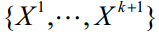。这样，由第一组样本点可以求出每个参数的基本作用，其中第j个参数的基本作用可以表示为

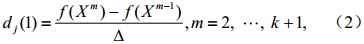
其中

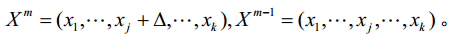
如果只考虑一组样本点，就类似于传统的局部敏感性分析方法。Morris方法之所以是全局敏感性分析方法，是因为上述的过程被重复了r次(r为预先确定的整数)来使得样本点可以代表整个样本空间。在Morris法中，假定衡量参数x_i敏感性的基本作用服从某种分布F_i，测量分布F_i的均值m _j和标准差s _j，即可确定该参数的全局敏感性。

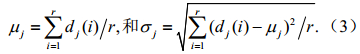
更为有效的调整的Morris方法(Campolongo et al.,2007)中，

如果x_j所对应的均值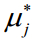越大，说明它对系统输出的影响越大。而标准差s_j表示参数之间相互作用的程度，如果标准差大，表示x_j与其它参数相互作用的程度大；反之则小。常用的Morris参数筛选方法是画出的散点图，被分离开的点对应的参数就是被筛选的参数。由这个方法可知Morris方法的局限性，也就是它只适用于敏感参数的个数远远小于全部的参数的情况。

3.2.2 Sobol′ 方法

Sobol′ 敏感性分析方法(Sobol′，1993，2001)是应用广泛的基于方差的全局敏感性分析方法，该方法的核心思想是把模型分解为递增项之和。假设模型为Y=f(X)=f(x₁,x₂,...,x_n)，x_i服从 [ 0, 1 ] 均匀分布，且f²(x)可积，模型可分解为：

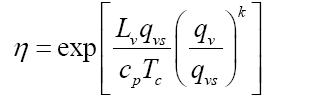
其中f₀是常数项。由方差分析的知识可以得到，

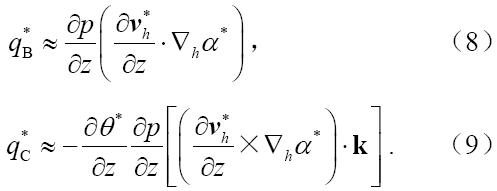
其中，V是总方差，V_i是单因子方差，V_ij是双因子方差，以此类推，V_{1，2，…，n}是所有因子的方差。对上式做归一化处理，两边同时除以V，得到

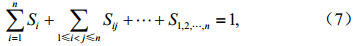
其中，S_i=V_i/V是反映主效应的敏感度，代表因子x_i的一阶主效应；S_ij = V_ij/V是反映交互作用的敏感度，代表因子x_i与x_j的二阶交互效应，以此类推。

而因子x_i的总效应敏感度S_Ti=∑S(_i)，其中S_(i)

是包含因子x_i的敏感度。总效应也可以通过下式求得，其中V_―i是除去x_i后的方差。

3.2.3 目标函数的确定

为了最终实现参数筛选，构建标准化形式的目标函数：

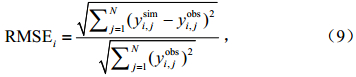
其中，N代表观测变量的数量，j是时间步长。y^sim_i,j和y^obs_i,j是模式的模拟变量和观测变量，i取值1到4，分别代表 4层的目标变量。为了研究方便，用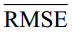表示目标的平均值，即

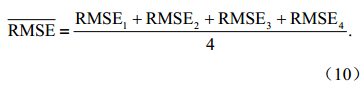
目标函数体现了模式模拟能力的好坏，本研究目标函数值越小，表示模式模拟的越准确。

3.2.4 筛选结果的验证

研究中借助Sobol′ 总效应分析方法从两个角度来验证Morris方法的参数筛选结果。一是用Sobol′总效应指标来验证参数的敏感性顺序；二是用筛选参数的累积贡献率来验证Morris筛选结果的有效性。

同时，本研究引入贡献率的概念。定义第i个参数的贡献率为：

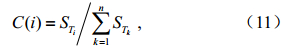
而参数集合A的累积贡献率为：

4 研究结果与分析

本研究中的主要研究工具是软件包PSUADE(Tong，2005)(Problem Solving environment for Un- certainty Analysis and Design Exploration)。PSUADE提供了大量支持大复杂动力系统模式的全局参数敏感性分析方法，其中包括本研究中涉及的Morris方法和Sobol′ 方法。

4.1 Morris定性参数筛选

Morris方法需要的样本量是n＋1(n为参数数量)的整数倍，为了探究能得到合理结果的最佳样本量，分别设置样本量为82、246和410。

Morris方法的参数筛选过程比较主观，分别画出各个样本量下的土壤温度和土壤湿度的Morris分析散点图(见图 2)，被分离开的参数就是筛选的结果，研究中用红色的圆角矩形圈出筛选出来的参数。从图中可以清楚地看到，无论是土壤温度还是土壤湿度，随着样本量的增大，Morris方法筛选出参数的数量会增加。可见，基于少量样本的Morris分析只能保证筛选出最重要的几个参数，而随着样本量的增加，会陆续筛选出其他一些比较重要的参数。本研究暂把410个样本的结果作为参数筛选结果，对于土壤温度，敏感参数有 {P2，P3，P4，P6，P19，P36}；对于土壤湿度，敏感参数有{P2，P3，P4，P6，P19}。这样就从40个参数中筛选出了对土壤温度和土壤湿度影响较大的参数。因为筛选出来的参数的数量相对于参数的总数是比较小的，所以可以认为Morris方法适用于此问题。从图中还可看出，土壤温度筛选出的6个参数还可以分成两组，P3、P6和P36显然比P2、P4和P19敏感度更 高。同样的，土壤湿度筛选出的参数中，P3和P6敏感度更高一些。

图 2

Fig. 2

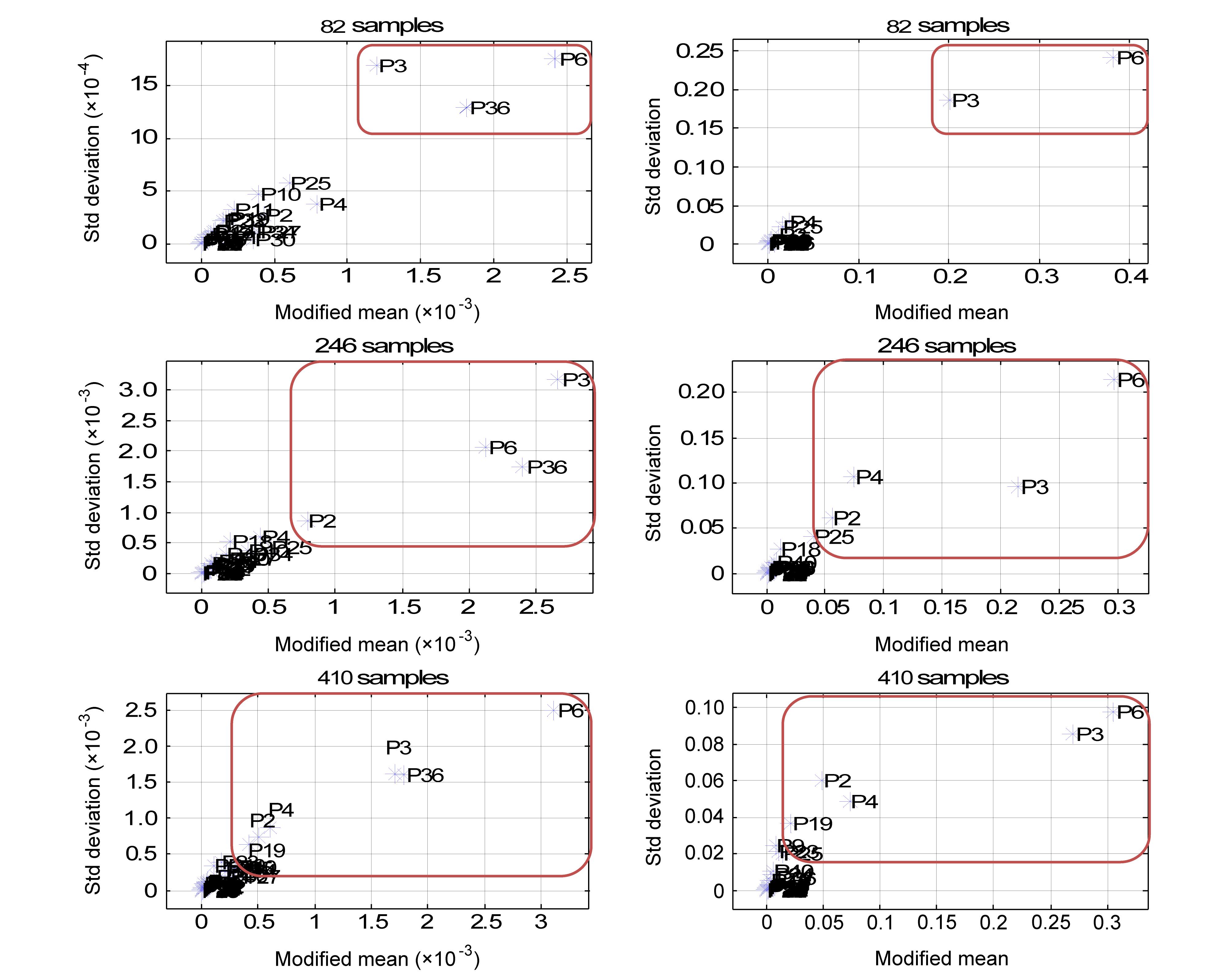图 2 不同样本量下土壤温度(左列)和土壤湿度(右列)的Morris分析散点图Fig. 2 Modified Morris diagram for soil temperature(left) and moisture(right)under conditions of different sample sizes

4.2 筛选结果的定量验证

为了验证Morris方法的筛选结果，本研究选用Sobol′ 总效应分析方法用2000个样本对40个参数做定量的敏感性分析。总效应反映参数对目标函数的总影响，一个参数总效应越大，说明它对目标的影响越大。

图 3显示了土壤温度和湿度的Sobol′ 总效应指标S_T，可以看出，P3、P6和P36对土壤温度的敏感度明显高于其他参数；在其他的参数中，P4相对来说更加敏感。同样的，P3和P6对土壤湿度的敏感度是显著的，其他参数中P2和P4的敏感度相对较高。这些结果与Morris分析的结果一致。

图 3

Fig. 3

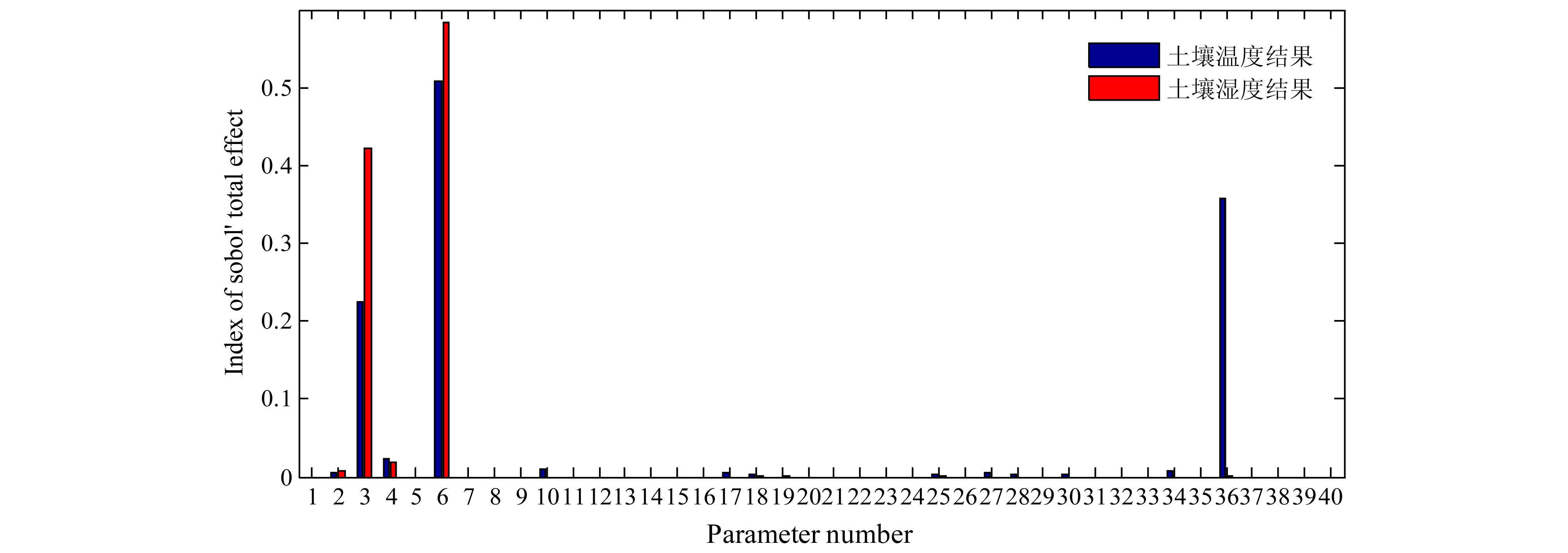图 3 土壤温度和湿度的Sobol′总效应分析结果Fig. 3 The results of Sobol′ total effect analysis for soil temperature and moisture

本研究从累积贡献率的角度来进一步验证不同样本量下Morris分析结果的有效性(见表 4)。从验证结果得知，Morris参数筛选的结果是很可靠的，仅82个样本累积贡献率也可以达到90%以上，尤其是土壤湿度，累积贡献率达到97%以上。这说明无论是对于土壤温度还是土壤湿度，重要参数的数量相对于参数总数40是很少的。而且，从累积贡献率的角度来看，Morris方法的试验设计并不需要410个样本，246个样本(即r = 4)得到的结果就是完全可以接受的。

表 4(Table 4)

表 4 不同样本量下的Morris筛选结果的累积贡献率 Table 4 The cumulative contributions of Morris screening results under conditions of different sample sizes 样本 量 土壤温度Morris 筛选 累积贡 献率 土壤湿度Morris 筛选 累积 贡献率 82 P3，P6，P36 93.75% P3，P6 97.14% 246 P2，P3，P6，P36 94.31% P2，P3，P4，P6，P25 99.89% 410 P2，P3，P4，P6，P19，P36 96.33% P2，P3，P4，P6，P19 99.73%

表 4 不同样本量下的Morris筛选结果的累积贡献率 Table 4 The cumulative contributions of Morris screening results under conditions of different sample sizes

图 4和图 5分别代表了Sobol′ 方法对影响土壤温度和土壤湿度的40个参数累积贡献率的研究结果，横坐标分别是土壤温度和土壤湿度的Sobol′ 总效应分析得到的参数敏感性顺序，纵坐标反映了引入横坐标参数后的累积贡献率。例如，图 4中横坐标为3的点对应的纵坐标为参数P6、P36和P3的累积贡献率。只要定义Sobol′ 参数筛选的累积贡献率标准就可以得出Sobol′ 定性参数筛选结果。如果样本量足够，Sobol′ 方法的参数筛选结果更可靠。但这与本研究的目的并不一致，本研究是要解决大复杂动力系统模型的参数优化问题，这些模型运算成本较高，所以Sobol′ 方法这类基于大样本量的定量敏感性分析方法并不适用。

图 4

Fig. 4

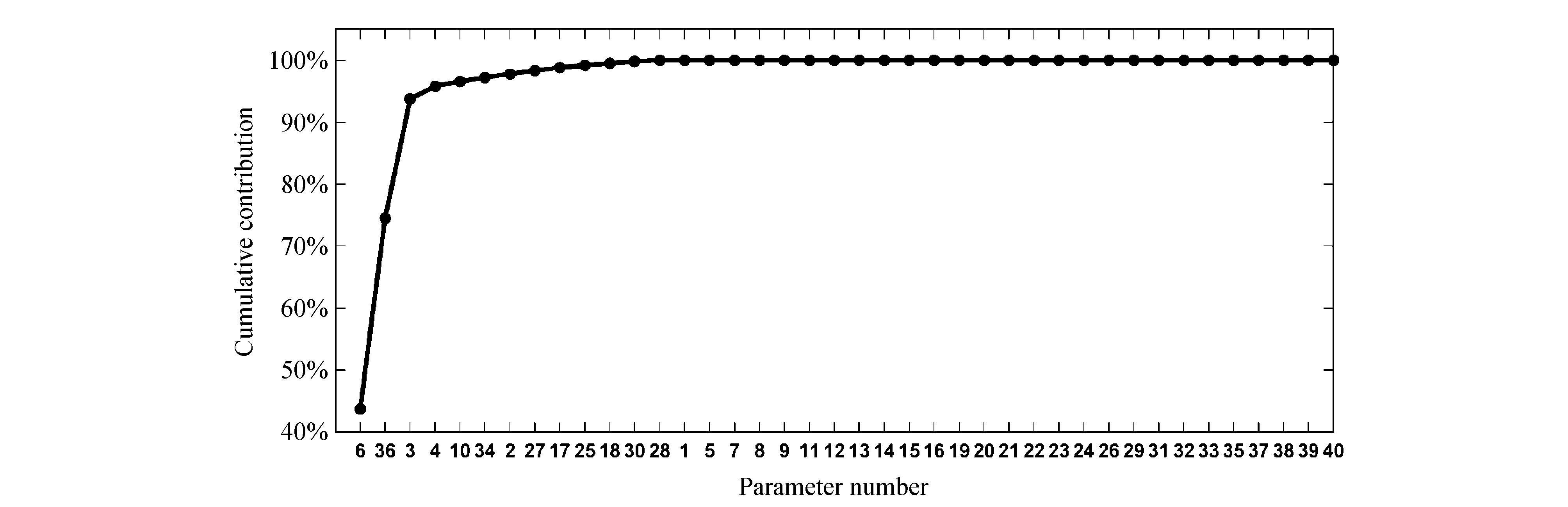图 4 土壤温度累积贡献率Fig. 4 The cumulative contribution of parameters for soil temperature

图 5

Fig. 5

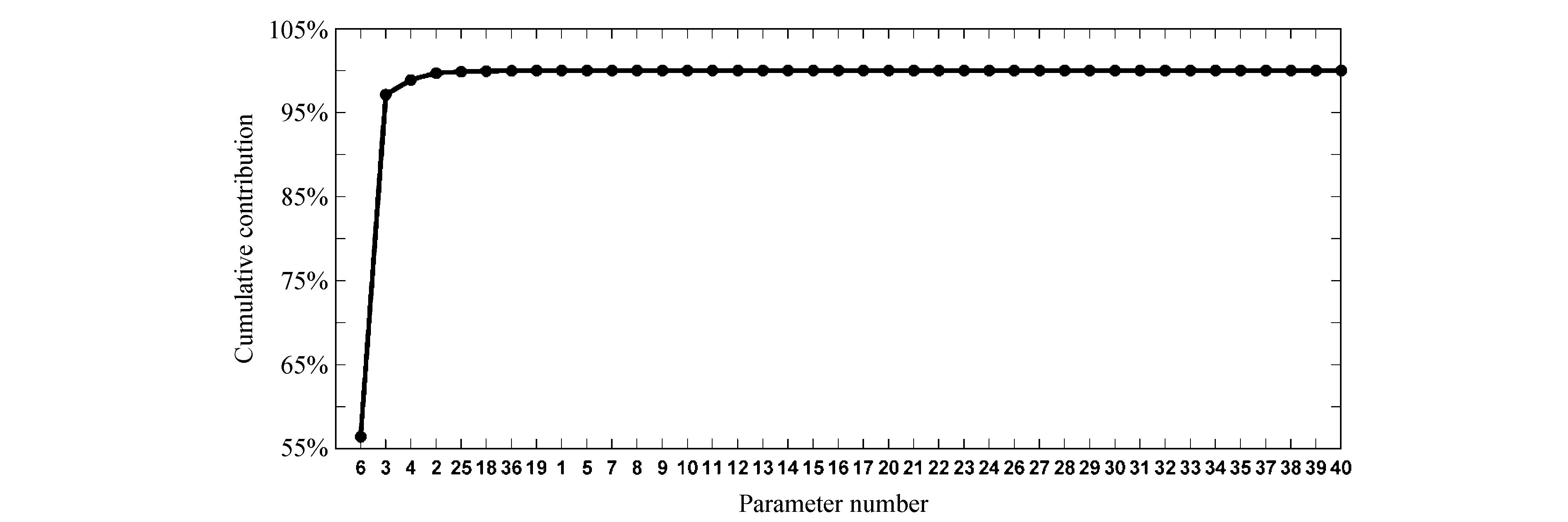图 5 土壤湿度累积贡献率Fig. 5 The cumulative contribution of parameters for soil moisture

4.3 已筛选参数的定量敏感性分析

为了进一步研究已筛选的参数，得到参数更多的敏感性信息，本研究中选取500个样本，使用Sobol′ 方法分析它们的主效应、交互效应和总效应。前面用不同的样本量对土壤温度和湿度进行Morris参数筛选，结果是有区别的，这里取各个筛选结果的并集做研究对象。对于土壤温度，研究参数集{P2，P3，P4，P6，P18，P19，P36，P40}；而对于土壤湿度，研究参数集为{P2，P3，P4，P6，P18，P19，P25，P40}。

4.3.1 主效应与总效应分析

主效应与总效应分析是反映各个参数对目标函数影响程度的重要敏感性指标，主效应反映了各参数对目标函数的一阶作用，总效应反映了各参数对目标函数的总作用。一个参数的这两个指标越大，说明它对目标函数的影响越大。图 6和图 7给出了分析结果的直方图。

图 6

Fig. 6

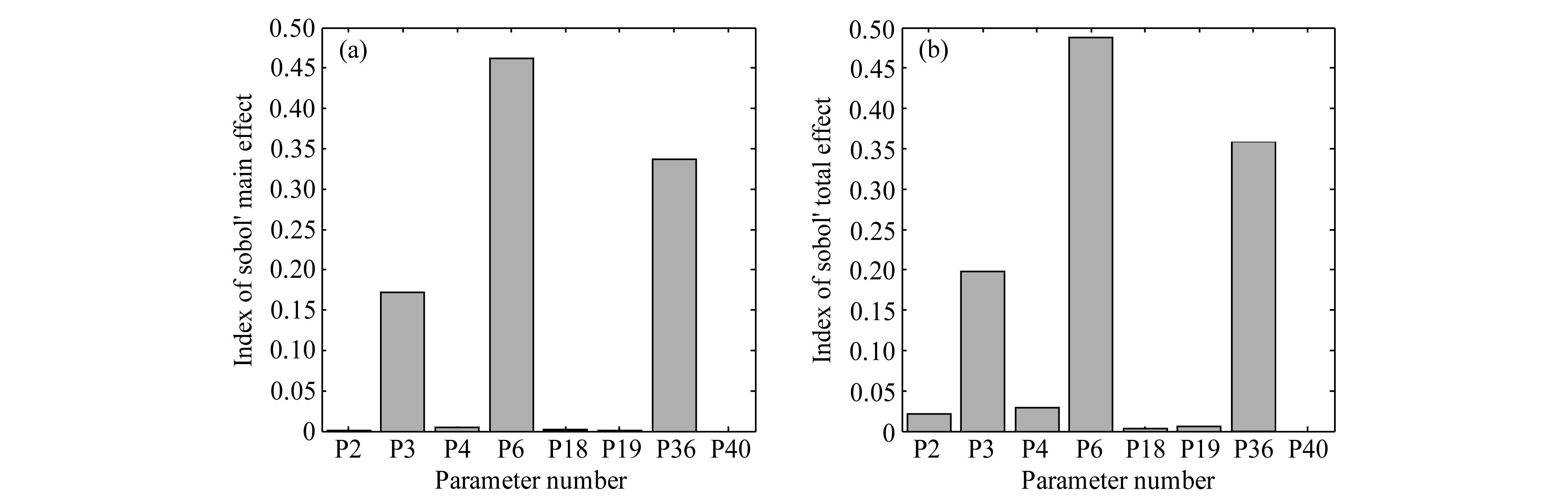图 6 土壤温度的Sobol′(a)主效应与(b)总效应分析结果Fig. 6 The results of Sobol′(a)main effect and (b)total effect analysis for soil temperature

图 7

Fig. 7

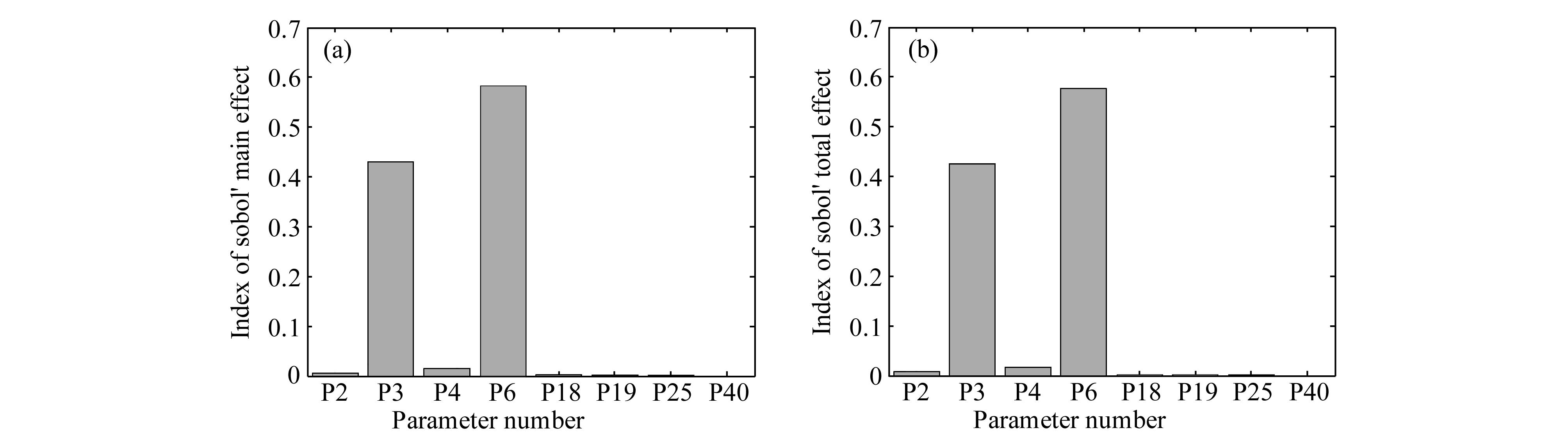图 7 土壤湿度的Sobol′(a)主效应与(b)总效应分析结果Fig. 7 The results of Sobol′(a)main effect and (b)total effect analysis for soil moisture

由分析结果得知，对于土壤温度和土壤湿度，各个参数的主效应和总效应的排名是基本一致的。对 于土壤温度，本研究用总效应分析的结果确定参数的敏感性从高到低的顺序为P6＞P36＞P3＞P4＞P2＞P19＞P18＞P40，而对于土壤湿度，参数的敏感性从高到低的顺序为P6＞P3＞P4＞P2＞P25＞P19＞P18＞P40。显然，P3(土壤孔隙度)、P6(Clapp and Hornbereger “b” 参数)和P36(空气动力学粗糙长度)对于土壤温度起主导作用，经计算累积贡献率达到94.74%；而P3和P6对土壤湿度起主导作用，累积贡献率达到97.38%。

4.3.2 二阶交互效应分析

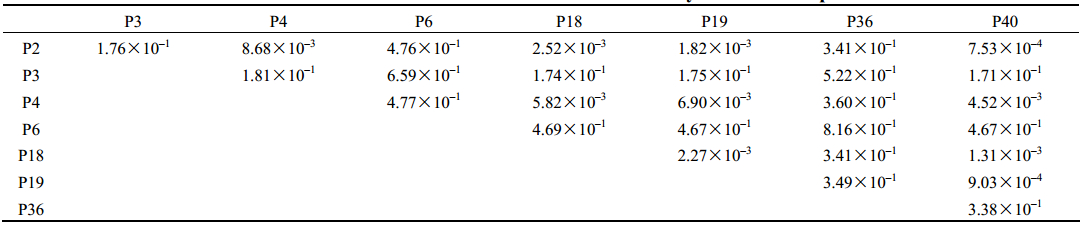
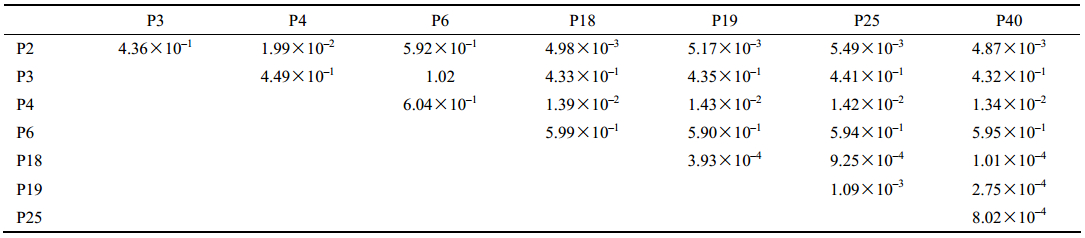
二阶交互效应反映了两个参数对目标的交互影响，两个参数的交互效应越大，说明它们对目标函数的交互影响越大。利用Sobol′ 方法分析二阶交互效应的结果见表 5、表 6和图 8(见文后彩图)。

表 5(Table 5)

表 5 土壤温度的Sobol′ 二阶交互效应分析结果 Table 5 The results of Sobol′ interaction analysis for soil temperature 注：表 5及表 6中的数值即参数间的二阶交互效应Sij=Vij/V。

表 5 土壤温度的Sobol′ 二阶交互效应分析结果 Table 5 The results of Sobol′ interaction analysis for soil temperature

表 6(Table 6)

表 6 土壤湿度的Sobol′ 二阶交互效应分析结果 Table 6 The results of Sobol′ interaction analysis for soil moisture

表 6 土壤湿度的Sobol′ 二阶交互效应分析结果 Table 6 The results of Sobol′ interaction analysis for soil moisture

图 8

Fig. 8

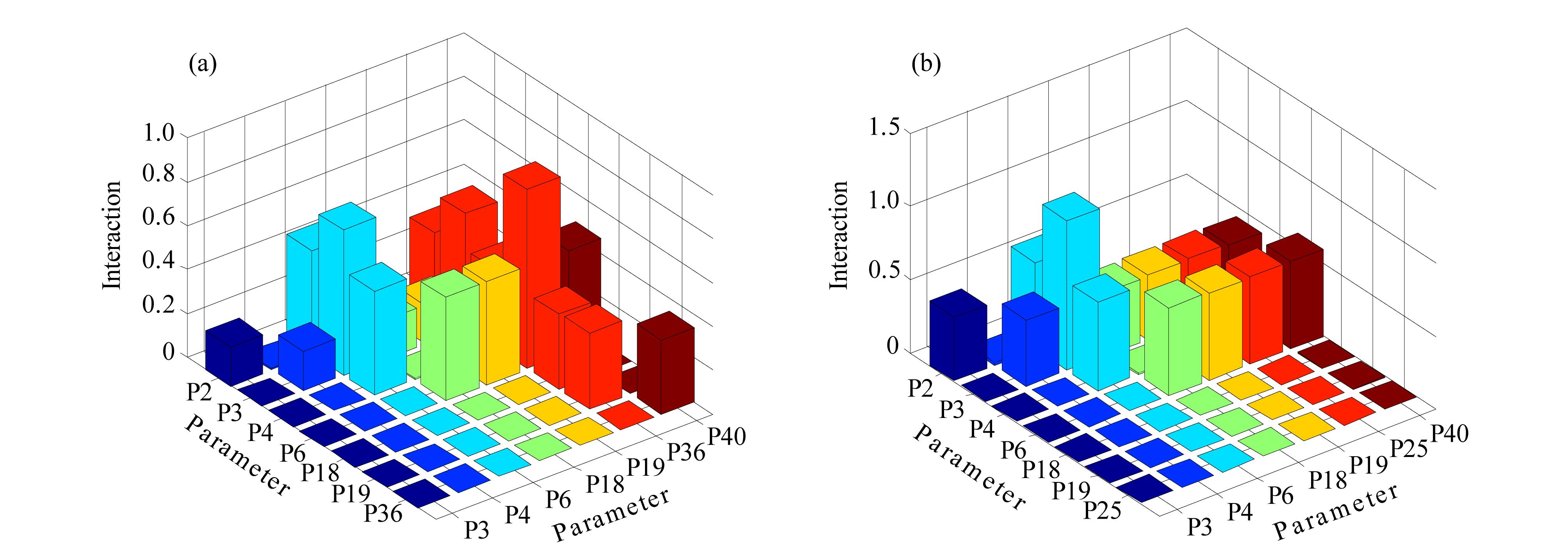图 8 土壤（a）温度和（b）湿度的Sobol′ 二阶交互效应分析结果Fig. 8 The results of Sobol′ interaction analysis for soil (a) temperature and (b) moisture

从表 5得出，对于土壤温度，P3(土壤孔隙度)、P6(Clapp and Hornbereger “b” 参数)和P36(空气动力学粗糙长度)两两的交互效应最强，这三个参数与其他参数之间也存在较强效应。同样的，从表 6得出，对于土壤湿度，P6与其他参数之间都存在极强效应，P3与除P6以外的其他参数之间都存在强效应，P4(最小土壤毛细势)与除P3、P6以外的参数之间都存在中等程度效应。

4.4 筛选出的敏感参数的物理解释

从Morris定性敏感性分析和Sobol′ 定量敏感性分析的结果可知，对于土壤温度，P3(土壤孔隙度)、P6(Clapp and Hornbereger “b” 参数)和P36(空气动力学粗糙长度)是最重要的参数；对于土壤湿度，P3和P6是最重要的参数。事实上，从物理意义的角度出发，P6是计算土壤水力传导率和土壤水势的关键参数，P3是计算土壤体积含水量的重要参数，可见这两个参数在计算土壤湿度的过程中是至关重

要的；而在CoLM计算土壤温度的过程中，土壤湿度是计算土壤热力传导率的关键(因此P3和P6是 重要参数)，而P36(空气动力学粗糙度)是计算感热的重要参数，感热反映了大气与土壤之间的热交换过程，因此P3、P6与P36是计算土壤温度的重要参数。研究表明，筛选结果是合理的，Morris方法可以用极少的样本量筛选出这些最重要的参数。

另外本研究发现，对于土壤温度和土壤湿度，重要参数是基本相同的，从上述的土壤热力传导率的计算过程可知这是合理的结果。两个目标都是土壤相关的变量，因此在未来的参数优化研究中，有望通过优化一组参数来同时提高模式对土壤温度和湿度的模拟水平。

5 结论与讨论

本研究对CoLM模式的40个可调参数进行定性和定量的敏感性分析，找出了对土壤温度和土壤湿度模拟的最敏感参数。研究选用的两个方法，Morris方法是常用的定性参数筛选方法，Sobol′ 方法是常用的定量敏感性分析方法，研究结果表明这两种方法结论一致，而且筛选结果从物理意义也可以解释。

Morris方法和Sobol′ 方法的敏感性指标丰富，可以从多角度考虑，得到可靠的结果，但这两种方法也存在一定的局限性。Morris方法由于筛选过程依赖主观判断，可能过多地筛选参数。而且，不合理地确定参数水平数p和重复次数r可能会导致重复取样，即大样本量和小样本量之间没有区别，所以在使用此方法时需要充分了解它的工作原理；而Sobol′ 方法需要基于较大样本量才能得到可靠的定量敏感性分析结果，所以它并不适用于参数较多的大复杂动力系统模式的参数筛选。

在参数筛选的过程中可能会出现两类错误：第一类是拒真，即忽略了重要参数；第二类是受假，即筛选出不重要的参数。显然，在参数优化问题中，一类错误是更危险的。参数筛选时，Morris方法和Sobol′ 方法在合理的样本量下不会犯第一类错误，而Morris方法由于比较依赖主观判断，容易犯第二类错误。在实际的应用中，要根据研究目的选择最恰当的方法。对于大复杂动力系统模式，因为偏重考虑运算成本的问题，所以推荐使用Morris方法。如果不存在模型运算成本问题，推荐使用Sobol′ 方法，因为只要样本量足够，它得到的结果更具说服力。

本研究实现了大复杂动力系统模式的参数降维，合理地降维可以简化参数间相互作用，提高优化算法的搜索效率，为陆面模式甚至气候模式的参数优化提供科学借鉴，有助于最终提高所关心的模式输出变量的模拟水平。而且，整个过程通过数理统计的知识实现，甚至可以挖掘出潜在的影响目标变量的重要参数，如果再结合物理知识和参数估计的经验，就可以简单高效地优化参数。本研究旨在筛选出对于特定目标变量模拟的重要参数，可以预见此方法也同样适用于区域甚至全球范围。但是，本研究只是通过单点模拟来完成参数筛选，由于区域的特异性，不同区域的参数筛选结果可能存在差异。此外，不同时间尺度下的分析结果也可能存在差异。所以，提高CoLM整体的模拟能力尚需要更多的工作。

致谢 感谢中国西部生态与环境科学数据中心及李新研究员提供的CoLM驱动资料；感谢北京师范大学地理学与遥感科学学院刘绍明老师提供的土壤温度和湿度资料；感谢审稿专家的宝贵意见。