土壤水仅占世界可用水资源总量的很小一部分,但由于土壤水含量难以准确测量,所以利用观测土壤水含量来进行气象模拟是非常不切实际 的,又由于卫星短波频率使得覆盖面积和准确度都难以达到要求,所以直接利用其来进行气象模拟也是不切实际的。因此,利用陆面模式对土壤含水量模拟,影响着热量平衡和水量平衡的计算,并且直接和间接的影响着近地面气象要素的预测起着非常重要的作用,例如陆面和大气之间主要的反馈因素——感热和潜热通量,主要取决下垫面的土壤含水量状况。陆面模式的陆面水文过程就是对水量平衡进行描述的:降水落到地面后一部分被叶面截流,一部分到地面;经叶面截流的部分用于蒸发或滴落到地面,与直接落到地面的降水一起渗入土壤中或形成地表径流;土壤中的水和叶面截流的降水通过蒸发返回大气,植被的根系从土壤中吸收水分再由叶面向大气蒸腾水汽。这样形成了一个大气、陆地水分循环圈。可见陆面水分循环不仅决定了水的分布和平衡,还通过蒸发和降水过程,对能量的再分配起着决定性作用(曹丽娟和刘晶淼,2005)。
产汇流过程在陆面过程的水量平衡中占有重要的地位,直接影响蒸散发、地表径流、壤中流和地下径流的产生,但是在陆面水文过程中对产汇流的部分描述常常过于简单,产汇流的计算误差直接影响这土壤含水量的计算精度,从而会影响着蒸发和陆面水量、热量平衡计算。目前,大多数陆面模式中对产汇流的描述主要存在以下不足:假定网 格内的土壤等的均一性,没有考虑产流的不均匀性,如下渗能力的不均匀性和蓄水容量的不均匀性对产流的影响,缺少网格间径流沿地形汇流的描述。在水文学中,用于模拟和预报径流的水文模型早已存在,有的模型已经广泛应用于我国的洪水预报和径流模拟当中(赵人俊,1984)。因此,可以借鉴水文模型对产汇流的描述,来完善陆面模式的水文过程,以此提高模式对径流的模拟精度,这无疑可以大大改善陆面过程对能量和水分平衡的模拟精度。
GRAPES模式(Global-regional assimilation and prediction system) 由中国气象局于2000年开始组织研究开发的数值预报系统(陈德辉和沈学顺, 2006; 陈德辉等,2008),GRAPES_Meso模式是其区域中尺度数值预报系统版. GRAPES_Meso模式已先后在国家气象中心、广州区域气象中心、上海台风研究所实现业务运行,表现出了较好的预报技巧(薛纪善和陈德辉,2008)。GRAPES_Meso中的陆面模式是NOAH-LSM(Noah-Land Surface Model)模式。但是NOAH-LSM陆面模式对水文过程特别是径流的描述还存在明显不足,即不能完整的描述水文循环过程(Abbott et al.,1986),依据陆面水文过程参数化方案使用的是简单水量平衡模型SWB(Simple Water Balance,Entekhabi et al, 1999)。张万昌、徐精文(徐精文,2009)将XXT模型(Xin’anjiang X TOPMODEL)与NOAH-LSM模式进行耦合研究,取得了良好的应用效果。本文是针对NOAH-LSM模式的不足,对其水文过程做了以下改进:改进产流模块,加入蓄水容量曲线,以此完善了陆面模式对下渗和径流产生这部分水循环的描述;嵌入汇流模块,以弥补GRAPES_Meso陆面模式中缺少汇流模块的缺陷,同时实现逐时步改变格点土壤含水量,使改进后的陆面模式能够模拟完整的闭合水文循环过程,改善土壤含水量在空间和时间上的预报,进而影响近地面气象要素的预报。
2 NOAH-LSM 陆面模式的改进 2. 1 NOAH-LSM 陆面模式的原产流方案
在NOAH-LSM陆面模式中,地表径流参数化方案是用的简单水量平衡模型(Simple Water Balance,SWB)。NOAH-LSM陆面模式中,地表径流方程(徐精文,2009)为:

其中,最大下渗量为:

 为土壤饱和含水率;
为土壤饱和含水率; 为第i层土壤含水率;
为第i层土壤含水率;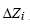 为第i层土壤厚度;Ks是饱和水力传导率;Kdtref=3.0且Kref=2×10-6;δt是模式时间步长(秒)单位为天的值。
为第i层土壤厚度;Ks是饱和水力传导率;Kdtref=3.0且Kref=2×10-6;δt是模式时间步长(秒)单位为天的值。
Noah陆面模式地下产流方案如下面公式所示。
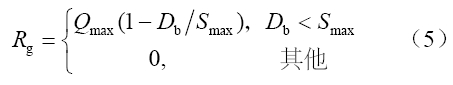
式中,Qmax为最大地下径流量,Smax是土壤水分亏缺的临界值,Db为下层土壤的缺水量,最大值是下层土壤的含水量。
2.2.1 NOAH-LSM陆面模式的原产流方案的问题在降雨过程中,流域上产生径流的部分所包围的面积称为产流面积,是变化的,在降雨开始时,流域中易产流的地区会先产流。由公式(1)和(4)可以看出,NOAH-LSM模型的产流方案只考虑了水的垂向运动,其产流方案使用的是简单水量平衡模型,没有有效地表达径流产源面积的变动情况,因此,需要进一步改进陆面模式的产流方案,提高整体模拟精度。随着GRAPES_Meso模式不断地发展,对预报能力的要求逐渐提高,对其陆面模式中产流过程的描述作也需要进一步的研究。而且对于GRAPES_Meso模式中15 km等这样的计算单元网格,面积与子流域面积大致相等(水利部水文局, 2008),网格内的产流面积是随着降雨时间而不断变化的,因此有必要用新的流域水文模型的产流方案代替简单水量平衡模型,以更好的刻画NOAH- LSM陆面模式中对水文过程的表达,进而改善对近地面气象要素的描述。
2.2.2 NOAH-LSM陆面模式产流方案的改进改进的陆面模式产流方案利用蓄水容量曲线描述单元网格内产流面积的变化。所谓蓄水容量面积分配曲线是:部分产流面积随蓄水容量而变化的累计频率曲线(赵人俊,1984)。应用蓄水容量面积分配曲线可以确定降雨空间分布均匀情况下蓄满产流的总径流量。实践表明,对于闭合流域,流域蓄水容量面积分配曲线采用抛物线型为宜,其线型为

式中,f为产流面积(km2);F为全流域面积(km2);W'为流域单点的蓄水量(mm);WMM为流域单点最大蓄水量(mm);B为蓄水容量面积曲线的指数。
根据流域蓄水容量面积分配曲线及其与降雨径流相互转换关系,改进后的产流方案为:
若 ,即局部产流时,
,即局部产流时,
 式中,P、E分别是网格降水量(mm)、网格蒸发量(mm)
式中,P、E分别是网格降水量(mm)、网格蒸发量(mm)  。
。
若  ,即全网格产流时,
,即全网格产流时,

式中,W0为流域初始土壤蓄水量(mm);WM为流域平均最大蓄水容量(mm);R为总径流量(mm)。
地下产流方案与原NOAH-LSM方案相同。
2.3 NOAH-LSM陆面模式增加的汇流方案降雨所产生的地表径流会随地形进行汇流运动,如果缺少汇流过程的描述,就无法考虑坡面径流在水平二维方向的水量再分配,不能较精确地刻画陆面及浅地表水循环,会使所产生的径流在其所生成的网格内继续蓄积,从而违背了重力作用,不符合真实的流域情况。在陆面模式中,地表径流影响着陆—气反馈的重要因素感热通量和潜热通量。通过加入汇流模式后,NOAH-LSM陆面模式中加入对水平二维地表径流的描述,更加符合真实的流域汇流。
NOAH-LSM陆面模式中增加的汇流方案选取Muskingum(Bates and De Roo,2000)汇流方法。在Muskingum方法中,采用逐栅格的Muskingum汇流方法将地表径流演算至流域出口。以地表径流Qs为例,a、b、c三个栅格的流量分别为Qa、Qb、Qc。栅格a、b、c的水流均流向栅格d,流至栅格d的流量分别为Q'a、Q'b、Q'c,可以通过Muskingum-Cunge方法(王莉莉等,2007)计算得到。因此,栅格d的总出流量可表示为。

式中,Q'd为栅格d自身栅格内降水产流量。
3 试验结果及分析
为了充分验证原NOAH-LSM陆面模式和改进的NOAH-LSM陆面模式在的模拟效果,本研究选取2008年8月1日08时(北京时间,下同)至10月1日08时的降水进行模拟试验,预报时长为24 h,以每日08时进行滚动预报,试验覆盖区域为(15°~64.5°N,70°~145.3°E)。
本次试验将分辨率为1°×1°的美国NCEP全球预报场作为初始场和侧边界条件,驱动15 km×15 km的GRAPES_Meso模式和改进后的GRAPES_ Meso模式,由于资料限制,本次试验选取土壤湿度、2 m温度等近地面要素,进行模拟计算,其中土壤湿度观测站点和2 m温度等近地面要素观测站点的布设不同。
3.1 土壤含水率和原NOAH-LSM陆面模式相比,改进后的模式不仅考虑到水量垂向变化,而且考虑到了水平二维方向上的水分再分配,坡面流改变了土壤湿度的水平梯度分布,陆面水循环首先引起了土壤湿度的改变,选取南充和临汾两个站点10 cm深度的土壤含水率进行对比,站点经纬度和所属流域见表 1,其中南充站观测土壤含水率起始时间是8月10日08时(图 1a),原GRAPES模式模拟的土壤含水率 模拟与观测值相比偏小,改进陆面模式后模拟的土壤含水率比观测值偏大,但与原GRAPES模拟结 果相比更接近。临汾站点观测的10 cm土壤含水 率起始时间为8月1日08时,站点的土壤含水率从3日08时开始就达到饱和,并一直持续到9月30日08时(图 1b),原GRAPES模拟结果明显偏小,改进后的GRAPES模拟结果与实测值较为接近。证明了改进产流方案并嵌入汇流模块后,模 式考虑到流域内径流沿水系汇流对土壤含水率的影响。
| 表 1 站点经纬度 Table 1 Latitudes and longitudes of the stations |
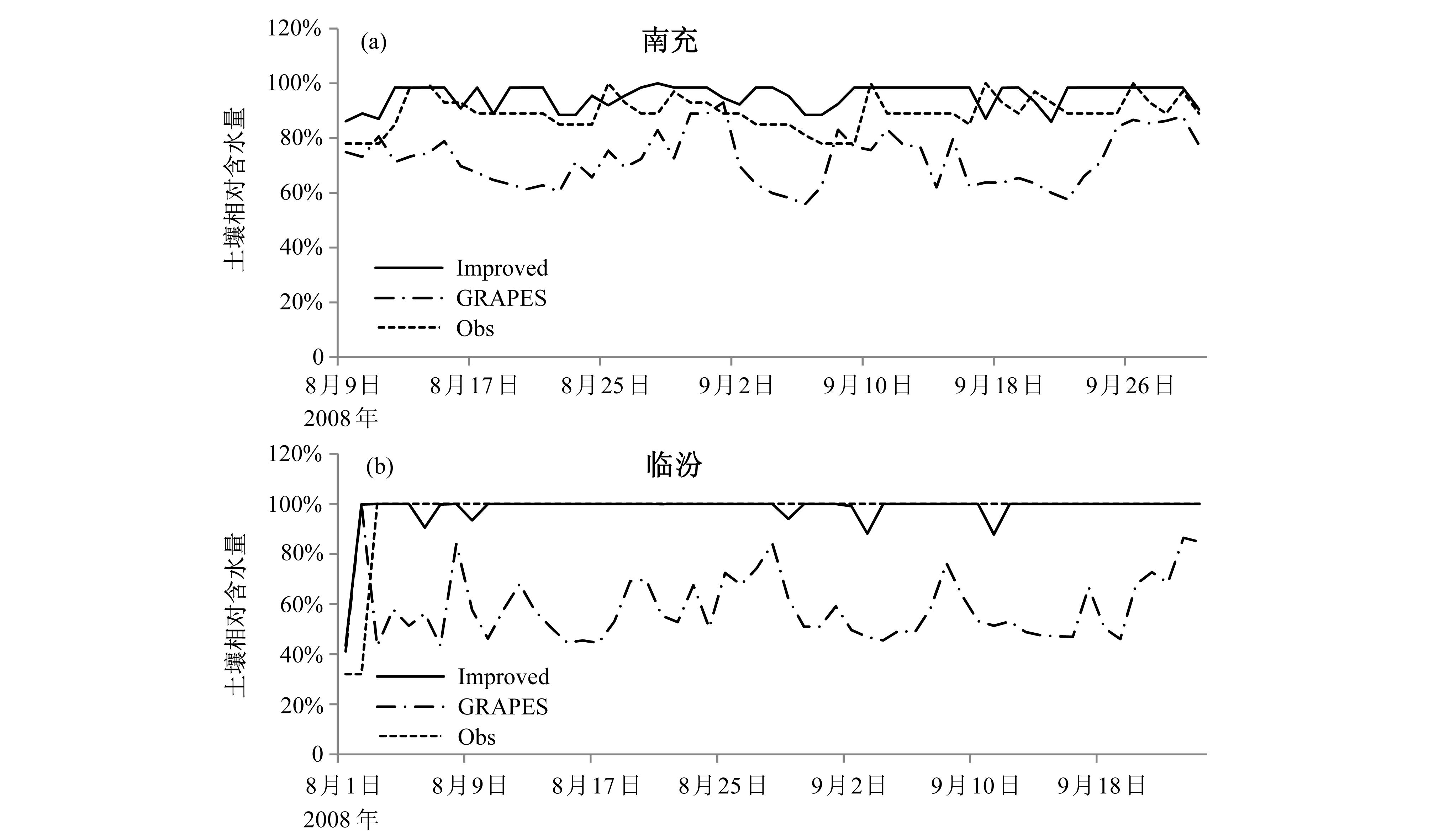 | 图 1 10 cm 土壤含水率Fig. 1 Soil moisture content at 10 cm |
土壤含水量的变化直接影响土壤温度,进而影响到2 m温度的变化。本次选取寿县、商丘和麻城三个站点(表 2),对其模拟的2 m 温度和实测值进行对比,见图 2,原GRAPES模式与改进后模式模拟结果相差不大,改进后的累积误差稍小于原GRAPES的累积误,从表 3可以看出改进后模式的均方根误差也小于原GRAPES模式模拟的,三个站点的均方根误差都在0.30~0.40。证明了基于GRAPES陆—气双向反馈模式加入汇流模块后,考虑了流域内地表径流、壤中流和地下径流在水平二维方向的运动,对2 m温度有一定的影响,但是每个站点的模拟效果不尽相同,这是和站点所属的流域位置以及站点降水的大小有关。
 | 图 2 2 m温度Fig. 2 Temperature at 2 m |
| 表 2 站点经纬度 Table 2 Latitudes and longitudes of the stations |
| 表 3 2 m温度均方根误差 Table 3 Root-mean-square error of temperature at 2 m |
土壤湿度的变化通过也影响到10 m 风速的模拟,本节选取三个站点(见表 2)对10 m 风速的模拟值和观测进行对比。从图 3可以看出改进模式后模拟的过程线与原模式模拟的过程线相差不大,从表 4均方根误差来看,改进后的模式略好与原GRAPE模式,对于均方根误差,改进后模式和原GRAPES模式误差在2.4~3.0。
 | 图 3 10 m风速Fig. 3 Wind speed at 10 m |
| 表 4 10 m风速均方根误差 Table 4 Root-mean-square error of wind speed at 10 m |
本次研究选取TS评分进行降水检验,TS评分作为对确定性预报的评分标准,已经纳入了业务预报评价体系(黄卓,2001)。选取2513个降水自动站站点,进行预报降水检验。从表 5中2008年8月和9月的TS评分结果上,基于GRAPES陆—气双向反馈模式的降水评分结果和原GRAPES降水评分相差不大。如表 6所示,选取两个站点观测降水与模式模拟降水进行对比,如图 4,基于GRAPES陆—气双向反馈模式与原模式相比对降水落区的预报有了一定变化。
| 表 5 TS评分和预报偏差B Table 5 Threat Score (TS) and Bias error (B) |
| 表 6 站点的经纬度 Table 6 Latitudes and longitudes of the stations |
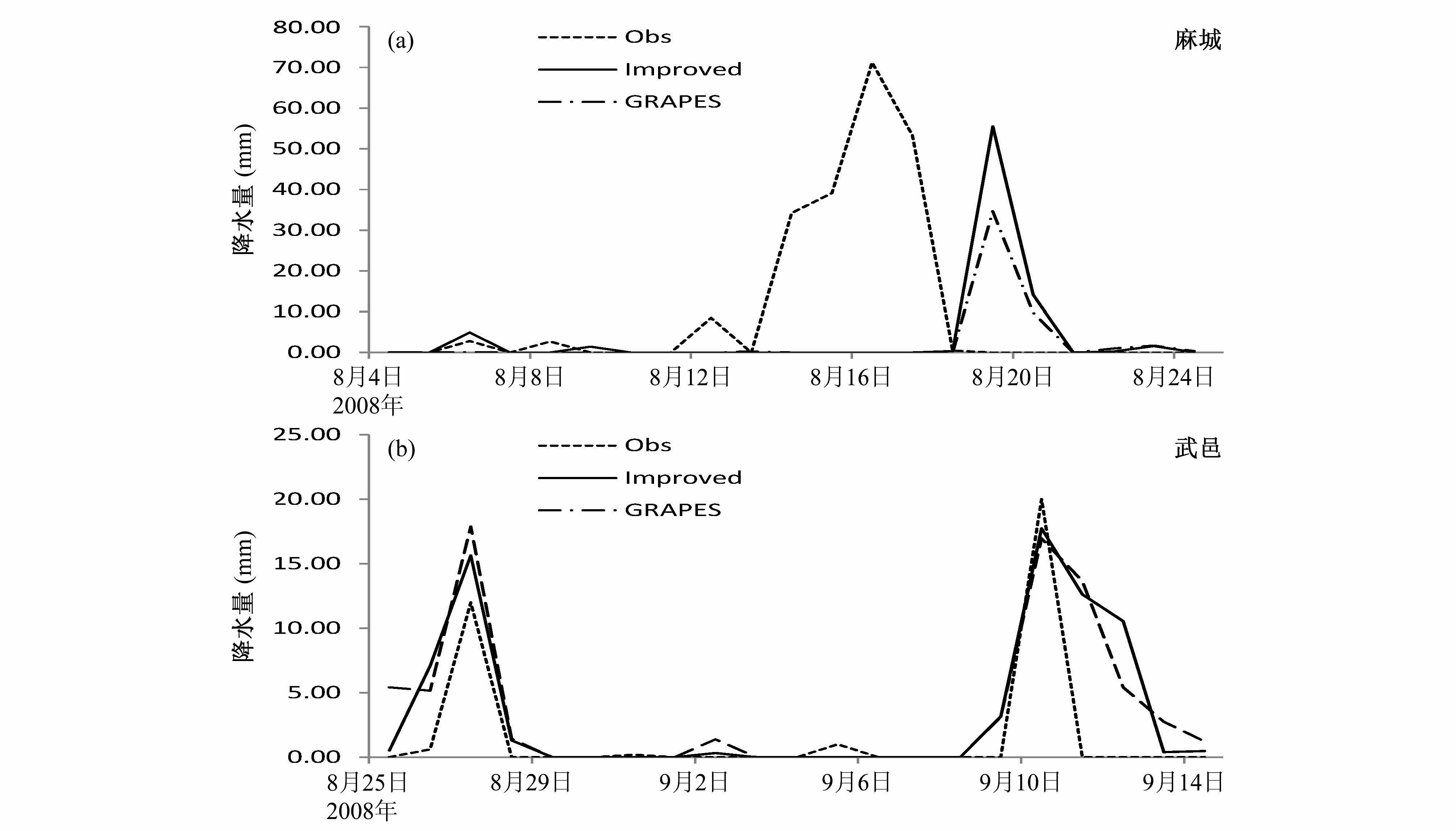 | 图 4 观测降水和模拟降水Fig. 4 Observed and simulated precipitation |
由于初始场资料的限制,对王家坝站8月13日20时到16日20时的流量进行对比,如图 5,改进陆面模式后模拟的流量过程与原模式相比有了较大的改进,也更加接近实测流量过程,这说明改进的NAOH-LSM陆面模式能够进行流量模拟。
 | 图 5 2008年8月13~16日流量Fig. 5 Discharge from 13th to 16th Aug 2008 |
本试验介绍了GRAPES NOAH-LSM陆面模型产流方案的原理,针对原NOAH-LSM陆面模型建模型时,考虑产流机制比较简单,对其产流模块,进行了必要改进,加入了蓄水容量曲线,以考虑网格内土壤含水量分布不均的情况,并加入了汇流模块对地表二维水流的描述,以弥补原GRAPES无法模拟流量的缺陷。
选取2008年8月至9月降水进行模拟试验,结果表明改进后的模式,引起了近地面气象要素的变化,对于10 cm土壤含水率,改进后模式模拟结果与观测值较为接近,土壤含水率的增加也使得2 m温度和10 m风速的模拟结果和观测值较为接近,从均方根误差来看,改进后的模式略好于原GRAPES模式。与原GRAPES模式相比,能够将降水对土壤湿度的影响作用到径流的模拟上,并且通过产、汇流等陆面水循环的影响反馈到降水的预报中。
然而,改进NOAH-LSM陆面模式还需要对不同的区域进行模拟试验,以便更好地确定不同区域的参数方案,改善GRAPES模式近地面气象要素的预报性能,同时为改进后的NOAH-LSM陆面模式在全球模式以及气候模拟方向上拓展应用做进一步的研究。
| [1] | Abbott M B, Bathurst J C, Cunge J A, et al. 1986. An introduction to the European Hydrological System—System Hydrologique European, "SHE". 1: History and philosophy of a physically-based, distributed modelling system[J]. J. Hydrol., 87: 45-59. |
| [2] | Bates P D, De Roo A P J. 2000. A simple raster-based model for flood inundation simulation[J]. J. Hydrol., 236: 54-77. |
| [3] | 曹丽娟, 刘晶淼. 2005. 陆面水文过程研究进展[J]. 气象科技, 33 (2): 97-103. Cao Lijuan, Liu Jingmiao. 2005. Review of land-surface hydrological process studies[J]. Meteorological Science and Technology (in Chinese), 33 (2): 97-103. |
| [4] | 陈德辉, 沈学顺. 2006. 新一代数值预报系统GRAPES研究进展[J]. 应用气象学报, 17 (6): 773-777. Chen Dehui, Shen Xueshun. 2006. Recent progress on GRAPES research and application[J]. Journal of Applied Meteorological Science (in Chinese), 17 (6): 773-777. |
| [5] | 陈德辉, 薛纪善, 杨学胜, 等. 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J]. 科学通报, 53 (20): 2396-2407. Chen Dehui, Xue Jishan, Yang Xuesheng, et al. 2008. New generation of multi-scale NWP system (GRAPES): General scientific design[J]. Chinese Science Bulletin, 53 (22): 3433-3445. |
| [6] | Entekhabi D, Asrar G R, Betts A K, et al. 1999. An agenda for land surface hydrology research and a call for the second international hydrological decade[J]. Bull. Amer. Meteor. Soc., 80: 2043-2058. |
| [7] | 黄卓. 2001. 气象预报产品质量评分系统[G]. 北京: 中国气象局预测减灾司, 9-11. Huang Zhuo. 2001. Weather forecasting product quality rating system (in Chinese)[G]. Beijing: Department of Prediction and Disaster Mitigation, China Meteorological Administration, 9-11. |
| [8] | 水利部水文局. 2008. 水文情报预报规范, GB/T22482-2008[S]. 北京: 中国标准出版社. Bureau of Hydrology of the Ministry of Water Resources of the People's Republic of China. Standard for Hydrological Information and Hydrological Forecasting, GB/T22482-2008 (in Chinese)[S]. Beijing: China Standard Publishing House. |
| [9] | 王莉莉, 李致家, 包红军. 2007. 基于DEM栅格的水文模型在沂河流域的应用[J]. 水利学报, 37: 417-422. Wang Lili, Li Zhijia, Bao Hongjun. 2007. Application of hydrological models based on DEM in the Yihe basin[J]. Journal of Hydraulic Engineering (in Chinese), 37: 417-422. |
| [10] | 徐精文. 2009. 基于蓄水容量曲线和TOPMODEL概念的流域水文模型构建及其与Noah LSM的耦合研究[D]. 中国科学院博士学位论文, 42-50. Xu Jingwen. 2009. Development of a basin hydrological model based on soil moisture storage capacity distribution curve integrated with TOPMODEL concept and its coupling with the Noah LSM[D]. Ph. D. dissertation (in Chinese), Chinese Academy of Sciences, 42-50. |
| [11] | 薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用[M]. 北京: 科学出版社, 334-335. Xue Jishan, Chen Dehui. 2008. Scientific Design and Application of Numerical Prediction System GRAPES (in Chinese)[M]. Beijing: Science Press, 334-335. |
| [12] | 赵人俊. 1984. 流域水文模拟——新安江模型与陕北模型[M]. 北京: 水利电力出版社, 23-35. Zhao Renjun. 1984. Watershed Hydrological Model—Xin'anjiang Model and Shanbei Model (in Chinese)[M]. Beijing: Water Power Press, 23-35. |
 2013, Vol. 37
2013, Vol. 37


