2. 南京信息工程大学气象灾害预报预警与评估协同创新中心, 南京 210044
2. Collaborative Innovation Center on Forecast and Evalution of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044
台风具有明显的螺旋波云带结构,而对螺旋波云带传播问题的研究一直是学术界的难题。Chen and Yau(2000)利用MM5模式模拟一个非对称的台风,发现位涡带与云带在分布形势上具有一致的联系性。早期的研究者利用重力波来解释台风内部螺旋雨带的生成及发展机制(Willoughby,1978a,1978b; Xu,1982),Willoughby(1978a,1978b),提出了重力内波理论,Pierce and Fairlie(1993)认为中尺度波动与其说是动量传播的结果,不如说是混合重力惯性波Inertial-gravity waves)的作用更加合理。许多研究者还研究了重力惯性波和天气尺度系统之间的联系(Stato,1989,1993; Chan et al.,1991; Eckermann and Voncent,1993)。重力惯性波可以使 得平流层与对流层之间发生能量的交换。作为重力波另一种形式,重力惯性波在大气中是普遍存在的,在对流层高层和平流层低层表现得尤其明显,重力惯性波的垂直波长较短,波动的固有频率与科氏参数的频率相接近(Barat,1983; Tanaka and Yamanaka,1984; Thomas et al.,1992; Sato,1994)。 Li et al.(2007)研究与台风雨带降水相联系的台风重力惯性波,指出波动的水平尺度较大,波长500~1000 km。结合台风Matsa对台风重力波进行模拟,结果表明台风重力波主要位于台风外围( ChenD et al.,2011)。重力惯性波作为能量传播的一种形式,解 释台风内部螺旋云带波动机制时存在着严重的缺陷,即波动传播的速度与台风内部螺旋波云带传播的速度不符,即重力惯性波的传播波速偏大。之后对台风内部波动的研究转向大尺度的Rossby波。Macdonald(1968)提出类Rossby波后,基于实际观测和模拟资料进行了大量研究。涡旋Rossby波的概念在1997年被提出(Montgomery and Kallenbach,1997; Mon-tgomery and Lu,1997),Chen and Yau(2000)通过数值模拟发现台风中存在一个关键的半径,在该半径处,涡旋Rossby波与基流的相互作用是最强的。从最初的准线性无辐散对称平衡方程模式到正压非对称平衡模式,再到三维准地转模式和三维非对称平衡模式(Michael et al.,1998; Möller and Montgomery,1999,2000),基于台风内部涡旋Rossby波的研究不断加深。张立凤和张铭(1999)针对斜压切变基流中的横波型扰动的波动特征进行了分析,指出在中尺度系统中涡度和散度具有同样的量级,涡旋运动是不可忽视的,涡旋波与重力波同样重要。目前对涡旋Rossby波的特征及动力学机理做了全面的介绍(余志豪,2002),承认涡旋Rossby波对热带气旋的动力结构具有重要作用,但在热带气旋整个周期中所扮演的角色尚不清楚。黄泓和张铭(2003)通过计算特征值问题,指出正压涡旋中的螺旋波的相速度为正值,波动是沿逆时针旋转的。沈新勇等(2005a,2005b)利用Boussinesq近似,在考虑基流存在二次切变的条件下,得出在中尺度暴雨系统中也存在涡旋Rossby波,该波动能量是频散的,相速度与纬向波数有关,结合绝对涡度守恒,导出了中尺度暴雨系统中的涡旋Rossby波的形成机制,并合理解释了涡旋Rossby可能是中尺度暴雨系统发生发展的物理机制。沈新勇等(2007)指出台风涡旋系统中存在正压涡旋Rossby波和斜压涡旋Rossby波,并结合台风云娜对其内部的这两种类型波动进行了特征分析。
台风行星边界层对于台风暴雨的发展和维持具有重要的作用,Michael(1998)发现在边界层附 近,台风特征螺旋雨带具有中尺度和对流尺度的特征,雨带是由线性的胞状反射单体组成,边界层对台风雨带的结构造成了一定的影响,同时边界层风场也受到雨带的影响。而对于海上的热带气旋,强风会在海上的大气边界层中产生大量的水花,水花的蒸发可以在大气和海洋之间传送能量,并且对边界层的结构、积云对流和热带气旋的发展产生一定的影响(Wang et al.,2001)。Tang and Tan(2006)利用单层边界层模式对登陆的热带气旋的边界层风场结构进行了分析,发现径向和切向的水平风场均存在非对称性,径向风在近岸一侧较大,切向风在远离岸的海上较大。随着登陆的深入,切向风减小,径向风增大,最大切向风半径减小,但台风对边界层的反馈效应尚未研究。Wu et al.(2009)用MM5模式研究了登陆过程中地形和地表性质对台风眼墙演变的影响。模拟表明台风谢柏登陆后眼墙的断裂是由地表摩擦的增强导致的。随着内眼墙中的对流消散,台风外眼墙呈现轴对称结构。虽然凝结潜热是环状位涡结构维持的关键因子,但地表摩擦的作用却是双倍的,地表摩擦使得眼墙的位涡消散、伸缩变形,使得环形位涡变得更加狭窄。丁一汇和沈新勇(1998)采用奇异摄动法对粘性条件下的线性不稳定进行了理论上的分析,指出在中尺度对称不稳定中,粘性摩擦对短波和长波衰减最厉害。沈新勇和丁一汇(1998)利用包含粘性的中尺度对称扰动波包的动力学方程组,得出粘性耗散导致扰动随时间呈指数衰减的结论。可见,边界层的粘性摩擦对中尺度台风系统的影响是不容忽略的。研究粘性摩擦对台风波动结构的影响是很有意义的。
高度概括的理论模型往往做了很大程度的简化,它虽然可以揭示台风波动的一些特征和机制,但无法详细具体地考虑粘性摩擦或热量的源、汇项对台风波动特征所造成的影响。本文利用高分辨率的中尺度数值模式的输出结果,采用包含摩擦项的动力学方程组,通过求解特征值问题,对粘性摩擦在台风麦莎的正压特征波动中所造成的影响进行了分析。
2 台风麦莎数值模拟
2005年9号台风麦莎(Matsa)于7月31日12时(协调世界时,下同)在菲律宾以东的西北太平洋洋面上生成,8月9日06时消亡,历时近9天。期间4日12时强度最大,中心气压950 hPa,最大风速45 m/s。麦莎于5日19时登陆浙江省玉环县干江镇,登陆时中心气压和风速分别是950 hPa和45 m/s。登陆后台风中心继续向西北方向移动,沿途先后经历了海岸地形,山脉地形等,地形高度最高为800 m左右,持久的强陆地摩擦作用对台风麦莎产生了很大的影响。本文采用中尺度模式WRF,模拟台风麦莎从最大强度(4日12时)到登陆后一直北上进入山东半岛(8日00时)的过程。初始场资料为6小时时间间隔、分辨率为1°×1°的NCAR(National Centers for Atmospheric Research)/NCEP(National Centers for Environmental Prediction)再分析资料和SST(Sea Surface Temperature)资料。三重双向嵌套网格(第三重网格为移动网格),格距分别为18 km、6 km、2 km,积分步长60 s,垂直方向46层。
图 1a是实况和模拟的台风麦莎的路径对比图,模拟路径与实况非常接近,误差不超过50 km。图 1b比较了模拟和实况的台风中心最低气压和地面最大风速。模拟的前24 h,台风的强度与实况较吻合。24 h后由于麦莎登陆,下垫面性质的改变,使得模拟结果与实况的偏差加大,但就整体而言,模式很好地模拟和再现了台风麦莎的强度变化趋势。考虑到台风麦莎实际影响半径达1000 km以上,为了对其整个结构进行系统的研究,且考虑粘性摩擦的影响,我们采用6日15时D01 的模拟数据资料进行下一步的分析。 | 图 1 观测和模拟的(a)台风移动路径及(b)最低气压(单位:hPa)和最大风速(单位:m/s)。实线为观测,虚线为模拟Fig. 1 The observed and simulated(a)typhoon tracks and (b)minimum pressure(hPa) and maximum wind speed(m/s). Solid and dashed lines denote observation and simulation,respectively |

上述方程组中,u=dr/dt,ν=rdλ/dt分别表示空气质点的径向速度和切向速度,h表示自由面的高度或者水的深度,Δ为柱坐标系中的拉普拉斯(Laplace)算子, ,ν为摩擦系数,取值为1.46×10-5s-1;K为牛顿冷却系数,取值为6×10-6s-1(李崇银和李桂龙,1996)。由于台风属于中尺度天气系统,采用f平面近似,f取为常数。
,ν为摩擦系数,取值为1.46×10-5s-1;K为牛顿冷却系数,取值为6×10-6s-1(李崇银和李桂龙,1996)。由于台风属于中尺度天气系统,采用f平面近似,f取为常数。
假定基本物理变量具有径向上的切变,即 。对以上方程组(1)~(3)进行线性化处理,将
。对以上方程组(1)~(3)进行线性化处理,将 代入到以上方程组(1)~(3)中,得到如下的线性化小扰动方程组:
代入到以上方程组(1)~(3)中,得到如下的线性化小扰动方程组:

对该扰动方程组(4)~(6)中的物理量求特征波解,令 ,m为沿着切向(或者绕圆周方向)的波数,ω为波动的圆频率,通常为复数ω=ωr+iωi,实部ωr是波动传播速度有关的参数。虚部ωi是波动增长率,ωi>0表示波动振幅随时间增长,波动不稳定;ωi<0 则波动振幅随时间衰减。将扰动量的波动形式带入扰动方程,得到如下的常微分方程组:
,m为沿着切向(或者绕圆周方向)的波数,ω为波动的圆频率,通常为复数ω=ωr+iωi,实部ωr是波动传播速度有关的参数。虚部ωi是波动增长率,ωi>0表示波动振幅随时间增长,波动不稳定;ωi<0 则波动振幅随时间衰减。将扰动量的波动形式带入扰动方程,得到如下的常微分方程组:

下面将依据上述常微分方程组讨论台风麦莎的 正压波动情况,考虑到台风麦莎中包含了不同性质的波动,不同性质波动的发生发展的条件是不同的,因此结合相应的简化及假设,分情况讨论粘性摩擦对台风麦莎的正压波动结构及稳定性的影响。
4 不考虑径向基本气流,只考虑切向基本气流为线性切变的情况
在不考虑径向基本气流,只考虑切向基本气流为线性切变的情况下,只有沿着切向圆周方向 传播的重力惯性外波;且不考虑径向基本气流时, ,那么方程(4)的平均方程还是满足梯度风平衡关系:
,那么方程(4)的平均方程还是满足梯度风平衡关系:  。
。
4.1 常微分方程组简化及数值差分方法
在常微分方程组(7)~(9)之中,令 ,假定切向基本气流
,假定切向基本气流 在径向方向具有线性切变,即
在径向方向具有线性切变,即 (其中系数a确定的方法如下:考虑在最大风速层高度上,先将实际的切向基本气流沿着方位角方向进行平均,得到实际的沿着方位角方向平均的切向基本气流
(其中系数a确定的方法如下:考虑在最大风速层高度上,先将实际的切向基本气流沿着方位角方向进行平均,得到实际的沿着方位角方向平均的切向基本气流![]() ,再根据面积相等原则,确定
,再根据面积相等原则,确定![]() 。在假设径向基本气流为零的情况下,方程满足梯度风平衡关系,因此得到
。在假设径向基本气流为零的情况下,方程满足梯度风平衡关系,因此得到 ,其中
,其中 为台风中心的高度,即研究所选取等压面上台风中心所在的等高线的数值。如此在考虑切向基本气流为线性切变的情况下,常微分方程组(7)~(9)简化为:
为台风中心的高度,即研究所选取等压面上台风中心所在的等高线的数值。如此在考虑切向基本气流为线性切变的情况下,常微分方程组(7)~(9)简化为:

6日15时台风麦莎登陆浙江省,台风主体大致分布在陆地上。考虑到该时刻台风影响区域的最高地形高度不超过800 m,而边界层高度在1 km以下,所以为了在考虑摩擦作用的同时,避免受到地形的影响,我们取800 m高度层进行研究。这样将台风简单化为某一层的正压结构。
地转参数f = 6.3230314726×10-5(纬度为30.51°N),选取台风中心高度 的具体方法,提取800 m高度相对应的等压面上的等高线数据,由该等压面上台风中心的等高线数据来确定
的具体方法,提取800 m高度相对应的等压面上的等高线数据,由该等压面上台风中心的等高线数据来确定 =446m。考虑到台风中心的风速几乎为静风,最外围的台风环流很弱,与台风环流相联系的切向风很弱,于是给定内外(台风中心和台风最外围)边界条件:
=446m。考虑到台风中心的风速几乎为静风,最外围的台风环流很弱,与台风环流相联系的切向风很弱,于是给定内外(台风中心和台风最外围)边界条件:

求解(10)~(12)式特征值的差分方法如下:以台风中心为圆心,在径向方向上沿半径等间距取57个格点,格距18 km,差分区域的最大半径为1008 km。总57个格点中,称n=1,3,…,2k+1,…, 55,57为奇数点,n=2,4,…,2k,…,54,56为偶数点,所求变量采用交叉网格分布(图 2),即变量V分布在奇数点上,编号为V1,V3,…,V2k+1,…,V55,V57;变量U、H分布在偶数点上,编号为U2,H2,U4,H4,…,U2k,H2k,…,U54,H54,U56,H56。
 | 图 2 交叉网格上变量的分布Fig. 2 Distributions of variables at grids |
满足边界条件取V1=0,V57=0; 采用前、后插计算,其他格点处的
采用前、后插计算,其他格点处的 ,dU/dr,dV/dr,dH/dr,采用中央差,d2U/dr2,d2V/dr2,d2H/dr2采用三点式差分方案。
,dU/dr,dV/dr,dH/dr,采用中央差,d2U/dr2,d2V/dr2,d2H/dr2采用三点式差分方案。
差分后的方程组离散化为矩阵:AX=ωBX,其中A为83×83阶复矩阵,B为83×83阶实数单位矩阵,ω为特征值,X为特征向量。求解特征值和特征向量就可以得到不稳定扰动的增长率、相角速度和相应的扰动结构,下面我们分析该情况下粘性摩擦对台风麦莎的波动结构及其稳定性所造成的影响。
4.2 粘性摩擦对波动结构特征和稳定性的影响
为研究考虑粘性摩擦后在切向基本气流为线性切变情况下,台风麦莎内部重力惯性外波稳定性的变化情况,我们给出相角速度ωr/m和增长率ωi随波数的变化图(图 3a,其中波数m=1~200)。同时给出了无摩擦与有摩擦情况下的波动增长率的差值直方图(图 3b)。
 | 图 3(a)相角速度ωr/m(单位:10-4 s-1)和增长率ωi(单位:10-4 s-1)以及(b)波动增长率差值(无摩擦减去有摩擦)随波数的变化Fig. 3(a)The phase angular velocity(ωr/m) and growth rate(ωi) and (b)difference between growth rates with and without friction as the function of wave number |
图 3a表明粘性摩擦下的重力惯性波增长率ωi曲线为单峰曲线,在波数m=45左右取得最大值(ω45=1.070×10-3s-1),即最不稳定重力惯性波的波数为45左右。将无摩擦时的波动增长率减去考虑摩擦后的相对应波数的波动增长率,我们得到了波动增长率的差值直方图(图 3b),从图中可以看到,在波数m=1~200中,除少数波数外,整体上波动受到粘性摩擦的影响后,波动增长率明显减小,波动较无摩擦的情况相对稳定,特别注意的是m=1波时,这种在粘性摩擦的影响下波动得到衰减的现象最为显著,这也是我们在下文中选择m=1 波进行研究的依据之一。可见粘性摩擦使得重力惯性波衰减。相角速度ωr/m乘以波动半径r=1000 km便可得到波动的传播速度,速度均为正值,表明波动是沿逆时针方向传播的。此外,在波数m>35,波动传播速度变化较为缓慢,平均传播速度为33.73 m/s,当波数m<35时,波动的传播速度随波数的减小而增大,波数m=1时传播速度增加到47.43 m/s。为研究该情况下,粘性摩擦对台风麦莎内部重力惯性外波的波动结构产生怎样的影响,我们对波数在1~200的波动都进行了研究,得出的关于波动的性质结论是一致的,因此考虑到不失一般性且尽可能的简单明了,本文以最简单的切向波数m=1为例进行分析。下面给出m=1时的台风麦莎有摩擦的扰动高度场与扰动风矢量场的叠加图(图 4)和相应的扰动散度场和扰动散涡比(扰动散度/扰动涡度)(图 5)。
 | 图 4 有摩擦情况下扰动高度(单位:m)场、扰动风矢量(单位:m/s)场的叠加图Fig. 4 Horizontal disturbances of disturbed height(m) and wind vectors(m/s)with friction |
 | 图 5 有摩擦情况下(a)扰动散度场和(b)扰动散涡比场Fig. 5 Horizontal disturbances of perturbed(a)divergence and (b)divergence-vorticity ratio with friction |
考虑摩擦存在时(图 4),台风中扰动高度场的分布形式是以某一直径为对称轴的反位相对称结构,即在同一半径圆上扰动高度场呈正、负位相分布,体现1波的波动结构,扰动高度场h'、扰动风矢量场(u'v')的波动形式大体上仍然具有重力惯性外波的性质,即波动风矢量基本垂直于波动高度场,波动的明显区域位于台风的外围,且扰动风场以径向分量为主。从图 5(a)以及没有摩擦时的扰动散度场(图略)可见,无论是否考虑摩擦,重力惯性波中散度的扰动量值在台风外围最大,这与扰动高度场跟扰动风场的大值区域是相对应的,说明在台风外围和重力惯性波相联系的辐合辐散运动是重要的。此外分别计算了有摩擦时的扰动散度对扰动涡度的比值(图 5(b))以及没有摩擦时的扰动散涡比(图略),发现在整个台风范围内散涡比的绝对值均在2以上,即对于重力惯性波而言,辐合辐散占主导地位。
为更加精确地认识摩擦究竟对重力惯性波造成多大的影响。即扰动风场和扰动散度场的变化是怎样的,我们用有摩擦的扰动风场减去无摩擦的扰动风场,得到扰动风场的差值,绘制出图 6的扰动风场差值矢量图,考虑粘性摩擦存在后,在半径 r<800 km范围内,扰动风差值的矢量方向与无摩擦时风矢量的方向基本相反,粘性摩擦使得扰动的径向风分量减弱;在r>800 km的台风外围,摩擦的存在使得扰动径向风分量加强。扰动散度的比值图(图 7a)(考虑粘性摩擦的扰动散度除以不考虑粘性摩擦的扰动散度)表明,与重力惯性外波相联系的辐合辐散运动在r<600 km范围内呈减弱趋势,而在r>600 km的外围,由于边界层摩擦的存在,使得扰动散度增大,即辐合辐散运动会增强;该结论在扰动散涡比的比值图(图 7b)(考虑粘性摩擦的扰动散涡比除以不考虑粘性摩擦的扰动散涡比)上同样表现出来,比值的大小代表着粘性摩擦对散涡比的影响,比值绝对值在1以上,表明由于边界层摩擦的存在,使得台风外围的扰动散度比扰动涡度的比值加大。
 | 图 6 扰动风差值矢量场与无摩擦的扰动高度(单位:m)场叠加图Fig. 6 Horizontal distributions of disturbed wind vector difference and disturbed height(m)without friction |
 | 图 7(a)扰动散度比值(有摩擦/无摩擦);(b)扰动散涡比比值(有摩擦/无摩擦)Fig. 7(a)Horizontal distributions of the ratio of divergence with friction to divergence without friction;(b)the ratio of divergence-vorticity ratio with friction to divergence-vorticity ratio without friction |
5 不考虑径向基本气流,只考虑水平扰动散度为零的情况
不考虑径向基本气流时,则在径向方向上满足梯度风平衡关系,且当考虑扰动散度为零的情况时,波动是沿着切向方向传播的涡旋Rossby波。具体讨论如下:
5.1 常微分方程组简化及数值差分方法
由方程(4)~(5)可以求得垂直扰动涡度方程:

其中,垂直扰动涡度 ,垂直平均涡度
,垂直平均涡度 ,水平扰动散度
,水平扰动散度 。
。
考虑正压水平无辐散的情况,假定水平扰动散度D'h为零,可以引进扰动流函数ψ',使得 ,代入到(13)之中,则得到如下的扰动流函数方程:
,代入到(13)之中,则得到如下的扰动流函数方程:

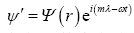 ,m、ω的含义同上,代入上式可得如下的常微分方程:
,m、ω的含义同上,代入上式可得如下的常微分方程:

依据实际情况,我们认为在台风中心跟台风最外围,台风波动很弱,即流函数的扰动振幅为零,因此给定内、外边界条件:

给出变量ψ在格点上的分布情况,即每个格点上均分布有变量ψ,编号为ψ1,ψ2,…ψk,ψ56,ψ57。具体分布情况如图 8。
 | 图 8 变量 的格点分布Fig. 8 Distribution of variable |
结合给定的边界条件,令ψ1=0,ψ57=0;从方程(15)中,我们可以明显地看到,在该微分方程中出现了三阶、四阶等高阶导数项,为了使中间位置格点上物理量的计算精度达到较高,并保证边 界处物理量的计算稳定性最好,我们对除边界外的各个格点上的三阶导数采用四点式差分方案,四阶导数采用五点式差分方案;而对于比较特殊 的、处于边界上的各阶导数计算的处理方案是,一阶导数 采用前、后插计 算,得到所有格点上的一阶导数值以后,采用同 样的方法,以一阶导数作为初始值,采用前、后插方法求解二阶导数的值,三阶、四阶的求解以此 类推。
采用前、后插计 算,得到所有格点上的一阶导数值以后,采用同 样的方法,以一阶导数作为初始值,采用前、后插方法求解二阶导数的值,三阶、四阶的求解以此 类推。
最后微分方程(15)式,离散化为:AX=ωBX,此时的A为55×55阶复数矩阵,B为55×55阶实数矩阵,ω为特征值,X为特征向量。同样的,通过对此矩阵求解,来研究分析当考虑粘性摩擦时,台风麦莎的波动结构会有什么变化。下面我们对计算结果进行分析。
5.2 粘性摩擦对波动结构特征和稳定性的影响
正压水平无辐散的条件下考虑粘性摩擦后,台风麦莎内部涡旋Rossby波的稳定性具有何种特征,我们给出此条件下的相角速度ωr/m和增长率ωi随波数的变化图表(其中波数m=1~10)。
在无摩擦情况下,涡旋Rossby波最不稳定的是2波(ωimax=2.441021),而波数在6~10的涡旋Rossby波是稳定不发展的;考虑粘性摩擦后,台风麦莎内部的涡旋Rossby波仍然表现为2波( )最不稳定,与无摩擦情况下的性质是一致的。比较相同波数下考虑摩擦和不考虑摩擦的波动增长率,可知受粘性摩擦影响后,同波数下的无摩擦的涡旋Rossby波的增长率比有摩擦情况下的要大,即受到粘性摩擦影响后涡旋Rossby波衰减,变得更加的稳定。考虑粘性摩擦后,涡旋Rossby波的波动相速度在半径r=200 km处在4.282~29.172 m/s之间。
)最不稳定,与无摩擦情况下的性质是一致的。比较相同波数下考虑摩擦和不考虑摩擦的波动增长率,可知受粘性摩擦影响后,同波数下的无摩擦的涡旋Rossby波的增长率比有摩擦情况下的要大,即受到粘性摩擦影响后涡旋Rossby波衰减,变得更加的稳定。考虑粘性摩擦后,涡旋Rossby波的波动相速度在半径r=200 km处在4.282~29.172 m/s之间。
| 表 1 涡旋Rossby波的相角速度ωr/m和增长率ωi随波数m(1~10)的变化 Table 1 The phase angular velocity(ωr/m) and growth rate(ωi)of the vortex Rossby waves as the function of wave number(1~10) |
同第一种情况,我们仍然用切向波数1为例来研究粘性摩擦对台风麦莎内部涡旋Rossby波波动结构的影响。图 9为台风麦莎内部的有摩擦对应的扰动流函数图。从扰动流函数量级的大小上看,涡旋Rossby波主要分布于距台风中心200 km以内的区域,这与重力惯性外波波动不同,重力惯性波主要分布在台风外围,说明台风Matsa内部不同性质波动的主要影响范围是不同的。考虑粘性摩擦后,扰动流函数的分布区域向台风中心收缩,即由原来的分布在距台风中心200 km范围内缩小为距台风中心100 km以内,在100 km到200 km之间,扰动流函数的强度明显减弱。
 | 图 9 有摩擦情况下扰动流函数(单位:m2/s)Fig. 9 Horizontal distributions of perturbed stream function(m2/s)with friction |
此外,我们由扰动流函数与扰动风矢量的转换公式得到扰动风矢量场(μ',ν'),再结合公式 ,求出扰动高度场h',下面我们给出有摩擦对应的扰动高度场与扰动风矢量场的叠加图(图 10)。
,求出扰动高度场h',下面我们给出有摩擦对应的扰动高度场与扰动风矢量场的叠加图(图 10)。
 | 图 10 有摩擦情况下扰动高度(单位:m)场与扰动风矢量(单位:m/s)场的叠加图Fig. 10 Horizontal distributions of perturbed height(m) and wind fields(m/s)with friction |
考虑摩擦力后的扰动高度场的大值区域比无摩擦情况下的区域沿径向向台风中心收缩,分布形态从无摩擦时的南北长东西短转变成为有摩擦时的南北短东西长,可以初步得出结论,无摩擦情况下在半径处于100~200 km范围内的原本扰动振幅较大区域在考虑摩擦存在的情况后,该区域内的扰动明显减弱。由上述得到的台风内部涡旋Rossby波的特征结构,结合模拟的雷达回波图(图 11),可以看出,在距台风中心200 km以内,同一半径圆周上台风的雷达回波呈现出2波的特征:台风中心的东、西(略偏北)两侧为雷达回波的大值中心,南、北方向对应雷达回波的小值中心。这与台风内部的涡旋Rossby波主要位于距台风中心200 km以内,且最不稳定(最显著)的Rossby波为2波的结论是一致的。
 | 图 11模拟的2005年8月6日15时雷达回波图 Fig. 11 The simulated radar echo at 1500 UTC 6 August 2005 |
从有摩擦对应的扰动涡度图(图 12)可见,对于1波而言,扰动涡度在同一圆周上呈反位相分布,扰动涡度的大值区域主要分布于距台风中心200 km以内,这与黄泓和张铭(2008)对热带气旋螺旋云带的动力不稳定的性质的研究是相似的,即在距离涡旋中心140 km范围以内,扰动相对涡度始终大于散度一个量级以上,而在140 km以外,涡度迅速衰减,散度量级超过涡度的量级。摩擦的存在使得扰动涡度的大值区域范围明显缩小,最大值的区域向台风中心靠拢至半径r<200 km以内,而不考虑摩擦时的扰动涡度大值区的分布范围明显比有摩擦情况大。
 | 图 12 有摩擦情况下扰动涡度图Fig. 12 Horizontal distributions of perturbed vorticity with friction |
为了更加清楚的呈现摩擦存在对涡旋 Rossby波的影响,接下来给出有摩擦减无摩擦的扰动风场差值矢量与原无摩擦的扰动高度场的叠加图和相应的扰动涡度场的比值图(图 13)。考虑摩擦后,在半径r<50 km内,扰动差值风场矢量场与扰动 高度场基本相平行,而在50 km<r<200 km范围内,差值风场矢量很小,且与扰动高度场明显不平行,说明涡旋Rossby波受摩擦影响后的确向着台风中心收缩。这些特点同样体现在扰动涡度的比 值图上。即在半径r<50 km内,扰动涡度比值为正,表明此范围内以涡旋运动增强,相反在25 km< r<200 km范围内,扰动涡度比值出现负值,涡旋运动作用明显减弱。综合以上表述,证明在摩擦的影响下,涡旋Rossby波波动范围向台风中心呈收缩的态势。
 | 图 13(a)扰动风差值矢量场与无摩擦的扰动高度(单位:10-6 m)场叠加图;(b)有摩擦与无摩擦的扰动涡度比值Fig. 13(a)Horizontal distributions of perturbed wind vector difference and perturbed height(10-6 m)without friction,and (b)the ratio of perturbed vorticity with friction to perturbed vorticity without friction |
考虑粘性摩擦后,台风内部的正压波动结构发生了显著的变化,上面两种情况是将重力惯性外波与涡旋Rossby波分开进行的研究和讨论。为了综合研究粘性摩擦对台风内部正压波动的影响,我们考虑包含所有波动的情况。
6.1 常微分方程简化与数值差分方法
考虑所有波动的情况,我们直接对(7)~(9)进行数值差分计算,不再对其进行简化。包含所有波动的情况,各变量的分布,格点的设计,导数项的差分表示方法以及边界上变量的处理等,都与分析重力惯性外波时所作的相关设置相一致,需要注意的是,该情况下唯一不同点是,所涉及的物理量 是根据梯度风平衡关系积分得到的,梯度风平衡关系式为
是根据梯度风平衡关系积分得到的,梯度风平衡关系式为 。
。
6.2 粘性摩擦对波动结构特征和稳定性的影响
研究稳定性(波动的增长率)的变化情况,我们同样给出m=1~200(不同波数)时相角速度ωr/m和增长率ωi的变化曲线图和无摩擦与有摩擦情况下的波动增长率的差值直方图(图 14a、b)。
 | 图 14(a)相角速度(单位:10-4 s-1ωr/m)和增长率ωi(单位:10-4 s-1)以及(b)波动增长率差值(无摩擦减去有摩擦)随波数的变化Fig. 14(a)The phase angular velocity(ωr/m) and growth rate(ωi) and (b)the difference between growth rates with and without friction as the function of wave number |
粘性摩擦对台风内部整体波动稳定性的影响效果与重力惯性外波对粘性摩擦的响应效果类 似,台风内部正压特征波动受到粘性摩擦的影响后,增长率为单峰值曲线,波数为45(ω45=1.18×10-3)左右表现为最不稳定;同样在增长率的差值(无摩擦的波动增长率减去有摩擦的波动增长率)直方图中,可以看到大部分差值为正值,即受到粘性摩擦影响后,台风内部正压波动衰减,特别指出m=1的波动衰减的最厉害,这与第一种考虑重力惯性波的情况是一致的。波数为1的波在半径r=1000 km(外螺旋雨带)波动的传播速度为 26.374 m/s;在半径r=200 km(内螺旋雨带),波速分别为 5.275 m/s。
给出m=1波时有摩擦所对应的扰动风场与扰动高度场的叠加图(图 15)。考虑摩擦力后,整体的矢量场与高度场扰动与无粘性摩擦情况下的表现一致,各扰动物理量场的分布表现出了重力惯 性外波的性质,整体波动的明显区域位于台风外围,风场以径向风扰动为主,扰动风矢量与扰动高度场基本相垂直。可见考虑粘性摩擦后,台风内部的正压特征波动仍然表现出重力惯性外波的性质特征。从给出的有摩擦对应的扰动散度场和扰动散涡比场(图 16)以及没有摩擦时的扰动散度场和扰动散涡比场(图略)可以看出,无论是否考虑粘性摩擦,散度扰动值均随半径的增加而增大,散涡比的绝对值大致均在1倍以上,甚至可以达到10倍,可见,对于所有波动而言,扰动运动以辐合辐散为主。
 | 图 15 有摩擦情况下扰动高度(单位:m)场与扰动风矢量(单位:m/s)场的叠加图Fig. 15 Horizontal distributions of perturbed height(m) and wind vector with friction |
 | 图 16 有摩擦情况下(a)扰动散度场和(b)扰动散涡比场Fig. 16 Horizontal disturbances of perturbed (a) divergence and (b) divergence–vorticity ratio with friction |
考虑到,单单从图 15、图 16中很难看出实际摩擦对风场和高度场波动所造成的影响,为此我们给出m=1波时的有摩擦与无摩擦的风场矢量差值图(图 17),如图所示,几乎在整个台风的范围内,风差值矢量与无摩擦时的风矢量的方向基本上是一致的。表明摩擦的存在使得扰动径向风分量加大,即边界层的摩擦使得径向风扰动加大。从有摩擦与无摩擦的扰动散度比值图(图 18a)可见,在整个台风范围内,有摩擦的散度与无摩擦散度的比值均为正值,表明摩擦的存在使得辐合辐散运动增强;而在扰动散涡比的比值图上,比值大致在+1以上,可见当摩擦存在后,台风内部的辐合辐散运动增强,扰动散度明显加大。
 | 图 17 扰动风差值矢量场与无摩擦的扰动高度(单位:m)场叠加图Fig. 17 Horizontal distributions of perturbed wind vector difference and perturbed height (m) without friction |
 | 图 18 (a)扰动散度比值(有摩擦/无摩擦)和(b)扰动散涡比比值(有摩擦/无摩擦)Fig. 18 (a) Horizontal distributions of the ratio of perturbed divergence with friction to perturbed divergence without friction and (b) the ratio of perturbed divergence-vorticity ratio with friction to perturbed divergence-vorticity ratio without friction |
考虑粘性摩擦后,台风边界层附近方位角平均下的径向风是不容忽视的,因此我们直接采用考虑径向基本气流的方程来研究台风波动结构受粘性摩擦的影响。具体分析如下:
7.1 常微分方程简化与数值差分方法
考虑径向基本气流后,我们直接对(7)~(9)进行数值差分计算。各变量的分布,格点的设计,导数项的差分表示方法以及边界上变量的处理等,都与分析重力惯性外波时所作的相关设置相一致。此时径向方向的动量方程的平均方程不再满足梯度风平衡,我们利用新的平衡关系式: ,积分求取
,积分求取 。
。
7.2 粘性摩擦对波动结构特征和稳定性的影响
从给出的相角速度ωr/m和增长率ωi的变化曲线图(图 19a)可见,增长率为单峰值曲线,最不稳定波波数在45左右,相角速度在m<10时,随波数的增加而减小,m>10时稳定少变。无摩擦与有摩擦情况下的波动增长率的差值大部分为正(图 19b),受到摩擦影响台风内部的波动确实是衰减了,这与前面得到的结论是一致的。波数为1的波在半径r=1000 km(外螺旋雨带)波动的传播速度为 30.324 m/s;在半径r=200 km(内螺旋雨带),波速分别为6.065 m/s。
 | 图19 (a)相角速度ωr/m(单位:10-4 s-1)和增长率ωi(单位:10-4 s-1)以及(b)波动增长率差值(无摩擦减去有摩擦)随波数的变化Fig. 19 (a) The phase angular velocity ( ωr/m ) and growth rate ( ωi) and (b) the difference between growth rates ωi with and without friction as the function of wave number |
考虑径向基本气流情况后,无论是否考虑摩擦,波数为1波的扰动高度场和扰动风场矢量场的结构特点均表现了重力惯性波的性质,从图 20中可以看出,波动大致区域位于台风的外围,扰动风场与高度场垂直。从给出的有摩擦的扰动散度场(图 21a)中可见,散度扰动均随半径的增加而增大,散涡比(图 21b)的绝对值在半径大于200 km以外,大致均在1倍以上,甚至可以达到10倍,可见,对于所有波动而言,扰动运动以辐合辐散为主。
为更加深入的理解考虑径向基本气流后摩擦存在对波动结构的影响,我们给出m=1波的有摩擦与无摩擦的风场矢量差值图(图 22a),如图所示,在600 km以内,考虑径向基本气流后的风差值矢量与无摩擦时的风矢量的扰动径向风的方向基本上是一致的,所得的结论与第6小节的结论是一致的。图 23a、c的扰动散度比值图和扰动散涡比的比值图,同样反映出扰动散度在大部分区域均是增大了。
 | 图 20 有摩擦情况下扰动高度(单位:m)场与扰动风矢量(单位:m/s)场的叠加图 Fig. 20 Horizontal distributions of perturbed height(m) and wind vector with friction |
 | 图 21 有摩擦情况下(a)扰动散度场和(b)扰动散涡比场Fig. 21 Horizontal distributions of perturbed(a)divergence and (b)divergence-vorticity ratio with friction |
径向基本气流的作用是不容忽视的,为研究在考虑粘性摩擦的情况下,径向基本气流的作用到底体现在哪里。我们给出了同样考虑粘性摩擦的情况下,有径向基本气流和无径向基本气流情况下的波动物理量的差值场。图 22b可以看出,在考虑径向基本气流后,风场扰动明显比不考虑径向基本气流的情况要强很多,反应在扰动散度比和扰动散涡比上,我们可以看出,扰动散度(图 23b)和扰动散涡比(图 23d)明显加大了,即与波动相联系的散度扰动场增强了。
 | 图 22 扰动风差值矢量场(a,考虑径向基本气流的有摩擦情况减去考虑径向风基本气流的无摩擦情况;b,考虑径向基本气流的有摩擦情况减去不考虑径向基本气流的有摩擦情况)与扰动高度(单位:m)场(a,考虑径向风基本气流的无摩擦扰动高度场;b,不考虑径向基本气流的有摩擦扰动高度场)叠加图 Fig. 22 Horizontal distributions of perturbed wind vector difference(a,between the situation with radial wind as well as friction and that with radial wind but without friction; b,between the situation with radial wind as well as friction and that without radial wind but with friction) and perturbed height(m)(a,without the friction but with the radial wind; b,without the radial wind but with the friction) |
 | 图 23(a,b)扰动散度比值和(c,d)扰动散涡比比值:(a,c)考虑径向风基本气流的有摩擦比无摩擦情况;(b,d)考虑径向基本气流的有摩擦情况比不考虑径向基本气流的有摩擦情况Fig. 23 Horizontal distributions of(a,b)the ratio of divergence and (c,d)the ratio of divergence-vorticity ratio:(a,c)That with friction and radial wind to that without friction but with radial wind;(b,d)that with friction and radial wind to that with friction but without radial wind |
本文从考虑地表摩擦的柱坐标系(r,l)下的正压大气运动方程组出发,分三种情况对台风麦莎个例进行了讨论分析,结果表明中尺度台风麦莎的正压特征波动结构及其稳定性均受到粘性摩擦的影响,但是就不同类型的波动其影响的效果是不同的。现将所得主要结论小结如下:
(1)为研究粘性摩擦对台风内部正压波动结构及其稳定性的影响,我们采用包含粘性摩擦在内的柱坐标系(r,l)正压大气运动方程组,并考虑到台风麦莎的实际情况,选取了麦莎登陆过程中大体位于陆地时的资料作为研究的出发场,所得的结论具有实际意义,与实际情况相符合;
(2)第一种情况下,重力惯性外波在台风外围最为明显,受摩擦的影响后,最不稳定波波数为45左右,增长率ωi曲线为单峰曲线,重力惯性波在摩擦的作用下衰减。波动的相速度为正值,波动沿着逆时针方向传播,波数为1的波速在r=1000 km处为47.43 m/s。在r>800 km范围外,径向风分量扰动明显增强,辐合辐散运动较无摩擦时增强;
(3)第二种情况下,涡旋Rossby波主要分布在台风中心附近,考虑粘性摩擦后,最不稳定的涡旋Rossby波为2波,涡旋Rossby波波动增长率减小,波速在半径r=200 km处的波速大小在4.282~29.172 m/s之间;考虑摩擦后,扰动高度场和扰动风矢量场的大值区域明显比无摩擦情况下的区域要小,即涡旋Rossby波的波动范围在摩擦的影响下,沿着径向向台风中心收缩,使得无摩擦时在半径处于100~200 km范围内的强扰动大大减弱,涡度在r<50 km内明显增强,涡旋Rossby波的波动区域明显减小;
(4)摩擦对包含所有波动情况的影响为:摩擦影响下的波动增长率呈单峰值曲线,波动在波数为45左右表现为最不稳定,此外波动在摩擦的影响下明显衰减,1波波速在r=1000 km处(外螺旋雨 带)大小为26.374 m/s;在半径r=200 km(内螺旋雨带)处的波速为5.275 m/s。摩擦的存在使得与波动相联系的径向风分量扰动明显加大,辐合辐散运动增强。
(5)考虑径向基本气流后,与扰动散度场相联系的扰动风矢量场有所增加,表明径向基本气流对散度有增强的作用,与波动有关的辐合辐散运动同样有所增大。波数为1的波在半径r=1000 km(外螺旋雨带)波动的传播速度为 30.324 m/s;在半径r=200 km(内螺旋雨带),波速分别为6.065 m/s。
本文对正压波动结构的研究具有一定的实际意义,但必须指出的是该正压模型具有一定的局限性,因为台风Matsa北上登陆进入斜压带,本身受到的斜压性的影响是不容忽视的。为此,考虑斜压结构、地形、热力等多种因素对台风结构的影响将是我们下一步的工作。
| [1] | Barat J. 1983. The fine structure of the stratospheric flow revealed by differential sounding[J]. J. Geophys. Res., 88: 5219-5228. |
| [2] | Chan K R, Scott S G, Bowen S W, et al. 1991. Horizontal wind fluctuations in the stratosphere during large-scale cyclogenesis[J]. J. Geophys. Res., 96: 17425-17432. |
| [3] | Chen D, Chen Z Y, Lü D R. 2011. Simulation of the stratospheric gravity waves generated by the typhoon Matsa in 2005[J]. Science China (Earth Sciences), 55: 602-610. |
| [4] | 丁一汇, 沈新勇. 1998. 非保守系统中的对称不稳定 I: 弱粘性的强迫作用[J]. 大气科学, 22: 145-155. Ding Y H, Shen X Y. 1998. Symmetric instability in nonconservative systems. Part I: Forcing effect of weak viscosity[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 22: 145-155. |
| [5] | Chen Y S, Yau M K. 2000. Spiral bands in a simulated hurricane. Part I: Vortex Rossby wave verification[J]. J. Atmos. Sci., 58: 2128-2145. |
| [6] | Eckermann S D, Voncent R A. 1993. VHF radar observations of gravity-wave production by cold fronts over southern Australia[J]. J. Atmos. Sci., 50: 785-806. |
| [7] | 黄泓, 张铭. 2003. 正压涡旋中螺旋波失稳问题的研究[J]. 热点气象学报, 19: 197-202. Huang H, Zang M. 2003. Study on destabilization of spiral wave in barotropic vortex[J]. Journal of Tropical Meteorology (in Chinese), 19: 197-202. |
| [8] | 黄泓, 张铭. 2008. 热带气旋螺旋云带动力不稳定的性质[J]. 气象学报, 66: 81-89. Huang H, Zhang M. 2008. Unstable dynamical properties of spiral bands in tropical cyclones[J]. Acta Meteor. Sinica (in Chinese), 66: 81-89. |
| [9] | 李崇银, 李桂龙. 1996. El Niño影响热带大气季节内振荡的动力学研究[J]. 大气科学, 20: 159-168. Li C Y, Li G L. 1996. A dynamical study of influence of El Niño on intraseasonal oscillation in tropical atmosphere[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 20: 159-168. |
| [10] | Li Y, Wang J Z, Chen L S, et al. 2007. Study on wavy distribution of rainfall associated with typhoon Matsa (2005)[J]. Chinese Science Bulletin, 52: 972-983. |
| [11] | Macdonald N J. 1968. The evidence for the existence of Rossby-like waves in the hurricane vortex[J]. Tellus, 20: 138-150. |
| [12] | Mark D P. 1989. Boundary layer structure and dynamics in outer hurricane rainbands. Part I: Mesoscale rainfall and kinematic structure[J]. Mon. Wea. Rev., 118: 891-917. |
| [13] | Michael T, Montgomery M T, Janice E. 1998. Tropical cyclogenesis via convectively forced vortex Rossby waves in a three-dimensional quasigeostrophic model[J]. J. Atmos. Sci., 55: 3176-3207. |
| [14] | Montgomery M T, Kallenbach R J. 1997. A theory for vortex Rossby-waves and its application to spiral bands and intensity changes in hurricanes[J]. Quart. J. Roy. Meteor. Soc., 123: 435-465. |
| [15] | Montgomery M T, Lu C. 1997. Free waves on barotropic vortices. Part I: Eigenmode structure[J]. J. Atmos. Sci., 54: 1868-1885. |
| [16] | Möller J D, Montgomery M T. 1999. Vortex Rossby waves and hurricane intensification in a barotropic model[J]. J. Atmos. Sci., 56: 1674-1687. |
| [17] | Möller J D, Montgomery M T. 2000. Tropical cyclone evolution via potential vorticity anomalies in a three-dimensional balance model[J]. J. Atmos. Sci., 57: 3366-3387. |
| [18] | Pierce R B, Fairlie T D A. 1993. Chaotic advection in the stratosphere: Implications for the dispersal of chemically perturbed air from the polar vortex[J]. J. Geophys. Res., 98: 18589-18595. |
| [19] | 沈新勇, 丁一汇. 1998. 对称扰动与纬向基流的相互作用II: 粘性波包的发展与弥散[J]. 大气科学, 22: 839-848. Shen X Y, Ding Y H. 1998. Interactions between symmetric disturbance and zonally basic flow. Part II: The development and dispersion of the viscosity wave packet[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 22: 839-848. |
| [20] | 沈新勇, 倪允琪, 张铭, 等. 2005a.β中尺度暴雨系统发生发展的一种可能物理机制I. 涡旋Rossby波的相速度[J]. 大气科学, 29: 727-733. Shen X Y, Ni Y Q, Zhang M, et al. 2005a. A possible mechanism of the genesis and development of meso-β rainstorm system. Part I. Phase velocity of vortex Rossby waves[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 29: 727-733. |
| [21] | 沈新勇, 倪允琪, 沈桐立, 等. 2005b.β中尺度暴雨系统发生发展的一种可能物理机制II. 涡旋Rossby波的形成[J]. 大气科学, 29: 854-863. Shen X Y, Ni Y Q, Shen T L, et al. 2005b. A possible mechanism of the genesis and development of meso-β rainstorm System. Part II. Formation of vortex Rossby waves[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 29: 854-863. |
| [22] | 沈新勇, 明杰, 方柯. 2007. 台风涡旋系统的波动性质及其数值模拟[J]. 气象科学, 27: 176-186. Shen X Y, Ming J, Fang K. 2007. The properties of wave in typhoon and its numerical simulation[J]. Scientia Meteorologica Sinica (in Chinese), 27: 176-186. |
| [23] | Stato K. 1989. An inertial gravity wave associated with a synoptic-scale pressure trough observed by MU radar[J]. J. Meteor. Soc. Japan, 67: 325-334. |
| [24] | Stato K. 1993. Small-scale wind disturbances observed by the MU radar during the passage of typhoon Kelly[J]. J. Atmos. Sci., 50: 518-537. |
| [25] | Sato K. 1994. A statistical study of the structure, saturation and sources of inertio-gravity waves in the lower stratosphere observed with MU radar[J]. J. Atmos. Terr. Phys., 56: 755-774. |
| [26] | Tanaka H, Yamanaka M D. 1984. Multiple ‘gust layers' observed in the middle stratosphere[C] // Holton J R, Matsuno T. Dynamics of the Middle Atmosphere: Proceedings of a Seminar held 8-12 November, 1982 in Honolulu, Hawaii. Tokyo, Japan: Terra Scientific Publishing Company, 117-140. |
| [27] | Tang X D, Tan Z M. 2006. Boundary-layer wind structure in a landfalling tropical cyclone[J]. Adv. Atmos. Sci., 23: 737-749. |
| [28] | Thomas L, Prichard I T, Astin I. 1992. Radar observations of an inertia-gravity wave in the troposphere and lower stratosphere[J]. Ann. Geophys., 10: 690-697. |
| [29] | Wang Y Q, Jeff D K, Greg J H. 2001. The effect of sea spray evaporation on tropical cyclone boundary layer structure and intensity[J]. Mon. Wea. Rev., 129: 2481-2500. |
| [30] | Willoughby H E. 1978a. A possible mechanism for the formation of hurricane rainbands[J]. J. Atmos. Sci., 35: 838-848. |
| [31] | Willoughby H E. 1978b. The vertical structure of hurricane rainbands and their interaction with the mean vortex[J]. J. Atmos. Sci., 35: 849-858. |
| [32] | Wu C C, Cheng H J, Wang Y Q, et al. 2009. A numerical investigation of the eyewall evolution in a landfalling typhoon[J]. Mon. Wea. Rev., 137: 21-40. |
| [33] | Xu Q. 1982. Unstable spiral inertia-gravity waves in typhoon[J]. Chinese Science (B), (7): 665-673. |
| [34] | 余志豪. 2002. 台风螺旋雨带—涡旋Rossby波[J]. 气象学报, 60: 502-507. Yu Z H. 2002. The spiral rain bands of cyclone and vortex Rossby waves[J]. Acta Meteor. Sinica (in Chinese), 60: 502-507. |
| [35] | 张立凤, 张铭. 1999. 斜压切变基流中横波型扰动的特征波动 I: 谱点分析[J]. 气象学报, 57: 571-580. Zhang L F, Zhang M. 1999. Characteristic wave of transversal disturbance at baroclinic shear flow. I: Spectrum analysis[J]. Acta Meteor. Sinica (in Chinese), 57: 571-580. |
 2013, Vol. 37
2013, Vol. 37

