2. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室, 北京100029
2. State Key Laboratory of Numerical for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
垂直湍流混合是海洋中最重要的物理现象之一,也是大洋环流模式需要解决的关键问题。在现有数值模式的分辨率条件下,解决湍流混合问题 只能依靠次网格参数化方案。在各种参数化方案中,垂直湍流混合系数(下文简称混合系数)的时空分布成为最关键也是最难解决的科学问题。长期以来,不同学者从理论和观测角度尝试解决这一难题。Munk and Wunsch(1998)和Munk(1966)从大洋中的平均垂直速度和维持温盐分布的大尺度平衡需要出发,推算出了全球大洋平均混合系数量级应为1 cm2 s−1。但是后来的研究尤其是观测事实表明(Gregg,1989;Ledwell et al.,1998;Osborn,1980),在大洋内部混合系数量级普遍为0.1 cm2 s−1,比大尺度平衡理论的结果小了一个量级。这说明垂直湍流混合强度在大洋中分布极不均匀,必然存在混合系数超过1 cm2 s−1的强混合区域。
由于现场直接观测混合系数技术困难、代价昂贵,一直以来只有极少量的直接观测数据,远不能满足大洋环流的研究需要。因此,许多学者发展了从其他较易观测到的物理量中推算出混合系数的方法。Osborn(1980)的经典工作使得从湍流动能耗散的观测数据中推算出混合系数成为可能,极大推动了实际大洋中垂直湍流混合的观测研究。St Laurent et al.(2012)、Nagasawa et al.(2007)、Thompson et al.(2007)等都采用Osborn(1980)的方法结合观测数据得出了大洋中特定区域混合系数的时空分布。
传统意义上认为湍流运动主要起能量耗散的作用,大量的数值模式仅从考虑海水运动的平均状态诱发湍流难易程度的角度来参数化湍流运动,而不考虑外部能量输入对湍流的影响。风和潮汐是大洋最主要的外部能量来源,在风能和潮汐能输入强的地区应当存在较强的垂直湍流,这个观点也已经被观测和理论研究所证实(Ledwell et al.,2000; Wang and Huang,2004a,2004b)。Craig and Banner(1994)由此从Mellor and Yamada(1982)的湍流混合理论出发,提出了从海洋表层风和波浪特征推算大洋中风浪引起湍流动能垂直耗散的参数化方案,下文简称CB94。CB94和Osborn方案相结合,可以建立由风、海浪估算海洋上层混合系数的一整套参数化方法。但是CB94方案并未考虑到海水密度的变化,因而也无法描述由密度变化而引起的重力位能改变,这在CB94方案所关注的海洋上层 100 m垂直范围内是近似合理的。
事实上,垂直湍流混合不仅会耗散能量、混合温盐,还可以通过改变大洋中的温盐层结进一步影响大洋中海水的重力位能(GPE:Gravitational Potential Energy)。一般情况下,由于大洋中以稳定层结为主,垂直混合会增加海水重力位能,因此大洋中的垂直混合不仅仅是动能能汇,也是重力位能能源(黄瑞新,1998)。在海洋中风浪较强的区域如南极绕极流(ACC:Antarctic Circumpolar Current),风浪可以影响到1000 m水深处的湍流混合,在这个深度上混合对重力位能的贡献有可能改变湍流动能耗散强度的垂直分布,从而进一步影响参数化的准确性。因此,本文将从能量平衡的角度出发,细致分析垂直混合对海水重力位能的影响,并进一步研究其对类似CB94的方案参数化100 m至风浪影响最大水深范围内混合系数的影响。
2 资料与计算方法 2.1 资料来源
本文使用了由美国国家海洋数据中心(NODC:National Oceanographic Data Center)提供的WOA09(World Ocean Atlas 2009)海洋温盐客观分析数据。该资料的覆盖范围为(89.5°S~89.5°N,0.5°E~0.5°W),水平分辨率为1°×1°,垂向0~5500 m分为33层,包含现场温度,实用盐度,溶解氧等数据,时间分辨率为气候态年平均和月平均。此外,还使用了由欧洲中期天气预报中心(ECMWF:The European Centre for Medium-Range Weather Forecasts)提供的ERA Interim(ECMWF Re- analyses Interim data)资料中的海表风应力和海表面波浪高度数据。数据空间分辨率为1.5°×1.5°,时间分辨率为6小时。
为满足本文研究需要,对原始数据做了预处理工作,将垂直上的不稳定层结通过垂直对流调整为稳定层结。本文用The Gibbs Sea Water(GSW)Oceanographic Toolbox of TEOS-10标准程序将WOA09中的现场温度转换成位温(以海平面为参考面),实用盐度转换为绝对盐度,并计算了每一层的现场密度和以海平面为参考面的位密σ0,用于进一步计算海洋上层的浮力频率。海洋中深层则用每一层深度为参考面计算上下相邻两层的位密,并进一步计算浮力频率。
2.2 计算方法本文的计算主要为混合系数引起的重力位能改变和风输入海洋上层的湍流动能耗散率及混合系数。
混合系数引起重力位能的改变计算流程如下:
(1)计算初始状态海水的重力位能,以WOA09中的海底最深处为参考面(5500 m)。
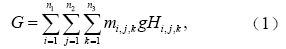
式中,i,j,k分别对应经向、纬向和垂直方向上的网格点编号,n1,n2,n3对应经向、纬向和垂直方向上的最大格点数。G为大洋海水总重力位能,mi,j,k为格点质量,g为重力加速度,本文取9.8 m s−1。Hi,j,k为格点质心和5500 m水深间的距离。
(2)计算混合后格点新的位温、盐度和现场密度。
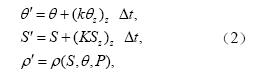
(3)计算混合后格点的新高度Hʹ和大洋新的重力位能Gʹ及重力位能改变△G。

(4)除了大洋总重力位能的变化,我们还需要详细了解每一层垂直混合对重力位能改变所做的贡献。实际计算中混合总是位于格点的界面上,因此每一界面的混合可细分为将下层格点的物质混合至上层及将上层格点物质混合致下层两个过程(图 1)。如果将这两个过程分开考虑,那么经混合后上、下两层格点新的位温应为
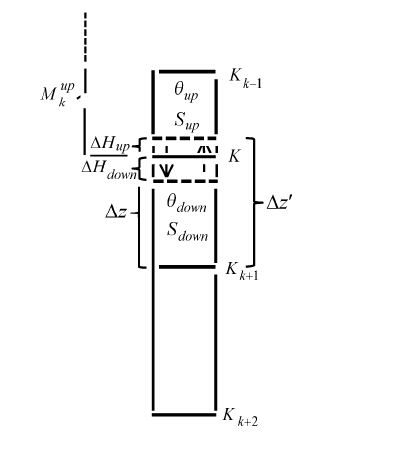 | 图 1 垂直混合对重力位能改变贡献的计算方法图示 Fig. 1 Diagram of calculation method for contribution of vertical mixing to GPE change |
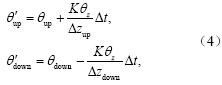
式中,下标up和down分别代表混合界面上、下格点的物理量,△z为格点厚度。类似的,我们也可导出上、下层相应的S'up、S'down、ρ'up、ρ'down以及相应的上、下层格点厚度因混合的变化△Hup、△Hdown。每一格点重力位能的贡献可以视作格点厚度的改变推动格点上方水柱上下位移而做的功。因此,每一层混合对整个大洋的重力位能贡献为Gi,j,kcon:
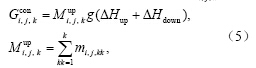
式中Mi,j,kup为格点上方水柱的总质量。理论上 如果计算过程精度足够高,那么应有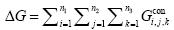 。实际计算过程中会发现,由于△H是非常小的量,再加上密度随海水温度、盐度和压力(温盐压)的非线性效应,计算结果会因计算精度不同而略有差异。
。实际计算过程中会发现,由于△H是非常小的量,再加上密度随海水温度、盐度和压力(温盐压)的非线性效应,计算结果会因计算精度不同而略有差异。
风输入海洋上层的湍流动能耗散率计算方案主要参照Baumert(2005)的方案,将海洋上层分为波浪混合层、湍流混合层和壁面律层(该层波浪混合效应按照普朗特湍流假设处理)分别计算(图 5a)。波浪混合层计算公式为
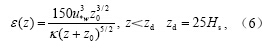
湍流混合层计算公式为
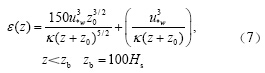
式中,ε(z)为不同水深的湍流动能耗散率,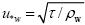 ;ι是海表面风应力;ρW是海水密度;z0按照Charnock(1955)和Soloviev and Lukas(2003)的估计约为au·w/g;a≈150000;Hs为海表面特征波高;κ为卡曼常数,本文取0.4;m为可调节的经验系数,参照Terray et al.(1996)、Kocsis et al.(1999)和Baumert(2005)的研究,本文取1.02;zd的取值参照Terray et al.(1996)的研究;zb的取值参照Kocsis et al.(1999)的研究。湍流混合层以下可以视为风浪无法影响到的区域,不进行参数化处理。由此只要确定τ和Hs,即可由公式(6)、(7)计算出局地风浪致湍流动能耗散率的垂直分布。
;ι是海表面风应力;ρW是海水密度;z0按照Charnock(1955)和Soloviev and Lukas(2003)的估计约为au·w/g;a≈150000;Hs为海表面特征波高;κ为卡曼常数,本文取0.4;m为可调节的经验系数,参照Terray et al.(1996)、Kocsis et al.(1999)和Baumert(2005)的研究,本文取1.02;zd的取值参照Terray et al.(1996)的研究;zb的取值参照Kocsis et al.(1999)的研究。湍流混合层以下可以视为风浪无法影响到的区域,不进行参数化处理。由此只要确定τ和Hs,即可由公式(6)、(7)计算出局地风浪致湍流动能耗散率的垂直分布。
本文首先计算了常混合系数下,全球大洋重力位能的变化,结果见图 2、图 3、图 4。从图 2中可看出,在常混合系数取0.1 cm2 s−1时,垂直混合引起的全球大洋重力位能分布非常不均匀,热带地区最高,北冰洋沿岸次之,南大洋地区最低。孟加拉湾、巴拿马湾、喀拉海和拉普捷夫海等有河流大量淡水注入的海域重力位能改变最显著。南中国海、东印度洋、赤道西太平洋等有大量热量输入的地区重力位能改变也较为显著。这种和温盐密切相关的空间分布形态说明了常混合系数下垂直湍流混合对重力位能的贡献受海洋层结的直接影响。全球平均的混合对重力位能贡献垂直分布也说明了这一点。在垂直分布图中,混合的贡献集中在水深200 m以 上,并在表层和约50 m处存在两个峰值。这与海洋上层层结性强是一致的,两个峰值则可能分别对应于海洋表层由于热量、淡水输入形成的强层结和季节性温跃层形成的强层结。
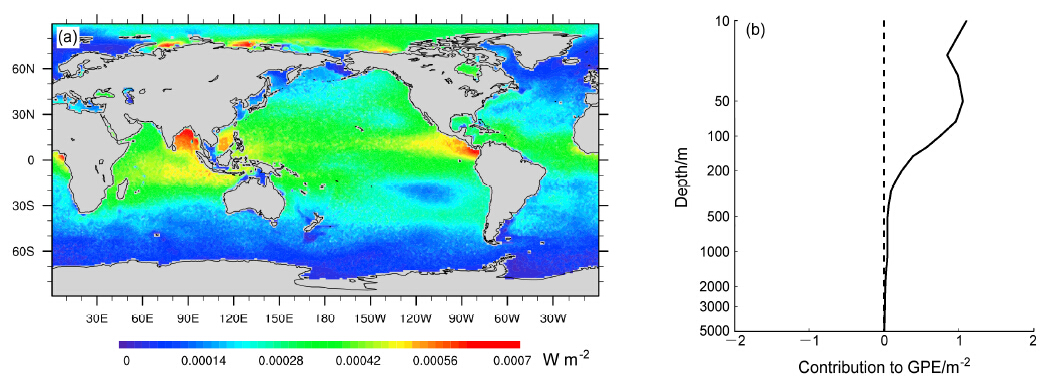 | 图 2 常混合系数(0.1 cm2 s−1)下(a)全球重力位能变化空间分布及(b)混合对重力位能贡献平均垂直分布 Fig. 2(a)Spatial distribution of global ocean GPE change and (b)vertical distribution of mean mixing contribution to GPE when mixing coefficient is 0.1 cm2 s−1 |
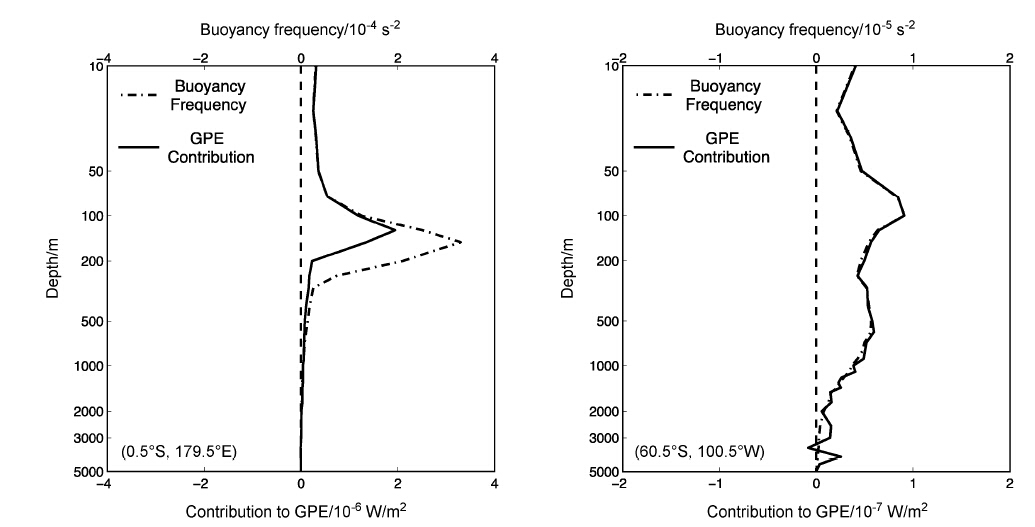 | 图 3 常混合系数(0.1 cm2 s−1)下低纬和高纬混合对重力位能贡献垂直分布示例 Fig. 3 Vertical distribution samples of mixing contribution to GPE at high latitude and low latitude when mixing coefficient is 0.1 cm2 s−1 |
 | 图 4 不同混合系数和浮力频率下重力位能变化:(a)不同常混合系数下全球大洋重力位能改变;(b)不同混合系数和浮力频率下的平均重力位能改变 Fig. 4 GPE change against mixing coefficients and buoyancy frequency:(a)Global GPE change vs. mixing coefficients;(b)mean GPE change vs. mixing coefficients and buoyancy frequency |
为进一步分析重力位能改变和层结的关系,本文分析了低纬和高纬两个样本浮力频率和混合致重力位能改变之间的关系(图 3)。低纬样本取自赤道西太平洋(0.5°S,179.5°E)处,高纬样本取自南大洋(60.5°S,100.5°W)处。从图 3中可以看 出,无论纬度高低,混合的贡献和浮力频率垂直分布形态都有非常好的吻合关系,在高纬二者几乎重合,低纬则略有出入。原因可能在于垂直混合并不是直接作用于密度,而是分别混合温盐进而影响密度,因此海水密度随温盐压的非线性变化会造成重力位能改变和代表密度层结的浮力频率不完全一致。
图 4给出了混合系数、浮力频率、重力位能三者之间的关系。由图 4a可以看出,混合系数和重力位能改变几乎呈线性关系,在0.1 cm2 s−1的常混合系数下,全球重力位能改变约为0.08 TW(1TW=1012 W),而在12 cm2 s−1的常混合系数下,重力位能改变可达12 TW。假定全球平均混合效率为0.2(Osborn,1980),则等效需要约60 TW的外部能量,这和Wang and Huang(2004a,2004b)的研究认为瞬时风变化能够输入海洋约60 TW能量的结论是一致的。密度随温盐压的非线性效应在这里虽然存在,但并不显著。这个计算结果和Urakawa and Hasumi(2009)的研究是一致的。由图 4b可知,层结趋于稳定和混合系数的增大都可以增加混合对重力位能的改变,三者之间主要呈正的线性关系,但也存在一定的非线性。结合前面的分析可得出,非线性关系主要存在于层结也即浮力频率和重力位能改变之间。
4 重力位能改变对风致湍流动能耗散参数化的影响由上文的分析可知,湍流混合能够引起大洋重力位能不可忽略的改变,尤其在混合系数为12 cm2 s−1时,对应所需的外部能量约为60 TW,这个量级已经十分接近风(Wang and Huang,2004a)和潮汐(Munk and Wunsch,1998)能够输入大洋的能量之和63.5 TW。如此大的能量必然会对大洋中的各种物理过程产生不可忽视的影响,不考虑这种影响的参数化方案可能同实际间存在较大的偏差。
Ledwell et al.(2011)通过DIMS(Diapycnal and Isopycnal Mixing Experiment in the Southern Ocean)试验得出了在南大洋东南太平洋海盆(62.5°S~55°S,110°W~95°W)处的混合系数和湍流动能耗散率2009年2月至2010年8月的平均垂直分布 [见Ledwell et al.(2011)图 1、图 3]。本文用ERA Interim相同区域和时间的风应力和波高数据,结合小节 1.2中的方法计算出相应的湍流动能耗散率,并进一步用Osborn(1980)的方案计算出混合系数以对比分析参数化的结果和实际观测间的差异。计算结果见图 5a。
 | 图 5 海洋上层修正前后的风浪致湍流动能耗散比较:(a)海洋上层风浪致湍流混合分层示意图;(b)修正前后的混合系数比较;(c)修正前后的湍流动能耗散率和湍流引起的重力位能改变比较 Fig. 5 The comparison of wind induced turbulent kinetic energy(TKE)dissipation before and after correction:(a)The upper ocean wind induced mixing layers diagram;(b)the comparison of mixing coefficient before and after correction;(c)the comparison of turbulent kinetic energy dissipation rate and GPE change before and after correction |
同Ledwell et al.(2011)的结果对比可以看出,参数化的湍流动能耗散率明显偏大,在水深100~400 m处偏大2个量级(图 5c),计算出的混合系数也明显偏大2个量级(图 5b)。本文认为这是没有考虑到垂直混合会增加重力位能的结果。如果考虑到由风浪输入表层的湍流动能在向下传播的过程中会不断转化为重力位能,那么参数化的结果应当扣除这部分能量才更合理。根据上文的分析,表层的混合对重力位能的贡献较小,因此可以假定表层垂直混合不影响混合系数。在此假定下可以计算从表层开始每一层参数化计算出的湍流动能耗散扣除该层以上转换为重力位能后的结果,从而可得修正后的湍流动能耗散,并进一步计算出该层混合系数。结果见图 5b、c。
由图 5b、c可知,修正后的湍流动能耗散比未经修正直接参数化的结果小2个量级,基本同Ledwell et al.(2011)的观测相同。但修正后的混合系数仍偏大一个量级,说明在湍流混合层中仍存在未知的能量耗散因素。由图 5c还可看出,垂直混合转化为重力位能在垂直方向上是一个累积的效应,虽然在风浪搅拌层混合转化为重力位能的量级远小于湍流动能耗散,但其累积效应到湍流混合层中已经可以显著影响到湍流耗散参数化。
5 结论本文利用WOA09资料,统计分析了不同混合系数下的大洋重力位能的变化,并探讨了其空间分布及可能原因。在此基础上,本文进一步讨论了垂直混合将湍流能量转化为重力位能后对湍流参数化的影响。主要的研究结论如下。
(1)垂直混合可以引起显著的大洋重力位能变化。仅0.1 cm2 s−1的混合系数就可引起约0.08 TW的重力位能改变,需要约0.4 TW的外部能量,实际大洋中外部能量远超这个数值,因此在气候态积分的海洋模式中,混合对重力位能的影响是不可忽视的。重力位能的改变程度同混合系数的大小和层结的强弱有关,一般来说由于海洋中以稳定层结为主,因此混合对重力位能的贡献以将外部能量转化为重力位能为主。混合系数越大,层结越强,垂直混合转化的重力位能越多。
(2)由于密度随温盐压变化是非线性的,混合增加的重力位能并不和密度层结线性相关,也不严格和混合系数大小线性相关。但从全球积分的角度可以认为混合系数和重力位能增加有近似线性关系:△G=0.94K-0.014。△G单位为TW,K单位为cm2 s−1。
(3)湍流混合参数化方案应当考虑湍流对外做功的效应。尤其在海洋次表层湍流参数化中,恰当考虑湍流转换为重力位能效应后(Baumert,2005)的方案可以得到和实际观测更接近的湍流动能耗散率,进一步计算出的混合系数也比修正前更接近实际观测。
在大洋中湍流不再仅仅是起耗散作用的能汇,而在一定程度上是能量通道,将外部能量转换至大洋重力位能。从能量的角度看,大洋中不仅存在传统意义上的障碍层——温跃层,也存在能量意义上的障碍层,也即混合转化重力位能极大区。在能量障碍层,湍流运动因需对外做功而受到抑制,从而进一步影响海洋中物质的湍流混合扩散。提供给混合的外部能量除了因转化为重力位能消耗外,还可能转换为其他形式,因此不仅风浪引起的湍流能量耗散参数化应当考虑不同能量间的转换,混合系数的参数化也应考虑这一点,这些都是值得深入研究的科学问题。此外,考虑能量转换的参数化方案在数值模式中的具体应用,也是未来值得深入研究的问题。
| [1] | Baumert H Z. 2005. A novel two-equation turbulence closure for high Reynolds numbers. Part B: Spatially non-uniform conditions [M].//Marine Turbulence: Theories, Observations, and Models. Cambridge:Cambridge Universith Press, 31-43. |
| [2] | Charnock H. 1955. Wind stress on a water surface [J]. Quart. J. Roy. Meteor.Soc., 81 (350): 639-640. |
| [3] | Craig P D, Banner M L. 1994. Modeling wave-enhanced turbulence in the ocean surface layer [J]. J. Phys. Oceanogr., 24 (12): 2546-2559. |
| [4] | Gregg M C. 1989. Scaling turbulent dissipation in the thermocline [J]. J.Geophys. Res., 94 (C7): 9686-9698. |
| [5] | 黄瑞新. 1998. 论大洋环流的能量平衡 [J]. 大气科学, 22 (4): 562-574.Huang Ruixin. 1998. On the balance of energy in the ocenic general circulation [J]. Scientia Atmospherica Sinica (in Chinese), 22 (4):562-574. |
| [6] | Kocsis O, Prandke H, Stips A, Simon A, et al. 1999. Comparison of dissipation of turbulent kinetic energy determined from shear and temperature microstructure [J]. J. Mar. Syst., 21 (1-4): 67-84. |
| [7] | Ledwell J R, Watson A J, Law C S. 1998. Mixing of a tracer in the pycnocline [J]. J. Geophys. Res., 103 (C10): 21499-21529. |
| [8] | Ledwell J R, Montgomery E T, Polzin K L, et al. 2000. Evidence for enhanced mixing over rough topography in the abyssal ocean [J]. Nature,403: 179-182. |
| [9] | Ledwell J R, St Laurent L C, Girton J B, et al. 2011. Diapycnal mixing in the antarctic circumpolar current [J]. J. Phys. Oceanogr., 41: 241-246. |
| [10] | Mellor G L, Yamada T. 1982. Development of a turbulence closure model for geophysical fluid problems [J]. Rev. Geophys., 20: 851-875. |
| [11] | Munk W, Wunsch C. 1998. Abyssal recipes II: Energetics of tidal and wind mixing [J]. Deep Sea Research Part I: Oceanographic Research Papers, 45:1977-2010. |
| [12] | Munk W H. 1966. Abyssal recipes [J]. Deep Sea Research and Oceanographic Abstracts, 13: 707-730. |
| [13] | Nagasawa M, Hibiya T, Yokota K, et al. 2007. Microstructure measurements in the mid-depth waters of the North Pacific [J]. Geophys. Res. Lett., 34:L05608. |
| Osborn T R. 1980. Estimates of the local rate of vertical diffusion from dissipation measurements [J]. J. Phys. Oceanogr., 10: 83-89. | |
| [14] | Soloviev A, Lukas R. 2003. Observation of wave-enhanced turbulence in the near-surface layer of the ocean during TOGA COARE [J]. Deep Sea Research Part I: Oceanographic Research Papers, 50: 371-395. |
| [15] | St Laurent L, Naveira Garabato A C, Ledwell J R, et al. 2012. Turbulence and diapycnal mixing in Drake Passage [J]. J. Phys. Oceanogr., 42:2143-2152. |
| [16] | Terray E A, Donelan M A, Agrawal Y C, et al. 1996. Estimates of kinetic energy dissipation under breaking waves [J]. Journal of Physical Oceanography, 26: 792-807. |
| [17] | Thompson A F, Gille S T, MacKinnon J A, et al. 2007. Spatial and temporal patterns of small-scale mixing in Drake Passage [J]. J. Phys. Oceanogr.,37: 572-592. |
| [18] | Urakawa L S, Hasumi H. 2009. The energetics of global thermohaline circulation and its wind enhancement [J]. J. Phys. Oceanogr., 39:1715-1728. |
| [19] | Wang W, Huang R X. 2004a. Wind energy input to the surface waves [J]. J.Phys. Oceanogr., 34: 1276-1280. |
| [20] | Wang W, Huang R X. 2004b. Wind energy input to the Ekman layer [J]. J.Phys. Oceanogr., 34: 1267-1275. |
 2014, Vol. 38
2014, Vol. 38


