2 北京师范大学全球变化与地球系统科学研究院, 北京100875;
3 中国科学院大学, 北京100049
2 College of Global Change and Earth System Science, Beijing Normal University, Beijing 100875;
3 University of Chinese Academy of Science, Beijing 100049
自从上世纪1960年代,Thompson(1957)和Lorenz(1963a,1963b)等人最早提出了确定性系统存在可预报性的问题,人们围绕该问题展开了大量的研究,对混沌系统的可预报性理论的认识逐渐深入。其中,研究误差的增长和传播规律问题成为可预报性理论的重要内容(穆穆等,2002;李建平等,2006;Li and Wang,2008)。一些工作先后从模型以及非线性动力学的角度来定量考察误差的增长。Thompson(1957)、Mintz(1964)、Leith(1965)等人先后尝试在模式内考察初始无限小误差随时间的倍增来衡量误差的增长速率,但是后来研究表明,这种做法相对依赖于数值模型本身(穆穆等,2002;Li et al.,2000;封国林等,2001;Gao et al.,2003)。Lorenz(1963b)提出在相空间里通过Lyapunov指 数 度量初始相邻相轨迹之间长期平均的指数发散率,表征初始无限小误差的增长率。经典Lyapunov指数虽然可以有效刻画系统的全局误差增长特征,但是在混沌吸引子内部,初始误差的发展并非处处相同(Legras and Ghil,1985;Nese,1989),有时我们更加关心相空间内局部的误差增长特征(李建平等,2006;丁瑞强和李建平,2007)。显然,经典Lyapunov指数理论在度量混沌吸引子局部误差的增长特征上具有一定的缺陷。
为了考察局部误差增长特征,Nese(1989)、Yoden and Nomura(1993)、Ziehmann et al.(2000)等提出了有限时间Lyapunov指数,用来衡量有限时间内初始误差的平均增长率。然而这些工作都是建立在线性理论框架的基础上,而随着误差的增长,系统会进入非线性阶段,切线性近似不再成立,因此需要发展非线性局部的误差增长理论(李建平等,2006;陈宝花等,2006)。李建平和丁瑞强等人提出了非线性局部Lyapunov指数(NLLE)(李建平等,2006;丁瑞强,2006;Ding and Li,2007;丁瑞强和李建平,2007;李建平和丁瑞强,2009;Li and Ding,2011),利用该指数,他们将局部动力演化相似方法(LDA)应用于观测资料,结合大气的动力学特征,分别研究了大气中不同变量场天气可预报性和气候可预报性的时空分布,天气可预报性的年代际变化,以及海温可预报性的时空分布等问题(Ding et al.,2008b;丁瑞强和李建平,2009a,2009b;Ding et al.,2010,2011;李建平和丁瑞强,2008;Li and Ding,2011,2013),这对于了解吸引子结构特征和度量混沌系统可预报性具有重要的意义。此外,NLLE方法还被用来研究初始状态的局部可预报期限问题(Ding et al.,2008a)。对于某固定初始状态的数值预报,其预报不确定性主要来源于初始分析误差和模式误差(Bergot et al.,1999;段晚锁等,2013)。在模式误差一定的条件下,为了减少初始分析误差对于预报质量的影响,目标观测是有效的手段之一。目标观测是一种改善数值预报质量的技术和方法,是在确定对预报结果具有潜在最大影响的区域基础上,通过移动观测手段增加观测,并结合同化方法减小数值模式中的初始分析误差,从而达到减小预报不确定性、延长预报时效的目的(Langland ,2005;Morss and Emanuel,2001;Zhou et al.,2012;Majumdar et al.,2011)。
目标观测的核心问题是如何确定敏感区的位置,敏感区是指初始分析误差较大或者增长很快或者对预报质量影响最大的区域(Langland ,2005)。传统上,研究目标观测问题的方法大多依赖于伴随模式(Buizza and Montani,1999;Bergot and Doerenbecher,2002;Baker and Daley,2000;Kim et al.,2004),导致实际应用中计算量巨大,同时这些方法多基于线性误差增长理论(Bishop and Toth,1999;Buizza and Montani,1999;Bergot and Doerenbecher,2002),而对于一些初始误差较大或者误差增长较快的个例来讲,线性近似是不成立的(穆穆等,2007)。为了克服线性假设的不足,穆穆等(Mu et al.,2006,2009)提出了条件非线性最优扰动(Conditional Nonlinear Optimal Perturbation,CNOP)方法研究天气和气候事件的可预报性,并成功将其应用于台风、ENSO等天气和气候事件的目标观测问题的研究(Riviere et al.,2008;Scheltinga and Dijkstra,2008;王斌和谭晓伟,2009;Tan et al.,2010;Wang and Tan,2010;Yu et al.,2012;Mu et al.,2014;Qin et al.,2013;Zhou and Mu,2011)。这些工作的提出对于目标观测问题的研究有着重要的理论与实际应用意义。此外,传统方法多依赖于数值模型,均假设模型是完美的(Buizza and Montani,1999;Bishop and Toth,1999;Bergot and Doerenbecher,2002),而模型误差是客观存在的,利用这些方法确定的敏感区不可避免的会受到模式误差的影响。因此用数值模式确定敏感区,须提前确定模式的模拟效果好,这是用数值模式确定敏感区的不方便之处,而NLLE可以直接用观测资料确定敏感区,避免了这一步。NLLE方法是研究误差非线性增长的重要理论,以往多被用于确定不同大小初始误差的可预报期限,其研究结果表明NLLE方法相对线性误差增长理论具有明显的优势(丁瑞强和李建平,2007; Li and Ding,2011),但是将该方法应用于研究目标观测问题的工作还未展开,所以验证NLLE方法能否被用来研究目标观测问题是开展该项工作的首要问题。
本文在前人工作的基础上,应用NLLE方法研究了单个初始状态局部平均的误差增长规律问题。首先,本文从理论上证明了在误差发展进入随机状态前,局部平均误差相对增长(LAGRE)与初始误差大小无关而是与初始状态有关;在误差演化进入随机状态后,LAGRE的饱和值由初始误差大小决定。并在Lorenz63模型(Lorenz,1963a)中验证了这一结论。其次,在局部动力演化相似方法(LDA)(丁瑞强和李建平,2009a;Li and Ding,2011)的基础上提出向前动力演化相似方法(FLDA)的概念,通过两个简单的混沌模型来说明LDA和FLDA方法能够有效的利用历史资料还原任意初始状态的误差增长率,为NLLE方法研究目标观测问题提供了依据,而在复杂模型中的验证将在下一步的工作中给出。 2 非线性局部Lyapunov指数方法
李建平和丁瑞强等(李建平等,2006;丁瑞强,2006;Ding and Li,2007;丁瑞强和李建平,2007;Li and Wang,2008;Li and Ding,2011)提出了NLLE理论和方法。对于一个n维非线性动力系统,对其误差演化方程不作任何近似,保留所有非线性项,误差演化方程的解可以从初始时刻t=t0到演化时刻t0+ε进行数值积分,得到
| $\delta ({t_0} + \varepsilon ) = \eta (x({t_0}),\delta ({t_0}),\varepsilon )\delta ({t_0}),$ | (1) |
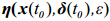 为非线性误差传播算子,
为非线性误差传播算子,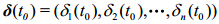 为初始误差向量。由(1)式定义非线性局部Lyapunov指数:
为初始误差向量。由(1)式定义非线性局部Lyapunov指数:
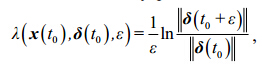
|
(2) |
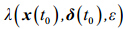 不仅依赖于相空间中参考轨道的初始状态x(t0)和演化时间ε,还与初始误差δ(t0)有关。为了方便,将向量δ(t0)的大小表示为||δ(t0)||。
不仅依赖于相空间中参考轨道的初始状态x(t0)和演化时间ε,还与初始误差δ(t0)有关。为了方便,将向量δ(t0)的大小表示为||δ(t0)||。
Li and Ding(2011)将NLLE方法应用于观测资料来定量研究系统的可预报性期限问题,提出了LDA方法确定单个变量的初始状态x(t0)在历史资料里的相似状态x(tk)。对于时间序列里所有的状态x(tj)((tj)和t0的间隔一定要足够长,这样可以避免持续性对相似点位置的影响),x(t0)和x(tj)之间的初始距离表示为
| ${d_i} = \left| {x({t_0}) - x({t_j})} \right|.$ | (3) |
| ${d_e} = \sqrt {\frac{1}{{K + 1}}{{\sum\limits_{i = 0}^K {\left[ {x({t_i}) - x({t_j} + i)} \right]} }^2}} ,$ | (4) |
为了讨论混沌系统里任意固定的初始状态 x(t0)的局部平均误差相对增长情况,在其周围施加一个小的初始误差域。该初始误差域可以被假想为相空间里以x(t0)为中心的一个圆球,圆球内部均匀分布着距离x(t0)大小不等、方向不同的初始误差(图 1)。
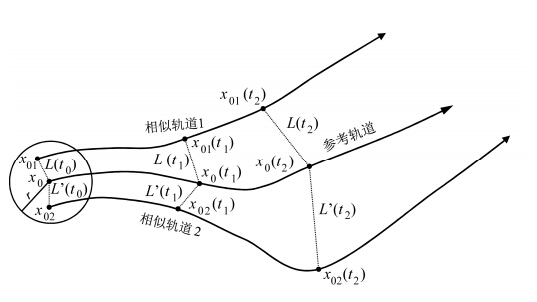 | 图 1 估计任意初始状态x0的LAGRE(局部平均误差相对增长)方法示意图。图中的圆球是以x0为中心、以初始误差域r为半径的球,x0(ti)是x0在第i时刻的演化,x01(ti)和x02(ti)分别是x0(ti)的相似状态,L(ti)和L'(ti)是相似状态和参考状态在第i时刻时的距离。计算参考轨迹和所有相似轨迹之间平均的NLLE,可以得到随时间变化的LAGRE Fig. 1 A schematic representation of the evolution procedure used to estimate the LAGRE(local average relative growth of initial error)of a r and om initial state from historical records. x0(ti)is the evolution state of x0 at the i-th time. x01(ti) and x02(ti)are the analogous states of x0(ti). L(ti) and L'(ti)denote the distance between the reference state and its analogues state at the i-th time. The average NLLE can be calculated between the reference trajectory and its all analogous trajectories to estimate the time-dependent LAGRE. |
定理(丁瑞强和李建平,2007;Ding and Li,2007):假设独立的随机变量X1,X2,…,Xn具有如下的概率分布:
| $f(x) = \left\{ \begin{array}{l} p(x),{\rm{ }}b \le x \le a,\\ 0,{\rm{ }}x < 或b{\rm{ }}{\rm{ }}x > a, \end{array} \right.$ | (5) |
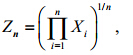
|
(6) |
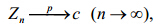
|
(7) |
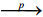 表示依概率收敛于,c为依赖于p(x)的一个常数。
表示依概率收敛于,c为依赖于p(x)的一个常数。
假设以初始状态x0为中心、以初始误差域r为半径的圆球内存在N条误差轨迹,计算参考轨迹和N条误差轨迹之间的NLLE,再对所有误差样本求平均,得到在误差演化进入随机状态之前只与初始状态有关的NLLE。数学表达式如下:
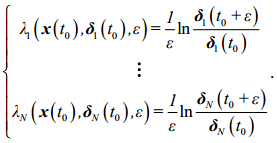
|
(8) |
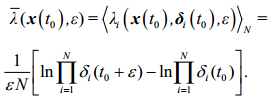
|
(9) |
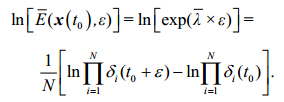
|
(10) |
由于受初始误差域的限制,样本足够多即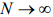 的情况下,δi(t0)将服从独立同分布,同理在t0+ε时刻,当
的情况下,δi(t0)将服从独立同分布,同理在t0+ε时刻,当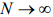 时,吸引子域的限制下,δi(t0+ε)也服从独立同分布。由定理可知,(10)式变为
时,吸引子域的限制下,δi(t0+ε)也服从独立同分布。由定理可知,(10)式变为
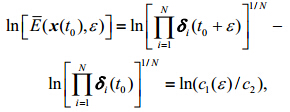
|
(11) |
在吸引子域和误差域的限制下,di(t0+e)的概率分布随e 变化,抽象到相空间内,吸引子域包含着初始误差域,初始误差域越小,则其达到覆盖吸引子域的时间越久,对应的可预报期限越长。反之,可预报期限越短。在误差演化时间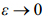 时,
时,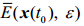 只与初始状态x(t0)和演化时间e 有关,当x(t0)和ε固定时,
只与初始状态x(t0)和演化时间e 有关,当x(t0)和ε固定时,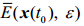 的值是固定的,对于一个固定的初始状态叠加不同大小的初始误差 域,c1和c2的比值不依赖于初始误差大小,也即LAGRE大小与初始误差无关的;而当误差演化进入随机状态后,初始误差域随时间逐渐增大最终覆盖整个吸引子域,此时c1值近似饱和代表整个吸引子域的大小,围绕一定值震荡。c1和c2的比值随着c1达到饱和而不再变化,近似为一个常数,且该常数依赖于初始误差大小,初始误差域越小则LAGRE的饱和值越大。在n维的混沌系统里,不同变量的可预报性不同。李建平和丁瑞强(2009)提出了单个变量的NLLE理论,能够有效的计算不同变量的可预报期限。不同变量的可预报性不一致,其本质是不同变量的误差增长快慢不同造成的。同样,对于某单个变量的初始状态施加一个小的误差域,在误差演化任意时刻,LAGRE仍依赖于c1和c2的比值,其证明过程和n维系统一致,这里从略。
的值是固定的,对于一个固定的初始状态叠加不同大小的初始误差 域,c1和c2的比值不依赖于初始误差大小,也即LAGRE大小与初始误差无关的;而当误差演化进入随机状态后,初始误差域随时间逐渐增大最终覆盖整个吸引子域,此时c1值近似饱和代表整个吸引子域的大小,围绕一定值震荡。c1和c2的比值随着c1达到饱和而不再变化,近似为一个常数,且该常数依赖于初始误差大小,初始误差域越小则LAGRE的饱和值越大。在n维的混沌系统里,不同变量的可预报性不同。李建平和丁瑞强(2009)提出了单个变量的NLLE理论,能够有效的计算不同变量的可预报期限。不同变量的可预报性不一致,其本质是不同变量的误差增长快慢不同造成的。同样,对于某单个变量的初始状态施加一个小的误差域,在误差演化任意时刻,LAGRE仍依赖于c1和c2的比值,其证明过程和n维系统一致,这里从略。
为了验证上述理论,利用Lorenz63模型(Lorenz,1963a)设计如下两个试验:(1)试验1,固定初始状态,分别改变叠加在该初始状态上的初始误差域的大小;(2)试验2,固定初始误差域,任选三个不同的初始状态。模型中的参数标准与文献(Lorenz,1963a)中相同,积分步长为0.01。试验1的结果如图 2所示,对于任意选取的一个初始状态,分别叠加不同大小的初始误差域,我们发现在误差演化进入随机状态之前,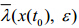 和
和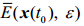 的对数是一致的,但是在误差演化进入随机状态后其值达到饱和,且饱和值大小不同,依赖于初始误差大小。在误差发展的线性阶段,LAGRE的大小显然只依赖于c1和c2的比值,与初始误差域大小无关。图 3是试验2的结果,描述了任意三个不同的初始状态在附加同一初始误差域时,
的对数是一致的,但是在误差演化进入随机状态后其值达到饱和,且饱和值大小不同,依赖于初始误差大小。在误差发展的线性阶段,LAGRE的大小显然只依赖于c1和c2的比值,与初始误差域大小无关。图 3是试验2的结果,描述了任意三个不同的初始状态在附加同一初始误差域时,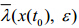 和
和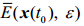 的对数随时间的演化,发现误差增长因为初始状态不同而存在着显著差异,但
的对数随时间的演化,发现误差增长因为初始状态不同而存在着显著差异,但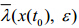 和
和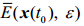 对数的饱和值相同,依赖于初始误差大小。综合试验1、2的结果,验证了在误差发展进入随机状态前,LAGRE大小只与初始状态有关,与初始误差域大小无关;在误差发展进入随机状态后,LAGRE的饱和值与初始误差大小有关这一结论。
对数的饱和值相同,依赖于初始误差大小。综合试验1、2的结果,验证了在误差发展进入随机状态前,LAGRE大小只与初始状态有关,与初始误差域大小无关;在误差发展进入随机状态后,LAGRE的饱和值与初始误差大小有关这一结论。
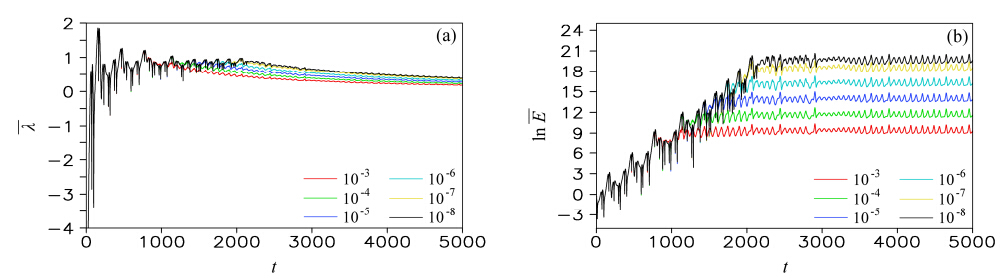 | 图 2 在Lorenz63系统里任选一个初始状态x01,不同初始误差域条件下,平均NLLE()以及局部平均误差相对增长()的自然对数随时间(无量纲)的变化。从上到下曲线对应的初始误差域分别为10−8、10−7、10−6、10−5、10−4、10−3 Fig. 2 For a certain initial state x01 in the Lorenz63 model,the mean NLLE() and the logarithm of LAGRE()against time steps(e)after adding different initial perturbation ensembles to the initial state. The curves from top to bottom are corresponding to the initial errors()of 10−8,10−7,10−6,10−5,10−4 and 10−3,respectively. |
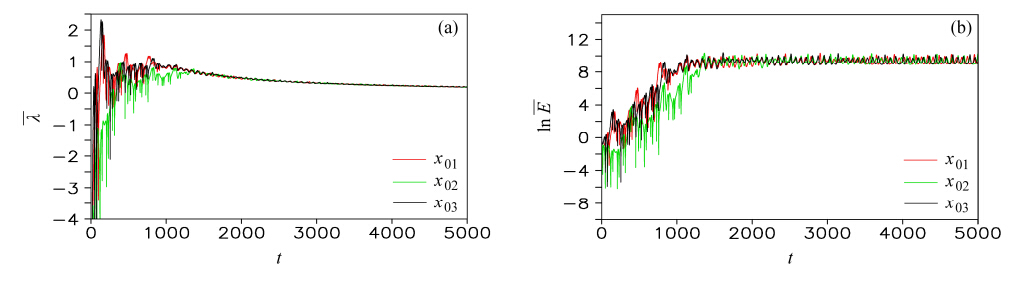 | 图 3 在Lorenz63系统里任选三个不同的初始状态x01、x02、x03,在相同的初始误差域条件下,平均NLLE()以及局部平均误差相对增长()的自然对数随时间(无量纲)的变化 Fig. 3 For three different certain initial states x01,x02,x03 in the Lorenz63 model,the mean NLLE() and the logarithm of LAGRE()against time steps(e)after adding the same initial perturbation ensembles to the initial state |
在n维相空间中,不同位置上的初始状态对于初始误差的敏感性存在差异,具体表现在对于相同大小的初始误差,不同初始状态的误差相对增长率是不同的,根据误差相对增长率的大小可以将相空间内存在的初始状态分为敏感的和非敏感的两类。对于敏感的初始状态,即使对其叠加的初始误差是无穷小的,其误差也能达到快速增长,而对于非敏感的初始状态,即使对其叠加较大的初始误差,其误差相对增长率仍然很小。Lorenz(1965)在利用28个变量的简单谱模式研究可预报期限随时间的变化时曾发现小扰动的增长在很大程度上依赖于参考轨迹在相空间中的位置,其本质上就是初始状态的敏感性存在差异而导致的。为了确定敏感状态在相空间中的位置,可以计算所有初始状态的LAGRE,大值对应着敏感的初始状态。
对于目标观测研究中所要寻找的敏感区,实际上就是初始场里分析误差增长较快的敏感初始状态所在的区域,所以只需计算出目标时刻LAGRE的空间分布,大值区即是敏感区。从前文可知,NLLE可以被有效的用于观测资料并计算出目标状态的LAGRE,但是其是否等于该目标状态理论上的LAGRE仍需要验证,而这是关系到NLLE方法能否被用于目标观测研究的关键问题,因此考虑使用两个简单的理论模型,Logistic(丁瑞强和李建平,2007)和Lorenz63进行验证。
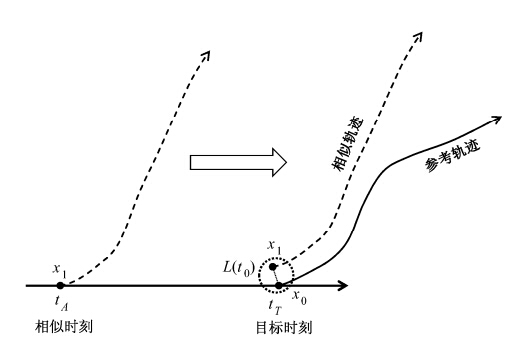 | 图 4 基于局部动力演化相似方法(LDA)计算目标时刻x0的LAGRE的方法示意图。x1是x0的相似状态,L(t0)是两个状态之间的距离。此种情形下,tT时刻之后的时间序列已知Fig. 4 A schematic representation for estimating the LAGRE by using LDA method. x1 is the analogues state of x0,and L(t0)is the distance between them. In this case,time series after tT is known. |
当NLLE方法被应用于观测资料研究目标观测问题时,根据目标状态之后的资料是否已知将问题分解为两类:一类是目标状态(tT)之后的时间序列已知时,可以应用局部动力演化相似方法去寻找目标状态(tT)的相似状态(tA),进而计算出目标时刻(tT)的LAGRE(图 4)。另一类则是目标状态(tT)之后的时间序列未知时,通过寻找目标时刻(tT)前的一小段序列(short interval)的相似轨迹,确定相似状态x'0的位置,计算tA时刻x'0的误差增长率代替目标时刻x0的LAGRE。对于前一种计算目标状态LAGRE的方法,我们称之为局部动力演化相似LDA方法,该方法要求混沌吸引子内部的两个相似状态之间,不仅初始距离要小,而且由这两个状态延伸出的相轨迹之间随时间的演化误差也要小。而对于后一种方法,由于在实际业务中,当前时刻之后的时间序列不可知,所以考虑寻找当前时刻之前一小段时间序列在历史资料里的相似轨迹,进而判定当前预报时刻的相似状态,并将其相似状态的LAGRE代替其自身的LAGRE,我们称这种方法为向前动力演化相似方法(FLDA)(图 5)。
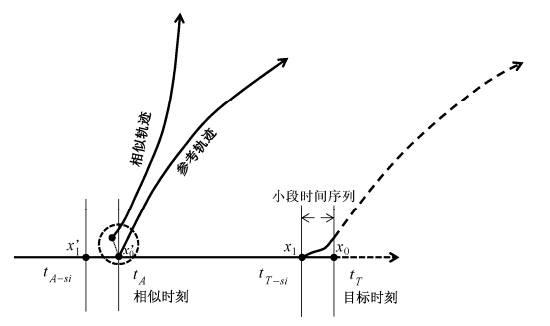 | 图 5 基于向前动力演化相似方法(FLDA)计算目标时刻tT时的LAGRE方法示意图。此种情形下,目标状态x0之后的时间序列未知,x1是tT之前一小段时间tT−si时刻的状态,通过局部动力演化相似方法确定x1在历史资料里tA−si时刻的相似状态x'1,进而确定x0在相似时刻tA时的相似状态x'0(tT和tT−si间隔很小),计算tA时刻的LAGRE代替tT时刻的LAGREFig. 5 A schematic representation for estimating the LAGRE by using FLDA method. In this case,time series after the target state x0 is not known. x1 is the state at the time of tT−si and its analogues state x'1 can be found through the LDA method,and the analogues state of x0 at the time of tA will be the state of x'0. The LAGRE of x0 can be replaced by that of x'0. |
下面分别通过Logistic和Lorenz63两个理论模型来验证LDA和FLDA利用观测资料计算所得到的LAGRE与理论值保持一致,结果分别见图 6、图 7。
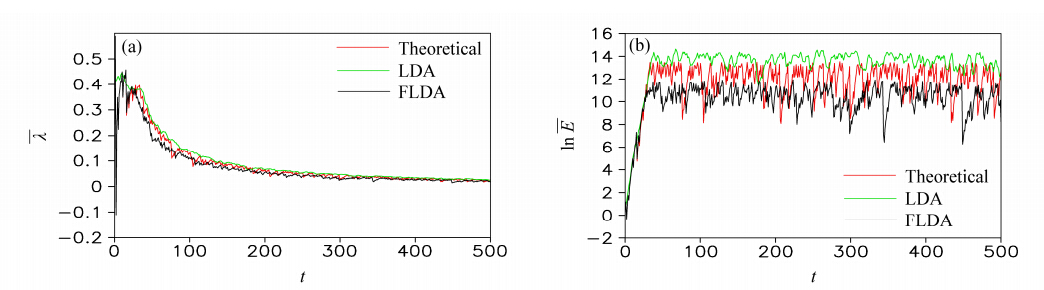 | 图 6 在Logistic系统里任选一个初始状态,平均NLLE 以及误差平均相对增长 的自然对数随t的变化。红色、蓝色和绿色曲线分别代表FLDA、LDA和理论的结果Fig. 6 For a certain initial state in the Logistic model,the mean NLLE() and the logarithm of LAGRE()against time steps(e). The black,green and red curves represent the LAGRE calculated by FLDA,LDA and theoretical growth,respectively |
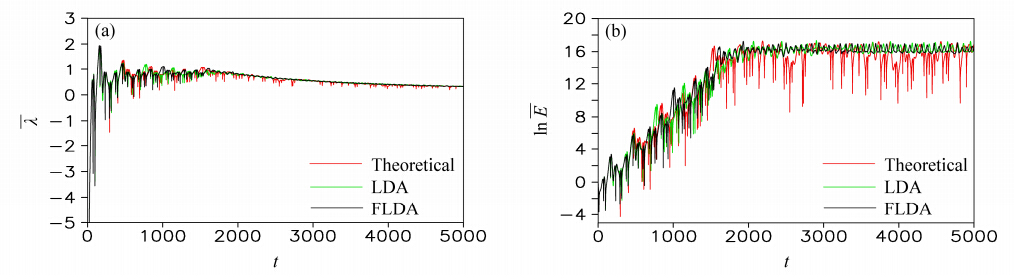 | 图 7 同图 6,但为Lorenz63模型中的结果Fig. 7 The same as in Fig. 6,but for the Lorenz63 model |
在Logistic模型里,积分步长为1,分别计算三种情况下对应的平均非线性局地Lyapunov指数(λ)和平均相对误差增长的对数(ln E)随时间的变化。比较LDA和FLDA的结果可以发现,用FLDA计算目标时刻的NLLE和LAGRE与用LDA算得目标时刻的NLLE和LAGRE在误差演化进入随机状态之前拟合较好,与初始误差大小无关,同时两者均和理论上的NLLE和LAGRE一致,说明LDA和FLDA方法能够有效的确定目标状态的NLLE和LAGRE,这使得在不借助模型的情况下,利用观测资料来研究目标观测问题成为可能。在Lorenz63模型里,积分步长为0.01,同样分别计算了三者对应的λ和ln E随时间的变化,得到了和Logistic模型里类似的结论。 5 总结和讨论
李建平和丁瑞强等人在线性误差增长理论的基础上,提出了NLLE方法(李建平等,2006;丁瑞强,2006;Ding and Li,2007;丁瑞强和李建平,2007;Li and Wang,2008;Li and Ding,2011),从整体上对非线性系统的动力特性进行研究,这对于可预报性问题的研究具有重要意义,但是对于局部误差增长特征并没有给出具体的研究。本文在其工作基础上,应用NLLE方法研究了单个初始状态局部平均的误差增长规律问题。首先,从理论上证明了在误差发展进入随机状态前,LAGRE只与初始状态有关;在演化进入随机状态后,LAGRE的饱和值与初始误差大小相关。并利用Lorenz63模型 验证了这一结论。其次,在LDA方法的基础上提出了FLDA的概念,通过两个混沌个例来说明 LDA和FLDA方法能够有效的利用历史资料还原任意初始状态的局部平均的误差相对增长率。
非线性误差增长规律对于研究目标观测具有重要的意义。应用NLLE方法容易得到误差增长率的空间分布,进而获得敏感区的空间分布。由于NLLE方法是基于观测资料的,所以回避了模型误差的影响。本文仅利用简单模型探讨了NLLE方法在目标观测中应用的可行性,未来将基于复杂模型以及实际观测资料考察NLLE方法研究目标观测问题的可行性与实际效果。
| [1] | Baker N L, Daley R.2000.Observation and background adjoint sensitivity in the adaptive observation-targeting problem[J].Quart.J.Roy.Meteor.Soc., 126 (565):1431-1454. |
| [2] | Bergot T, Doerenbecher A.2002.A study on the optimization of the deployment of targeted observations using adjoint-based methods[J].Quart.J.Roy.Meteor.Soc., 128 (583):1689-1712. |
| [3] | Bergot T, Hello G, Joly A, et al.1999.Adaptive observations:A feasibility study[J].Mon.Wea.Rev., 127 (5):743-765. |
| [4] | Bishop C, Toth Z.1999.Ensemble transformation and adaptive observations[J].J.Atmos.Sci., 56 (11):1748-1765. |
| [5] | Buizza R, Montani A.1999.Targeting observations using singular vectors[J].J.Atmos.Sci., 56 (17):2965-2985. |
| [6] | 陈宝花, 李建平, 丁瑞强.2006.非线性局部Lyapunov指数与大气可预报性研究[J].中国科学:地球科学, 36 (11):1068-1076.Chen Baohua, Li Jianping, Ding Ruiqiang.2006.Nonlinear local Lyapunov exponent and atmospheric predictability research[J].Science China:Earth Sciences (in Chinese), 36 (11):1068-1076. |
| [7] | 丁瑞强.2006.非线性误差增长理论与可预报性研究[D].中国科学院大气物理研究所博士学位论文.Ding Ruiqiang.2006.Nonlinear error dynamics and predictability study[D].Ph.D.dissertation (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Science. |
| [8] | 丁瑞强, 李建平.2007.误差非线性的增长理论及可预报性研究[J].大气科学, 31 (4):571-576.Ding Ruiqiang, Li Jianping.2007.Nonlinear error dynamics and predictability study[J].Chinese Journal of Atmospheric Sciences (in Chinese), 31 (4):571-576. |
| [9] | 丁瑞强, 李建平.2009a.非线性误差增长理论在大气可预报性中的应用[J].气象学报, 67 (2):241-249.Ding Ruiqiang, Li Jianping.2009a.Application of nonlinear error growth dynamics in studies of atmospheric predictability[J].Acta Meterologica Sinica (in Chinese), 67 (2):241-249. |
| [10] | 丁瑞强, 李建平.2009b.天气可预报性的时空分布[J].气象学报, 67 (3):343-354.Ding Ruiqiang, Li Jianping.2009b.The temporal-spatial distributions of weather predictability of different variables[J].Acta Meteorologica Sinica (in Chinese), 67 (3):343-354. |
| [11] | 段晚锁, 丁瑞强, 周菲凡.2013.数值天气预报和气候预测可预报性研究的若干动力学方法[J].气候与环境研究, 18 (4):524-538.Duan Wansuo, Ding Ruiqiang, Zhou Feifan.2013.Several dynamical methods used in predictability studies for numerical weather forecasts and climate prediction[J].Climatic and Environmental Research (in Chinese), 18 (4):524-538. |
| [12] | Ding R Q, Li J P.2007.Nonlinear finite-time Lyapunov exponent and predictability[J].Physics Letters A, 364 (5):396-400. |
| [13] | Ding R Q, Li J P, Ha K.2008a.Nonlinear local Lyapunov exponent and quantification of local predictability[J].Chin.Phys.Lett., 25 (5):1919- 1922. |
| [14] | Ding R Q, Li J P, Ha K.2008b.Trends and interdecadal changes of weather predictability during 1950s-1990s[J].J.Geophys.Res., 113, D24112, doi:10.1029/2008JD010404. |
| [15] | Ding R Q, Li J P, Seo K H.2010.Predictability of the Madden-Julian oscillation estimated using observational data[J].Mon.Wea.Rev., 138 (3):1004-1013. |
| [16] | Ding R Q, Li J P, Seo K H.2011.Estimate of the predictability of boreal summer and winter intraseasonal oscillations from observations[J].Mon.Wea.Rev., 139 (8):2421-2438. |
| [17] | 封国林, 戴新刚, 王爱慧, 等.2001.混沌系统中可预报性的研究[J].物理学报, 50 (4):606-611.Feng Guolin, Dai Xin'gang, Wang Aihui, et al.On numerical predictability in the chaos system[J].Acta Physica Sinica (in Chinese), 50 (4):606-611. |
| [18] | Gao X Q, Feng G L, Chou J F, et al.2003.On the predictability of chaotic systems with respect to maximally effective computation time[J].Acta Mechanica Sinica, 19 (2):134-139 |
| [19] | Kim H M, Morgan M C, Morss R E, et al.2004.Evolution of analysis error and adjoint-based sensitivities:Implications for adaptive observations[J].J.Atmos.Sci., 61 (7):795-812. |
| [20] | 李建平, 丁瑞强.2008.短期气候可预报期限的时空分布[J].大气科学, 32 (4):975-986.Li Jianping, Ding Ruiqiang.2008.Temporal-spatial distributions of predictability limit of short-term climate[J].Chinese Journal of Atmospheric Sciences (in Chinese), 32 (4), 975-986. |
| [21] | 李建平, 丁瑞强.2009.混沌系统单变量可预报性研究[J].大气科学, 33 (3):551-556.Li Jianping, Ding Ruiqiang.2009.Studies of predictability of single variable from multi-dimensional chaotic dynamical system[J].Chinese Journal of Atmospheric Sciences (in Chinese), 33 (3):551-556. |
| [22] | 李建平, 丁瑞强, 陈宝花.2006.大气可预报性研究的回顾与展望[C]// 21世纪初大气科学前沿与展望.北京:气象出版社, 96-104.Li Jianping, Ding Ruiqiang, Chen Baohua.2006.Review and Prospect on the predictability study of the atmosphere[C].Review and Prospects of the Developments of Atmosphere Sciences in Early 21st Century, Beijing:China Meteorology Press (in Chinese), 96-104. |
| [23] | Langland R H.2005.Issues in targeted observing[J].Quart.J.Roy.Meteor.Soc., 131 (613):3409-3425. |
| [24] | Leith C E.1965.Numerical simulation of the earth's atmosphere[M]// Methods in Computational Physics.New York:Academic Press. |
| [25] | Legras B, Ghil M.1985.Persistent anomalies blocking and variations in atmospheric predictability[J].J.Atmos.Sci., 42 (5):433-471. |
| [26] | Li J P, Wang S H.2008.Some mathematical and numerical issues in geophysical fluid dynamics and climate dynamics[J].Commun.Comput.Phys., 3 (4):759-793. |
| [27] | Li J P, Ding R Q.2011.Temporal-spatial distribution of atmospheric predictability limit by local dynamical analogues[J].Mon.Wea.Rev., 139 (10):3265-3283. |
| [28] | Li J P, Ding R Q.2013.Temporal-spatial distribution of the predictability limit of monthly sea surface temperature in the global oceans[J].Int.J.Climatol., 33 (8):1936-1947. |
| [29] | Li J P, Zeng Q C, Chou J F.2000.Computational uncertainty principle in nonlinear ordinary differential equations.I.Numerical results[J].Science in China (Series E), 43 (5):449-460. |
| [30] | Lorenz E N.1963a.Deterministic nonperiodic flow[J].J.Atmos.Sci., 20 (2):130-141. |
| [31] | Lorenz E N.1963b.The predictability of hydrodynamic flow[J].Trans.N.Y.Acad.Sci., Ser.II, 25 (4):409-433. |
| [32] | Lorenz E N.1965.A study of the predictability of a 28 variable atmospheric model[J].Tellus, 17 (3):321-333. |
| [33] | 穆穆, 李建平, 丑纪范, 等.2002.气候系统可预报性理论研究[J].气候与环境研究, 7 (2):227-235.Mu Mu, Li Jianping, Chou Jifan, et al.2002.Theoretical research on the predictability of climate system[J].Climatic and Environmental Research (in Chinese), 7 (2):227-235. |
| [34] | 穆穆, 王洪利, 周菲凡.2007.条件非线性最优扰动方法在适应性观测研究中的初步应用[J].大气科学, 31 (6):1102-1112.Mu Mu, Wang Hongli, Zhou Feifan.2007.A preliminary application of conditional nonlinear optimal perturbation to adaptive observation[J].Chinese Journal of Atmospheric Sciences (in Chinese), 31 (6):1102-1112. |
| [35] | Majumdar S J, Aberson S D, Bishop C H, et al.2011.Targeted observations for improving numerical weather prediction:An overview[R].Technical Report 15, World Weather Research Programme/THORPEX. |
| [36] | Mintz Y.1965.Very long-term global integration of the primitive equations of atmospheric motion[M].// WMO-IUGG Symposium on Research and Development Aspects of Long-Range Forecasting.WMO, Tech.Note, 66:141-155. |
| [37] | Morss R E, Emanuel K A.2001.Idealized adaptive observation strategies for improving numerical weather prediction[J].J.Atmos.Sci., 58 (2):210-232. |
| [38] | Mu M, Duan W, Xu H, et al.2006.Applications of conditional nonlinear optimal perturbation in predictability study and sensitivity analysis of weather and climate[J].Adv.Atmos.Sci., 23 (6):992-1002. |
| [39] | Mu M, Zhou F F, Wang H L.2009.A method to identify the sensitive areas in targeting for tropical cyclone prediction:Conditional nonlinear optimal perturbation[J].Mon.Wea.Rev., 137 (5):1623-1639. |
| [40] | Mu M, Yu Y S, Xu H, et al.2014.Similarities between optimal precursors for ENSO events and optimally growing initial errors in El Niño predictions[J].Theor.Appl.Climatol., 115 (3-4):461-469. |
| [41] | Nese J M.1989.Quantifying local predictability in phase space[J].Physica D, 35 (1-2):237-250. |
| [42] | Qin X H, Duan W S, Mu M.2013.Conditions under which CNOP sensitivity is valid for tropical cyclone adaptive observations[J].Quart.J.Roy.Meteor.Soc., 139 (675):1544-1554. |
| [43] | Riviere O, Lapeyre G, Talagrand O.2008.Nonlinear generalization of singular vectors:Behavior in a baroclinic unstable flow[J].J.Atmos.Sci., 65 (6):1896-1911. |
| [44] | Scheltinga van A D, Dijkstra H A.2008.Conditional nonlinear optimal perturbations of the double-gyre ocean circulation[J].Nonlinear Processes in Geophysics, 15 (5):727-734. |
| [45] | Tan X W, Wang B, Wang D L.2010.Impact of different guidances on sensitive areas of targeting observations based on the CNOP method[J].Acta Meteorologica Sinica, 24 (1):17-30. |
| [46] | Thompson P D.1957.Uncertainty of initial state as a factor in the predictability of large-scale atmospheric flow pattern[J].Tellus, 9 (3):275-295. |
| [47] | 王斌, 谭晓伟.2009.一种求解条件非线性最优扰动的快速算法及其在台风目标观测中的初步检验[J].气象学报, 67 (2):175-188.Wang Bin, Tan Xiaowei.2009.A fast algorithm for solving CNOP and associated target observation tests[J].Acta Meteorologica Sinica (in chinese), 67 (2):175-188. |
| [48] | Wang B, Tan X W.2010.Conditional nonlinear optimal perturbations:Adjoint-free calculation method and preliminary test[J].Mon.Wea.Rev., 138 (4):1043-1049. |
| [49] | Yoden S, Nomura M.1993.Finite-Lyapunov exponents stability analysis and its application to atmospheric predictability[J].J.Atmos.Sci., 50 (11):1531-1543. |
| [50] | Yu Y, Mu M, Duan W S, et al.2012.Contribution of the location and spatial pattern of initial error to uncertainties in El Niño predictions[J].J.Geophys.Res.:Oceans, 117, C06018, doi:10.1029/2011JC007758. |
| [51] | Zhou F F, Mu M.2011.The impact of verification area design on tropical cyclone targeted observations based on the CNOP method[J].Adv.Atmos.Sci., 28 (5):997-1010. |
| [52] | Zhou F F, Ding R Q, Feng G L, et al.2012.Progress in the study of nonlinear atmospheric dynamics and predictability of weather and climate in China (2007—2011)[J].Adv.Atmos.Sci., 29 (5):1048-1062. |
| [52] | Ziehmann C, Smith L A, Kurths J.2000.Localized Lyapunov exponents and the prediction of predictability[J].Physics Letters A, 271 (4):237-251. |
 2015, Vol. 39
2015, Vol. 39


