2 南京信息工程大学气象灾害教育部重点实验室, 南京 210044
2 Key Laboratory of Meteorological Disaster of Ministry of Education, Nanjing University of Information Science & Technology, Nanjing 210044
数值天气预报是一个初始场和边界条件的问题。准确的初始场在提高数值天气预报中起着重要作用,资料同化是为数值模式提供接近实际大气状态初始场的重要手段,其主要目的是通过适宜的算法将新的观测资料融入到模式场中,以得到更好的模式初值(Lewis et al., 2006)。经过数十年的发展,当前主流的同化方法分为变分同化法和集合同化法。前者主要包含三维变分(3DVAR)和四维变分(4DVAR)(Lewis et al., 2006);后者主要包含以集合卡尔曼滤波(EnKF)(Evensen, 1994,2003)为核心的,经过不同拓展延伸的集合同化方法,如集合变换卡尔曼滤波(ETKF)(Bishop et al., 2001; Livings,2005)、集合调整卡尔曼滤波(EAKF)(Anderson,2001)、集合均方根滤波(EnSRF)(Whitaker and Hamill, 2002; 邵长亮和闵锦忠,2015)以及很多其他改进算法如迭代集合平方根滤波(iEnSRF)(闵锦忠等,2012;王世璋等,2013)等。
尽管同化方法众多,但每一种同化思想都有各自的优缺点。EnKF方法由于采用了集合预报的思想,利用集合成员来计算背景误差协方差矩阵(P矩阵),实现了背景误差协方差的流依赖,同时避免了4DVAR同化中对切线性模式和伴随模式的构建。这使得EnKF相比3DVAR、4DVAR更加适合应用到发展较快、变化迅速的中小尺度过程中(Yang et al., 2009)。然而,为了构造具有代表性的P矩阵需要大量的集合成员,增大了模式的计算量;而较小的集合成员容易产生滤波发散。同时,EnKF方法的局地化操作以及在同化过程中造成的不连续性所带来的高频振荡可能会破坏模式变量的平衡关系(Bloom et al., 1996; Ourmières et al., 2006; Kepert,2009)并造成数据损失,从而引入误差。这些缺点在对初值敏感的中小尺度过程中 都是极为不利的。
张驰逼近(Nudging)(Hoke and Anthes, 1976)是一种传统的连续同化方法,通过对模式积分方程添加Nudging项使每一步积分都能向观测场逼近,并且积分时间越长同化效果越好(Lakshmivarahan and Lewis, 2013)。Nudging方法作用于每一积分步,其同化过程不会造成严重的不连续问题;由于利用了模式积分进行动力约束,不会破坏模式各变量间的物理平衡;但存在同化收敛较慢、资料利用不够充分的问题。为了克服这一缺点,Auroux and Blum(2005,2008)提出了Back and Forth Nudging(BFN)方法:通过向前、向后积分迭代增加积分时间,以加快Nudging同化收敛速度,实现对观测资料的充分利用。通过与中尺度气象业务预报模式Meso-NH model(Boilley and Mahfouf, 2012)和海洋业务预报模式NEMO(Ruggiero et al., 2015)对接,试验证明BFN方法有与4DVAR相当的同化效果。
为了解决EnKF的同化不连续问题,Lei et al.(2012a,2012b)提出了Hybrid Nudging EnKF(HNEnKF)方法,其基本思想是使用EnKF的卡尔曼增益矩阵K作为Nudging算子引入模式预报方程,最后将Nudging同化的结果与利用EnKF更新后的集合扰动相加,得到新的集合成员。Lei et al.(2012a,2012b)在文章中用Lorenz 63模式和浅水模式进行了试验,取得了较好的效果:在Lorenz63模式中,HNEnKF方法的连续性好于传统EnKF方法和分析增量法(IAU)(Bloom et al., 1996; Ourmières et al., 2006),并与集合卡尔曼平滑(EnKS)(Evensen and van Leeuwen,2000)相当;在浅水模式下,HNEnKF的同化效果优于EnKF和EnKS。然而当同化窗口增大时,HNEnKF方法 的同化效果明显降低;模式均方根误差(RMSE)收敛速度依然较慢;如本文前述,Nudging算法 的特性在于积分时间越长,同化效果越好(Lakshmivarahan and Lewis, 2013),简单地将Nudging算子用卡尔曼增益矩阵进行替换的混合方法,并不能充分发挥其同化效果。
为解决上述问题,本文根据HNEnKF方法的混合思路,将BFN算法与EnKF进行结合,设计了新的混合算法:Hybrid Back and Forth Nudging EnKF(HBFNEnKF)同化方法,并用浅水模式(shallow water model)进行了几组同化试验,详细讨论了结果。新算法采用了BFN前后积分迭代的思路,使同化过程能很快收敛,同时能对非观测模式变量进行较好调整;此外,HBFNEnKF保留了HNEnKF良好的同化连续性;在模式方程约束下,其各变量间的平衡关系得到维持。对HNEnKF和HBFNEnKF方法的介绍将在文章第二部分给出,第三部分的内容是试验方案设计,试验结果与分析在第四部分给出,第五部分为全文总结。
2 基本同化算法介绍 2.1 EnSRF同化方法EnSRF是EnKF同化方法的一个重要分支,本文设计的HBFNEnKF方法也采用了EnSRF的思路计算卡尔曼增益矩阵、更新集合扰动。传统的EnKF为了避免对背景误差协方差的低估,采用了在观测资料中添加随机扰动的方法,这样一来会在同化中引入扰动误差(Whitaker and Hamill, 2002)。EnSRF方案则通过一系列的变换,避免了这一误差。
EnSRF的同化过程分为两步:
| $X_{i}^{b}(t)=M\left( X_{i}^{a}(t-\text{1}) \right)$ | (1) |
| $\overline{{{\mathbf{X}}^{a}}}=\overline{{{\mathbf{X}}^{b}}}+\mathbf{K}({{\mathbf{y}}^{o}}-\overline{\mathbf{H}{{\mathbf{X}}^{b}}})$ | (2) |
| $\mathbf{{X}'}_{i}^{a}=\mathbf{{X}'}_{i}^{b}-\alpha \mathbf{KH{X}'}_{i}^{b}$ | (3) |
其中,(1)式为预报步,M代表模式预报方程,X代表模式预报变量,上标a代表同化后的分析值,上标b代表预报值或背景场,下标i代表第i个集合成员。(2)、(3)式为分析步,(2)式用于更新集合平均,(3)式用于更新集合扰动,H为观测算子,
| $\mathbf{K}={{\mathbf{P}}^{b}}{{\mathbf{H}}^{T}}{{(\mathbf{H}{{\mathbf{P}}^{b}}{{\mathbf{H}}^{T}}+\mathbf{R})}^{-1}}$ | (4) |
| ${{\mathbf{P}}^{b}}{{\mathbf{H}}^{T}}\approx [(\mathbf{X}_{i}^{b}-\overline{{{\mathbf{X}}^{b}}}){{(\mathbf{HX}_{i}^{b}-\overline{\mathbf{H}{{\mathbf{X}}^{b}}})}^{T}}]$ | (5) |
| $\mathbf{H}{{\mathbf{P}}^{b}}{{\mathbf{H}}^{T}}\approx [(\mathbf{HX}_{i}^{b}-\overline{\mathbf{H}{{\mathbf{X}}^{b}}}){{(\mathbf{HX}_{i}^{b}-\overline{\mathbf{H}{{\mathbf{X}}^{b}}})}^{\operatorname{T}}}]$ | (6) |
其中,
| $\alpha ={{\left[ 1+\sqrt{\mathbf{R}{{(\mathbf{H}{{\mathbf{P}}^{b}}{{\mathbf{H}}^{T}}+\mathbf{R})}^{-1}}} \right]}^{-1}}$ | (7) |
由于α的引入,EnSRF方法能得到与EnKF一致的分析误差协方差矩阵,同时避免了因对观测场添加随机扰动带来的扰动误差。
2.2 Nudging同化方法和BFN同化方法介绍Nudging同化也被称为牛顿张驰逼近法,是一种连续同化方法,通过在预报方程加入Nudging项使得模式变量在积分过程中逐步逼近真值。传统的Nudging同化公式为
| $\frac{d\mathbf{X}}{dt}=F(\mathbf{X})+{{t}_{{{w}_{t}}}}\cdot \mathbf{G}\cdot ({{\mathbf{y}}^{o}}-\mathbf{HX})$ | (8) |
式中,F(X)为模式预报方程,
| ${{t}_{{{w}_{t}}}}=\frac{{{w}_{t}}}{\left( \sum\limits_{t={{t}_{o}}-{{t}_{N}}}^{{{t}_{o}}}{{{w}_{t}}\cdot \Delta t} \right)}\ \text{ },$ | (9) |
其中,
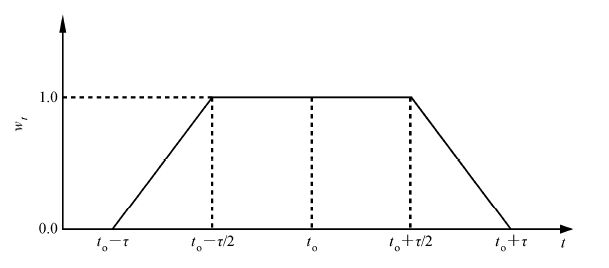
| ${{w}_{t}}=\left\{ \begin{align} & 1\text{ , }\left| t-{{t}_{o}} \right|<{\tau }/{2\text{,}}\; \\ & \frac{(\tau -\left| t-{{t}_{o}} \right|)}{{\tau }/{2}\;},\text{ }{\tau }/{2}\;\le \left| t-{{t}_{o}} \right|\le \tau \text{,} \\ & 0,\text{ }\left| t-{{t}_{o}} \right|>\tau \text{,} \\ \end{align} \right.$ | (10) |
式中,
|
图 1 权重系数wt随时间变化的示意图 Figure 1 Temporal weighting function wt in the time window |
理论上,采用Nudging同化会使模式场随着积分不断收敛于真值(Lakshmivarahan and Lewis, 2013),但要求Nudging算子G既不能太大,导致积分不稳定,也不能太小,使得收敛速度太慢,降低同化效果。在通常的业务模式如WRF模式中,G的取法为Cressman反距离权重法(Stauffer and Seaman, 1990; Liu et al., 2005,2006),Stauffer and Seaman(1990),Stauffer and Bao(1993)以及Zou et al.(1992)提出了最优逼近(Optimal Nudging),利用伴随矩阵求解对应的代价函数,得出某一同化区间的最优Nudging算子。然而这样的求解方式需要伴随模式的构建,加大了操作难度。
从增加模式积分时间的角度考虑,Auroux and Blum(2005,2008)提出了BFN方法,其基本思路为
| $\left\{ \begin{align} & \frac{d{{\mathbf{X}}_{k}}}{dt}=F\left( {{\mathbf{X}}_{k}} \right)+{{t}_{{{w}_{t}}}}\cdot \mathbf{G}({{\mathbf{y}}^{o}}-\mathbf{H}{{\mathbf{X}}_{k}}), \\ & {{\mathbf{X}}_{k}}\left( 0 \right)={{{\mathbf{\tilde{X}}}}_{k-1}}\left( 0 \right), \\ \end{align} \right.$ | (11) |
| $\left\{ \begin{align} & \frac{d{{{\mathbf{\tilde{X}}}}_{k}}}{dt}=F\left( {{{\mathbf{\tilde{X}}}}_{k}} \right)-{{t}_{{{w}_{t}}}}\cdot \mathbf{{G}'}\left( {{\mathbf{y}}^{o}}-\mathbf{H}{{{\mathbf{\tilde{X}}}}_{k}} \right), \\ & {{{\mathbf{\tilde{X}}}}_{k}}\left( T \right)={{\mathbf{X}}_{k}}\left( T \right). \\ \end{align} \right.$ | (12) |
(11) 式为向前逼近(Forward Nudging),(12)式为向后逼近(Backward Nudging)。其中,
| $\mathbf{G}(\mathbf{G}')=\mu {{\mathbf{H}}^{T}}{{\mathbf{R}}^{-1}}$ | (13) |
其中,μ为常数。
BFN同化方法的步骤为:利用Forward Nudging将模式向前积分到同化窗口终点,将模拟结果赋给Backward Nudging作初值;利用Backward Nudging将模式向后积分到窗口起始时刻,把模拟结果赋给Forward Nudging,由此不断迭代直至收敛。由于模式的非线性特性,向后积分会产生较强的不稳定,但在Backward Nudging里,Nudging项的引入使向后积分得以较为稳定地进行,由此构建出不需要伴随模式的四维同化方案。
Auroux and Blum(2005,2008)证明了BFN同化方法的收敛性和较好的同化效果,但实际上该方法也存在很多问题:(1) Auroux and Blum(2005,2008)给出的Nudging算子仅是一个近似,并未给出明确的标准,对的取值较为随意;(2) 观测误差协方差矩阵在实际中有时无法确定,而计算切线性观测算子需要复杂的操作;(3) 为了达到好的同化效果,BFN同化需要较多次迭代才能收敛(Auroux,2009),使同化花费了很多时间。
2.3 混合方法介绍为了解决EnKF的同化不连续问题,Lei et al.(2012a,2012b)提出了HNEnKF同化方案,该方法中Nudging算子的替换公式为
| ${{t}_{{{w}_{t}}}}\cdot \mathbf{G}=\frac{{{w}_{t}}}{\left( \sum\limits_{t={{t}_{o}}-{{\tau }_{\operatorname{N}}}}^{{{t}_{o}}}{{{w}_{t}}\cdot \Delta t} \right)}\cdot \mathbf{K}$ | (14) |
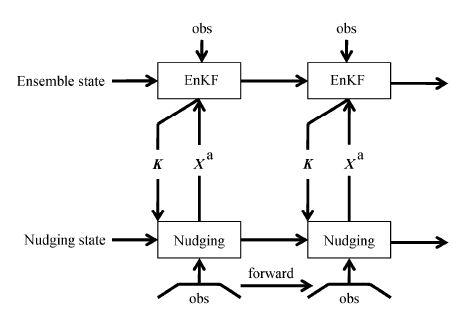
HNEnKF的同化步骤为:首先将集合成员积分到同化时次,利用(4)式计算得到K,然后按照(14)式的混合方案计算出Nudging对应的同化算子,将模式积分到同化时刻;用Nudging积分后的结果替换掉集合平均场,与EnKF更新后的集合扰动相加,得到新的集合成员;将集合成员继续向前积分,循环同化。HNEnKF与IAU有很多相似之处,但其最大不同在于:IAU在积分步上叠加的增量是静态的,HNEnKF同化则使用随时间变化的分析增量进行叠加。图 2给出了HNEnKF方法的详细同化流程。
|
图 2 HNEnKF方案的同化流程示意图 Figure 2 Procedures of the HNEnKF (Hybrid Nudging Ensemble Kalman Filter) scheme |
如前所述,HNEnKF方法还存在一些问题。为了改进该方法,本文结合Auroux and Blum(2005,2008)提出的BFN算法与EnKF,设计了HBFNEnKF混合方法。其原理为:将(11)、(12)式中的G、利用下式进行替换:
| $\mathbf{G}(\mathbf{G}')=\beta \cdot \mathbf{K}$ | (15) |
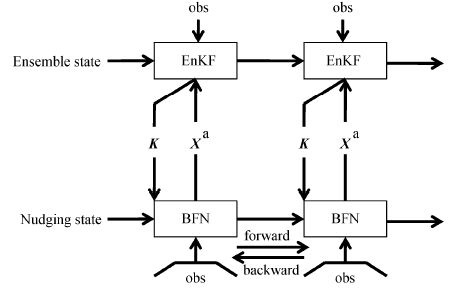
为了使得向前向后积分更加稳定,引入参数进行控制。HBFNEnKF的步骤与HNEnKF的主要区别是:将HNEnKF中只进行单向积分的Nudging同化改为使用(15)式计算得到
|
图 3 HBFNEnKF方案的同化流程示意图 Figure 3 Procedures of the HBFNEnKF (Hybrid Back and Forth Nudging EnKF) scheme |
为了检验HBFNEnKF的同化效果,本文首先在通道浅水模式下进行了同化试验。模式方程组为
| $\left\{ \begin{align} & \frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\frac{\partial \mathbf{u}}{\partial x}+\mathbf{v}\frac{\partial \mathbf{u}}{\partial y}-f\mathbf{v}=-g\frac{\partial \mathbf{h}}{\partial x}+\kappa {{\nabla }^{2}}\mathbf{u}+{{t}_{{{w}_{t}}}}\cdot {{\mathbf{G}}_{u}}({{\mathbf{u}}^{o}}-\mathbf{Hu}), \\ & \frac{\partial \mathbf{v}}{\partial t}+\mathbf{u}\frac{\partial \mathbf{v}}{\partial x}+\mathbf{v}\frac{\partial \mathbf{v}}{\partial y}+f\mathbf{u}=-g\frac{\partial \mathbf{h}}{\partial y}+\kappa {{\nabla }^{2}}\mathbf{v}+{{t}_{{{w}_{t}}}}\cdot {{\mathbf{G}}_{v}}({{\mathbf{v}}^{o}}-\mathbf{Hv}), \\ & \frac{\partial \mathbf{h}}{\partial t}+\mathbf{u}\frac{\partial \mathbf{h}}{\partial x}+\mathbf{v}\frac{\partial \mathbf{h}}{\partial y}=-\mathbf{h}(\frac{\partial \mathbf{u}}{\partial x}+\frac{\partial \mathbf{v}}{\partial y})+ \\ & \text{ }(\frac{\partial (\mathbf{u}{{\mathbf{h}}_{s}})}{\partial x}+\frac{\partial \mathbf{v}{{\mathbf{h}}_{s}}}{\partial y})+\kappa {{\nabla }^{2}}\mathbf{h}+{{t}_{{{w}_{t}}}}\cdot {{\mathbf{G}}_{h}}({{\mathbf{h}}^{o}}-\mathbf{Hh}), \\ \end{align} \right.$ | (16) |
其中,x、y、t的取值范围满足
| ${{\mathbf{h}}_{s}}={{\mathbf{h}}_{0}}\sin \left( {4\pi x}/{L}\; \right)\sin \left( {\pi y}/{D}\; \right)$ | (17) |
而为了模拟模式误差,在同化试验中将地形设置为
| ${{\mathbf{h}}_{s}}={{\mathbf{h}}_{0}}\sin \left( {4\pi x}/{L}\; \right)\sin \left( {\pi y}/{D}\; \right)\left[ 1.5\sin \left( {\pi x}/{L}\; \right) \right]$ | (18) |
两式中h0都取为200 m。对应的HBFNEnKF方法向前逼近模式方程和向后逼近模式方程分别为
| $\begin{align} & \frac{\partial {{\mathbf{u}}_{k}}}{\partial t}+{{\mathbf{u}}_{k}}\frac{\partial {{\mathbf{u}}_{k}}}{\partial x}+{{\mathbf{v}}_{k}}\frac{\partial {{\mathbf{u}}_{k}}}{\partial y}-f{{\mathbf{v}}_{k}}=-g\frac{\partial {{\mathbf{h}}_{k}}}{\partial x}+ \\ & \kappa {{\nabla }^{2}}{{\mathbf{u}}_{k}}+{{t}_{{{w}_{t}}}}\cdot {{\mathbf{G}}_{u}}({{\mathbf{u}}^{o}}-\mathbf{H}{{\mathbf{u}}_{k}}), \\ & \frac{\partial {{\mathbf{v}}_{k}}}{\partial t}+{{\mathbf{u}}_{k}}\frac{\partial {{\mathbf{v}}_{k}}}{\partial x}+{{\mathbf{v}}_{k}}\frac{\partial {{\mathbf{v}}_{k}}}{\partial y}+f{{\mathbf{u}}_{k}}=-g\frac{\partial {{\mathbf{h}}_{k}}}{\partial y}+ \\ & \kappa {{\nabla }^{2}}{{\mathbf{v}}_{k}}+{{t}_{{{w}_{t}}}}\cdot {{\mathbf{G}}_{v}}({{\mathbf{v}}^{o}}-\mathbf{H}{{\mathbf{v}}_{k}}), \\ & \frac{\partial {{\mathbf{h}}_{k}}}{\partial t}+{{\mathbf{u}}_{k}}\frac{\partial {{\mathbf{h}}_{k}}}{\partial x}+{{\mathbf{v}}_{k}}\frac{\partial {{\mathbf{h}}_{k}}}{\partial y}=-{{\mathbf{h}}_{k}}(\frac{\partial {{\mathbf{u}}_{k}}}{\partial x}+\frac{\partial {{\mathbf{v}}_{k}}}{\partial y})+ \\ & (\frac{\partial (\mathbf{u}{{\mathbf{h}}_{s}})}{\partial x}+\frac{\partial \mathbf{v}{{\mathbf{h}}_{s}}}{\partial y})+\kappa {{\nabla }^{2}}{{\mathbf{h}}_{k}}+{{t}_{{{w}_{t}}}}\cdot {{\mathbf{G}}_{h}}({{\mathbf{h}}^{o}}-\mathbf{H}{{\mathbf{h}}_{k}}), \\ & {{\mathbf{u}}_{k}}(x,y,0)={{{\mathbf{\tilde{u}}}}_{k-1}}(x,y,0), \\ & {{\mathbf{v}}_{k}}(x,y,0)={{{\mathbf{\tilde{v}}}}_{k-1}}(x,y,0), \\ & {{\mathbf{h}}_{k}}(x,y,0)={{{\mathbf{\tilde{h}}}}_{k-1}}(x,y,0), \\ \end{align}$ | (19) |
| $\begin{align} & \frac{\partial {{{\mathbf{\tilde{u}}}}_{k}}}{\partial t}+{{{\mathbf{\tilde{u}}}}_{k}}\frac{\partial {{{\mathbf{\tilde{u}}}}_{k}}}{\partial x}+{{{\mathbf{\tilde{v}}}}_{k}}\frac{\partial {{{\mathbf{\tilde{u}}}}_{k}}}{\partial y}-f{{{\mathbf{\tilde{v}}}}_{k}}=-g\frac{\partial {{{\mathbf{\tilde{h}}}}_{k}}}{\partial x}+ \\ & \kappa {{\nabla }^{2}}{{{\mathbf{\tilde{u}}}}_{k}}-{{t}_{{{w}_{t}}}}\cdot {{{\mathbf{{G}'}}}_{u}}({{\mathbf{u}}^{o}}-\mathbf{H}{{{\mathbf{\tilde{u}}}}_{k}}), \\ & \frac{\partial {{{\mathbf{\tilde{v}}}}_{k}}}{\partial t}+{{{\mathbf{\tilde{u}}}}_{k}}\frac{\partial {{{\mathbf{\tilde{v}}}}_{k}}}{\partial x}+{{{\mathbf{\tilde{v}}}}_{k}}\frac{\partial {{{\mathbf{\tilde{v}}}}_{k}}}{\partial y}+f{{{\mathbf{\tilde{u}}}}_{k}}=-g\frac{\partial {{{\mathbf{\tilde{h}}}}_{k}}}{\partial y}+ \\ & \kappa {{\nabla }^{2}}{{{\mathbf{\tilde{v}}}}_{k}}-{{t}_{{{w}_{t}}}}\cdot {{{\mathbf{{G}'}}}_{v}}({{\mathbf{v}}^{o}}-\mathbf{H}{{{\mathbf{\tilde{v}}}}_{k}}), \\ & \frac{\partial {{{\mathbf{\tilde{h}}}}_{k}}}{\partial t}+{{{\mathbf{\tilde{u}}}}_{k}}\frac{\partial {{{\mathbf{\tilde{h}}}}_{k}}}{\partial x}+{{{\mathbf{\tilde{v}}}}_{k}}\frac{\partial {{{\mathbf{\tilde{h}}}}_{k}}}{\partial y}=-{{{\mathbf{\tilde{h}}}}_{k}}(\frac{\partial {{{\mathbf{\tilde{u}}}}_{k}}}{\partial x}+\frac{\partial {{{\mathbf{\tilde{v}}}}_{k}}}{\partial y})+ \\ & (\frac{\partial (\mathbf{u}{{\mathbf{h}}_{s}})}{\partial x}+\frac{\partial \mathbf{v}{{\mathbf{h}}_{s}}}{\partial y})+\kappa {{\nabla }^{2}}{{{\mathbf{\tilde{h}}}}_{k}}-{{t}_{{{w}_{t}}}}\cdot {{{\mathbf{{G}'}}}_{h}}({{\mathbf{h}}^{o}}-\mathbf{H}{{{\mathbf{\tilde{h}}}}_{k}}), \\ & {{{\mathbf{\tilde{u}}}}_{k}}(x,y,T)={{\mathbf{u}}_{k}}(x,y,T), \\ & {{{\mathbf{\tilde{v}}}}_{k}}(x,y,T)={{\mathbf{v}}_{k}}(x,y,T), \\ & {{{\mathbf{\tilde{h}}}}_{k}}(x,y,T)={{\mathbf{h}}_{k}}(x,y,T), \\ \end{align}$ | (20) |
(19) 式中,x、y、t的取值范围满足
模式东西边界采用周期边界条件,上下边界设为0,初始高度场利用下式得到:
| $\begin{align} & \mathbf{h}(i,j)=H\{1+\left( {\mathbf{{y}'}(i)}/{\pi }\; \right)\exp (-2\mathbf{{y}'}{{(i)}^{2}})[1+ \\ & \text{ }0.1sin(4\pi {\mathbf{x}(j)}/{L}\;)]{{\}}^{-1}}, \\ \end{align}$ | (21) |
其中,i、j满足的取值范围为
同化试验使用了50个集合,其构造方式为:在初始高度场上叠加满足分布的扰动,然后利用地转关系计算出对应风场集合成员。真实场和集合成员都经过60 h的启动时间(spin up),同时也是对集合成员的发展。同化时间间隔分为24 h一次和48 h一次两种。生成含误差观测资料的方法为:将高度场h和风场u、v三个变量的真值插值到模式空间中120个不规则分布点上,再分别叠加满足分布(高度场)的扰动和满足分布(风场)的扰动得到。
试验中所用同化方案为EnSRF、HNEnKF以及HBFNEnKF,并另外进行一次模式自由积分作为控制试验(CTRL)。所有同化试验均采用GC(Gaspari and Cohn, 1999)局地化方法进行局地化处理,局地化半径取为600 km;同时采用松弛膨胀法进行协方差膨胀(relax inflation)(Zhang et al., 2004),膨胀系数设置为0.1。利用本文前述的时间权重算子,将HBFNEnKF和HNEnKF中的Nudging项分配到以观测资料加入时次为中心的、左右各1 h的时间窗口内。
为了检验各方案同化过程中变量间的平衡性,上述试验均关闭了EnSRF同化中的多变量分析。所谓多变量分析,指集合卡尔曼滤波通过背景误差协方差,在同化时实现各模式变量相互影响;关闭多变量分析,即进行单一变量要素同化试验。为了进一步检验新方案的效果,本文还在全球浅水模式中进行了考虑多变量分析后的同化试验。全球浅水模式纬向格点180个,经向格点90个,积分步长60 s,模式初始场设置参见Nair et al.(2005)。观测资料取为405个不规则分布的点。各试验组都取20个集合成员,局地化半径为50 km,协方差膨胀系数为0.3。在全球浅水模式试验中,首先让模式积分10 d作为spin up并发展集合成员,再进行3 d、每6 h一次的同化循环,之后再进行4 d的自由积分。
| 表 1 通道浅水模式中各试验组名称及设置 Table 1 Names and designs of experiments in the channel shallow water model |
| 表 2 全球浅水模式中各试验组名称及设置 Table 2 Names and designs of experiments in the global shallow water model |
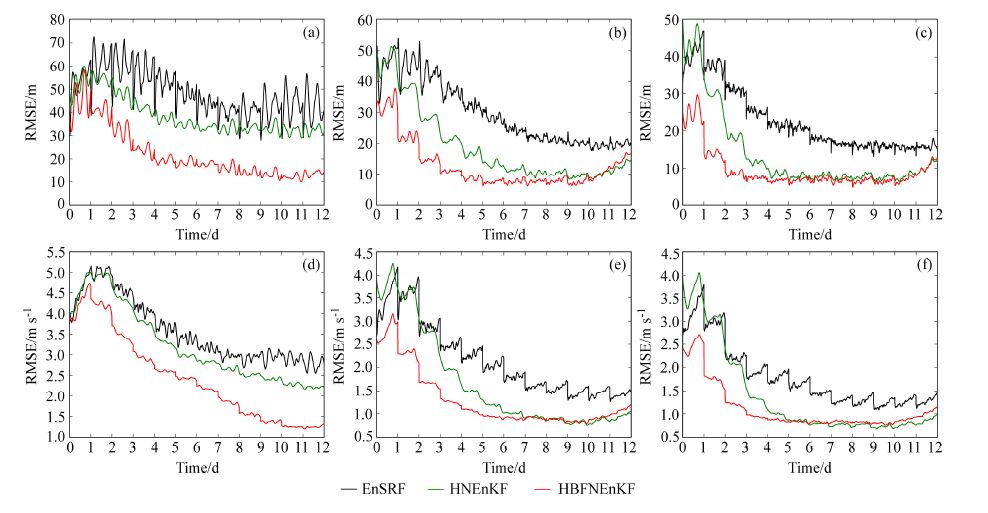
图 4是同化间隔为24 h的高度场、风场均方根误差(RMSE)随时间的变化趋势。图 4a、b、c分别为仅同化高度场、仅同化风场、同时同化高度场和风场时的高度场RMSE变化;图 4d、e、f为对应的风场RMSE变化。由于与Nudging混合,HNEnKF和HBFNEnKF方法单次同化增量很小,这里给出的是每一积分步的RMSE。可以明显看出,不论是同化单一变量观测还是同时同化高度场和风场观测,HBFNEnKF的同化效果都是最好的。
|
图 4 通道浅水模式下各同化方案高度场的RMSE随时间的变化:(a)只同化高度场;(b)只同化风场;(c)同时同化高度场和风场。(d-f)同(a-c),但为风场的RMSE变化 Figure 4 Evolution of RMSE of height using single variable analysis in the channel shallow water model: (a) Only height observations are assimilated, (b) only wind observations are assimilated, (c) both wind and height observations are assimilated. (d-f) As in (a-c), but for RMSE of wind |
当仅同化高度场时(图 4a),各方案的同化效果都较差,但EnSRF在每个同化时刻后都有很强的波动,其RMSE有先增大再逐渐减小的变化过程;同样的现象也出现在图 4b中。这是由于只采用了单变量分析,EnSRF同化不能很好地使模式各变量之间达到平衡关系,需要一段时间的spin up。该问题并未出现在HNEnKF和HBFNEnKF试验中,不论是只同化高度场资料还是只同化风场资料,两种混合方法都能保持较好的同化连续性,并维持模式各变量间的平衡关系。由图 4a和图 4d可见,由于只同化了高度场资料,HNEnKF虽然比EnSRF的同化效果好,但其优势并不明显,且需要在积分一段时间后,才能加大与EnSRF同化间的差距;而HBFNEnKF不但能迅速订正高度场,同时能很好地改善风场。这说明经过前后积分迭代,HBFNEnKF比HNEnKF能更好地进行观测资料和模式变量间的调整。
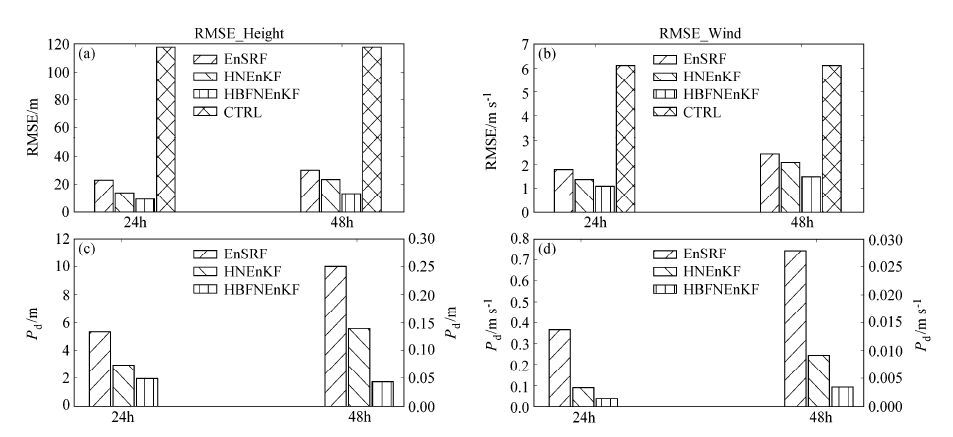
图 5为模式循环同化期间,各同化方法在不同同化时间间隔情况下时间平均的RMSE和不连续性参数Pd(discontinue parameter)的对比。这里Pd为Lei et al.(2012a,2012b)引入的参数,目的是为了检验某一同化方法的同化连续性。其计算公式为
| ${{P}_{d}}=\frac{1}{m}\sum\limits_{i}{|{{E}_{i-1}}-{{E}_{i}}|}$ | (22) |
其中,m为试验中同化时刻的总次数,Ei-1和Ei分别表示某同化时刻同化前和同化后的RMSE。Pd值越大则说明连续性越差。
|
图 5 模式循环同化期间平均的(a)高度场、(b)风场的RMSE和(c)高度场、(d)风场的Pd分布示意图。(c)、(d)中,HNEnKF和HBFNEnKF试验的值在右侧坐标中显示 Figure 5 Average (a, b) RMSE during assimilation cycle and (c, d) discontinue parameter (Pd) from each assimilation scheme: (a, c) Height; (b, d) wind. Axis for HNEnKF and HBFNEnKF experiments in (c, d) is on the right |
由图 5a、b可见,HBFNEnKF试验的时间平均RMSE最小,HNEnKF试验次之,EnSRF试验最大。随着同化时间间隔的增大,各同化方法的RMSE都有增加,其中变化最明显的是HNEnKF方法,而同样条件下HBFNEnKF方案的RMSE增幅并不明显。根据同化间隔为48 h时的RMSE变化曲线(图略)可知,相比间隔时间为24 h的情况,各同化方法的均方根误差收敛时间都有增加,这是时间平均RMSE增加的主要原因,但其中以HBFNEnKF方法的收敛时间变化最小。此外,HNEnKF与EnSRF之间的RMSE差距明显减小。Lei et al.(2012a,2012b)指出这是因为时间窗口增大,Nudging同化受到更多模式误差带来的影响。而采用前后积分迭代进行多次调整,HBFNEnKF在一定程度上改善了HNEnKF这一缺点。由图 5c 、d可见,HBFNEnKF同化也保留了HNEnKF良好的同化连续性;与他们相比,EnSRF的同化连续性最差。
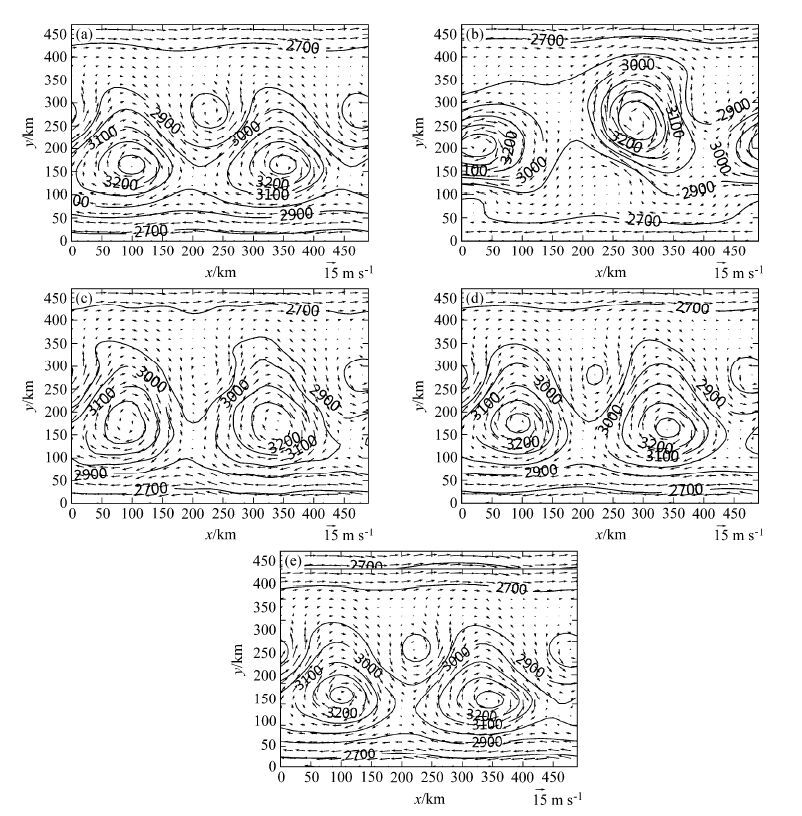
图 6为同化时间间隔24 h,只同化风场资料时,各试验循环同化结束后的环流形势。可以看出,循环同化结束后模式场中主要的系统是位于y=15 km处的两个高压中心以及位于y=30 km处的两个小低压。由图 6c、d、e可见,EnSRF试验未能将y=30 km处的小低压模拟出来。同时两个高压中心的强度、位置以及等高线的流形都与真实场存在一定差异。虽然没有模拟出低压中心,但是在真实场中小低压的位置(y=30 km,x=20 km),EnSRF模拟出了气旋性环流。这说明EnSRF同化风场资料时,不能很好地调整模式高度场。由图 6d可见,相比于EnSRF,HNEnKF有一定改进,但依然不足;同化效果最好的是HBFNEnKF试验,从各环流系统的强度、位置分布看,HBFNEnKF都有与真实场最接近的结果。
|
图 6 只同化风场、同化周期24 h时,各试验循环同化结束后高度场(单位:m)和风场(单位:m s−1):(a)真实场;(b)控制试验;(c)EnSRF;(c)HNEnKF;(e)HBFNEnKF Figure 6 Height (units: m) and wind (units: m s−1) fields after assimilation cycle by setting the time window to 24 h when only wind observations were assimilated: (a) Real field; (b) control; (c) EnSRF; (d) HNEnKF; (e) HBFNEnKF |
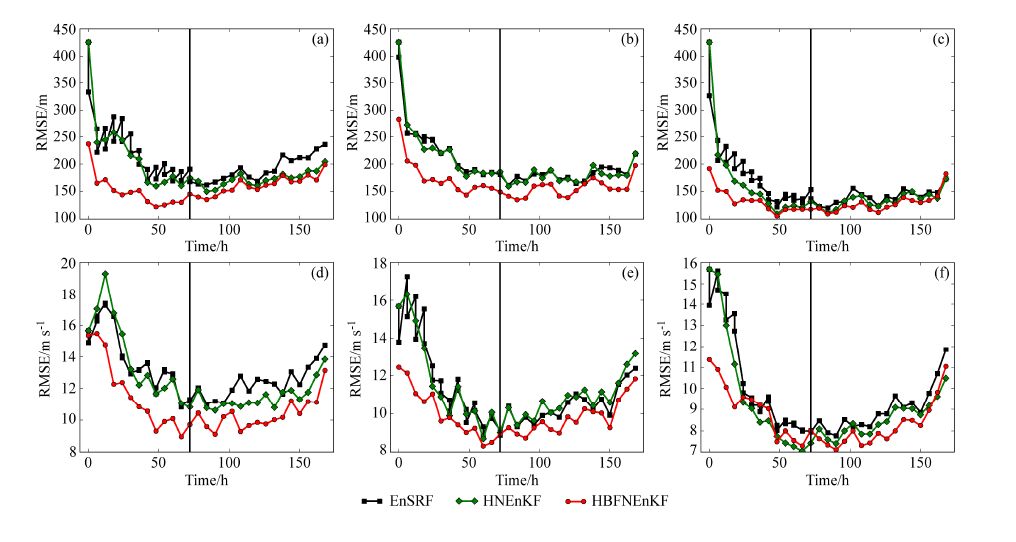
图 7给出的是考虑了多变量分析,各同化方案在全球浅水模式同化试验中RMSE的变化趋势。由于全球浅水模式试验积分步较多,所以制作插图时只考虑了同化时刻。可以明显发现,在考虑多变量分析后,EnSRF方案的同化效果得到了很大改进。然而其同化不连续、不平衡的现象依然存在。在3 d的循环同化(图中黑色竖线)后,EnSRF试验的RMSE有较快增加;而从整体来看,HNEnKF和HBFNEnKF在自由积分阶段的RMSE都比EnSRF低。从整体来看,HBFNEnKF依然保留了收敛快、同化效果好、RMSE低的特点。不论是同化单一观测变量还是同时同化风场和高度场变量,HBFNEnKF都能保持最小的均方根误差。尤其是在只同化风场观测和只同化高度场观测时,HBFNEnKF对非观测模式变量能有较好订正(图 7b、d)。
|
图 7 全球浅水模式下各同化方案高度场的RMSE 随时间的变化:(a)只同化高度场;(b)只同化风场、(c)同时同化风场和高度场观测。(d-f)同 (a-c),但为风场的RMSE 变化 Figure 7 Evolution of RMSE of height using single variable analysis in the global shallow water model: (a) Only height observations are assimilated, (b) only wind observations are assimilated, (c) both wind and height observations are assimilated. (d-f) As in (a-c), but for RMSE of wind |
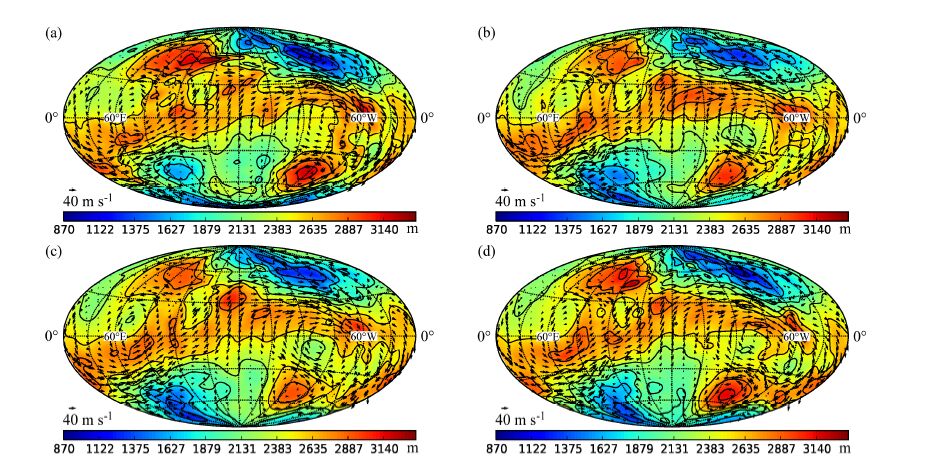
均方根误差只是对同化效果整体情况的反映。图 8、9给出了在全球浅水模式中各试验循环同化结束时,且自由积分4 d后的环流形势(180°为图的中心经度)。图 8是只同化风场观测的结果;图 9为只同化高度场观测的结果。
|
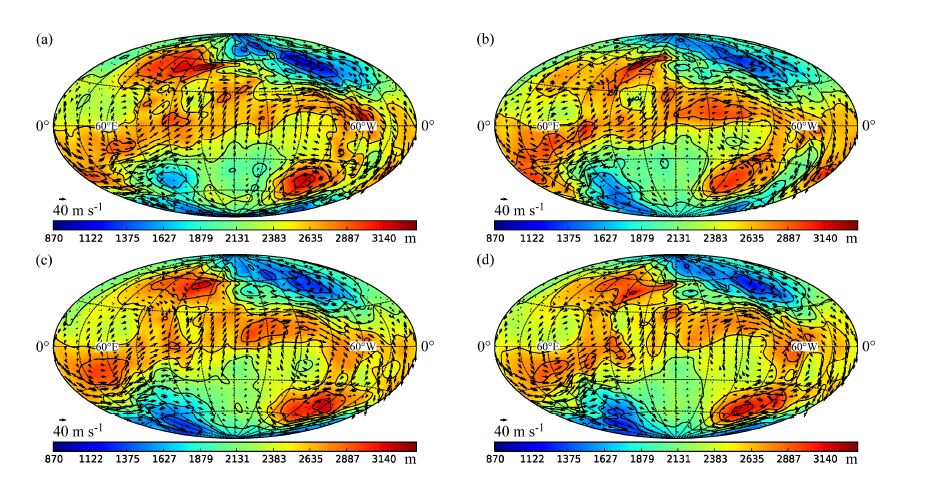
图 8 全球浅水模式下只同化风场资料时,各同化方案循环同化结束后,并自由积分4 天后的环流形势:(a)真实场;(b)EnSRF;(c)HNEnKF; (d)HBFNEnKF。彩色阴影代表位势高度(单位:m),黑色线代表等高线(单位:m),箭头代表风场(单位:m s−1) Figure 8 Height and wind fields after assimization cycle and 4 days integration in the global shallow water model when only wind observations were assimilated: (a) Real field; (b) EnSRF; (c) HNEnKF; (d) HBFNEnKF. Shadings represent geopotential height (units: m); black lines represent contours (units: m); arrows represent the wind field |
由图 8可见,当只同化风场资料时,HBFNEnKF相对于另外两个试验,在各环流系统中心的强度和位置上都与真实场最为接近,较好地模拟出了位于30°~60°N的一高一低两个环流中心,以及位于30°~60°S、120°W处的高压中心。HNEnKF和EnSRF试验在30°N、150°W处模拟出了一个虚假的高压中心,而HBFNEnKF试验的模拟结果则没有出现这样的虚假高压中心。就风场的分布和强度来说,HBFNEnKF的同化效果也优于另外两种方案。
由图 9可见,当只同化高度场资料时,EnSRF和HNEnKF试验模拟结果中的虚假环流系统发展得更为明显。相比只同化风场的试验,由于观测资料和观测变量的减少,HBFNEnKF同化效果有一定程度的降低。尽管如此,试验HBFNEnKF模拟的主要环流系统及其强度与位置依然优于另外两组试验。
4.3 增量场分析本节将通过增量场的分析简单说明,相比EnSRF,HBFNEnKF能够取得更好的同化效果,同时还能避免一些虚假环流系统的出现。 由于HBFNEnKF能够通过反向积分回到初始时刻,求得对应时刻同化前后的增量,而HNEnKF仅为向前积分且单次同化增量过小,无法进行比较,所以这里只用HBFNEnKF与EnSRF进行对比。
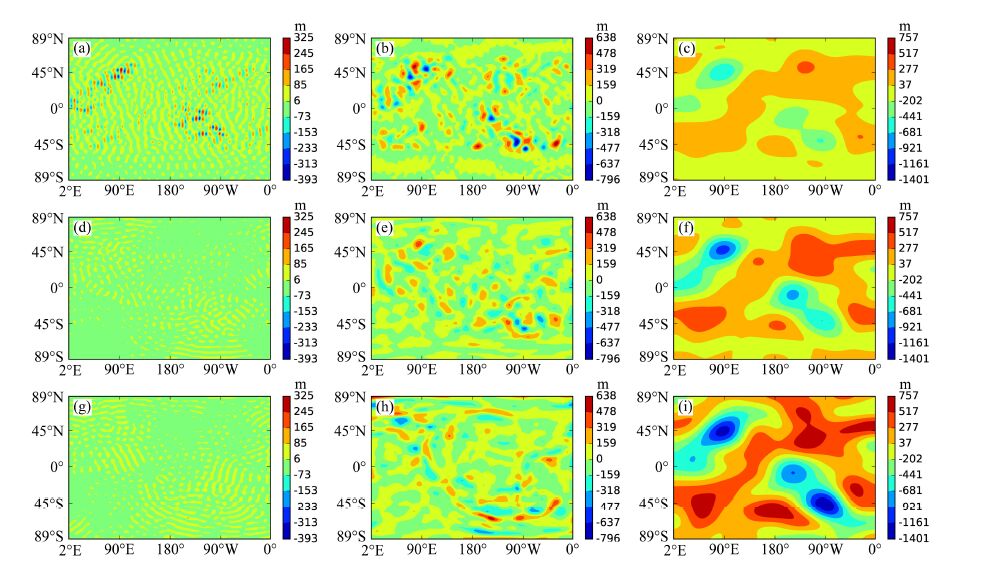
首先利用离散余弦变化(DCT)(Denis et al., 2002)将EnSRF、HBFNEnKF以及真实场在模式初始时刻的高度场转换到波数空间,然后利用带通滤波对其进行尺度分离,最后求得各尺度上的增量场。图 10为第一个同化时刻、同时同化高度场和风场时,经过尺度分离后,EnSRF和HBFNEnKF
|
图 10 全球浅水模式下第一个同化时刻同时同化高度场和风场时,(a)EnSRF、(d)HBFNEnKF、(g)真实场与控制试验在小尺度范围上高度场的差异。(b、e、h)同(a、d、g),但为在中尺度范围上的差异场;(c、f、i)同(a、d、g),但为在大尺度范围上的差异场 Figure 10 Distribution of height differences for the small scale between the control test and (a) EnSRF experiment, (d) HBFNEnKF experiment, (g) the real field at the first assimilation time when height and wind observations are assimilated in the global shallow water model. (b, e, h) As in (a, d, g), but for the mesoscale.(c, f, i) As in (a, d, g), but for the large scale |
高度场的增量场以及真实场与相应时刻控制试验的差异场(因为是第一个同化时刻,所以EnSRF和HBFNEnKF同化前的背景场与相应时刻的控制试验是相同的),在小尺度、中尺度以及大尺度范围内的差异分布。可以发现:在大尺度范围(图 10c、f、i),不论是增量的强度还是分布位置,HBFNEnKF都比EnSRF更接近真实场;在中尺度范围(图 10b、e、h),虽然HBFNEnKF的增量场与真实场和控制试验的差异场没有很好的匹配,但是与EnSRF的增量场相比,避免了许多虚假增量的出现;在小尺度范围(图 10a、d、g),HBFNEnKF的增量场与真实场和控制试验的差异场分布较为一致,EnSRF有明显的虚假增量,这正是由于EnSRF同化不平衡、不连续所致。
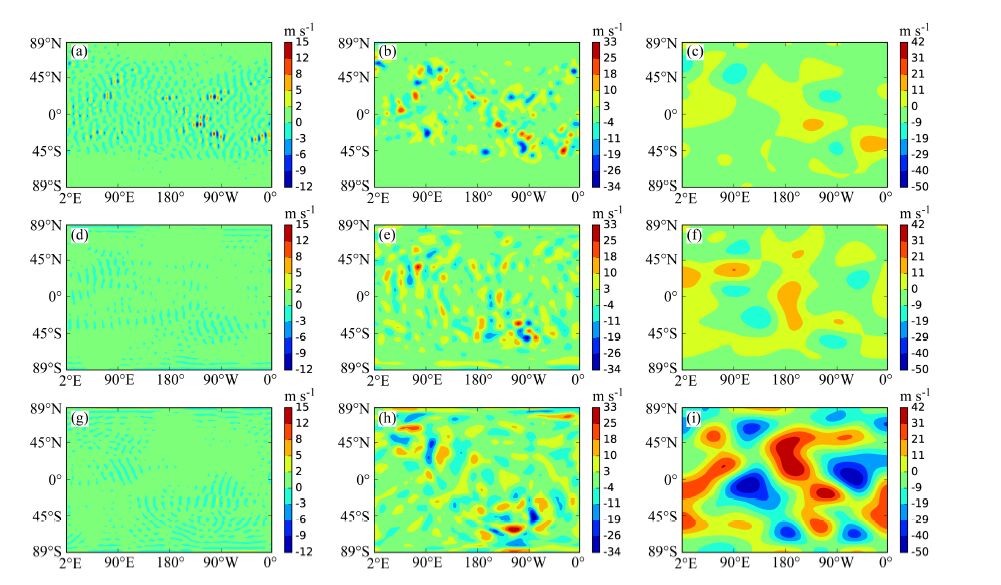
图 11为第一个同化时刻、只同化高度场时,进行了尺度分离后,EnSRF、HBFNEnKF以及真实场的纬向风分量与控制试验的差异场。只同化高度场是为了使差异更加明显,同时体现同化方案对非观测模式变量的订正效果。可以发现:在大尺度范围,HBFNEnKF有着与真实场更为一致的增量分布;而在中尺度尤其是小尺度范围,HBFNEnKF避免了在EnSRF同化中出现的虚假增量。这说明,在对非观测模式变量的订正上,HBFNEnKF有比EnSRF更优秀的能力,同时能解决EnSRF同化中的虚假相关问题。
|
图 11 同图 10,但为只同化高度场时纬向风分量的结果 Figure 11 As in Fig. 10,but for zonal wind when only height observations were used |
综上所述,HBFNEnKF同化能在模式大尺度范围进行更好的同化,同时在中小尺度范围能够避免传统EnSRF同化中虚假相关的出现。这也正是HBFNEnKF有比EnSRF更好的同化效果、并能够避免模式结果中虚假环流系统出现的原因。
5 结论与讨论本文基于Lei et al.(2012a,2012b)设计的HNEnKF同化方法和Auroux and Blum(2005,2008)设计的BFN方法,通过结合BFN和EnKF同化算法,设计了HBFNEnKF混合同化方案,并针对EnSRF、HNEnKF和HBFNEnKF三种算法,在考虑了误差的通道浅水模式、全球浅水模式中进行同化试验。试验对比了在单变量分析、多变量分析情况下,这三种同化方法的RMSE变化、不连续性参数分布以及经过循环同化并自由积分后的模式环流形势,得出以下结论:
(1) HBFNEnKF混合同化方案保留了HNEnKF同化的连续性和平滑性,解决了EnSRF同化不连续、不平滑的缺点。
(2) 通过前后迭代积分,HBFNEnKF充分发挥了Nudging同化的特点:积分时间越长同化效果越好,使得同化能很快收敛,相比EnSRF和HNEnKF有最快的收敛速度,同时取得了更好的同化效果。而通过前后积分迭代,HBFNEnKF能较好地逼近真实场,并在一定程度上改善了HNEnKF同化效果随着同化时间间隔增加而降低的问题。
(3) 由于HBFNEnKF作用于模式积分,所以HBFNEnKF同化能利用模式方程进行约束,使得变量间的平衡得以维持。在单变量分析试验中,HBFNEnKF和HNEnKF都能较好地利用观测资料对各模式变量进行订正。而相比之下,由于没有考虑多变量分析,EnSRF方法在同化单一变量时带来了较大的模式扰动,增加了模式的spin up时间,从而影响了同化效果。
(4) 全球浅水模式的试验表明,在经过4 d自由积分后,HBFNEnKF不但更加接近真实场,同时也避免了一些虚假环流系统的出现。通过对高度场增量的尺度分析发现,这是由于HBFNEnKF在大尺度范围有比EnSRF更好的同化效果:其增量场在强度和空间上都更加接近同化前与真实场的差异场。在中小尺度范围,HBFNEnKF还避免了一些虚假增量的出现,这正是由于HBFNEnKF较好的同化连续性和平滑性所致。仅同化高度场时,纬向风增量的尺度分析也有一致结论,这是HBFNEnKF能够较好地维持模式变量间相互平衡、对非观测模式变量能进行合理调整的证明。
尽管HBFNEnKF在本次试验中有最佳的效果,但是浅水模式只是一个二维理想模式,并不能完全代表真实大气的运动与结构。HBFNEnKF同化方法在多层模式以及实际预报模式中的试验将在之后进行,对真实观测资料的同化效果也有待检验。另外,HBFNEnKF的许多特性还有待进一步探讨,如:HBFNEnKF是否也保留了BFN能将大气低层资料同化到模式高层的特性?迭代过程中β的选取对同化效果有何影响?此外,Lorenz 96模式的试验结果(略)表明,通过引入不随时间变化的部分,能够进一步增加HBFNEnKF的同化效果,这一改进是否能在更为复杂的模式中实现?同时,HBFNEnKF还存在由于迭代带来的更多计算量,以及向后积分不稳定等问题,虽然在本文试验中并未出现上述情况,但依然应该进行相应的研究和改进。
| [1] | Anderson J L. 2001. An ensemble adjustment Kalman filter for data assimilation[J]. Mon. Wea. Rev. , 129(12) : 2884–2903, doi:10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2 |
| [2] | Auroux D. 2009. The back and forth nudging algorithm applied to a shallow water model, comparison and hybridization with the 4D-VAR[J]. Int. J. Numer. Methods Fluids , 61(8) : 911–929, doi:10.1002/fld.1980 |
| [3] | Auroux D, Blum J. 2005. Back and forth nudging algorithm for data assimilation problems[J]. Comptes Rendus Mathematique , 340(12) : 873–878, doi:10.1016/j.crma.2005.05.006 |
| [4] | Auroux D, Blum J. 2008. A nudging-based data assimilation method: The Back and Forth Nudging (BFN) algorithm[J]. Nonlin. Processes Geophys. , 15(2) : 305–319, doi:10.5194/npg-15-305-2008 |
| [5] | Bishop C H, Etherton B J, Majumdar S J. 2001. Adaptive sampling with the ensemble transform Kalman filter. Part I: Theoretical aspects[J]. Mon. Wea. Rev. , 129(3) : 420–436, doi:10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2 |
| [6] | Bloom S C, Takacs L L, da Silva A M, et al. 1996. Data assimilation using incremental analysis updates[J]. Mon. Wea. Rev. , 124(6) : 1256–1271, doi:10.1175/1520-0493(1996)124<1256:DAUIAU>2.0.CO;2 |
| [7] | Boilley A, Mahfouf J F. 2012. Assimilation of low-level wind in a high-resolution mesoscale model using the back and forth nudging algorithm[J]. Tellus A , 64 : 18697, doi:10.3402/tellusa.v64i0.18697 |
| [8] | Denis B, Côté J, Laprise R. 2002. Spectral decomposition of two-dimensional atmospheric fields on limited-area domains using the discrete cosine transform (DCT)[J]. Mon. Wea. Rev. , 130(7) : 1812–1829, doi:10.1175/1520-0493(2002)130<1812:SDOTDA>2.0.CO;2 |
| [9] | Evensen G. 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. J. Geophys. Res. , 99(C5) : 10143–10162, doi:10.1029/94JC00572 |
| [10] | Evensen G. 2003. The ensemble Kalman filter: Theoretical formulation and practical implementation[J]. Ocean Dynamics , 53(4) : 343–367, doi:10.1007/s10236-003-0036-9 |
| [11] | Evensen G, van Leeuwen P J. 2000. An ensemble Kalman smoother for nonlinear dynamics[J]. Mon. Wea. Rev. , 128(6) : 1852–1867, doi:10.1175/1520-0493(2000)128<1852:AEKSFN>2.0.CO;2 |
| [12] | Gaspari G, Cohn S E. 1999. Construction of correlation functions in two and three dimensions[J]. Quart. J. Roy. Meteor. Soc. , 125(554) : 723–757, doi:10.1002/qj.49712555417 |
| [13] | Hoke J E, Anthes R A. 1976. The initialization of numerical models by a dynamic-initialization technique[J]. Mon. Wea. Rev. , 104(12) : 1551–1556, doi:10.1175/1520-0493(1976)104<1551:TIONMB>2.0.CO;2 |
| [14] | Kepert J D. 2009. Covariance localisation and balance in an ensemble Kalman filter[J]. Quart. J. Roy. Meteor. Soc. , 135(642) : 1157–1176, doi:10.1002/qj.443 |
| [15] | Lakshmivarahan S, Lewis J M. 2013. Nudging methods: A critical overview [M]//Park S K, Xu L. Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. Ⅱ). Springer: Berlin Heidelberg, 27-57, doi:10.1007/978-3-642-35088-7_2. |
| [16] | Lei L L, Stauffer D R, Haupt S E, et al. 2012a. A hybrid nudging-ensemble Kalman filter approach to data assimilation. Part I: Application in the Lorenz system[J]. Tellus A , 64 : 18484, doi:10.3402/tellusa.v64i0.18484 |
| [17] | Lei L L, Stauffer D R, Deng A J. 2012b. A hybrid nudging-ensemble Kalman filter approach to data assimilation. Part Ⅱ: Application in a shallow-water model[J]. Tellus A , 64 : 18485, doi:10.3402/tellusa.v64i0.18485 |
| [18] | Lewis J M, Lakshmivarahan S, Dhall S.2006. Dynamic Data Assimilation: A Least Squares Approach[M]. Cambridge, UK and New York, NY, USA: Cambridge University Press . |
| [19] | Liu Y B, Bourgeois A, Warner T, et al. 2005. Implementation of observation-nudging based FDDA into WRF for supporting ATEC test operations [R]. 2005 WRF User Workshop. Paper 10.7. |
| [20] | Liu Y B, Bourgeois A, Warner T, et al. 2006. An update on "obs-nudge"-based FDDA for WRF-ARW: Verification using OSSE and performance of real-time forecasts [R]. 2006 WRF User Workshop. Paper 4.7. |
| [21] | Livings D. 2005. Aspects of the ensemble Kalman filter [D]. M. S. thesis, Reading University. |
| [22] | 闵锦忠, 王世璋, 陈杰, 等. 2012. 迭代EnSRF方案设计及在Lorenz96模式下的检验[J]. 大气科学 , 36 (5) : 889–900, doi:10.3878/j.issn.1006-9895.2012.11185 Min Jinzhong, Wang Shizhang, Chen Jie, et al. 2012. The implementation and test of iterative EnSRF with Lorenz96 model[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 36(5) : 889–900, doi:10.3878/j.issn.1006-9895.2012.11185 |
| [24] | Nair R D, Thomas S J, Loft R D. 2005. A discontinuous Galerkin global shallow water model[J]. Mon. Wea. Rev. , 133(4) : 876–888, doi:10.1175/MWR2903.1 |
| [25] | Ourmières Y, Brankart J M, Berline L, et al. 2006. Incremental analysis update implementation into a sequential ocean data assimilation system[J]. J. Atmos. Oceanic Technol. , 23(12) : 1729–1744, doi:10.1175/JTECH1947.1 |
| [26] | Ruggiero G A, Ourmières Y, Cosme E, et al. 2015. Data assimilation experiments using the diffusive back-and-forth nudging for the NEMO ocean model[J]. Nonlin. Processes Geophys. , 22(2) : 233–248, doi:10.5194/npg-22-233-2015 |
| [27] | 邵长亮, 闵锦忠. 2015. 集合均方根滤波同化地面自动站资料的技术研究[J]. 大气科学 , 39 (1) : 1–11, doi:10.3878/j.issn.1006-9895.1406.13263 Shao Changliang, Min Jinzhong. 2015. A study of the assimilation of surface automatic weather station data using the ensemble square root filter[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 39(1) : 1–11, doi:10.3878/j.issn.1006-9895.1406.13263 |
| [29] | Stauffer D R, Seaman N L. 1990. Use of four-dimensional data assimilation in a limited-area mesoscale model. Part I: Experiments with synoptic-scale data [J]. Mon. Wea. Rev. , 118(6) : 1250–1277, doi:10.1175/1520-0493(1990)118<1250:UOFDDA>2.0.CO;2 |
| [30] | Stauffer D R, Bao J W. 1993. Optimal determination of nudging coefficients using the adjoint equations[J]. Tellus A , 45(5) : 358–369, doi:10.1034/j.1600-0870.1993.t01-4-00003.x |
| [31] | 王世璋, 闵锦忠, 陈杰, 等. 2013. 迭代集合平方根滤波在风暴尺度资料同化中的应用[J]. 大气科学 , 37 (3) : 563–578, doi:10.3878/j.issn.1006-9895.2012.11186 Wang Shizhang, Min Jinzhong, Chen Jie, et al. 2013. Application of iterative ensemble square-root filter in storm-scale data assimilation[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 37(3) : 563–578, doi:10.3878/j.issn.1006-9895.2012.11186 |
| [33] | Whitaker J S, Hamill T M. 2002. Ensemble data assimilation without perturbed observations[J]. Mon. Wea. Rev. , 130(7) : 1913–1924, doi:10.1175/1520-0493(2002)130<1913:EDAWPO>2.0.CO;2 |
| [34] | Yang S C, Corazza M, Carrassi A, et al. 2009. Comparison of local ensemble transform Kalman filter, 3DVAR, and 4DVAR in a quasigeostrophic model[J]. Mon. Wea. Rev. , 137(2) : 693–709, doi:10.1175/2008MWR2396.1 |
| [35] | Zhang F, Snyder C, Sun J Z. 2004. Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter[J]. Mon. Wea. Rev. , 132(5) : 1238–1253, doi:10.1175/1520-0493(2004)132<1238:IOIEAO>2.0.CO;2 |
| [36] | Zou X, Navon I M, Ledimet F X. 1992. An optimal nudging data assimilation scheme using parameter estimation[J]. Quart. J. Roy. Meteor. Soc. , 118(508) : 1163–1186, doi:10.1002/qj.49711850808 |
 2016, Vol. 40
2016, Vol. 40