2 中国气象科学研究院灾害天气国家重点实验室, 北京 100081
3 中国气象局气象干部培训学院四川分院, 成都 610072
2 State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
3 Sichuan Branch, China Meteorological Administration Training Centre, Chengdu 610027
中国气象局自主研发的全球、区域多尺度通用同化与数值预报系统——GRAPES模式系统 (Global/ Regional Assimilation and PrEdiction System;陈德辉和沈学顺,2006;陈德辉等,2008;张人禾和沈学顺,2008) 分为全球和区域模式版本,包含了资料同化、动力模式和分析处理功能,全球和区域模式都已经在国家业务中心业务化运行。GRAPES全球模式计划将承担我国的中期数值预报业务,并向高分辨预报应用发展,模式包含了较为详细的辐射传输、大气边界层、积云对流和云微物理过程计算方案,预报效果不断改进。针对我国天气受青藏高原大地形和复杂下垫面影响较大、以及模式中地形处理存在的问题,徐国强等 (2010)在模式中引进地形重力波拖拽参数化,处理地形重力波对动量传输的影响,改善了东亚地区预报效果。考虑未来的高分辨应用,Li at al.(2015) 新引入了球面准均匀网格——阴阳网格体系,优化全球模式的动力计算性能和计算效率。
除了数值模式自身的动力、物理过程误差及非线性大气的不确定性问题之外,由于观测资料误差、背景信息不准确等形成的初始场误差和模式上下边界的不确定性等,数值预报存在系统性误差和随机误差。正是由于初始场误差、模式误差、大气的非线性特征和数值模式“spin-up”现象的存在,数值预报表现出对重大转折性天气、突发性中小尺度强对流暴雨预报的困难,陈德辉和薛纪善 (2004)也曾指出对3 h内和7 d以上时效的预报能力还不能满足要求,而这两个时段正是临近预报和延伸期预报关注的关键预报时效。从模式误差积累来看,GRAPES全球模式的误差随着分辨率降低而线性增加 (庄照荣等,2010),且随预报时效增加而增长,且由于误差积累,影响辐射过程计算稳定性 (杨学胜等,2009),并在青藏高原区域表现出明显误差。改进模式预报性能可以从模式自身改造和模式结果订正两个途径来实现,如提高模式离散化精度、改进模式物理过程表达、以及提高初始场质量等都归于第一种方法,而通过对模式预报产品的进一步加工 (产品释用) 来改善数值模式的确定性预报水平 (翟盘茂等,2013),通过统计方法对模式动力预报结果修正获得动力—统计预报 (丑纪范,1986),如在模式预报基础上的MOS (Model Output Statistics) 线性回归方法、Kalman滤波等则属于第二种。
目前,我们已有大量实际观测数据、遥感数据和再分析资料的积累,顾震潮 (1958)指出观测资料提供了大气实际运动状态的最真实描述,这些历史资料的应用可以克服单一动力模式存在的缺陷 (丑纪范,1986),其应用方法包括根据历史观测资料反演优化模式参数 (邱崇践和丑纪范,1990;丑纪范和任宏利,2006;丑纪范,2007)、通过模式反问题求解估算不同时刻模式误差 (达朝究,2011)、利用历史相似信息估算模式误差 (Huang et al., 1993;任宏利和丑纪范,2005) 等。这种相似性误差订正方法,利用历史相似信息提供的误差预测模式预报的误差,包含了相似初值流型的模式误差演变信息,可用来订正预报结果,具有良好的可移植性。最近,基于对过去资料的应用和预报量的物理分解概念 (钱维宏,2012),Peng et al.(2013)提出了基于历史资料的模式距平积分预报订正ANO (Anomaly Numerical-correction with Observations) 方法,并应用于CAM3.0大气环流模式对2008年1月雨雪冰冻灾害天气过程的预报订正,效果显著。常俊等 (2015)采用WRF (Weather Research and Forecasting model) 模式对2014年7月四川盆地存在强烈时空不连续降水过程的要素订正效果也取得显著效果,并首次验证了该方法对降水预报的订正效果。
为了解GRAPES模式的系统误差分布,改善模式全球中期预报效果,本研究以ERA-interim再分析资料为初始场,采用GRAPES全球模式对1984~2014年间7月的31个个例进行了10 d后报,首先对模式误差分布形态分析评估,然后尝试用ANO方法对预报结果进行订正,为模式提供一套可行的产品释用工具,以提高模式的中期预报水平。
2 资料再分析资料是在数值模式动力过程控制下对多种观测资料的同化分析结果,被认为是实际大气状态的最佳描述,被广泛应用于天气过程分析和数值模拟研究的模式初始场。本文选用欧洲中期天气预报中心 (ECMWF) 的ERA-interim再分析资料作为模式初值和历史“实况”资料,其水平空间分辨率为1.0°×1.0°,全球361×180个格点,垂直方向从1000~1 hPa共分37层,时间间隔6 h,每日4次,变量包括位势高度Hgt、温度T、水平风速u和v、比湿q以及地表温度Ts和地面气压ps等。考虑到计算能力限制,本文针对1984~2014年的31年间夏季7月15~24日的预报结果进行分析订正和讨论。
3 GRAPES全球模式预报误差评估 3.1 GRAPES全球模式简介GRAPES全球数值预报模式系统是一个全球、完全可压、非静力大气动力模式,采用半隐式半拉格朗日方法进行数值求解,具有很好的计算稳定性。变量水平分布为Arakawa C跳点网格,在垂直方向采用Charney-Philips跳层设置。垂直坐标采用高度地形追随坐标,并采用半隐式半拉格朗日方法积分求解,使用矢量场离散化技术来计算曲率项和解决两极地区的矢量计算问题,包括了辐射、积云对流、云微物理、边界层垂直扩散、陆面过程等完整的物理过程参数方案。本文的后报试验模式水平分辨率为1°×1°,垂直方向为不等距61层,模式层顶1 hPa。
除三阶精度半拉格朗日计算外,模式的离散化采用了准二阶方案,同时在模式上下边界处理过程中会引入一阶误差。物理过程参数化的不确定性普遍存在,特别是各种方案的针对性调整对反映东亚季风环境的次网格尺度过程非常必要,但误差形态无法确定。这里我们参考再分析资料为“实况”,对GRAPES模式的总体误差进行评估。
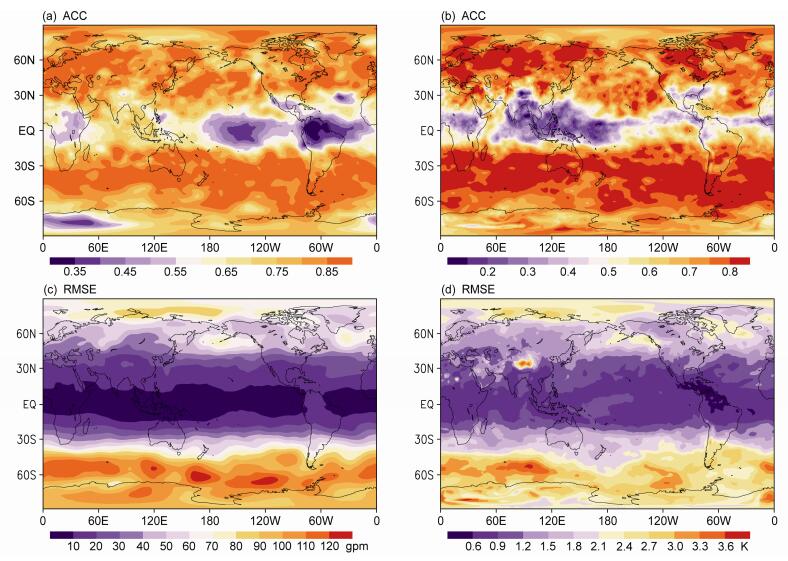
3.2 GRAPES全球模式误差分布图 1为全球范围内1984~2014年逐年7月15~24日的31个个例模式预报第7天的18:00(协调世界时,下同)500 hPa位势高度和温度模式预报场ACC (Anomalous Correlation Coefficient)、RMSE (Root Mean Square Error) 平均空间分布。总体上,位势高度和温度ACC呈现相似的误差分布特点。在中高纬地区流型预报较好,位势高度ACC超过0.8,而热带地区ACC值基本小于0.55,其低值区主要集中在西太平洋,南美洲北部及南极大陆,温度ACC低值区则主要集中在印度洋和西太平洋,体现在ACC小于0.7的区域。青藏高原地区位势高度和温度的ACC都相对较低,说明大地形区域的流型预报质量欠佳,而中高纬度的位势高度和温度场表现都相对较好。而从RMSE平均分布可见,热带地区和北半球位势高度和温度均方根误差较小,在10~30 gpm之间,南半球中高纬、北极区和青藏高原的预报温度和位势高度存在较大的均方根误差。总体而言,GRAPES全球模式预报500 hPa位势高度和温度在中高纬度与再分析资料具有较高的形相似,热带地区形相似较差,但热带区域的温度和位势高度值偏差则较小,南半球中高纬和极地的值偏差较大,南极大陆和青藏高原大地形区域存在偏差大值中心。
|
图 1 1984~2014年7月15~24日500 hPa全球 (a、c) 位势高度、(b、d) 温度的31年模式预报第7天18:00(协调世界时,下同) 模式预报场 (a、b) ACC、(c、d) RMSE平均值的空间分布 Figure 1 Spatial distributions of (a, b) ACC (Anomalous Correlation Coefficient) and (c, d) RMSE (Root Mean Square Error) of 500-hPa (a, c) geopotential height and (b, d) temperature at 1800 UTC of the 7th day of the 10-day prediction (15-24 July) averaged from 1984 to 2014 |
Peng et al.(2013)和和常俊等 (2015)描述了ANO方法的原理。太阳辐射是驱动地球大气运动的根本动力,而太阳高度角是影响太阳辐射能的决定指标。如果不考虑随机过程,太阳相同的高度角时,大气获得相同的能量。大气由于自身复杂动力过程作用和海陆动力、热力等外源的强迫,成为一个高度非线性系统。大气中运动遵循牛顿第二定律、热力学第一定律和连续方程。任一变量s的变化可以概括为
| $ \frac{\partial s}{\partial t}=L(s)+N(s)+\varepsilon $ | (1) |
其中,L(s) 和N(s) 分别表示关于预报变量s的线性和非线性部分,ε代表模式误差。大气变量s在某一时间段上可以分解为气候态s和同时间内的气候态的天气扰动量s′,即:
| $ s=\bar{s}+{s}' $ | (2) |
对公式 (1) 关于时间求平均并结合公式 (2),考虑到线性项
| $ \frac{\partial \bar{s}}{\partial t}=L(\bar{s})+\overline{N(s)}+\bar{\varepsilon } $ | (3) |
从公式 (3) 看出,模式输出的气候与实际的气候之间存在差异,亦表现出系统误差增长的机制,这种差异并非是初值偏差的放大,还有气候部分再分解后的截断误差放大,导致影响数值预报技巧。
由公式 (1) 和 (3) 积分可得天气扰动量:
| $ {s}'=\int{\frac{\partial s}{\partial t}}\text{d}t-\int{\overline{(\frac{\partial s}{\partial t}}})\text{d}t=\int{\frac{\partial s}{\partial t}}\text{d}t-{\sum\limits_{i=1}^{n}{{{\left(\int{\frac{\partial s}{\partial t}\text{d}t} \right)}_{i}}}}/{n}\; $ | (4) |
通过公式 (4) 得到了天气预报场的天气扰动部分。气候场是天气变化的多年平均,对天气预报而言可认为是不变的,因此可以充分利用历史资料,得到大气真实的气候态
| $ {{s}_{p}}={{\bar{s}}_{a}}+{s}' $ | (5) |
用已有的观测资料求得的sa是大气最真实演变的刻画,用其代替模式气候态s可以提高数值预报技巧,消除了模式气候态的误差。利用历史观测资料获得气候场,而天气扰动场则由模式积分预报,从而部分消除了模式气候态系统误差,使预报场sp更加接近真实。此订正方法称为ANO方法。
4.1.2 MOS方法MOS (Model Output Statics) 作为一种线下统计订正方法 (Glahn and Lowry, 1972) 被广泛应用,其原理是直接利用历史数值预报产品的质量评估,与同时期的局地天气要素实测值之间建立统计预报关系,进而利用实时数值预报产品和这种统计关系做出局地天气预报。这种误差订正统计模型,即模式输出统计方法,简称MOS方法。MOS方法中需要确认资料的正确性、调整预报因子及个数,并对统计预报方程不断检验、改进,改善预报质量。本文中根据模式输出的各种气象要素,选取针对500 hPa温度场预报的合适的因子。为可能全面地选取影响因子,首先关注其它要素 (如气压、温度梯度、大气稳定度等) 的影响,并逐步剔除不适因子、优选控制因子数目。建立预报方程后通过添加不同因子检验出其影响系数、筛选出对500 hPa温度最为合适的预报因子,由此确定500 hPa经纬向风场和湿度,200 hPa、500 hPa和700 hPa的位势高度、地面2 m温度和海平面气压等10个物理量作为预报因子。这种方法需要建立预报量与模型其它要素场的线性统计模型,要素选择具有人为因素,且计算量大,还有模型随时间和地点变化的缺点,业务应用中需要有大量的计算资源保证。
4.2 GRAPES全球中期预报的ANO方法要素订正为客观评价模式预报结果的质量,我们采用距平相关系数 (ACC) 和均方根误差 (RMSE) 来评价预报场与再分析 (实况) 场的相似程度。ACC测定两个变量之间线性相关程度,主要描述两个空间变量场间的形状相似程度,而RMSE是衡量空间变量预报值与观测值的偏差大小,二者分别从形和值两个角度描述预报场与观测场的相似性。这里以ERA-interim再分析资料作为实况历史资料使用,时间序列为模拟时段每天4个时次的样本。ACC与RMSE的表达式为
| $ \text{ACC}=\frac{\sum\limits_{i, j}{({{f}_{i, j}}-\bar{f})({{a}_{i, j}}-\bar{a})}}{\sqrt{\sum\limits_{i, j}{{{({{f}_{i, j}}-\bar{f})}^{2}}\sum\limits_{i, j}{{{({{a}_{i, j}}-\bar{a})}^{2}}}}}} $ | (6) |
| $ \text{RMSE}=\sqrt{\frac{\sum\limits_{i, j}{{{({{f}_{i, j}}-{{a}_{i, j}})}^{2}}}}{N}} $ | (7) |
其中,f为预报场,a为分析场,“-”代表空间平均场,i、j为经、纬格点序号,N为每层空间上经纬度总格点数。
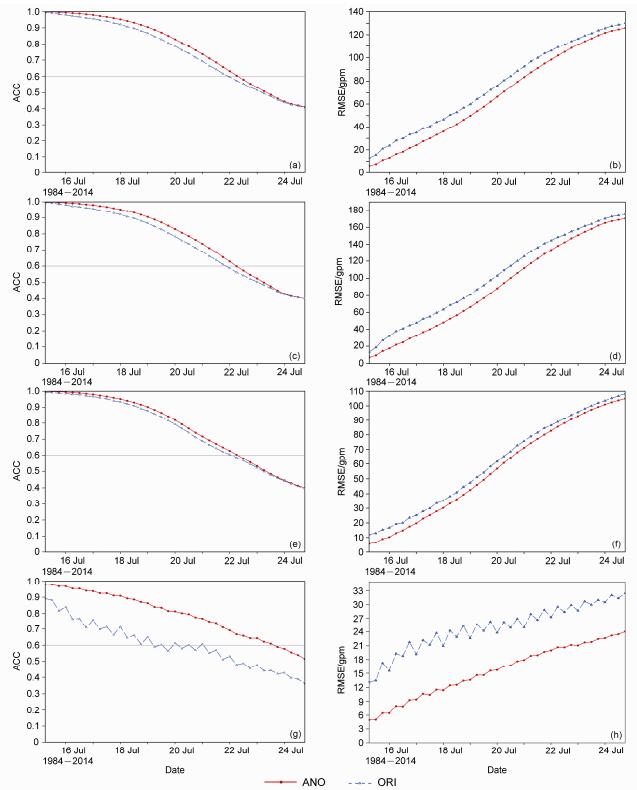
采用GRAPES全球模式对1984~2014年每年7月15~24日相同时段的31个过程进行后报试验。以ERA-interim再分析资料为参考,对模式每日4个时次的输出结果及相应的ANO方法订正结果分别计算ACC和RMSE。200 hPa位势高度的全球 (90°S~90°N)、南半球 (90°S~20°S)、北半球 (20°N~90°N) 和热带地区 (20°S~20°N) 的31个个例平均ACC和RMSE随时间演变情况在图 2中给出。在对流层高层,位势高度的ANO订正预报具有显著效果,无论平均距平相关系数还是均方根误差都有明显改善,200 hPa全球平均ACC大于0.6的日数从原有7.3 d提高到7.7 d,平均RMSE则在7 d预报结果中减小了近10 gpm。相比发现,南半球GRAPES预报结果的订正效果比北半球有更好表现,其中南半球的位势高度平均ACC大于0.6的天数增加了0.6 d,北半球平均约增加0.3 d,RMSE的南、北半球平均分别降低13 gpm和6 gpm,这与南半球观测资料稀少,导致GRAPES模式的预报技巧较低,系统误差较大有关。在热带地区,ANO对预报的改善最为明显,订正的31年平均ACC大于0.6的天数接近9.3 d,较原预报延长了5.8 d,10 d预报的RMSE 31年平均值减小幅度在14~22 gpm之间。在500 hPa、700 hPa和850 hPa位势高度上 (图略),ANO方法的订正效果也非常类似,在热带地区改善最为显著,而北半球较南半球稍差。随着预报时效延长,误差逐渐增大,预报场的形相似和值相似程度降低,而ANO的订正幅度也在7天后明显下降。在垂直方向,对流层中高层环流形势的预报技巧和订正效果都好于低层,即200 hPa效果好于500 hPa和850 hPa,高层到低层ACC大于0.6的天数逐渐减少,但都超过6 d。因此,ANO方法无论在全球范围还是分区的中期预报显示较好的订正效果。
|
图 2 31年 (a、b) 全球、(c、d) 南半球、(e、f) 北半球以及 (g、h) 热带地区的10 d预报200 hPa位势高度平均ACC (左列)、RMSE (右列) 随时间演变。ANO:模式距平积分订正;ORI:原始模式预报 Figure 2 Time series of 31-year averaged ACC (left column) and RMSE (right column) of geopotential height at 200 hPa (a, b) over the globe, (c, d) in the Southern Hemisphere, (e, f) in the Northern Hemisphere, and (g, h) over the tropics by ANO (Anomaly Numerical-correction with Observations) calibration and original predictions (ORI) |
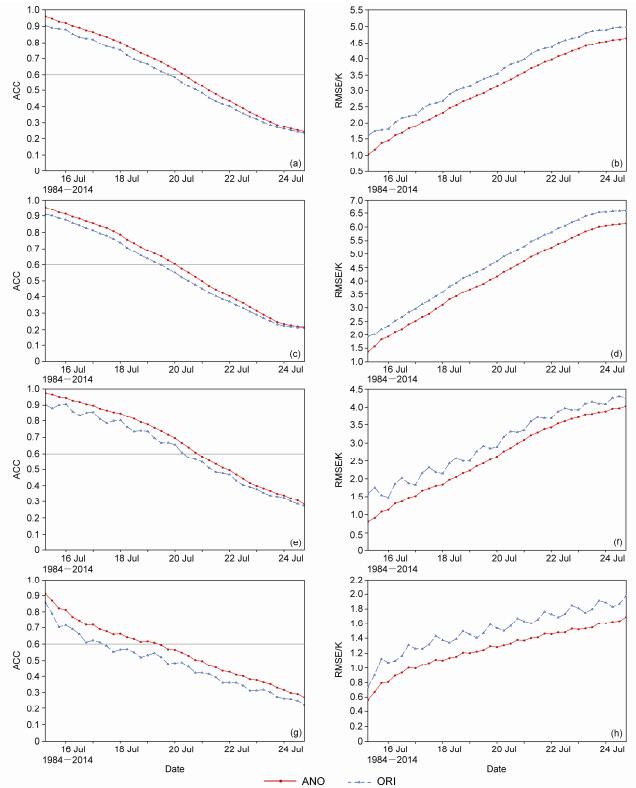
在图 3中我们给出了850 hPa温度场的全球、南半球、北半球和热带地区平均ACC和RMSE的时间演变。全球低层温度场的订正也显示了与位势高度相似的结果,31年平均的一周预报温度场的ACC在订正后提高约0.06,ACC>0.6的有效预报天数平均延长0.5 d。图 3中可见,对于低层温度场,南北半球的ANO订正效果相差不大,但北半球的原模式预报表现出明显的误差日变化特征,而南半球则不明显,这与模式低层大气温度受地面加热影响较大有关,北半球陆面较多,地表温度日变化明显,南半球则多海洋,表面温度日变化较弱。就平均RMSE的演变可见,平均误差随预报时效延长而增加,利用历史资料通过ANO方法订正后温度预报误差平均降低0.6 K,显著提高了GRAPES预报中高纬温度场的预报质量。同时,订正后热带地区ACC有0.1以上的提高,大于0.6的天数在订正后延长了近2 d,而RMSE则降低了0.2~0.4 K。从温度订正预报的垂直分布看,表现出与位势高度相反的变化趋势,低层预报订正效果好于对流层中高层,即850 hPa效果好于500 hPa和200 hPa,也反映出GRAPES模式的温度预报系统误差随高度减小的事实。
对风分量和湿度的订正也显示出明显正效果,但风场改善相对较小。总体而言,ANO方法对于各物理量预报技巧都有改善,其中位势高度场和温度场的订正改进较大,ANO方法可帮助GRAPES全球模式提高中期预报水平。
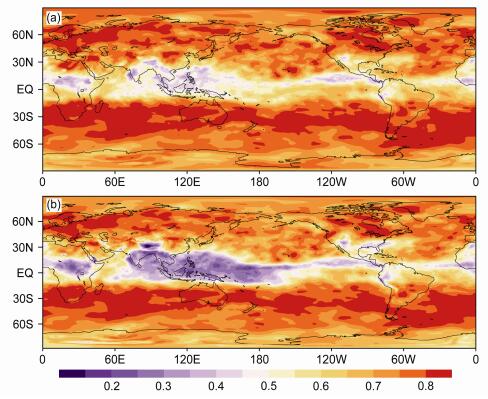
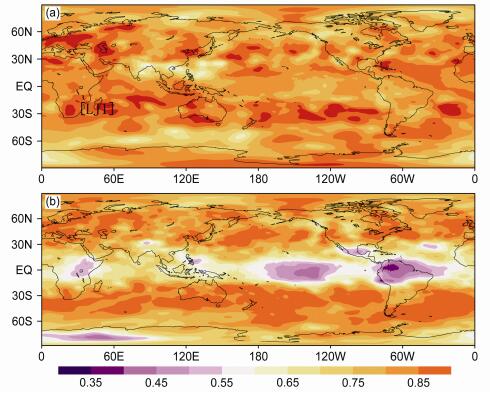
物理量ACC的时变特征反映了天气型预报的变化,通过计算31个个例平均的500 hPa高度场和温度场格点时间序列 (360×180个格点) ACC可以反映整个时间—空间变化和观测结果的一致性。图 4是500 hPa高度场的平均ACC在全球区域的空间分布,可以看出原模式预报 (图 4b) 的ACC呈现出一周预报 (图 1) 相似的结果,北半球及南半球中高纬地区数值相对较大,热带地区则相对较小。在青藏高原、南美洲北部和墨西哥附近出现ACC低值中心,与该地区的复杂地形和模式地形处理有关。在对500 hPa高度场订正之后 (图 4a),南美洲安德斯山、墨西哥附近及极地地区效果显著,模式误差基本被消除,ACC平均提高0.2左右,普遍大于0.6,ACC在0.7以上占据了大部分地区。
|
图 4 1984~2014年500 hPa位势高度10 d预报场ACC平均值空间分布:(a) ANO订正结果;(b) 模式预报 Figure 4 Spatial distributions of ACC of 10-day 500 hPa geopotential height forecasts averaged during 1984-2014: (a) ANO calibration; (b) original predictions |
图 5的500 hPa温度场订正前后的比较也可以看出原预报在热带地区的预报效果欠佳,反映了GRAPES模式在热带的预报温度分布偏差。通过模式系统误差订正,热带地区和极地改善较大,ACC提高,太平洋中部和印度洋体现最为明显,而青藏高原区域ACC平均提高0.1。本文同时也计算了500 hPa水平风场 (图略) 的ACC平均值空间分布,发现风场的订正有正效果,但不及温度场明显。通过以上分析可以看出,ANO对位势高度场和温度场的订正效果显著,可以提高2周内的GRAPES全球数值天气预报技巧。
4.3 ANO与MOS订正结果的对比MOS方法是一种常用的动力统计方法,但计算量较大。受计算条件的限制,本文无法对所有个例进行对比分析。根据Chen and Zhai (2013)对持续性强降水进行了定义和分类,我们选择了1994年7月15~21日江淮持续性降水过程为例,对ANO方法和MOS方法的订正结果进行比较分析,重点把握高空两槽一脊 (乌拉尔山东北侧及雅库茨克的槽、贝加尔湖西北的脊)、偏南偏西的副热带高压、偏南的200 hPa南亚高压和位于高原主体及北侧的西风急流增强等环流要素。本文根据刘还珠等 (2004)和陈豫英等 (2011)选取预报因子建立MOS预报模型,关注上文所提影响该持续性降水天气过程四个关键因素和因子的动态剔除与引进,确定500 h Pa经纬向风场和湿度,200 hPa、500 hPa和700 hPa的位势高度,地面2 m温度和海平面气压等10个物理量作为预报因子,建立预报模型对 (26°~40°N,97°~116°E) 范围的320个格点500 hPa温度场进行预报和订正。
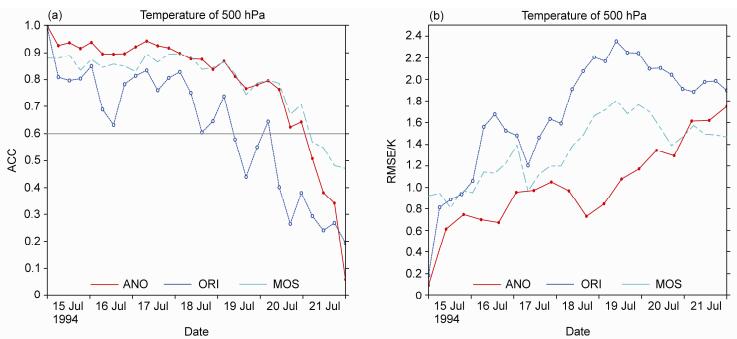
图 6为该个例ANO方法、MOS方法和GRAPES模式预报500 hPa温度场在 (26°~40°N,97°~116°E) 区域内平均的ACC和RMSE随时间演变。可以看出ANO订正与MOS预报结果的ACC和RMSE变化趋势一致,都有明显改善。比较而言,前6天ANO订正效果好于MOS预报,ANO订正后RMSE减小幅度在0.2~1.3 K之间,MOS预报的温度RMSE在0.5 K左右。对于持续性降水天气过程,ANO的订正效果较MOS统计预报为好。同时,本试验中MOS方法计算的终端时间需约5.5 h,为ANO订正方法的320倍,计算耗时多,业务应用面临不小的困难。
|
图 6 1994年7月15~21日500 hPa温度场ANO、MOS (Model Output Statistics)、ORI预报的 (a) ACC和 (b) RMSE时间演变 Figure 6 Time series of (a) ACC and (b) RMSE of 500-hPa temperature from ANO, MOS (Model Output Statistics), and ORI (original predictions) during 15-24 July 1994 |
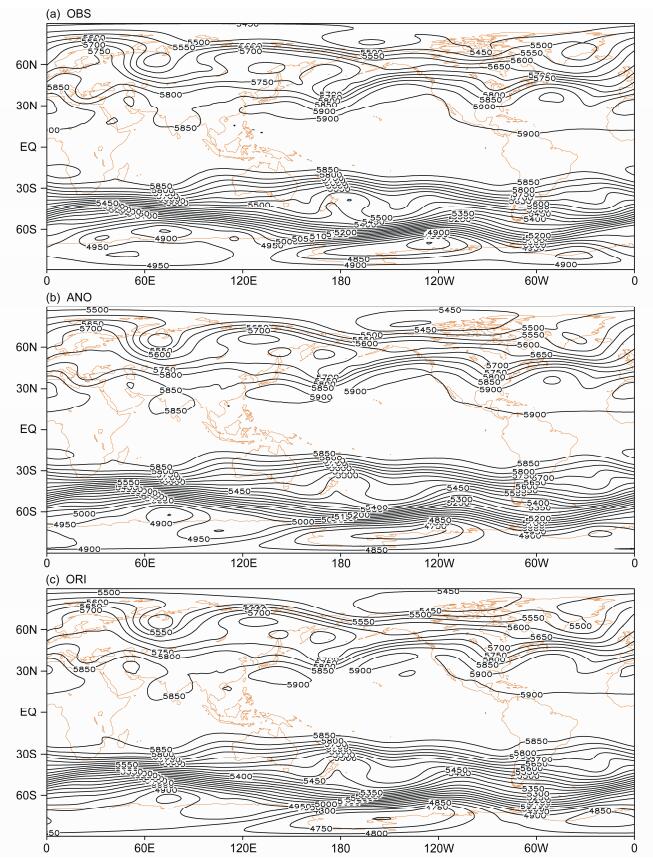
为进一步检验ANO对GRAPES全球预报效果的改善效果,我们进一步给出了2014年7月15~21日的500 hPa全球位势高度预报和订正结果。从图 7a可以看出,北半球进入7月中旬,高纬盛夏的四波环流型明显,有切断低压位于白令海地区;中纬度的西风带活动经向度较高,短波系统更迭频繁;北半球副高系统整体偏强,其中以北美中部至北非副高单体为最强。北美中纬度地区的环流大致为一脊一槽式,北美洲中、西、南部地区受强势的副高控制,脊线在45°N左右,而槽已抵至近赤道地区,由东至西蔓延至东亚40°N位置,触头伸向中国东南沿海城市及台湾东北部,集中活跃在30°N附近;北大西洋40°N以南的地区被副高牢牢掌控,而其北侧的西风带内槽脊振幅颇大:格陵兰上空有低压中心控制,南侧长波槽不断东移;地中海西南部的北非—南欧有副高—南支脊系统控制,而下游的东南欧—黑海地区有一道宽泛南伸的槽位控制,底部直达地中海30°N。在鄂毕河南部南伸大槽向东不断移动,同样贝加尔湖东北方向有一切断低压控制,东移大槽在阿留申急剧南倾,幅度最大;在北半球太平洋上,副高控制了40°N以南的大片洋区。在南半球环流形势分布更加密集,但与北半球相比变化相对平缓,在中太平洋南部有一北突脊出现,其南侧有一低压中心控制在南极洲北侧大部分地区,总体呈现一脊一槽分布。对比图 7b、c,原预报在副高的控制位置及纬度幅度与观测值有不小的偏差,副高单体较多,纬度偏北,在亚洲东部明显西伸但并未触及包括台湾在内的中国大陆地区。格陵兰上的低压减弱并入大槽不断东移。而白令海峡的切断低涡也没有明显预报,在南半球地区,南极北部的低压中心值较低,位置有所偏移,所占纬度不及观测值准确,总体上大体形势趋于一致,又不能相似到具体的系统上。而ANO方法订正之后的环流场更加接近观测值,虽然副高在太平洋有一单体出现,但是强度及幅度较精确,槽脊振幅变化范围一致,由此看出,ANO方法不仅在数值“值相似”上对预报值有改善的作用,在“型相似”上也体现着提高技巧。
|
图 7 2014年7月15~21日500 hPa高度场(等值线,单位:gpm)的环流形势:(a)OBS(实测);(b)ANO;(c)ORI Figure 7 Circulation features of 500-hPa geopotential height (contours, units: gpm) from (a) OBS (observation), and (b) ANO and (c) ORI predictions during 15–21 July 2014 |
采用1984~2014年7月15~24日的31年同一时段ERA-interim再分析资料作为大气实际状态,在分析GRAPES全球非静力模式误差分布的基础上对预报误差进行了为期10天的订正试验,分别采用ANO订正技术和MOS统计预报形成了动力—统计结合的订正预报结果。对31年间7月15~24日同一时段的订正结果统计,显示了ANO方法对GRAPES全球模式预报误差的显著订正效果,改善了模式流型预报并降低了各时间点的预报误差。
分析500 hPa位势高度和温度场ACC、RMSE平均空间分布发现,GRAPES全球模式的预报误差在南极大陆、青藏高原地区表现突出。温度和位势高度场反映的流型预报表现为赤道低纬差、中高纬较好,而均方根误差则表明低纬误差小、中高纬误差大的特点。表明模式预报低纬地区的温压场数值分布接近实况,但系统错位,而中高纬数值误差较大,但系统配置预报较好。
以31个个例中的任意30个表征模式预报气候态,对另1个预报进行ANO订正,我们获得了31个订正预报结果。订正结果对应ERA-interim再分析场在全球、南半球、北半球和热带地区的ACC和RMSE显示,位势高度的ANO订正对改善预报具有显著效果,无论平均距平相关系数还是均方根误差都有明显改善,全球的200 hPa位势高度平均ACC大于0.6的日数从原有7.3 d提高到7.7 d,平均RMSE则在7 d预报中减小了10 gpm。南半球的订正效果比北半球更好,南半球位势高度平均ACC>0.6的天数增加了0.6 d,而北半球增加0.3 d,RMSE在南、北半球平均分别降低13 gpm和6 gpm。在热带地区,ANO对预报的改善最为明显,订正后位势高度31年平均ACC大于0.6的天数接近9.3 d,较原预报延长了5.8 d,31年间的10 d预报订正位势高度RMSE减小幅度在14~22 gpm之间。对于位势高度场,对流层中高层的订正效果好于低层,ACC大于0.6的天数从高层到低层逐渐减少,但都超过6 d。850 hPa温度场的订正也显示,全球31年平均的温度场一周预报结果ACC在订正后提高约0.06,ACC>0.6的有效预报天数平均延长0.5 d。由于陆地分布广泛,北半球预报温度误差表现出明显的日变化特征,而南半球则不明显。就温度平均RMSE的演变可见,误差随预报时效延长而增加,订正后全球温度预报误差平均降低0.6 K,热带地区850 hPa温度ACC有0.1以上的提高,大于0.6的天数延长了近2 d,而RMSE则降低了0.2~0.4 K。从温度订正预报的垂直分布看,低层预报订正效果好于对流层中高层,也反映出GRAPES模式的温度预报系统误差随高度减小的事实。对风分量和湿度的订正也显示出明显正效果,但风场改善相对较小。总体而言,ANO方法对于各物理量预报技巧都有改善,其中位势高度场和温度场的订正改进较大,ANO方法对提高GRAPES全球模式的中期预报水平有帮助。
ANO与常用的MOS方法在青藏高原东麓附近500 hPa温度场订正和预报中进行了比较,以了解ANO方法的效果和实用性。结果发现ANO订正效果和MOS方法的预报结果相近,但在一周内的预报中试验中ANO效果占优。相对MOS方法大量的计算,ANO是一种经济有效的统计预报方法。在实际预报中,订正结果与观测场变化趋势较为一致,各个系统的预报也到达预期结果,体现出“型相似”的改善效果,可以做到更加接近真实观测情况。结合历史资料,运用ANO方法对GRAPES模式预报结果进行订正,有效消减了模式系统误差。对于地面要素场和降水的订正、以及不同季节天气预报的订正试验有待进一步开展,特别是由于降水的不连续性,高分辨数值预报的误差订正试验是必要的。
致谢: 感谢国家数值中心的张红亮和苏勇老师在GRAPES模式使用方面的帮助,感谢评审专家给出的文章结构与内容的修改建议。| [] | 常俊, 彭新东, 范广洲, 等. 2015. 结合历史资料的数值天气预报误差订正[J]. 气象学报, 73(2): 341–354. Chang Jun, Peng Xindong, Fan Guangzhou, et al. 2015. Error calibration of numerical weather prediction with historical data[J]. Acta Meteor. Sinica (in Chinese), 73(2): 341–354, DOI:10.11676/qxxb2015.021. |
| [] | 陈德辉, 薛纪善. 2004. 数值天气预报业务模式现状与展望[J]. 气象学报, 62(5): 623–633. Chen Dehui, Xue Jishan. 2004. An overview on recent progresses of the operational numerical weather prediction models[J]. Acta Meteor. Sinica (in Chinese), 62(5): 623–633, DOI:10.11676/qxxb2004.061. |
| [] | 陈德辉, 沈学顺. 2006. 新一代数值预报系统GRAPES研究进展[J]. 应用气象学报, 17(6): 773–777. Chen Dehui, Shen Xueshun. 2006. Recent progress on GRAPES research and application[J]. J. Appl. Meteor. Sci. (in Chinese), 17(6): 773–777, DOI:10.3969/j.issn.1001-7313.2006.06.014. |
| [] | 陈德辉, 薛纪善, 杨学胜, 等. 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J]. 科学通报, 53(22): 3433–3445. Chen Dehui, Xue Jishan, Yang Xuesheng, et al. 2008. New generation of multi-scale NWP system (GRAPES):General scientific design[J]. Chinese Science Bulletin, 53(22): 3433–3445, DOI:10.1007/s11434-008-0494-z. |
| [] | Chen Y, Zhai P M. 2013. Persistent extreme precipitation events in China during 1951-2010[J]. Climate Res., 57(2): 143–155, DOI:10.3354/cr01171. |
| [] | 陈豫英, 陈楠, 王素艳, 等. 2011. MOS方法在动力延伸期候平均气温预报中的应用[J]. 应用气象学报, 22(1): 86–95. Chen Yuying, Chen Nan, Wang Suyan, et al. 2011. Application of MOS method on pentad mean temperature prediction in dynamical extended range[J]. J. Appl. Meteor. Sci. (in Chinese), 22(1): 86–95, DOI:10.3969/j.issn.1001-7313.2011.01.009. |
| [] | 丑纪范. 1986. 为什么要动力-统计相结合?——兼论如何结合[J]. 高原气象, 5(4): 367–372. Chou Jifan. 1986. Why we need and how to combine the dynamic with statistic methods?-How to combine?[J]. Plateau Meteor. (in Chinese), 5(4): 367–372. |
| [] | 丑纪范. 2007. 数值天气预报的创新之路——从初值问题到反问题[J]. 气象学报, 65(5): 673–682. Chou Jifan. 2007. An innovation road to numerical weather prediction-From initial value problem to inverse problem[J]. Acta Meteor. Sinica (in Chinese), 65(5): 673–682, DOI:10.11676/qxxb2007.061. |
| [] | 丑纪范, 任宏利. 2006. 数值天气预报——另类途径的必要性和可行性[J]. 应用气象学报, 17(2): 240–244. Chou Jifan, Ren Hongli. 2006. Numerical weather prediction-Necessity and feasibility of an alternative methodology[J]. J. Appl. Meteor. Sci. (in Chinese), 17(2): 240–244, DOI:10.3969/j.issn.1001-7313.2006.02.015. |
| [] | 达朝究. 2011. 一个可能提高GRAPES模式业务预报能力的方案[D]. 兰州大学博士学位论文. Da Chaojiu. 2011. One scheme which maybe improve the forecasting ability of the global (regional) assimilation and prediction system[D]. Ph. D. dissertation (in Chinese), Lanzhou University. |
| [] | Glahn H R, Lowry D A. 1972. The use of Model Output Statistics (MOS) in objective weather forecasting[J]. J. Appl. Meteor., 11(8): 1203–1211, DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2. |
| [] | 顾震潮. 1958. 天气数值预报中过去资料的使用问题[J]. 气象学报, 29(3): 176–184. Gu Zhenchao. 1958. On the utilization of past data in numerical weather forecasting[J]. Acta Meteor. Sinica (in Chinese), 29(3): 176–184, DOI:10.11676/qxxb1958.019. |
| [] | Huang J P, Yi Y H, Wang S W, et al. 1993. An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution[J]. Quart. J. Roy. Meteor. Soc., 119(511): 547–565, DOI:10.1002/qj.49711951111. |
| [] | Li X H, Peng X D, Li X L. 2015. An improved dynamic core for a non-hydrostatic model system on the Yin-Yang grid[J]. Adv. Atmos. Sci., 32(5): 648–658, DOI:10.1007/s00376-014-4120-5. |
| [] | 刘还珠, 赵声蓉, 陆志善, 等. 2004. 国家气象中心气象要素的客观预报——MOS系统[J]. 应用气象学报, 15(2): 181–191. Liu Huanzhu, Zhao Shengrong, Lu Zhishan, et al. 2004. Objective element forecasts at NMC-A MOS system[J]. J. Appl. Meteor. Sci. (in Chinese), 15(2): 181–191, DOI:10.3969/j.issn.1001-7313.2004.02.006. |
| [] | Peng X D, Che Y Z, Chang J. 2013. A novel approach to improve numerical weather prediction skills by using anomaly integration and historical data[J]. J. Geophys. Res., 118(16): 8814–8826, DOI:10.1002/jgrd.50682. |
| [] | 钱维宏. 2012. 如何提高天气预报和气候预测的技巧?[J]. 地球物理学报, 55(5): 1532–1540. Qiang Weihong. 2012. How to improve the skills of weather and climate predictions?[J]. Chinese J. Geophys. (in Chinese), 55(5): 1532–1540, DOI:10.6038/j.issn.0001-5733.2012.05.010. |
| [] | 邱崇践, 丑纪范. 1990. 预报模式的参数优化方法[J]. 中国科学 (B辑), 20(2): 218–224. Qiu Chongjian, Chou Jifan. 1990. Parameter optimization method of prediction model[J]. Science China (B), 20(2): 218–224, DOI:10.1360/zb1990-20-2-218. |
| [] | 任宏利, 丑纪范. 2005. 统计-动力相结合的相似误差订正法[J]. 气象学报, 63(6): 988–993. Ren Hongli, Chou Jifan. 2005. Analogue correction method of errors by combining both statistical and dynamical methods together[J]. Acta Meteor. Sinica (in Chinese), 63(6): 988–993, DOI:10.11676/qxxb2005.094. |
| [] | 徐国强, 杨学胜, 黄丽萍, 等. 2010. GRAPES中地形重力波拖曳物理过程的引进和应用试验[J]. 气象学报, 68(5): 631–639. Xu Guoqiang, Yang Xuesheng, Huang Liping, et al. 2010. Introducing and application testing of the orographic gravity wave drag parameterization physics in the GRAPES[J]. Acta Meteor. Sinica (in Chinese), 68(5): 631–639, DOI:10.11676/qxxb2010.062. |
| [] | 杨学胜, 沈元芳, 徐国强. 2009. 辐射方案对GRAPES全球模式的影响[J]. 大气科学, 33(3): 593–599. Yang Xuesheng, Shen Yuanfang, Xu Guoqiang, et al. 2009. The impacts of radiation schemes on the GRAPES global model[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 33(3): 593–599, DOI:10.3878/j.issn.1006-9895.2009.03.16. |
| [] | 翟盘茂, 倪允琪, 陈阳. 2013. 我国持续性重大天气异常成因与预报方法研究回顾与未来展望[J]. 地球科学进展, 28(11): 1177–1188. Zhai Panmao, Ni Yunqi, Chen Yang. 2013. Mechanism and forecasting method of persistent extreme weather events:Review and prospect[J]. Advances in Earth Science (in Chinese), 28(11): 1177–1188, DOI:10.11867/j.issn.1001-8166.2013.11.1177. |
| [] | 张人禾, 沈学顺. 2008. 中国国家级新一代业务数值预报系统GRAPES的发展[J]. 科学通报, 53(22): 3429–3432. Zhang Renhe, Shen Xueshun. 2008. On the development of the GRAPES-A new generation of the national operational NWP system in China[J]. Chinese Science Bulletin, 53(22): 3429–3432, DOI:10.1007/s11434-008-0462-7. |
| [] | 庄照荣, 薛纪善, 李兴良, 等. 2010. GRAPES全球模式的模式误差估计[J]. 大气科学, 34(3): 591–598. Zhuang Zhaorong, Xue Jishan, Li Xingliang, et al. 2010. Estimation of model error for the global GRAPES model[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 34(3): 591–598, DOI:10.3878/j.issn.1006-9895.2010.03.11. |
 2017, Vol. 41
2017, Vol. 41