高原低涡、切变线是青藏高原特殊地形条件下形成的典型天气系统,他们主要出现在海拔高度较高和地形坡度陡峭的地区,高原加热和陡峭地形的动力作用可能是低涡、切变线形成的原因之一(徐国昌,1984;Shen et al., 1986;何光碧等,2009a;李国平等,2016;刘云丰和李国平,2016)。低涡、切变线经常相伴或相继出现,对高原及其以东天气产生重要影响(叶笃正等,1957; 叶笃正和高由禧,1979;姚秀萍等,2014)。高原横切变线多出现在32.5°N附近,高频中心在西藏那曲,竖切变线在高原东侧陡坡地区(103°E附近)和高原中部分别有两条高频带(何光碧,2013)。叶笃正和高由禧(1979)早就指出,高原主体上低涡活动最频繁地区与夏季高原准定常的横切变线位置重合。高原低涡和高原切变线既是相互独立的系统,又存在相互影响和相伴相随的过程。马林等(2003)对青藏高原东部牧区成灾性降雪过程进行了较为详细的分析,重点分析了通常情况下高原切变线对高原低涡发生发展所起的主要作用,指出高原切变线西南段为上升运动区且气流的气旋性涡旋处于发展阶段,切变线东北段为下沉运动区且气流的反气旋性涡旋处于发展阶段,是低涡形成的前期条件。Chen and Luo(2003)对东移低涡的动力学研究表明,正涡度场切变基流与低涡的相互作用以及涡流与低涡的合并,是东移低涡强度得以维持和发展的一个直接原因,而高原切变线正是提供了有利的正涡度环境场条件。关于高原切变线的生成机制目前已有一些研究。由天气分析与模型实验表明,在高原北部容易产生高压,此高压南侧的偏东风与高压南部的西南风之间易形成切变线。这些高压有一部分是由伊朗高压东移造成的,但还有不少显然是西风绕过高原北侧时在地形边界层中产生的动力性反气旋环流。从环流变化角度讨论高原切变线成因可能有两种解释(王中和陈艳英,2007):一是西风槽在东移过程中,南段受高原地形及500 hPa西太平洋副热带高压(简称西太副高)的阻挡作用,移动缓慢,从而在高原东部形成东北—西南或东—西向的切变线;二是新疆地区有高压东移与西太副高西北侧的西南气流之间形成一条东北—西南向的切变线。
综上所述,高原切变线与高原低涡都是高原及周边地区重要的灾害天气系统,两者往往伴随出现并且协同产生重要天气影响,但两者间关系的理论观点分歧较大,一种观点认为高原切变线可以激发或诱发高原低涡(先线后涡)(马林等,2003;屠妮妮和何光碧,2010),而另一种观点却认为高原低涡是高原切变线形成的基础(先涡后线)(罗四维,1992;高守亭和周玉淑,2001),并且两者相互作用机理尚不清楚。因此,进一步加强高原低涡与高原切变线之间相互作用的研究具有十分重要的意义。本文通过对一次高原低涡减弱、高原切变线生成的天气系统演变过程与机理探讨,期望加深对高原低涡与高原切变线之间相互作用以及高原切变线生成机理的认识。
2 高原低涡与高原切变线的相关定义高原低涡是指500 hPa等压面上高原地区形成闭合等高线的低压或有3个站点风向呈气旋性的低涡环流(李江萍等,2012;李国平等,2014)。高原切变线是指生成于高原地区,500 hPa等压面上温度梯度小,3个测站风向对吹或2个测站风向对吹且长度大于5个经(纬)距的辐合线。高原低涡与高原切变线之间具有密切联系,高原低涡常在高原中西部生成,然后沿高原切变线或辐合带东移发展,一般在高原的东部减弱消失。高原地区强降水以及高原以东强降水通常是高原低涡与切变线共同作用的结果,人们也常称这样的天气系统组合为“低涡切变”。若高原低涡与高原切变线伴随出现,则为了便于分析“低涡切变”的演变过程,采用以下定义:如果切变线是准静止的,而低涡主要沿着切变线方向移动,这时以切变线的生消或演变来划分过程;如果切变线(或它的大部分)是随着低涡移动的,这时以低涡的演变为主来划分过程(青藏高原气象科学研究拉萨会战组,1981)。
3 高原低涡、切变线过程的天气分析及再分析资料验证由此次过程的天气实况图(图 1)可以看出,2014年8月25日08时(图 1a,北京时,下同),500 hPa环流场上亚欧大陆中高纬度为“两槽两脊”型,贝加尔湖有一个深厚的低压槽,青藏高原(以下简称高原)西北侧为一长波脊,高原西北部有一高压,高原南侧为南支槽,南支槽在其南侧高压的作用下北移靠近高原;高原上有小槽东移,西太副高588 dagpm脊线位于25°N附近,在青海西南部500 hPa高空风场上可以看出有明显的三站风向呈气旋性环流的高原低涡,在高原低涡的东北方有一弱切变线存在,由以上定义可知弱切变线是随着低涡东移的,故以低涡的演变为主进行分析。25日20时(图 2a),高原西北侧的长波脊较上一时刻略向东移,高原西北部的高压加强东伸,高原上的小槽已经移出到高原东北侧,西太副高加强北移。此时,高原低涡减弱,高原切变线生成,在高原上的高压、南支槽和西太副高的共同作用下,青海玉树—安多一带形成的高原横切变线得以维持。26日08时,高原切变线往东南方移向四川。26日20时,高原切变线横跨整个四川中部,强度也达到最强。27日20时,西太副高588 dagpm脊线北跳到27°N以北,并且脊点西伸与东移的高原500 hPa高压合并,使得切变线趋于消失,本次过程结束。
|
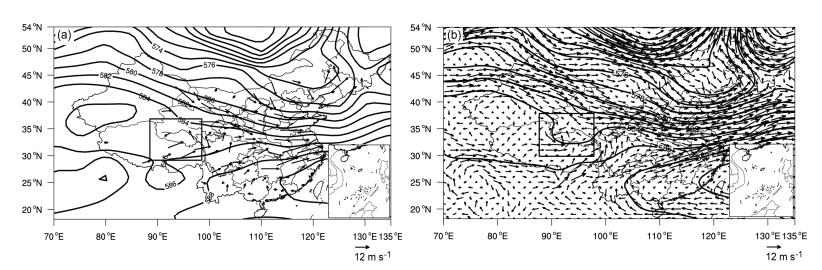
图 1 2014年8月25日08时(北京时,下同)500 hPa位势高度场(等值线,单位:dagpm)和水平风场(箭头,单位:m s-1,黑色框为高原低涡关键区):(a)实况资料;(b)NCEP FNL再分析资料 Figure 1 The geopotential height (contours, units: dagpm) and horizontal wind (arrows, units: m s-1, black rectangles indicate the key region of the plateau vortex) at 500 hPa at 0800 BJT (Beijing time) on 25 August 2014: (a) Observations; (b) NCEP FNL (final) reanalysis data |
|
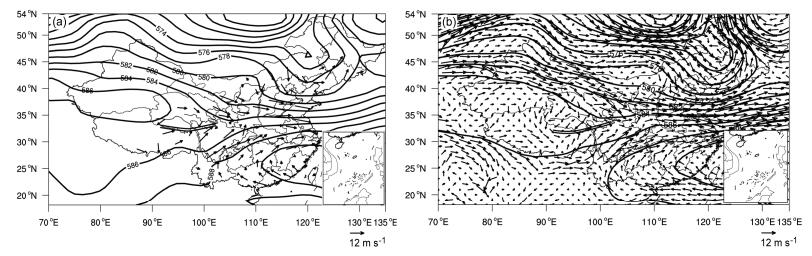
图 2 2014年8月25日20时500 hPa位势高度场(等值线,单位:dagpm)和水平风场(箭头,单位:m s-1,双实线为高原切变线,下同):(a)实况资料;(b)NCEP FNL再分析资料 Figure 2 The geopotential height (contours, units: dagpm) and horizontal wind (arrows, units: m s-1, double solid lines indicate the shear line of the plateau, the same hereafter) at 500 hPa at 2000 BJT on 25 August 2014: (a) Observations; (b) NCEP FNL reanalysis data |
通过对比实况资料和NCEP FNL高分辨率(1°×1°)再分析资料的高度场和风场(图 1、2),可以看出再分析资料能够很好地反映实际的高度场和风场特征。2014年8月25日08时,图 1a方框内为高原低涡关键区,500 hPa高空实测风场可以看出有一明显的气旋性环流,对应于FNL再分析资料的相同区域也有一气旋性环流存在(图 1b)。但是,再分析资料在高原上小槽的强度明显比实况偏强,这可能与高原上的测站偏少有关。25日20时(图 2),从500 hPa高空实测风场和再分析资料风场都可以看到有明显的高原切变线存在,并且切变线的位置较为一致。
为了便于研究,我们把此次过程划分为三个阶段来进行研究,分别为:高原低涡减弱、高原切变线生成即切变线生成阶段(2014年8月25日08时至25日20时)、高原切变线强降水阶段(25日20时至27日08时)和切变线减弱消亡阶段(27日08时至27日20时)。
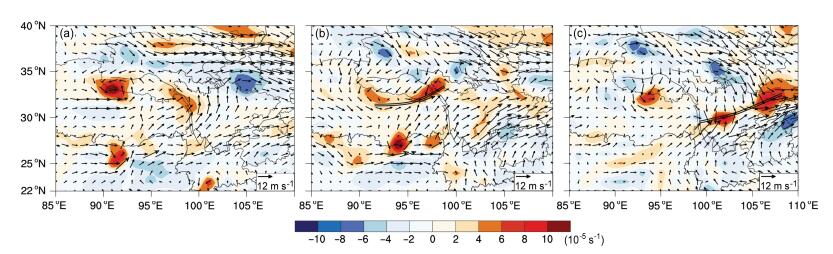
4 高原低涡、切变线过程的涡度和Okubo-Weiss参数特征从整个过程500 hPa涡度场的水平分布可以看出,高原低涡时刻(图 3a),青海西南部有一个明显的气旋性低涡环流,环流中心为正涡度大值中心,中心强度值超过了1.2×10-4 s-1,此时的高原低涡强度较强;高原切变线生成时刻(图 3b),水平风场上气旋性低涡环流消失,正涡度区呈带状分布;高原切变线强降水时刻(图 3c),可以看到青海南部生成的高原切变线已东南移到四川中部,此时的正涡度区仍呈带状分布,东西两端各有一个涡度大值中心。
|
图 3 高原低涡、切变线过程中不同时刻500 hPa相对涡度(阴影,单位:10-5 s-1)和水平风矢量(箭头,单位:m s-1)的变化:(a)高原低涡时刻(8月25日08时);(b)高原切变线生成时刻(8月25日20时);(c)高原切变线强降水时刻(8月26日20时) Figure 3 Relative vorticity (shaded, units: 10-5 s-1) and horizontal wind vectors (arrows, units: m s-1) at 500 hPa at different times during the plateau vortex and shear line process: (a) Occurrence time of the plateau vortex (at 0800 BJT on 25 August); (b) plateau shear line forming time (at 2000 BJT on 25 August); (c) time of heavy rain caused by the plateau shear line (at 2000 BJT on 26 August) |
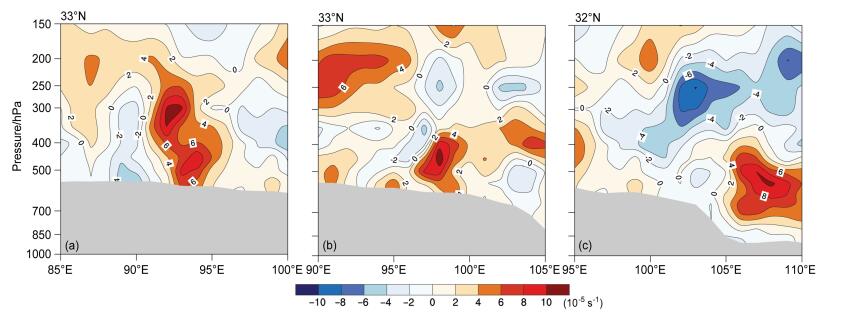
对东移型高原低涡的研究指出,高原低涡在东移过程中,垂直方向上几乎都是正涡度(柳草等,2009)。从不同时刻高原低涡、切变线过程沿涡度大值中心的垂直剖面图可以看出,高原低涡时刻(图 4a),在低涡位置垂直方向上几乎都是正涡度且较强,有助于高原低涡的东移。正涡度中心分布在500~400 hPa之间;高原切变线生成时刻(图 4b),正涡度中心仍然分布在500~400 hPa之间,但强度较上一时刻(即高原低涡时刻)有所减弱。在正涡度中心的上方(对流层高层)出现了负涡度中心,涡度的这种配置有利于产生大气抽吸效应从而有利于降水出现;高原切变线强降水时刻(图 4c),切变线已经移到了四川盆地,正涡度中心在500 hPa达到最强,对流层高层为负涡度中心,有利于降水加强。总的来看,不管是高原低涡还是高原切变线,500 hPa上涡度结构的综合特征比较明显,因此我们选取500 hPa作为本研究天气系统的代表层次,这也符合对高原低涡的一般性认知(刘晓冉和李国平,2006; 高守亭等,2013)。
|
图 4 高原低涡、切变线过程中不同时刻相对涡度(彩色阴影,单位:10-5 s-1)沿其大值中心(各图左上角标注的是系统中心所在纬度)的气压—经度剖面(图底灰色阴影为地形,下同):(a)高原低涡时刻(8月25日08时);(b)高原切变线生成时刻(8月25日20时);(c)高原切变线强降水时刻(8月26日20时) Figure 4 Pressure-longitude cross sections along the center of relative vorticity (colored shadings, units: 10-5 s-1, the central latitude of the system has been labeled in the top left of each figure) at different times during plateau vortex and shear line process (gray shadow at the bottom of the figure indicates topography, the same hereafter): (a) Occurrence time of plateau vortex (at 0800 BJT on 25 August); (b) plateau shear line forming time (at 2000 BJT on 25 August); (c) time of heavy rain caused by plateau shear line (at 2000 BJT on 26 August) |
Dunkerton et al.(2009)和Tory et al.(2013)研究发现,热带气旋总是生成在一个低变形而强旋转的正涡度区域中。借鉴热带气旋的研究成果,本文利用Okubo-Weiss(OW)参数(VOW)来定量表达气流旋转和变形的相对大小。该参数的计算公式如下:
| ${{V}_{\text{OW}}}={{\zeta }^{2}}-(D_{\text{s}}^{2}+D_{\text{t}}^{2})\text{ },$ | (1) |
| $\zeta =\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\text{ },$ | (2) |
| ${{D}_{\text{t}}}=\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\text{ },$ | (3) |
| ${{D}_{\text{s}}}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\text{ },$ | (4) |
其中,ζ为相对涡度(矢量)的垂直分量(简称涡度),Dt为伸缩变形(简称伸缩),Ds为切变变形(简称切变)。OW参数为相对涡度的平方减去这两项变形项的平方,表示气流中相对涡度和变形的相对大小,能够定量描述气流中的旋转和变形程度。当VOW为负值时,表示气流由变形主导,有利于切变线的生成和维持。当VOW为正值时,表示气流以旋转为主,有利于切变线上气旋性涡度的发生、发展,正VOW值越大,表示气流的旋转性越强。
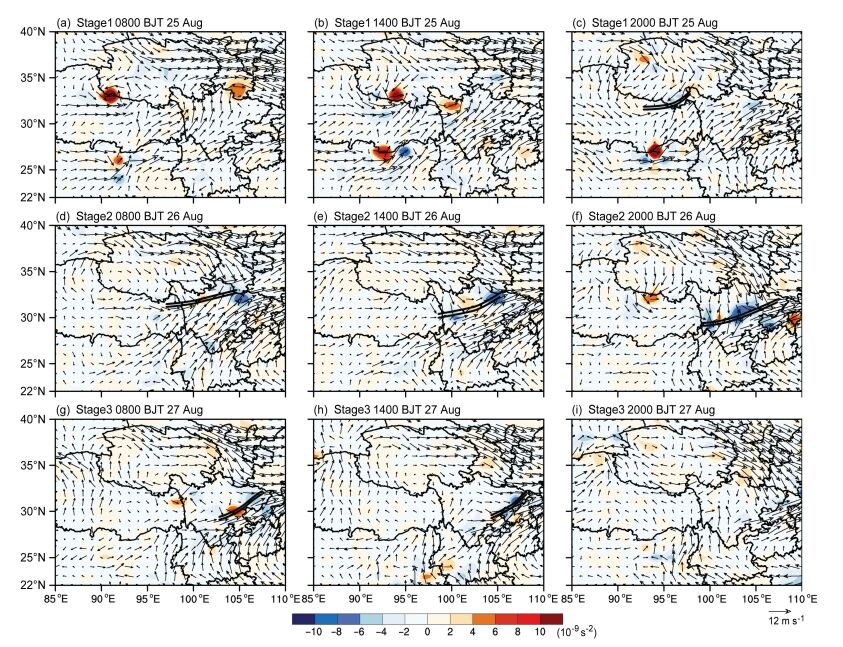
本文通过计算500 hPa上VOW值的大小,来确定高原低涡减弱、高原切变线生成的演变过程以及高原切变线的潜在生成区域和发展状况。由图 5可以清楚地看到,在高原切变线生成阶段(Stage1),2014年8月25日08时(图 5a)青海西南部有一个较强的高原低涡向东移动,此时在高原低涡的位置上VOW值为正值,中心强度为2.29×10-8 s-2。8月25日14时(图 5b)在低涡的位置上VOW仍为正值,但中心强度减弱为1.76×10-8 s-2,说明在低涡位置上气流以旋转为主,但在东移过程中旋转程度有减弱趋势。当高原低涡移到青海、西藏和四川的交界(图 5c),VOW变为负值,中心强度为-5.0×10-9 s-2,并且呈东北—西南向带状分布,说明在这个区域以变形为主,是高原切变线的潜在生成区;在高原切变线强降水阶段(Stage2),切变线上以VOW负值为主,但也存在正值中心,说明在切变线形成后其上仍存在气旋性涡度。VOW负值强度与高原切变线强度有很好的相关性,高原切变线越强时,VOW负值越小。所以,用VOW负值的大小可以很好地指示高原切变线的发展状况;在高原切变线减弱、消亡阶段(Stage3),VOW负值的大小也随之减弱。27日20时,随着高原切变线的消亡,VOW负值中心也基本消失。
|
图 5 2014年8月25~27日500 hPa高原低涡、切变线过程中OW参数(阴影,单位:10-9 s-2)和水平风矢量(箭头,单位:m s-1)的时间演变:切变线生成阶段(Stage1):(a)25日08时,(b)25日14时,(c)25日20时;切变线强降水阶段(Stage2):(d)26日08时,(e)26日14时,(f)26日20时;切变线减弱消亡阶段(Stage3):(g)27日08时,(h)27日14时,(i)27日20时 Figure 5 Temporal evolution of 500-hPa OW (Okubo-Weiss) parameter (shaded, units: 10-9 s-2) and horizontal wind vectors (arrows, units: m s-1) during plateau vortex and shear line process during the period of 25-27 August 2014: Forming stage (Stage1): (a) 0800 BJT on 25 August, (b) 1400 BJT on 25 August, (c) 2000 BJT on 25 August; heavy rain stage (Stage2): (d) 0800 BJT on 26 August, (e) 1400 BJT on 26 August, (f) 2000 BJT on 26 August; weakening and disappearance stage (Stage3): (g) 0800 BJT on 27 August, (h) 1400 BJT on 27 August, (i) 2000 BJT on 27 August |
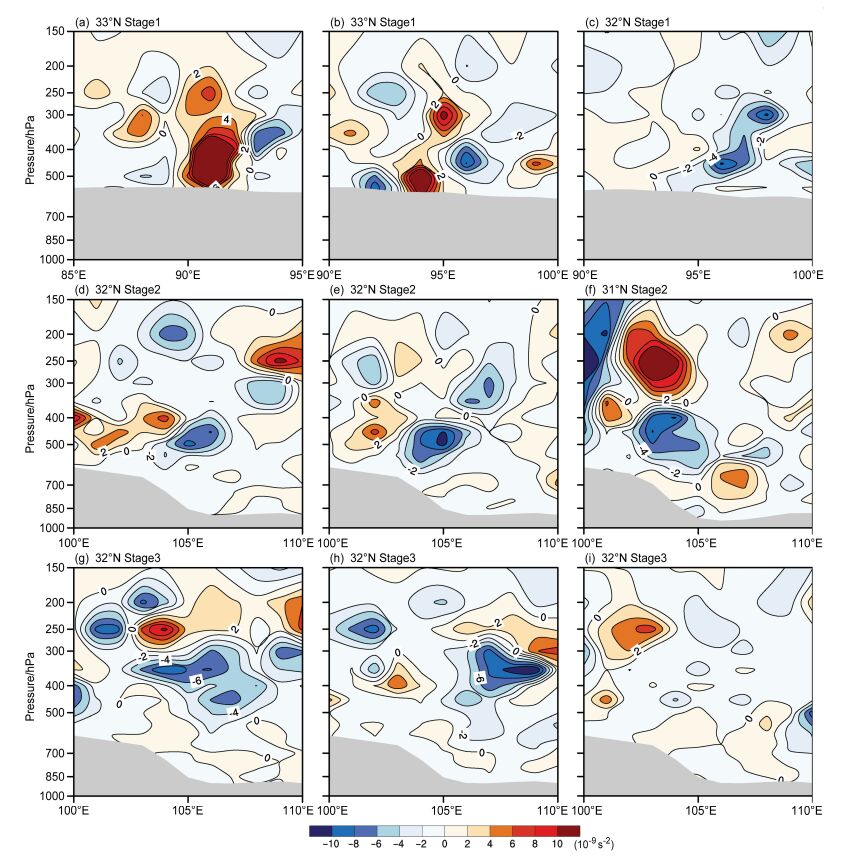
为进一步揭示高原低涡、切变线过程中垂直方向上OW参数的演变状况,从沿OW参数大值中心的气压—经度垂直剖面图(图 6)可见,在高原切变线生成阶段(Stage1),25日08时(图 6a)高原低涡位置上存在正VOW中心,正值中心从近地面层一直向上延伸到300 hPa附近,说明此时旋转性较强,高原低涡强度也较强。25日14时(图 6b),在高原低涡的位置上仍存在VOW正值中心,但强度较上一时刻明显减弱,正值中心的伸展高度也明显降低,其伸展高度从近地面层到500 hPa附近。值得注意的是,近地面层VOW正值中心的上方偏东位置在500~400 hPa之间仍有VOW负值中心存在,这可能表明在东移高原低涡前方的对流层中层(500~400 hPa)变形气流最先发展起来。8月25日20时(图 6c),在高原切变线的生成位置上方存在明显的VOW负值中心,负值中心从近地面层一直伸展到200 hPa,负值中心随高度向东倾斜,说明对流层整层气流以变形为主,有利于高原切变线的形成;在高原切变线强降水阶段(Stage2),500 hPa上存在VOW负值中心,切变线在500 hPa上发展最强。VOW负值中心的上方(200 hPa附近)有VOW正值中心相对应,对流层顶存在反气旋式涡度(图 4c),气流辐散流出,有利于整层上升运动的加强,从而有利于产生强降水;在高原切变线减弱消亡阶段(Stage3),VOW负值中心向高层移动,500 hPa上的VOW负值大小明显减弱。27日20时,VOW负值中心在高原切变线的影响区域基本趋于减弱消失,气流中的变形分量大幅消减,高原切变线也随之减弱消失。
|
图 6 2014年8月25~27日高原低涡、切变线过程中OW参数(阴影,单位:10-9 s-2)沿其大值中心(各图左上角标注的是中心所在纬度)气压—经度剖面的时间演变:切变线生成阶段(Stage1):(a)25日08时,(b)25日14时,(c)25日20时;切变线强降水阶段(Stage2):(d)26日08时,(e)26日14时,(f)26日20时;切变线减弱消亡阶段(Stage3):(g)27日08时,(h)27日14时,(i)27日20时 Figure 6 Temporal evolution of pressure-longitude cross sections along the center of OW parameter (shaded, units: 10-9 s-2, the central latitude has been labeled in the top left of each figure) during the period of 25-27 August 2014: Forming stage (Stage1): (a) 0800 BJT on 25 August, (b) 1400 BJT on 25 August, (c) 2000 BJT on 25 August; heavy rain stage (Stage2): (d) 0800 BJT on 26 August, (e) 1400 BJT on 26 August, (f) 2000 BJT on 26 August; weakening and disappearance stage (Stage3): (g) 0800 BJT on 27 August, (h) 1400 BJT on 27 August, (i) 2000 BJT on 27 August |
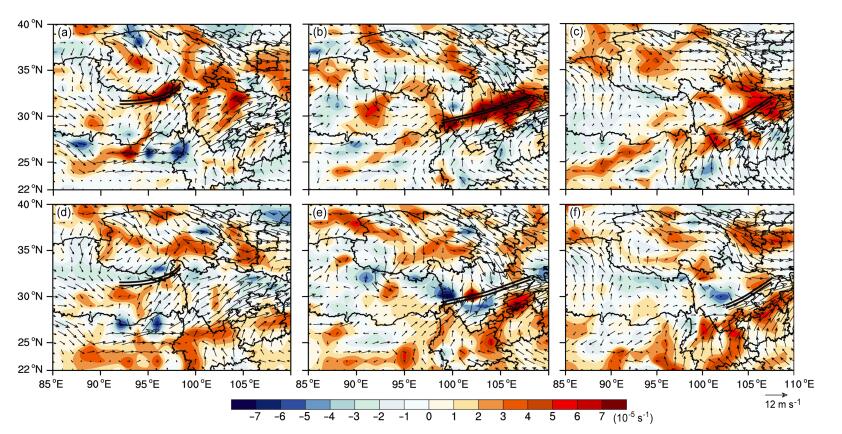
本文应用OW参数定量表达气流旋转和变形的相对大小,变形包括伸缩和切变。但是,不同的高原切变线过程,往往会表现出不同的伸缩、切变变化,如切变为主、伸缩为主、或两者相当等情形。由图 7可以看出,8月25日20时即高原切变线生成时刻,在高原切变线上有较强的伸缩存在,并且伸缩大值中心与高原切变线的走向较为一致。而高原切变线上的切变强度较弱。8月26日20时即高原切变线发展最强时刻,高原切变线上的伸缩大值中心也达到最强,并且沿切变线分布。高原切变线西南段有一个切变正值中心,这与高原切变线上的气旋性涡度有关,高原切变线东北段切变较弱。8月27日08时即高原切变线减弱时刻,高原切变线上的伸缩强度较前两时刻明显减弱,切变也减弱。综上来看,此个例高原切变线以伸缩变形为主。
|
图 7 高原切变线上伸缩和切变的时间演变。伸缩(阴影,单位:10-5 s-1):(a)25日20时,(b)26日20时,(c)27日08时;切变(阴影,单位:10-5 s-1):(d)25日20时,(e)26日20时,(f)27日08时 Figure 7 Temporal evolution of stretching and shearing deformations. Stretching deformation (shaded, units: 10-5 s-1): (a) 2000 BJT on 25 August, (b) 2000 BJT on 26 August, (c) 0800 BJT on 27 August; shearing deformation (shaded, units: 10-5 s-1): (d) 2000 BJT on 25 August, (e) 2000 BJT on 26 August, (f) 0800 BJT on 27August |
Petterssen(1956)将水平风场(u, v)作泰勒级数展开并取近似后可得
| $u\approx {{u}_{0}}+\frac{1}{2}(\delta +{{D}_{\text{t}}})x+\frac{1}{2}({{D}_{\text{s}}}-\zeta )y\text{ },$ | (5) |
| $v\approx {{v}_{0}}+\frac{1}{2}({{D}_{\text{s}}}+\zeta )x+\frac{1}{2}(\delta -{{D}_{\text{t}}})y\text{ },$ | (6) |
其中,(u0, v0)是坐标原点处的风速分量。
| $\delta =\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\text{ ,}$ | (7) |
为水平散度(简称散度)。总变形定义为
| $D=\sqrt{D_{\text{s}}^{2}+D_{\text{t}}^{2}}\text{ }.$ | (8) |
忽略摩擦作用,则等压面上大气运动方程组为
| $\frac{\partial u}{\partial t}+\mathit{\boldsymbol{V}}\cdot \nabla u=fv-g\frac{\partial z}{\partial x}\rm{ },$ | (9) |
| $\frac{\partial v}{\partial t}+\mathit{\boldsymbol{V}}\cdot \nabla v=-fu-g\frac{\partial z}{\partial y}\rm{ },$ | (10) |
其中,V = (u, v, ω)为三维速度矢量,z为位势高度,g为重力加速度,f为科里奥利参数。由公式(10)对x求偏导,公式(9)对y求偏导,二者相减可得到涡度方程:
| $A={{A}_{1}}+{{A}_{2}}+{{A}_{3}}+{{A}_{4}}+{{A}_{5}}\text{ },$ | (11) |
其中,
| $A=\frac{\partial \zeta }{\partial t}\text{ },$ | (12) |
| ${{A}_{1}}=-u\frac{\partial \zeta }{\partial x}-v\frac{\partial \zeta }{\partial y}\text{ },$ | (13) |
| ${{A}_{2}}=-\omega \frac{\partial \zeta }{\partial p}\text{ },$ | (14) |
| ${{A}_{3}}=-(f+\zeta )\delta \text{ },$ | (15) |
| ${{A}_{4}}=\frac{\partial \omega }{\partial y}\frac{\partial u}{\partial p}-\frac{\partial \omega }{\partial x}\frac{\partial v}{\partial p}\text{ },$ | (16) |
| ${{A}_{5}}=-\beta v\text{ },$ | (17) |
其中,p表示各等压面气压,β为罗斯贝参数,方程(11)左端A为涡度局地变化(倾向)项,右端A1为涡度平流项,A2为涡度垂直输送项,A3为涡度散度项,A4为涡度扭转项,A5为β效应项。
而由公式(10)对x求偏导,公式(9)对y求偏导,二者相加可得切变方程:
| $\begin{align} & \frac{\partial {{D}_{\rm{s}}}}{\partial t}=-\mathit{\boldsymbol{V}}\cdot \nabla {{D}_{\rm{s}}}-f{{D}_{\rm{t}}}-{{D}_{\rm{s}}}\delta - \\ & \ (\frac{\partial \omega }{\partial \mathit{y}}\frac{\partial \mathit{u}}{\partial \mathit{p}}\rm{+}\frac{\partial \omega }{\partial \mathit{x}}\frac{\partial \mathit{v}}{\partial \mathit{p}})\rm{+}\beta \mathit{v}\rm{-2}\mathit{g}\frac{{{\partial }^{\rm{2}}}\mathit{z}}{\partial \mathit{x}\partial \mathit{y}}. \\ \end{align}$ | (18) |
由公式(9)对x求偏导,公式(10)对y求偏导,二者相减可得到伸缩方程:
| $\begin{align} & \frac{\partial {{D}_{\rm{t}}}}{\partial t}=-\mathit{\boldsymbol{V}}\cdot \nabla {{D}_{\rm{t}}}+f{{D}_{\rm{s}}}-{{D}_{\rm{t}}}\delta -(\frac{\partial \omega }{\partial x}\frac{\partial u}{\partial p}-\frac{\partial \omega }{\partial y}\frac{\partial v}{\partial p})+ \\ & \quad \quad \quad \beta u-g\frac{{{\partial }^{2}}z}{\partial {{x}^{2}}}+g\frac{{{\partial }^{2}}z}{\partial {{y}^{2}}}. \\ \end{align}$ | (19) |
再由公式(18)乘以(Ds/D),公式(19)乘以(Dt/D),二者相加可得到总变形方程:
| $B={{B}_{1}}+{{B}_{2}}+{{B}_{3}}+{{B}_{4}}+{{B}_{5}}+{{B}_{6}}\text{ },$ | (20) |
其中,
| $B=\frac{\partial D}{\partial t}\text{ },$ | (21) |
| ${{B}_{1}}=-u\frac{\partial D}{\partial x}-v\frac{\partial D}{\partial y}\text{ },$ | (22) |
| ${{B}_{2}}=-\omega \frac{\partial D}{\partial p}\text{ },$ | (23) |
| ${{B}_{3}}=-D\delta \text{ },$ | (24) |
| ${{B}_{4}}=-\frac{{{D}_{\text{s}}}}{D}(\frac{\partial \omega }{\partial y}\frac{\partial u}{\partial p}+\frac{\partial \omega }{\partial x}\frac{\partial v}{\partial p})-\frac{{{D}_{\text{t}}}}{D}(\frac{\partial \omega }{\partial x}\frac{\partial u}{\partial p}-\frac{\partial \omega }{\partial y}\frac{\partial v}{\partial p})\text{ },$ | (25) |
| ${{B}_{5}}=\frac{{{D}_{\text{s}}}}{D}\beta v+\frac{{{D}_{\text{t}}}}{D}\beta u\text{ },$ | (26) |
| ${{B}_{6}}=-\frac{{{D}_{\text{s}}}}{D}(2g\frac{{{\partial }^{2}}z}{\partial x\partial y})-\frac{{{D}_{\text{t}}}}{D}(g\frac{{{\partial }^{2}}z}{\partial {{x}^{2}}}-g\frac{{{\partial }^{2}}z}{\partial {{y}^{2}}})\text{ },$ | (27) |
其中,方程(20)左端B为总变形局地变化(倾向)项,右端B1为总变形平流项,B2为总变形垂直输送项,B3为总变形散度项,B4为总变形扭转项,B5为β效应项,B6为水平气压(位势)梯度项。
在以往对高原低涡的分析中,人们往往用涡度来指示高原低涡的移动路径和强度(黄楚惠等,2010;田珊儒等,2015)。高原切变线与高原低涡都是高原及周边地区重要的灾害天气系统,两者往往伴随出现并且协同产生重要天气影响。在高原天气系统的研究和应用中,高原低涡和高原切变线总是习惯联系在一起,两者具有密切的联系,预报员也约定俗成地称这样的天气系统组合为“低涡切变”。为了更好研究高原低涡与切变线之间的关系,本文采用涡度方程和总变形方程来联合诊断高原低涡减弱、高原切变线生成机理及两者相互作用。
通过对比涡度、散度、切变以及伸缩的表达式[公式(2)、(7)、(4)和(3)]可以看出,涡度ζ和切变Ds中存在符号相反项
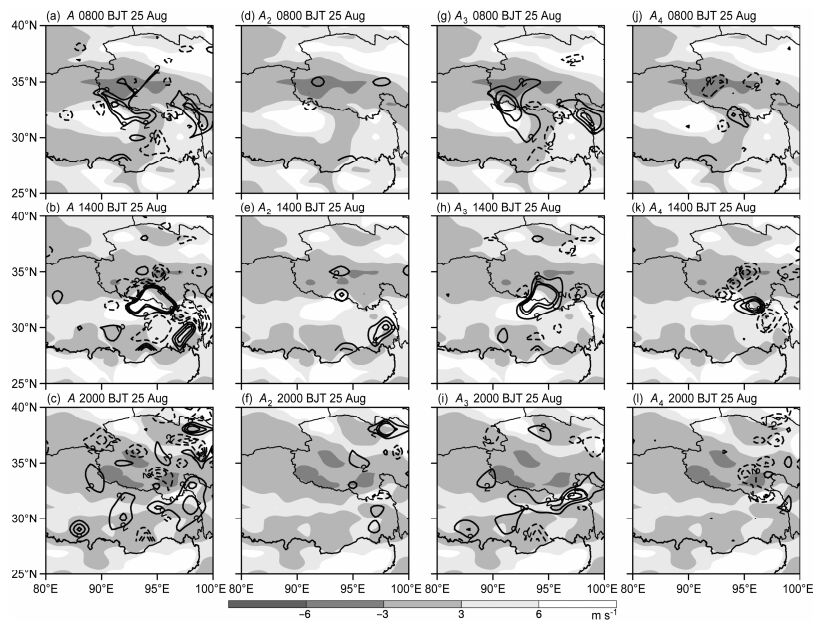
由图 8和图 9水平风场的纬向风u分量可以看出,u分量的分布与高原低涡和切变线的位置有很好的对应关系。2014年8月25日08时,在高原低涡南北两侧u分量存在两个正负大值中心,高原低涡就处于u分量梯度最大区内,此时的高原低涡强度较强;8月25日14时,高原低涡两侧的u分量中心强度减弱,并且呈椭圆状分布,高原低涡强度减弱,
|
图 8 2014年8月25日08时(上)、14时(中)、20时(下)500 hPa(a-c)涡度局地变化项(A,等值线,单位:10-9 s-2)、(d-f)涡度垂直输送项(A2,等值线,单位:×10-9 s-2)、(g-i)散度项(A3,等值线,单位:10-9 s-2)、涡度扭转项(A4,j-l,等值线,单位:10-9 s-2)和u分量(阴影,单位:m s-1)的时间演变。黑实(虚)线表示正(负)值,间隔:2×10-9 s-2 Figure 8 Temporal evolution of 500-hPa vorticity (a-c) local change term (A, contours, units: 10-9 s-2), (d-f) vertical transportation term (A2, contours, units: 10-9 s-2), (g-i) divergence term (A3, contours, units: 10-9 s-2), (j-l) twisting term (A4, contours, units: 10-9 s-2) in vorticity equation and u component (shaded, units: m s-1) of wind at 0800 BJT (top panels), 1400 BJT (middle panels), 2000 BJT (bottom panels) on 25 August 2014. Black solid (dashed) lines denote the positive (negative) values, intervals are 2×10-9 s-2 |

|
图 9 2014年8月25日08时(上)、14时(中)、20时(下)500 hPa(a-c)总变形局地变化项(B,等值线,单位:10-9 s-2)、(d-f)散度项(B3,等值线,单位:10-9 s-2)、(g-i)总变形扭转项(B4,等值线,单位:10-9 s-2)、(j-l)水平气压梯度项(B6,等值线,单位:10-9 s-2)和u分量(阴影,单位:m s-1)的时间演变。黑实(虚)线表示正(负)值,间隔:2×10-9 s-2 Figure 9 Temporal evolution of 500-hPa total deformation (a-c) local change term (B, contours, units: 10-9 s-2), (d-f) divergence term (B3, contours, units: 10-9 s-2), (g-i) twisting term (B4, contours, units: 10-9 s-2), (j-l) horizontal pressure gradient term (B6, contours, units: 10-9 s-2) in total deformation equation and u component (shaded, units: m s-1) of wind at 0800 BJT (top panels), 1400 BJT (middle panels), 2000 BJT (bottom panels) on 25 August 2014. Black solid (dashed) lines denote the positive (negative) values, intervals are 2×10-9 s-2 |
切变线上不仅有切变变形,还有伸缩变形,而总变形可以很好地反映切变线上切变和伸缩。高守亭(2007)对一次华北暴雨过程进行诊断分析时指出,对流层低层总变形场的大值带与切变线无论位置还是走向都几乎一致。本文在对总变形场进行分析时(图略),亦得出总变形场大值区的位置和强度与高原切变线有较好对应。
从动力学观点考虑,用涡度方程诊断与气旋性辐合相伴的高原低涡发展维持机制是合理的(冯伍虎和程麟生,2002;何光碧等,2009b)。通过计算涡度方程各项的数值可以得出β效应项比其他项小一个量级,又由于涡度平流项的主要作用是在系统内部搬运而不净产生涡度,故下面的讨论不包括涡度水平平流项和β效应项。从图 8可以看出,8月25日08时,高原低涡中心强度为1.56×10-4 s-1,在高原低涡中心以及前方为正涡度局地变化项的大值中心(中心值强度为7.4×10-9 s-2,位置为33°N,91°E),这有利于高原低涡加强东移;涡度垂直输送项为负值,也位于高原低涡中心,散度项(中心值强度为1.12×10-8 s-2,位置为33°N,91°E)和扭转项(中心值强度为4.6×10-9 s-2,位置为32°N,94°E)为正值。说明在垂直方向上涡度向高层输送,使得低层局地涡度减小,散度项和扭转项有助于低层局地涡度增加,并且散度项的影响比扭转项更强。8月25日14时,低涡中心的前方仍然为正的涡度局地变化项(中心值强度为1.77×10-8 s-2,位置为33°N,94°E),涡度局地变化中心值明显强于上一时刻。高原低涡中心的涡度减弱为1.36×10-4 s-1,并且呈东北—西南向的椭圆状分布。高原低涡这一形态变化主要受散度项(中心值强度为1.35×10-8 s-2,位置为33°N,95°E)的影响,散度项大值中心较上一时刻有所增强,散度项的增强与低涡区的散度(辐合)有关,由表 1可以看出低涡中心的涡度减弱,散度(辐合)较上一时刻明显增强,散度的增强是由于高原西北边的高压发展东伸,东边副高西伸北抬,两高压间的作用使辐合增强。这说明系统演变特征是由呈现强气旋性涡度的高原低涡演变为呈现强辐合的高原切变线。从散度项正值中心的形态分布可以看出,散度项实际上对高原低涡起到了拉伸的作用,使低涡的形状变为东北—西南向椭圆型,低涡强度减弱。在低涡前方,扭转项(中心值强度为1.13×10-8 s-2,位置为32°N,96°E)仍为正值,强度较上一时刻有所增强,使低涡继续东移到生成切变线的位置。8月25日20时,高原切变线生成,涡度场的中心强度减弱为8.9×10-5 s-1,正涡度带与高原切变线的位置较为一致。图 8c清楚表明,在切变线的前方,正涡度局地变化项呈东北—西南向的带状分布,预示高原切变线将东移。涡度垂直输送项为负值,散度项(中心值强度为8.1×10-9 s-2,位置为32°N,97°E)为正值,较上一时刻明显减弱,呈准纬向带状分布,很好地指示了高原切变线的东移。扭转项(中心值强度为3.9×10-9 s-2,位置为35°N,99°E)也明显减弱,位于高原切变线前方,有利于高原切变线东移。
| 表 1 500 hPa上高原低涡减弱、高原切变线生成过程中涡度、散度和总变形的演变 Table 1 The evolution of vorticity, divergence, and total deformation at 500 hPa during the process of plateau vortex weakening and plateau shear line forming |
同样的,总变形方程中β效应项为小项,可以不考虑总变形水平平流项和β效应的影响。从图 9(总变形垂直输送项影响范围较小,图中略去)可以看出,8月25日08时,在高原低涡的移动方向上,总变形的局地变化为负值,不利于总变形的加强。而在高原低涡的后方,总变形的局地变化项为正值,有利于总变形的发展。其中,在低涡的移动方向上散度项(中心值强度为3.0×10-9 s-2,位置为32°N,92°E)为正值且强度较弱,总变形扭转项(中心值强度为-4.9×10-9 s-2,位置为31°N,93°E)和气压梯度项(中心值强度为-1.25×10-8 s-2,位置为33°N,92°E)为负值,气压梯度项对总变形的影响较强。8月25日14时,在高原切变线生成位置上可以明显地看到,总变形局地变化项(中心值强度为1.01×10-8 s-2,位置为32°N,93°E)为正值,并且其水平分布与切变线形态较为一致。总变形散度项(中心值强度为4.9×10-9 s-2,位置为33°N,95°E)为正值,中心强度较上一时刻有所增强,并且其中心位置和形态分布与涡度方程中的散度项相一致,由表 1也可以看出在散度急剧增强的同时,总变形也在快速增长,说明总变形的增加可能是由于散度项的转换作用。总变形扭转项(中心值强度为1.01×10-8 s-2,位置为32°N,96°E)和水平气压梯度项(中心值强度为8.0×10-9 s-2,位置为33°N,93°E)也均为正值,有利于高原切变线的生成。8月25日20时,在高原切变线东移的前方,总变形局地变化项呈东北—西南向分布,但正负相间排列,说明总变形在切变线上的变化状态并不一致。总变形扭转项为负值,散度项和水平气压梯度项仍为正值。
综合以上分析可知,高原低涡从青海西南部向东移到高原切变线生成位置后减弱消失,高原切变线生成并东移发展。高原低涡东移主要受涡度方程中散度项和扭转项的影响,高原低涡的减弱主要是散度项作用。在高原低涡较强时,正涡度局地变化项呈纬向带状分布;当高原低涡减弱消失时,正涡度局地变化项呈现东北—西南向的带状分布,从这种形态上的变化可以看出高原低涡的减弱消失主要是受到拉伸变形造成的。而从总变形的变化态势可以看出,高原切变线的生成阶段,总变形局地变化项在切变线的生成位置上为正值,总变形扭转项对高原切变线的生成贡献最大,其次为水平气压梯度项,散度项的贡献最弱。
从以上高原低涡减弱、高原切变线生成机理分析不难理解,水平散度与伸缩变形之间存在相互转化,而这种转化关系也体现在涡度方程和总变形方程中。正是由于这种转化途径,散度项的作用使高原低涡被拉伸减弱、高原切变线生成。此个例高原切变线以伸缩变形为主,高原切变线沿变形场的拉伸轴分布。高原低涡受拉伸变形作用减弱消失,而正是由于这种拉伸变形作用有助于高原切变线的生成。说明在切变线上以拉伸变形为主时,不利于其上高原低涡的发展,切变线可能是影响低涡发展的背景流场。需要指出的是,高原切变线的生成在很大程度上受总变形扭转项和水平气压梯度项的影响,特别是当高原切变线移到高原的东侧边缘时,由于陡峭地形的作用,有利于出现较大水平风的垂直切变和垂直运动的水平切变,以及高原东坡陡增的水平气压梯度力,均对高原切变线的生成发挥有利的内在作用。
6 结论与讨论本文研究了一次从青海西南部东移的高原低涡减弱、高原切变线生成并在有利环流背景下得以东移发展引发川渝强降水的过程,得到以下三点结论:
(1) 可应用Okubo-Weiss(OW)参数来定量表达低涡、切变线气流中旋转性和变形性的相对大小,确定高原低涡的演化与高原切变线的潜在生成区域和发展态势。高原切变线生成阶段,500 hPa VOW值由正转负,VOW负值带可以很好地指示高原切变线的潜在生成区域。垂直方向上对流层整层气流以变形为主则有利于高原切变线的生成;高原切变线强降水阶段,500 hPa切变线区域以VOW负值控制为主。VOW负值大小与高原切变线强度有很好的相关性,用VOW负值可以指示高原切变线的发展状况。此个例高原切变线以伸缩变形为主。
(2) 通过涡度方程和总变形方程的联合诊断,初步揭示出高原低涡减弱、高原切变线生成的动力机制。高原低涡的减弱主要受散度项的影响,系统演变特征是由呈现强气旋性涡度的高原低涡演变为呈现强辐合的高原切变线。在高原低涡较强时,正涡度局地变化项呈纬向带状分布,当高原低涡减弱消失时,正涡度局地变化项呈现东北—西南向的带状分布。高原切变线的生成阶段,总变形局地变化项在切变线的生成位置上为正值,总变形扭转项对切变线生成的作用最强,其次为水平气压梯度项,散度项的贡献最弱。
(3) 高原低涡受拉伸变形作用减弱消失,而正是由于这种拉伸变形作用有助于高原切变线的生成。当高原切变线上以拉伸变形为主时,不利于其上高原低涡的发展,切变线可能是影响低涡发展的背景流场。
本文针对一次高原低涡和高原切变线的演变过程和机理分析,初步研究了高原低涡减弱、高原切变线生成的机理和演变特征。对于认识高原低涡和高原切变线的相互关系及其演变特征具有重要意义。但需要指出的是文中研究的个例只有一个,对于高原低涡和高原切变线的相互作用机理尚需多个例的分析支持。本文最后分析了高原切变线上有利于高原低涡发展的环境条件,但对于高原切变线背景下生成或诱发的高原低涡可能是由于切变变形转化为涡度而促使低涡生成的情形尚未开展研究。考虑到这一相互作用问题的复杂性,我们将通过另文对此进行专门探究。
| [] | Chen Lianshou, Luo Zhexian. 2003. A preliminary study of the dynamics of eastward shifting cyclonic vortices[J]. Adv. Atmos. Sci., 20(3): 323–332, DOI:10.1007/BF02690790. |
| [] | Dunkerton T J, Montgomery M T, Wang Z. 2009. Tropical cyclogenesis in a tropical wave critical layer:Easterly waves[J]. Atmos. Chem. Phys., 9(15): 5587–5646, DOI:10.5194/acp-9-5587-2009. |
| [] | 冯伍虎, 程麟生. 2002. "98.7"突发性特大暴雨中尺度切变线低涡发展的涡源诊断[J]. 高原气象, 21(5): 447–456. Feng Wuhu, Cheng Linsheng. 2002. Vorticity source diagnoses for the development of mesoscale low vortex with shearline during "98.7" abruptly extraordinary heavy rainstorm[J]. Plateau Meteor, 21(5): 447–456, DOI:10.3321/j.issn:1000-0534.2002.05.003. |
| [] | 高守亭. 2007. 大气中尺度运动的动力学基础及预报方法[M]. 北京: 气象出版社: 169-176. Gao Shouting. 2007. The Dynamical Basis and Predictive Method in Atmospheric Meso-scale Motion (in Chinese)[M]. Beijing: China Meteorological Press: 169-176. |
| [] | 高守亭, 周玉淑. 2001. 水平切变线上涡层不稳定理论[J]. 气象学报, 59(4): 393–404. Gao Shouting, Zhou Yushu. 2001. The instability of the vortex sheet along the horizontal shear line[J]. Acta Meteor. Sinica (in Chinese), 59(4): 393–404, DOI:10.11676/qxxb2001.043. |
| [] | 高守亭, 刘璐, 李娜. 2013. 近几年中尺度动力学研究进展[J]. 大气科学, 37(2): 319–330. Gao Shouting, Liu Lu, Li Na. 2013. Major advances in research on mesoscale atmospheric dynamics in recent years[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 37(2): 319–330, DOI:10.3878/j.issn.1006-9895.2012.12304. |
| [] | 何光碧. 2013. 高原切变线研究回顾[J]. 高原山地气象研究, 33(1): 90–96. He Guangbi. 2013. Review of the plateau shear-line studies[J]. Plateau Mountain Meteor. Res. (in Chinese), 33(1): 90–96, DOI:10.3969/j.issn.1674-2184.2013.01.016. |
| [] | 何光碧, 高文良, 屠妮妮. 2009a. 2000~2007年夏季青藏高原低涡切变线观测事实分析[J]. 高原气象, 28(3): 549–555. He Guangbi, Gao Wenliang, Tu Nini. 2009a. The observational analysis of shear line and low vortex over the Tibetan Plateau in summer from 2000 to 2007[J]. Plateau Meteor. (in Chinese), 28(3): 549–555. |
| [] | 何光碧, 高文良, 屠妮妮. 2009b. 两次高原低涡东移特征及发展机制动力诊断[J]. 气象学报, 67(4): 599–612. He Guangbi, Gao Wenliang, Tu Nini. 2009b. The dynamic diagnosis on easterwards moving characteristics and developing mechanism of two Tibetan Plateau vortex processes[J]. Acta Meteor. Sinica (in Chinese), 67(4): 599–612, DOI:10.11676/qxxb2009.060. |
| [] | 黄楚惠, 顾清源, 李国平, 等. 2010. 一次高原低涡东移引发四川盆地暴雨的机制分析[J]. 高原气象, 29(4): 832–839. Huang Chuhui, Gu Qingyuan, Li Guoping, et al. 2010. Mechanism analysis of plateau vortex moving east trigger rainstorm in Sichuan Basin[J]. Plateau Meteor. (in Chinese), 29(4): 832–839. |
| [] | 李江萍, 王式功, 孙国武. 2012. 高原低涡研究的回顾与展望[J]. 兰州大学学报(自然科学版), 48(4): 53–60, 71. Li Jiangping, Wang Shigong, Sun Guowu. 2012. Review and prospects of research on low vortex on the Qinghai-Tibetan Plateau[J]. J. Lanzhou Univ. (Nat. Sci.) (in Chinese), 48(4): 53–60, 71, DOI:10.3969/j.issn.0455-2059.2012.04.009. |
| [] | 李国平, 赵福虎, 黄楚惠, 等. 2014. 基于NCEP资料的近30年夏季青藏高原低涡的气候特征[J]. 大气科学, 38(4): 756–769. Li Guoping, Zhao Fuhu, Huang Chuhui, et al. 2014. Analysis of 30-year climatology of the Tibetan Plateau vortex in summer with NCEP reanalysis data[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 38(4): 756–769, DOI:10.3878/j.issn.1006-9895.2013.13235. |
| [] | 李国平, 卢会国, 黄楚惠, 等. 2016. 青藏高原夏季地面热源的气候特征及其对高原低涡生成的影响[J]. 大气科学, 40(1): 131–141. Li Guoping, Lu Huiguo, Huang Chuhui, et al. 2016. A climatology of the surface heat source on the Tibetan Plateau in summer and its impacts on the formation of the Tibetan Plateau vortex[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40(1): 131–141, DOI:10.3878/j.issn.1006-9895.1504.15125. |
| [] | 刘晓冉, 李国平. 2006. 青藏高原低涡研究的回顾与展望[J]. 干旱气象, 24(1): 60–66. Liu Xiaoran, Li Guoping. 2006. Review and prospect of research on the Tibetan Plateau vortex[J]. Arid Meteor. (in Chinese), 24(1): 60–66, DOI:10.3969/j.issn.1006-7639.2006.01.013. |
| [] | 刘云丰, 李国平. 2016. 夏季高原大气热源的气候特征以及与高原低涡生成的关系[J]. 大气科学, 40(4): 864–876. Liu Yunfeng, Li Guoping. 2016. Climatic characteristics of atmospheric heat source over the Tibetan Plateau and its possible relationship with the generation of the Tibetan Plateau vortex in the summer[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40(4): 864–876, DOI:10.3878/j.issn.1006-9895.1512.15184. |
| [] | 柳草, 李跃清, 李德俊. 2009. 高原低涡移出高原的动力结构特征分析[J]. 高原山地气象研究, 29(3): 8–11. Liu Cao, Li Yueqing, Li Dejun. 2009. Analysis on the dynamic structure of vortex moving out of the Tibetan Plateau[J]. Plateau Mountain Meteor. Res. (in Chinese), 29(3): 8–11, DOI:10.3969/j.issn.1674-2184.2009.03.002. |
| [] | 罗四维. 1992. 青藏高原及其邻近地区几类天气系统的研究[M]. 北京: 气象出版社: 14-25. Luo Siwei. 1992. Study on Some Kinds of Weather Systems over and around the Qinghai-Xizang Plateau (in Chinese)[M]. Beijing: China Meteorological Press: 14-25. |
| [] | 马林, 张青梅, 赵春宁, 等. 2003. 青藏高原东部牧区春季雪灾天气的形成及其预报[J]. 自然灾害学报, 12(3): 61–68. Ma Lin, Zhang Qingmei, Zhao Chunning, et al. 2003. Formation and forecast of spring snow-disaster weather in the eastern pasture-area of Qinghai-Xizang Plateau[J]. J. Nat. Disast. (in Chinese), 12(3): 61–68, DOI:10.3969/j.issn.1004-4574.2003.03.010. |
| [] | Petterssen S. 1956. Weather Analysis and Forecasting:Motion and Motion Systems V. 1[M]. New York: McGraw-Hill: 32-40. |
| [] | 青藏高原气象科学研究拉萨会战组. 1981. 夏半年青藏高原500毫巴低涡切变线的研究[M]. 北京: 科学出版社: 1-2. Lhasa Group of Tibetan Plateau Meteorology Research. 1981. Research of 500 mb Vortex and Shear Lines over the Tibetan Plateau in Summer (in Chinese)[M]. Beijing: Science Press: 1-2. |
| [] | 冉令坤, 李娜, 崔晓鹏. 2014. 登陆台风莫拉克(2009) 的涡度拟能收支分析[J]. 气象学报, 72(6): 1118–1134. Ran Lingkun, Li Na, Cui Xiaopeng. 2014. Analysis of the budget of enstrophy during the landing of Typhoon Morakot (2009)[J]. Acta Meteor. Sinica (in Chinese), 72(6): 1118–1134, DOI:10.11676/qxxb2014.088. |
| [] | Shen R, Reiter E R, Bresch J F. 1986. Numerical simulation of the development of vortices over the Qinghai-Xizang (Tibet) Plateau[J]. Meteor. Atmos. Phys., 35(1-2): 70–95, DOI:10.1007/BF01029526. |
| [] | 田珊儒, 段安民, 王子谦, 等. 2015. 地面加热与高原低涡和对流系统相互作用的一次个例研究[J]. 大气科学, 39(1): 125–136. Tian Shanru, Duan Anmin, Wang Ziqian, et al. 2015. Interaction of surface heating, the Tibetan Plateau vortex, and a convective system:A case study[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 39(1): 125–136, DOI:10.3878/j.issn.1006-9895.1404.13311. |
| [] | Tory K J, Dare R A, Davidson N E, et al. 2013. The importance of low-deformation vorticity in tropical cyclone formation[J]. Atmos. Chem. Phys., 13(4): 2115–2132, DOI:10.5194/acp-13-2115-2013. |
| [] | 屠妮妮, 何光碧. 2010. 两次高原切变线诱发低涡活动的个例分析[J]. 高原气象, 29(1): 90–98. Tu Nini, He Guangbi. 2010. Case analysis on two low vortexes induced by Tibetan Plateau shear line[J]. Plateau Meteor. (in Chinese), 29(1): 90–98. |
| [] | 王中, 陈艳英. 2007. 触发重庆山洪灾害的典型环流和影响系统分析[J]. 高原气象, 26(3): 609–614. Wang Zhong, Chen Yanying. 2007. Analyses on major effect systems and typical atmospheric circulation triggering mountain torrential disasters in Chongqing[J]. Plateau Meteor. (in Chinese), 26(3): 609–614, DOI:10.3321/j.issn:1000-0534.2007.03.024. |
| [] | 徐国昌. 1984. 500毫巴高原切变线的天气气候特征[J]. 高原气象, 3(1): 36–41. Xu Guochang. 1984. The climatologically synoptic characteri-stics of the shear line on the 500 mb surface over the Qinghai-Xizang Plateau[J]. Plateau Meteor. (in Chinese), 3(1): 36–41. |
| [] | 姚秀萍, 孙建元, 康岚, 等. 2014. 高原切变线研究的若干进展[J]. 高原气象, 33(1): 294–300. Yao Xiuping, Sun Jianyuan, Kang Lan, et al. 2014. Advances on research of shear convergence line over Qinghai-Xizang Plateau[J]. Plateau Meteor. (in Chinese), 33(1): 294–300, DOI:10.7522/j.issn.1000-0534.2013.00164. |
| [] | 叶笃正, 高由禧. 1979. 青藏高原气象学[M]. 北京: 科学出版社: 122-126. Ye Duzheng, Gao Youxi. 1979. Qinghai-Xizang Plateau Meteorology (in Chinese)[M]. Beijing: Science Press: 122-126. |
| [] | 叶笃正, 罗四维, 朱抱真. 1957. 西藏高原及其附近的流场结构和对流层大气的热量平衡[J]. 气象学报, 28(2): 108–121. Ye Duzheng, Luo Siwei, Zhu Baozhen. 1957. The wind structure and heat balance in the lower troposphere over Tibetan Plateau and its surrounding[J]. Acta Meteor. Sinica (in Chinese), 28(2): 108–121, DOI:10.11676/qxxb1957.010. |
 2017, Vol. 41
2017, Vol. 41


