2 成都信息工程大学大气科学学院/高原大气与环境四川省重点实验室, 成都 610225
2 School of Atmospheric Sciences/Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology, Chengdu 610225
气候预测和中期天气预报依赖于全球大气环流模式,而随着计算能力的提高,高分辨率全球数值天气预报已经进入视野,高效、高精度全球非静力数值模式开发在世界范围内相当流行。同时,高性能数值模式的开发首要是模式动力框架的发展,建立在球面准均匀网格上的全球大气数值模式研发正是当前数值预报的热点问题。现有的大气模式可以分为两类:一类是球面谱模式,借助于谱展开对连续方程进行离散化;另一类是格点模式,采用有限差分、有限体积或有限元等近似方法对连续方程离散化处理。
随着多核、乃至众核计算机的发展,格点模式发展正成为主流,通常的球面离散网格使用经纬度正交网格,可以方便球面矢量的描述和离散化计算。球面经纬度网格存在两个缺点:一是极点的坐标奇异性问题,无法描述极点处矢量,该缺陷可以通过对极地格点运用洛必达法则(Kageyama et al., 1995),或者将极地附近向量最小化诊断极点风速(Mcdonald and Bates, 2009)等方案来解决;二是经线在高纬区域辐合,使得网格距向高纬方向不断减小,从而限制模式时间步长的选取,该问题只能通过选择均匀网格来克服。综合可以看出,传统经纬度网格存在的问题都来自于高纬度网格,而在低纬度地区的计算性能较好,因此Kageyama and Sato(2004)提出了准均匀、无奇异点的“阴阳网格”,它是由两个完全相同的低纬度经纬网格组合而成的重叠网格系统。随着模式分辨率的不断提高,传统经纬度网格在高纬的计算问题越来越明显,因此阴阳网格对全球高分辨率模式的发展具有重要意义。目前阴阳网格已经被应用于浅水波方程(李兴良, 2007; Qaddouri et al., 2008; Qaddouri, 2011)和三维大气模式(Baba et al., 2010; Qaddouri and Lee, 2011; Li et al., 2015)的开发。
作为一种重叠网格,阴阳网格也存在一些缺点。首先,阴阳网格存在重合部分和内部边界,需要插值和数据通信来实现全球数值计算,而重合区也存在离散点的代表性问题。其次,由于内部边界的存在,阴阳网格不能自然保证物理量(如质量、动量、能量)的全球守恒性,需要额外的数值手段实现。物理量的守恒特性对于模式的长期稳定积分十分重要,因此构建阴阳网格的全球和局地质量守恒算法对于高分辨率大气数值模式的发展非常必要。Peng et al.(2006)在单元格内质量均匀分布的假定下,通过强迫阴阳网格边界的通量一致性来实现阴阳网格的质量全球守恒计算,并在通量形式平流方程上利用CIP-CSLR平流方案(Constrained Interpolation Profiles-Conservative Semi-Lagrangian with Rational function; Xiao et al., 2002)检验和验证了该守恒算法。李江浩和彭新东(2013)在此基础上假设网格内质量双线性分布,初步构建了具有次网格结构的高精度质量守恒改进方法。Zerroukat and Allen(2015)利用低阶方案的单调性和高阶方案的精确性,综合利用高、低阶两个方案在平流方程上实现了全球质量的单调和守恒计算,但该方案的缺点是无法保证局地守恒,并且需要利用两个分辨率分别计算,增加了计算负担。
为了进一步改进阴阳网格全球和局地守恒强迫算法(Peng et al., 2006),本文除考虑网格内质量双线性分布外,同时考虑阴阳网格边界的通量为线性分布,以改进边界通量的分布和守恒强迫计算精度。为了方便,本文称该方案为MFL,而原始方案(Peng et al., 2006)基于网格内质量和通量均匀分布,标记为MFC方案。以下主要介绍MFL守恒强迫方法的构建和采用CIP-CSLR平流方案(Xiao et al., 2002)求解通量形式平流方程对两种方案进行对比评估,讨论MFL改进方案的计算效果和数值误差增长。
2 阴阳网格简介阴阳网格(Kageyama and Sato, 2004, 图 1)是由两个普通经纬度网格的低纬区域经过对称旋转合并而成,类似于网球或棒球的构造,其中旋转的区域我们称为阴网格(图 1a),没有旋转的区域称为阳网格(图 1b),阳网格和阴网格具有完全相同的局地经纬度范围和网格构造,阳网格的经、纬度坐标范围为

|
图 1 阴阳网格构造示意图:(a)阴网格;(b)阳网格;(c)阴阳网格 Figure 1 Schematic diagram of the Yin–Yang grid: (a) Yin grid; (b) Yang grid; (c) Yin–Yang grid |
| $ \left\{ {\begin{array}{*{20}{c}} {\pi/4 - \varepsilon \le \lambda \le 7\pi/4 + \varepsilon ,}\\ { - \pi/4 - \varepsilon \le \phi \le \pi/4 + \varepsilon ,} \end{array}} \right. $ | (1) |
其中,λ是经度,ϕ是纬度,ε是为了保证网格相互重叠而向外扩展的网格区域,因此阴阳网格构成了一个可以描述整个球面的重叠网格系统。在笛卡尔坐标系中,阴阳网格之间的转换关系为
| $ \left( {{x^{\rm n}},{y^{\rm n}},{z^{\rm n}}} \right) = \left( { - {x^{\rm e}},{z^{\rm e}},{y^{\rm e}}} \right), $ | (2) |
其中,n代表阳网格,e代表阴网格。
阴阳网格具有以下优点:
(1)阴阳网格不包含数学极点,因此不存在奇异性问题。
(2)阴阳网格是由普通经纬度网格的低纬度区域组成的,所以网格具有准均匀性,因此各网格在计算线性稳定性条件下所容许的时间步长基本一致,可提高计算效率。
(3)阴阳网格是相互旋转对称,对称性不因网格位置的改变而改变,阴阳网格区域的选择具有很大的灵活性。
(4)由于阴阳网格的基本构成元素为普通经纬度网格,基于经纬度网格发展的数值算法都可以方便地应用于阴阳网格中。
3 平流方案和网格配置 3.1 CIP-CSLR平流方案简介考虑平流计算的守恒性,我们选用基于有限体积法构建的CIP-CSLR方案对通量型平流方程进行求解。有限体积法与半拉格朗日法结合,不仅发挥了半拉格朗日方法的高计算效率,而且可以保证计算守恒,还可采用高阶空间插值,从而获得较高的计算精度,已经被广泛应用于天气和气候的数值模式预报(陈嘉滨和季仲贞, 2004)。CIP-CSLR平流方案(Xiao et al., 2002)就是在有限体积概念下,利用有理函数的正定性,给出的半拉格朗日物质平流计算方案,它具有正定、保形、绝对稳定的特点。一维无辐散的通量形式平流方程:
| $\frac{{\partial {\rho _i}}}{{\partial t}} + \frac{{{{\left( {uf} \right)}_{i + 1/2}} - {{\left( {uf} \right)}_{i - 1/2}}}}{{\Delta {x_i}}} = 0,$ | (3) |
其中,ρi代表单元格积分平均值,f代表单元格界面值,(uf)i+1/2即为通过网格边界的通量,△xi为网格距。
该方法利用单元格积分平均值和单元格界面值构造有理函数,同时结合半拉格朗日后向追踪法,重构上游点的单元格界面值,进而得到界面处的质量通量,然后通过通量形式平流方程计算下一时刻的单元格积分平均值,从而实现通量形式平流方程的守恒计算。
对于二维、三维平流方程,CIP-CSLR平流方案通过分维算法多次求解一维平流方程来实现,一方面运算比较简便,另一方面也能保证准确性和稳定性(Xiao et al., 2002)。
3.2 平流方程和网格配置对于二维平流问题,我们考虑无辐散条件下的通量方程:
| $\frac{{\partial q}}{{\partial t}} + \frac{\partial }{{\partial \lambda }}\left( {\bar uq} \right) + \frac{\partial }{{\partial \left( {\sin \phi } \right)}}\left( {\bar vq} \right) = 0,$ | (4) |
其中,q代表被平流的物理量,u=u/(acosϕ),v=vcosϕ/a,a表示地球半径,u,v分别表示风的纬向和经向分量,由于阴阳网格的守恒强迫只涉及水平方向的计算问题,本文只考虑水平方向的平流。
采用的网格为多变量矩的M网格,也就是所有矢量和标量在网格中心和边界中央都有离散值,相当于Arakawa-A网格和Arakawa-C网格的结合。阴阳网格边界物理量主要采用插值方法来进行数据交换,这里我们采用双线性插值法(Peng et al., 2006)计算,该方法具有计算简便的特点,同时能保证边界插值计算的单调性。
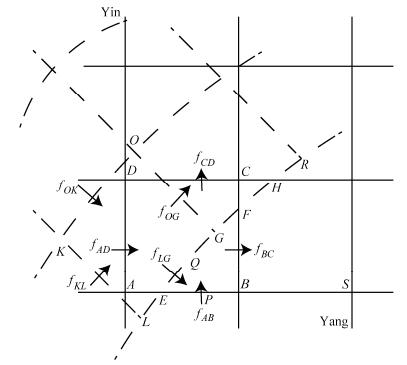
4 阴阳网格质量和边界通量线性分布计算图 2给出了阴阳网格质量、边界通量重构计算示意图,其中f代表通量。Peng et al.(2006)详细描述了阴阳网格守恒强迫(MFC方案)算法的具体计算过程,MFC方案是指在计算边界通量时假定单元格内质量分布均匀,即单元格积分平均值代表网格平均质量,从而强迫阴阳网格边界通量收支平衡,修正边界网格上的通量(假设通量在边界上均匀分布),达到质量守恒的目的。MFL方案是指利用单元格积分平均值和界面值构造质量的双线性分布,同样通过强迫边界通量收支平衡,修正边界网格通量(假设通量在边界上线性分布),实现质量守恒。这里我们说明网格质量双线性分布和边界通量线性分布的MFL方案构建和主要计算步骤(图 2):
|
图 2 阴阳网格质量、通量重构计算示意图。虚线:阴网格;实线:阳网格 Figure 2 The schema of quality and flux reconstruction on Yin (dashed lines) and Yang (solid lines) grids |
(1)根据阴阳网格坐标的相对位置和转换关系确定阴阳网格交点位置,如E和F,进而得到AE、EF、CF的长度。
(2)利用阴阳网格经纬线方程,计算网格重合部分的面积,如SAEFCD。
(3)通过阴阳网格坐标转换关系,计算阴网格边界上的点G落在阳网格内的位置,得到EG、GF的长度。
(4)利用CIP-CSLR平流方案,在阴阳网格各自的坐标系中计算通量,如fAB、fBC、fAD、fCD。MFC中通量均匀分布方案为fAE=(AE/AB)fAB,而MFL方案中假设通量沿边界线性分布,某一线段上的累加通量分布函数为f=k1x2+m1x,其中,x是从A点开始到单元格内某一位置P点的距离,f是通过AP的通量。利用AB和BS两个单元格的格距和通量,可以求出k1和m1,从而确定通量fAE。
(5)单元格AEFCD的质量通过单元格积分平均值和界面值构造双线性分布。强迫阴或阳网格内单元格AEFCD两个时次之间的质量变化=单元格AEFCD的通量变化,求出通量fEF。
(6)求出阴网格边界通量fEG、fGF。假设边界累加通量分布函数f=k2x2+m2x,其中,x是从E点开始到单元格内某一位置Q的距离,f是通过EQ的通量。利用阴网格被阳网格切割部分EF和FH的网格距离和通量,可以求出k2和m2,进而利用通量函数求出fEG和fGF。
(7)对阴阳网格边界处所有的被切割网格重复步骤(4)至(6),可以算出所有阴网格边界上新的通量,如fLG。
(8)通过通量形式平流方程求出单元格LGOK下一时刻的积分值q。
5 理想试验及结果本文采用广泛应用的“余弦钟”平流试验(Williamson et al., 1992)、正弦波试验(Li et al., 2012)和变形流试验(Nair et al., 1999)对MFL和MFC方案进行对比平流计算和分析。
在阴阳网格中,任意一个标量q在整个球面上的积分量M(q)(Peng et al., 2006)为
| $ \begin{array}{l} M\left( q \right) = \frac{1}{{4\pi}}\int_{\frac{\pi}{4}}^{\frac{{7\pi}}{4}} {\int_{{\rm{ - }}\frac{\pi}{4}}^{\frac{\pi}{4}} {{q_{\rm {Yin}}}\left( {\lambda ,\phi } \right)\cos \phi \rm {d} \phi \rm {d} \lambda } } {\rm{ + }}\\ \frac{1}{{4\pi}}\int_{\frac{\pi}{4}}^{\frac{{7\pi}}{4}} {\int_{{\rm{ - }}\frac{\pi}{4}}^{\frac{\pi}{4}} {{q_{\rm {Yang}}}\left( {\lambda ,\phi } \right)\cos \phi \rm {d}\phi \rm {d}\lambda } } - {M_0}, \end{array} $ | (5) |
| $ \begin{array}{l} {M_0} = \frac{1}{{4\pi}}\int {\int_{\rm {overset}} {{q_{\rm {Yin}}}\left( {\lambda ,\phi } \right)\cos \phi } } \rm {d} \phi \rm {d} \lambda = \\ \frac{1}{{4\pi}}\int {\int_{\rm {overset}} {{q_{\rm {Yang}}}\left( {\lambda ,\phi } \right)\cos \phi } } \rm {d} \phi \rm {d} \lambda , \end{array} $ | (6) |
其中,qYin(λ, ϕ)代表阴网格上的标量,qYang(λ, ϕ)代表阳网格上的标量,M0代表阴阳网格重叠部分的积分量。
标准化误差定义(Williamson et al., 1992)为
| ${L_1} = \frac{{M\left[ {q\left( {\lambda ,\phi } \right) - {q_{\rm T}}\left( {\lambda ,\phi } \right)} \right]}}{{M\left[ {{q_{\rm T}}\left( {\lambda ,\phi } \right)} \right]}},$ | (7) |
| ${L_2} = \frac{{{{\left\{ {M\left[ {{{\left( {q\left( {\lambda ,\phi } \right) - {q_{\rm T}}\left( {\lambda ,\phi } \right)} \right)}^2}} \right]} \right\}}^{\frac{1}{2}}}}}{{{{\left\{ {M\left[ {{q_{\rm T}}{{\left( {\lambda ,\phi } \right)}^2}} \right]} \right\}}^{\frac{1}{2}}}}},$ | (8) |
| $ \begin{array}{l} {L_{\inf}} = \\ \frac{{\max\left[ {\left| {{q_{\rm {Yin}}}\left( {\lambda ,\phi } \right) - {q_{\rm {Yin,T}}}\left( {\lambda ,\phi } \right)} \right|,{\rm{ }}\left| {{q_{\rm {Yang}}}\left( {\lambda ,\phi } \right) - {q_{\rm {Yang,T}}}\left( {\lambda ,\phi } \right)} \right|} \right]}}{{\max\left[ {\left| {{q_{\rm {Yin,T}}}\left( {\lambda ,\phi } \right)} \right|,{\rm{ }}\left| {{q_{\rm {Yang,T}}}\left( {\lambda ,\phi } \right)} \right|} \right]}}, \end{array} $ | (9) |
其中,q(λ, ϕ)代表平流量的数值解,qT(λ, ϕ)代表平流量的解析解。由公式可看出,标准化误差代表数值解与解析解的相对误差,L1、L2表示误差的平均分布,Linf表示局地误差的极值,标准化误差越小,代表数值解越精确。
5.1 “余弦钟”平流试验“余弦钟”平流试验(Williamson et al., 1992)是一个刚体平流试验,它描述的是一个孤立的余弦波在球面上被无辐散风场平流的过程。标量场的初始分布为
| $ q\left( {\lambda ,\phi } \right) = \left\{ {\begin{array}{*{20}{c}} {0, r \ge R,} \\ {\frac{1}{2}\left( {\cos\frac{{\pi r}}{R} + 1} \right), r < R,} \end{array}} \right. $ | (10) |
其中,R=a/3,r=a arccos[cosϕ0cosϕcos(λ-λ0)+sinϕ0sinϕ]表示球面任意位置(λ,ϕ)与“余弦钟”中心(λ0,ϕ0)的距离,(λ0,ϕ0)的初始值为(π/2, 0)。平流运动的无辐散风场为
| $u = {u_0}\left( {\sin\phi \cos\lambda \sin\alpha + \cos\phi \cos\alpha } \right),$ | (11) |
| $v = - {u_0}\sin\lambda \sin\alpha ,$ | (12) |
其中,α是“余弦钟”的旋转轴和球坐标系极轴的夹角,u0=2πa/(12d),即“余弦钟”的平流周期是12 d。
本试验选取分辨率为2.25°×2.25°,CFL=0.5(CFL
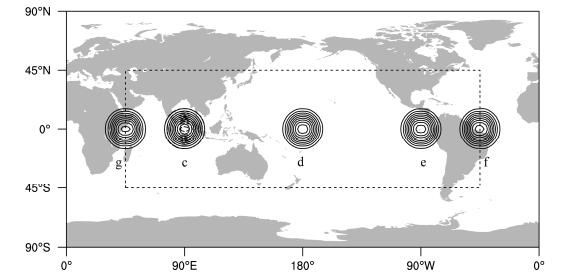
当α=0°时,MFL方案计算“余弦钟”随时间的状态变化如图 3所示,由图可知,“余弦钟”在平流过程中基本未发生形变,尤其是在通过阴阳网格边界(g, f)时,也能较好的保持原来的形状,且在运动一个周期(12 d)后,能够回到原来的初始位置,仅在最大值附近出现数值扩散,该试验验证了MFL方案在球面平流计算过程中的有效性。
|
图 3 α=0°时,MFL方案“余弦钟”平流12 d标量场的分布(等值线从0.1到0.9,间隔是0.1),平流顺序为c(实线)→d→e→f→g→c(虚线),点线为阴阳网格的分界线(下同) Figure 3 The distribution of a scalar quantity of "cosine bell" during 12-day advection with MFL scheme (a mass-conservative algorithm of cell-wise bi-linear mass distribution and piece-wise linear flux distribution over the boundary) at α=0°. The contours are plotted from 0.1 to 0.9 with an interval of 0.1, the bell rotates in an order from c (solid lines)→d→e→f→g→c (dashed lines). The dotted line shows the boundary of the Yin and Yang grids, the same hereafter |
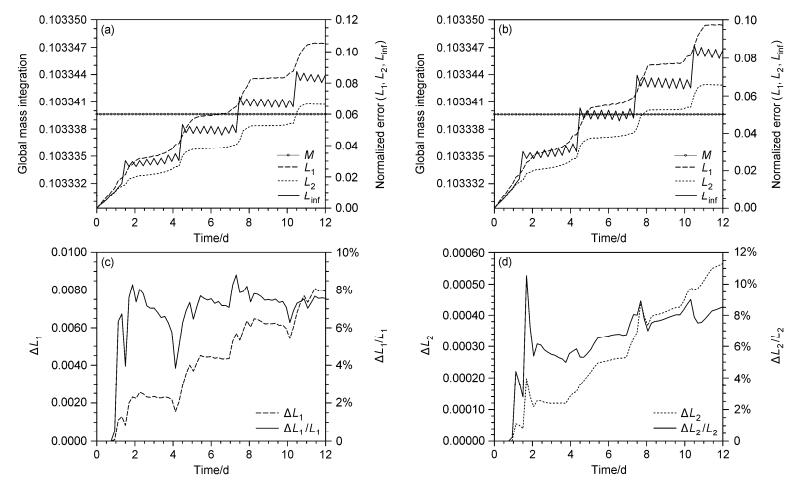
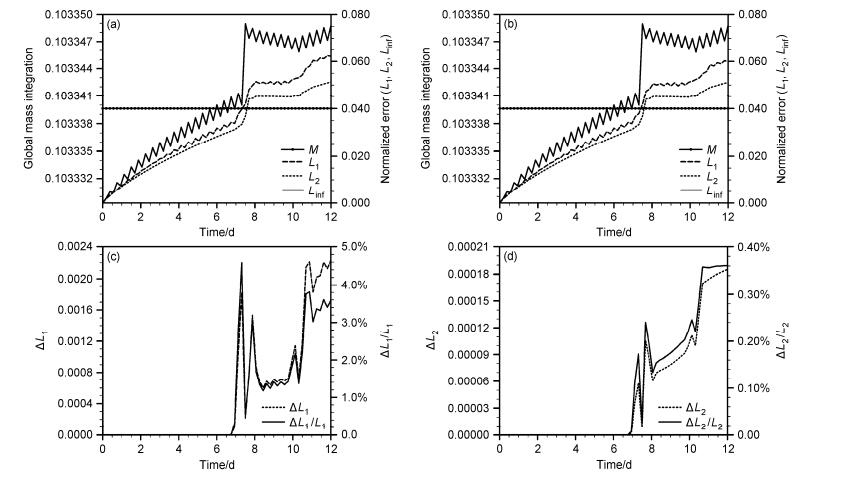
为了进一步验证MFL方案的精度,我们计算了两种方案下“余弦钟”平流12 d的积分总质量和标准化误差随时间的演变。如图 4a、b所示,在两种方案下,全球积分总质量都能保持守恒,并且结合图 3可看出,在经过阴阳网格边界时,误差会显著增加,说明了提高阴阳网格边界插值和守恒强迫方案精度的必要性。由图 4c、d的误差对比可见,在12 d的积分过程中MFL方案比MFC方案的精度有所提高,由于前6 d“余弦钟”在阳网格内部运动,还没有穿越阴阳网格边界,且“余弦钟”位于阳网格中央,不受边界处理影响,两种方案的误差基本相同。在第6~12 d,MFL方案比MFC方案的误差L1最多减小了4.8%,误差L2最多减小了0.38%。由于被平流的“余弦钟”占球面面积较小,远离阴阳网格边界,且只通过边界2次,本试验中两种方案的误差差异不大。
|
图 4 α=0°时,(a)MFC方案和(b)MFL方案计算“余弦钟”平流的全球积分总质量(左轴)和标准化误差(L1、L2、Linf,右轴)随时间变化,(c)MFC方案与MFL方案的L1之差△L1(左轴)和△L1/L1(右轴)随时间变化,(d)MFC方案与MFL方案的L2之差△L2(左轴)和△L2/L2(右轴)随时间变化 Figure 4 Temporal evolutions of global mass integration (left axis) and the normalized errors (L1, L2, Linf, right axis) of "cosine bell" advection with schemes (a) MFC (a mass-conservative algorithm of cell-wise constant mass distribution and piece-wise constant flux distribution over the boundary) and (b) MFL at α=0°, (c) temporal evolutions of △L1 (the difference between L1 of MFC scheme and L1 of MFL scheme, left axis) and △L1/L1 (right axis), (d)△L2 (the difference between L2 of MFC scheme and L2 of MFL scheme, left axis) and △L2/L2 (right axis) at α=0° |
当风向改为α=90°,MFL方案下“余弦钟”在通过南北极后仍然保持原来的形状,可见在阴阳网格中不存在极区经线辐合和极点奇异问题,降低了极区附近的平流变形。事实上,对于阴阳网格而言,沿赤道的纬向平流和过极点的经向平流非常相似,两种情况仅有初始位置不同而导致穿越阴阳网格边界的次数有差异。相比α=0°时,α=90°时被平流物通过阴阳网格边界的次数(4次)增多,但基本未发生形变,在平流一个周期后,保持形状回到初始位置。
图 5给出了α=90°时两种方案的全球积分总质量和标准化误差对比。可见,MFL方案和MFC方案的全球积分总质量可以保持守恒,“余弦钟”通过阴阳网格边界时,误差也会显著增加(4次)。由图 5c、d可知,在平流12 d的过程中,MFL方案比MFC方案的标准化误差L1最多减少了9%,L2最多减少了1.1%,误差比α=0°时减小的幅度大,主要原因是通过边界的次数增多,反映了MFL方案对处理边界通量和全球平流计算精度的改进。
5.2 正弦波试验正弦波试验(Li et al., 2012)是一种较为平缓的理想试验,它的初始场(高度场)分布为
| $q\left( {\lambda ,{\rm{ }}\phi } \right) = {\cos ^2}\phi \sin \left( {2\lambda } \right),$ | (13) |
无辐散风场与“余弦钟”平流相同:
| $u = {u_0}\left( {\sin\phi \cos\lambda \sin\alpha + \cos\phi \cos\alpha } \right),$ | (14) |
| $v = - {u_0}\sin\lambda \sin\alpha ,$ | (15) |
其中,(λ, ϕ)表示球面上任意一点的经度和纬度,α是球坐标极轴和旋转方向的夹角,u0=2πa/(12d),正弦波试验的周期为12 d。
本试验选取网格分辨率为2.25°×2.25°,CFL=0.5,积分步长为3240 s,在上述条件下,分别选取α=45°和α=90°两个旋转方向来对比MFL和MFC方案。
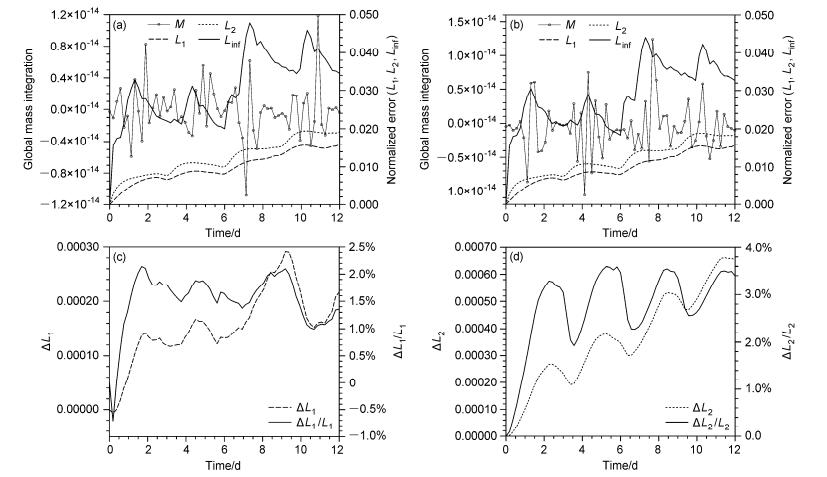
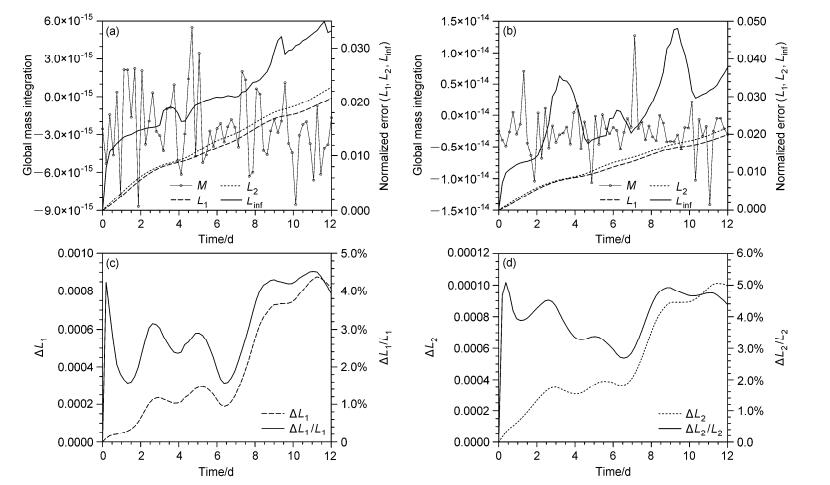
当α=45°时,MFL和MFC方案的全球总质量,标准化误差的对比如图 6所示,由图 6a、b可知,在计算机的误差范围内,两种方案都能保持全球质量守恒,由于正弦波试验的高度场分布面积广,且空间变化梯度小,误差的变化也比较平缓,误差增长相对较小。由图 6c、d可知,在一个周期内,新方案相对于原方案L1减小的百分比最多为4.5%,L2减小的百分比最多为5%,MFL方案比MFC方案的精度有所提高,误差L1相对“余弦钟”平流试验改进较少,主要原因是由于边界处标量的变化梯度比较小。
|
图 6 α=45°时,(a)MFC方案和(b)MFL方案计算正弦波试验的全球积分总质量(左轴)和标准化误差(L1、L2、Linf,右轴)随时间变化,(c)MFC方案与MFL方案的L1之差△L1(左轴)和△L1/L1(右轴)随时间变化,(d)MFC方案与MFL方案的L2之差△L2(左轴)和△L2/L2(右轴)随时间变化 Figure 6 Temporal evolutions of global mass integration (left axis) and normalized errors (L1, L2, Linf, right axis) in sine wave test with schemes (a) MFC and (b) MFL at α=45°, (c) temporal evolutions of △L1 (left axis) and △L1/L1 (right axis), (d)△L2 (left axis) and △L2/L2 (right axis) at α=45° |
对于α=90°的情形,两种方案的全球总质量和标准化误差随时间的变化如图 7所示,由图 7a、b可知,两种方案都能保证全球总质量守恒,高度场分布在阴阳网格边界处有明显的起伏变化,所以标准化误差在随时间变化过程中也会有明显的起伏增长过程,积分12 d内,L1最多减小了2.2%,L2最多减小了3.6%。
5.3 变形流试验变形流试验(Nair et al., 1999; Li et al., 2013)是在旋转坐标系上同时生成的两个对称的涡旋。在旋转坐标系(λ', ϕ')下,切线方向速度Vta、径向速度Vr、角速度w'(ϕ)'分布为
| $ {V_{\rm {ta}}}={{3\sqrt 3 \tanh \left( {r'} \right){{{{\rm sech}} }^2}\left( {r'} \right)} / 2}, $ | (16) |
| ${V_{\rm r}} = {{{\rm{d}}\phi '} / {{\rm{d}}t}} = 0,$ | (17) |
| $ w'\left( {\phi '} \right) = \left\{ {\begin{array}{*{20}{c}} {{{{V_{\rm {ta}}}} / {r'}},r' \ne 0,}\\ {0, r' = 0,} \end{array}} \right. $ | (18) |
其中,r'=r0cosϕ',r0=3。
标量解析解表达式为
| $q\left( {\lambda ',\phi ',t} \right) = 1 - \tanh \left\{ {\frac{{r'}}{d}\sin (\lambda ' - \omega 't)} \right\},$ | (19) |
其中,d=5。
旋转坐标系(λ', ϕ')与球面坐标系(λ,λ)的转换关系为
| $\lambda '\left( {\lambda ,\phi } \right) = \arctan \left[ {\frac{{\sin \left( {\lambda - {\lambda _0}} \right)}}{{\sin {\phi _0}\cos \left( {\lambda - {\lambda _0}} \right) - \cos {\phi _0}\tan \phi }}} \right],$ | (20) |
| $\phi '\left( {\lambda ,\phi } \right) = \arcsin \left[ {\sin \phi \sin {\phi _0} + \cos \phi \cos {\phi _0}\cos \left( {\lambda - {\lambda _0}} \right)} \right].$ | (21) |
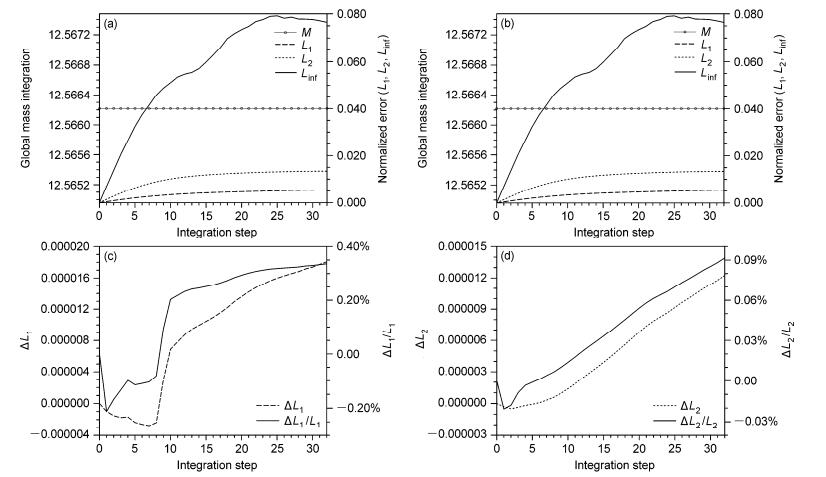
本试验中我们将涡旋中心放在(π/4, 0)和(3π/4, 0),网格分辨率为2.25°×2.25°,CFL=0.5,积分步长为166单位,变形流流场随积分步数的变化如图 8所示。数值解与解析解的差值主要分布在变形流的涡旋中心,阴阳网格交界处并无特别大误差。图 9是MFL方案和MFC方案全球积分总质量和标准化误差的对比图,变形流试验中,在保持质量守恒的情况下,两种方案的标准化误差增加都比较缓慢,误差集中在涡旋中心的变形密集区,由图 9c、d可以看出,MFL方案的误差比MFC方案的误差有所减小,在积分32步后,L1减小了0.35%,L2减小了0.09%,两种方案的误差差异较小,这主要与误差集中在涡旋中心有关,同时边界处标量变化的梯度比较小,所以边界处理对计算结果影响不大。

|
图 8 MFL方案变形流试验(a)初始场、(b)积分10步、(c)积分20步和(d)积分32步的高度场(阴影)分布,等值线(等值线从−0.05到0.05,间隔是0.02)代表数值解与解析解的差值 Figure 8 Height field in the deformational flow test with MFL scheme: (a) Initial condition, and integration after (b) 10, (c) 20, and (d) 32 steps (shaded areas). The contours (contours from −0.05 to 0.05 with an interval of 0.02) show differences between the numerical and analytical solutions |
|
图 9 (a)MFC方案和(b)MFL方案在变形流试验中的全球积分总质量(左轴)和标准化误差(L1、L2、Linf,右轴)随时间变化;(c)MFC方案与MFL方案的误差之差△L1(左轴)和△L1/L1(右轴)随时间变化,(d)MFC方案与MFL方案的误差之差△L2(左轴)和△L2/L2(右轴)随时间变化 Figure 9 Temporal evolutions of global mass integration (left axis) and normalized errors (L1, L2, Linf, right axis) in deformational flow test with schemes (a) MFC and (b) MFL, (c) temporal evolutions of △L1 (left axis) and △L1/L1 (right axis), and (d)△L2 (left axis) and △L2/L2 (right axis) |
在假定阴阳网格边界通量线性分布和网格内质量双线性分布的前提下,构建了阴阳网格MFL全球守恒强迫方案,该方案利用计算网格内的多种信息可分辨次网格质量分布和边界通量的网格尺度变化。采用CIP-CSLR平流方案对通量形式平流方程求解,利用“余弦钟”平流试验、正弦波试验、变形流试验进一步检验了MFL方案的精度和计算效果,分别对MFL方案和MFC方案进行了对比,总体而言,MFL方案改善了阴阳网格的球面平流计算结果,并满足了全球守恒计算要求。在三个理想试验中,MFL方案都表现出优于MFC方案的性能,误差相对MFC方案有所减小。“余弦钟”平流试验标量场的变化梯度在阴阳网格交界处最大,表现出的误差减小幅度也最大,能达到5%~10%,另外两个试验表现出的误差减小百分比略小。另一方面,在考虑质量双线性分布和边界通量的线性分布时,MFL新强迫方案在改善全球质量守恒计算的同时,并没有明显的计算负担,具有实际应用价值。
本文仅对阴阳网格的守恒算法在平流方程上的应用进行了讨论,阴阳网格作为一种新型网格,它在二维浅水波模式以及三维模式中的应用也得到发展,目前已经在GRAPES模式中得到应用。对于气候变化研究而言,阴阳网格的守恒算法将对模式长期积分具有重要意义,也是充分发挥阴阳网格优势的基础上减少模式气候态飘移的有效手段,因此也是阴阳网格广泛应用的关键。
| [] | Baba Y, Takahashi K, Sugimura T, et al. 2010. Dynamical core of an atmospheric general circulation model on a Yin-Yang grid[J]. Mon. Wea. Rev., 138(10): 3988–4005, DOI:10.1175/2010MWR3375.1. |
| [] | 陈嘉滨, 季仲贞. 2004. 半隐式半拉格朗日平方守恒计算格式的构造[J]. 大气科学, 28(4): 527–535. Chen Jiabin, Ji Zhongzhen. 2004. A study of complete square-conserving semi-implicit semi-Lagrangian scheme[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 28(4): 527–535, DOI:10.3878/j.issn.1006-9895.2004.04.05. |
| [] | Kageyama A, Sato T. 2004. "Yin-Yang grid":An overset grid in spherical geometry[J]. Geochem. Geophys. Geosyst., 5(9): Q09005, DOI:10.1029/2004GC000734. |
| [] | Kageyama A, Sato T, the Complexity Simulation Groups. 1995. Computer simulation of a magnetohydrodynamic dynamo. Ⅱ[J]. Phys. Plasmas, 2(5): 1421–1431, DOI:10.1063/1.871485. |
| [] | 李江浩, 彭新东. 2013. 阴阳网格上质量守恒计算性能分析[J]. 大气科学, 37(4): 852–862. Li Jianghao, Peng Xindong. 2013. Analysis of computational performance of conservative constraint on the Yin-Yang grid[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 37(4): 852–862, DOI:10.3878/j.issn.1006-9895.2012.12060. |
| [] | 李兴良. 2007. 球面阴阳网格与新型多离散矩有限体积方法的应用研究[D]. 南京信息工程大学博士学位论文. Li Xingliang. 2007. On the spherical Yin-Yang grid and application of a novel multi-moment finite volume method[D]. Ph. D. dissertation (in Chinese), Nanjing University of Information Science & Technology. http: //cdmd. cnki. com. cn/article/cdmd-10300-2007127482. htm |
| [] | Li X H, Peng X D, Li X L. 2015. An improved dynamic core for a non-hydrostatic model system on the Yin-Yang grid[J]. Adv. Atmos. Sci., 32(5): 648–658, DOI:10.1007/s00376-014-4120-5. |
| [] | Li X L, Shen X S, Peng X D, et al. 2012. Fourth order transport model on Yin-Yang grid by multi-moment constrained finite volume scheme[J]. Proc. Comput. Sci., 9: 1004–1013, DOI:10.1016/j.procs.2012.04.108. |
| [] | Li X L, Shen X S, Peng X D, et al. 2013. An accurate multimoment constrained finite volume transport model on Yin-Yang grids[J]. Adv. Atmos. Sci., 30(5): 1320–1330, DOI:10.1007/s00376-013-2217-x. |
| [] | McDonald A, Bates J R. 2009. Semi-Lagrangian integration of a gridpoint shallow water model on the sphere[J]. Mon. Wea. Rev., 117(1): 130–137, DOI:10.1175/1520-0493(1989)117<0130:SLIOAG>2.0.CO;2. |
| [] | Nair R, Côté J, Staniforth A. 1999. Cascade interpolation for semi-Lagrangian advection over the sphere[J]. Quart. J. Roy. Meteor. Soc., 125(556): 1445–1468, DOI:10.1002/qj.1999.49712555617. |
| [] | Peng X D, Xiao F, Takahashi K. 2006. Conservative constraint for a quasi-uniform overset grid on the sphere[J]. Quart. J. Roy. Meteor. Soc., 132(616): 979–996, DOI:10.1256/qj.05.18. |
| [] | Qaddouri A. 2011. Nonlinear shallow-water equations on the Yin-Yang grid[J]. Quart. J. Roy. Meteor. Soc., 137(656): 810–818, DOI:10.1002/qj.792. |
| [] | Qaddouri A, Laayouni L, Loisel S, et al. 2008. Optimized Schwarz methods with an overset grid for the shallow-water equations:Preliminary results[J]. Appl. Numer. Math., 58(4): 459–471, DOI:10.1016/j.apnum.2007.01.015. |
| [] | Qaddouri A, Lee V. 2011. The Canadian global environmental multiscale model on the Yin-Yang grid system[J]. Quart. J. Roy. Meteor. Soc., 137(660): 1913–1926, DOI:10.1002/qj.873. |
| [] | Williamson D L, Drake J B, Hack J J, et al. 1992. A standard test set for numerical approximations to the shallow water equations in spherical geometry[J]. J. Comput. Phys., 101(1): 211–224, DOI:10.1016/0021-9991(92)90060-C. |
| [] | Xiao F, Yabe T, Peng X D, et al. 2002. Conservative and oscillation-less atmospheric transport schemes based on rational functions[J]. J. Geophys. Res., 107(D22): ACL 2-1–ACL 2-11, DOI:10.1029/2001JD001532. |
| [] | Zerroukat M, Allen T. 2015. On the monotonic and conservative transport on overset/Yin-Yang grids[J]. J. Comput. Phys., 302: 285–299, DOI:10.1016/j.jcp.2015.09.006. |
 2017, Vol. 41
2017, Vol. 41