2 Division of Atmospheric Science, Desert Research Institute, NV Reno 89512
3 安徽省人工影响天气办公室, 合肥 230031
2 Division of Atmospheric Science, Desert Research Institute, NV Reno 89512
3 Weather Modification Office of Anhui Province, Hefei 230031
雨滴谱反映了单位体积一定粒径范围内雨滴粒子数浓度随尺度的变化趋势。由雨滴谱分布可以计算相应降水过程中的各种微物理特征量,如雨滴数浓度、平均粒径、降水强度、雷达反射率因子、液态水含量等。雨滴谱研究往往针对降水微物理过程,对提高雷达定量估测降水的精度,改进和优化气候模式中的降水参数化方案有重要意义(Gilmore et al., 2004; Krishna et al., 2016),并且可以指导人工增雨作业,定量估计作业效果,促进人工影响降水工作的发展等。
由于气候、大气状况以及地形条件的差异,雨滴谱分布呈现出明显的时空变化。鉴于此,国内外开展了很多关于不同地区、不同季节雨滴谱的观测研究(Tokay and Short, 1996;周毓荃等,2001)。Bringi et al.(2003)采用雷达和雨滴谱仪数据对不同气候区域的雨滴谱分布进行对比分析,发现对流性降水谱有明显的海陆差异,Ulbrich and Atlas(2007)对热带海洋性和大陆性对流系统的研究也得到了相同的结论。Islam et al.(2012)分析英国近七年的雨滴谱资料,证实了雨滴谱分布会随大气温度、湿度条件而变化。另外,受到降水形成机制的影响,对流云降水谱和层状云降水谱也有明显的不同(宫福久等,2007;Chen et al., 2013;柳臣中等,2015)。以上提到的都是关于雨滴谱的地面观测,为了使雨滴谱研究更好地服务于雷达测量和模式改进,就需要深入了解降水发展演变的微物理过程,这就使雨滴谱随高度变化的研究显得尤为重要。陈聪等(2015)结合2011年黄山地区一次积层混合云降水中三个不同高度的雨滴谱资料,分析了各高度雨滴谱的分布特征,发现雨滴的各尺度参量均在山腰最大,山底次之,山顶最小。杨俊梅等(2016)对山西省6个地区的雨滴谱进行了统计分析,发现对于层状云和对流云降水,山区降水的广义截距参数Nw和质量加权平均直径Dm均大于平原地区。张欢等(2013)对比分析庐山一次对流云降水中不同高度处的雨滴谱分布,认为在雨滴下落过程中,蒸发作用可以减少小雨滴和较大雨滴的数浓度,而使中等大小雨滴的数浓度增加。Geoffroy et al.(2014)结合飞机观测分析浅薄积云降水的雨滴谱,认为随着高度的降低,受到碰并、蒸发和沉降过程中尺度分选的共同影响,雨滴总数浓度减小而平均体积直径增加,同时单位面积上的雨滴数浓度通量随高度下降而减小。Rao et al.(2006)结合雨滴谱仪、雷达和风廓线仪数据,研究不同高度上雨滴谱的Gamma函数拟合,发现μ–Λ关系随海拔高度有明显的变化,并认为这一变化主要与雨滴的蒸发和破碎有关。
之前对雨滴谱随高度演变的研究多集中于个例或某类云系下雨滴谱的分析,对不同云系雨滴谱垂直演变的对比研究较少,且这些研究的观测数据来源于不同的气候区域,对比结果还会受到很多其他因素的影响。本次实验依托高山(黄山)对雨滴谱进行观测,可以较容易地得到同一区域不同海拔高度的雨滴谱数据,有助于更好地理解层状云降水云系和对流云降水云系下雨滴谱的廓线变化,为进一步研究降水的形成演变机制奠定基础。
2 实验设计与采样概况 2.1 观测时间与地点本文中,雨滴相关的观测数据来源于2011年6月4日至7月26日在安徽黄山地区三个不同高度的连续观测,实验仪器分别架设在光明顶气象站(海拔1860 m,30°08′N,118°09′E)、半山寺景点(海拔1351 m,30°07′N,118°10′E)和寨西人工影响天气示范基地(海拔464 m,30°03′N,118°09′E)。三个观测点海拔高度相差1400 m左右,水平距离不超过9 km,观测数据可以反映同一降水系统控制时不同高度的谱分布情况。
2.2 观测仪器与数据处理本次实验采用德国OTT公司生产的PARSIVEL粒子谱仪对雨滴谱进行测量,它是以激光测量为基础的粒子测量传感器。该仪器可以产生一个水平面积为54 cm2的激光束,降水粒子经过观测区域时会造成信号的衰减,由信号的衰减程度确定粒子的尺度,由穿越时间记录粒子的下落速度。仪器测量的粒子直径范围为0.2~25 mm,落速范围为0.2~20 m s−1,尺度和速度测量均分为32个非等间距的测量通道。此次观测的采样时间间隔选为10 s和60 s。
PARSIVEL在观测中对雨滴进行了球形假设,而大雨滴在下落过程中会有明显的形变,因此需要对雨滴尺度进行订正。本文采用Battaglia et al.(2010)的轴比订正法:假设直径D≤1 mm的雨滴没有形变,轴比为1;1 mm < D≤5 mm的雨滴轴比在0.7~1之间线性变化;D>5 mm时轴比为0.7。另外,对观测数据还进行了以下的质量控制:(1)剔除前两个尺度档和订正后雨滴直径大于8 mm的观测数据;(2)剔除粒子下落速度与Atlas et al.(1973)的经典下落速度相差大于5 m s−1的数据。
为对雨滴谱谱型及分布函数进行分析,需要将观测数据转换为单位体积、单位尺度间隔内的雨滴数浓度:
| $ N\left({{D_i}} \right) = \sum\limits_{j = 1}^{32} {\frac{{{n_{ij}}}}{{A \cdot \Delta t \cdot {V_j} \cdot \Delta {D_i}}}}, $ | (1) |
式中,nij表示直径位于第i个尺度区间内同时下落速度介于第j个速度区间的雨滴数,A(单位:m2)是仪器的采样面积,Δt(单位:s)是采样时间间隔,Di(单位:mm)和ΔDi(单位:mm)分别表示第i个尺度区间的中心直径和该区间的尺度间隔,Vj(单位:m s−1)表示第j个速度区间的中心速度。N(Di)(单位:mm−1 m−3)表示直径介于Di与Di+ΔDi的单位体积单位尺度间隔内的雨滴数。
根据雨滴谱数据可以得到部分微物理特征量,其中降水强度R(单位:mm h−1)和雨水含量W(单位:g m−3)的计算公式为
| $ R = \frac{{6{\rm{ \mathsf{ π} }}}}{{1{0^4}}}\sum\limits_{i = 3}^{24} {\sum\limits_{j = 1}^{32} {{V_j}N\left({{D_i}} \right)} } D_i^3\Delta {D_i}, $ | (2) |
| $ W = \frac{{{\rm{ \mathsf{ π} }}{\rho _{\rm{w}}}}}{{6000}}\sum\limits_{i = 3}^{24} {N\left({{D_i}} \right)D_i^3\Delta {D_i}}, $ | (3) |
其中ρw表示水的密度,为1.0 g cm−3。
研究表明(Niu et al.,2010),对于层状云和对流云降水的雨滴谱,Gamma函数的拟合效果都优于M-P函数,因此本文选用有三个可变参数的Gamma函数对雨滴谱进行拟合:
| $ N(D) = {N_0}{D^\mu }\exp(- \mathit{\Lambda }D), $ | (4) |
式中,D(单位:mm)是雨滴直径,N0(单位:mm−1−μ m−3)是截距参数,μ是形状因子,Λ(单位:mm−1)是斜率参数,此处采用阶距法对这三个参数进行计算,对于Gamma分布,雨滴谱的n阶距Mn为
| $ {M_n} = \int_0^\infty {{D^n}N(D)} {\rm{d}}D = {N_0}\frac{{\Gamma (\mu + n + 1)}}{{{\mathit{\Lambda }^{\mu + n + 1}}}}, $ | (5) |
为使拟合方法能用于模式中多参数微物理方案的改进,选用的三个阶距中必须包含0、3两个阶数,另外考虑到高阶距的计算会引入较大的误差,而太低阶距的计算又会带来大量的不确定性(Kumar er al, 2011),选择雨滴谱的4阶距作为第三个拟合参量。
在求解其他物理量的过程中,利用雨滴谱的3、4阶距,雨滴的质量加权平均直径Dm(单位:mm)可以表示为
| $ {D_{\rm{m}}} = \frac{{{M_4}}}{{{M_3}}}. $ | (6) |
根据Testud et al.(2001)的推导,由雨水含量W和质量加权平均直径Dm计算广义截距参数Nw(单位:mm−1 m−3):
| $ {N_{\rm{w}}} = \frac{{{4^4}}}{{{\rm{ \mathsf{ π} }}{\rho _{\rm{w}}}}}\left({\frac{{1{0^3}W}}{{D_{\rm{m}}^4}}} \right), $ | (7) |
式中ρw为水的密度,其值为1.0 g cm−3。广义截距参数相对于N0而言,不受到雨滴谱形(μ)的影响,可以反映雨水含量和雨滴尺度一定时,雨滴数浓度的大小情况,有更明确的物理意义(Testud et al., 2001)。
2.3 降水个例的选取及其概况在经过质量处理的数据中挑选降水个例。这里对一次降水事件的定义参考Tokay and Bashor(2010)的基于雨滴谱数据的方法。首先对时间分辨率为10 s的观测数据进行分钟求和,采样时间为60 s的数据可以直接应用。对于每一分钟的数据,当仪器输出的雨滴总个数≥10,同时降水强度R≥0.1 mm h−1时视为一个降水分钟,其余的均视为非降水数据。两个连续降水片段的间隔时间大于或等于1 h时分属于两次降水过程,最后将持续时间小于30 min的降水过程剔除。由此挑选出的降水个例山顶站为66个,山腰站76个,山底站64个。综合三个高度上各降水的开始时间和结束时间,挑选不同高度上时间相关性较好的11个例进行分析。
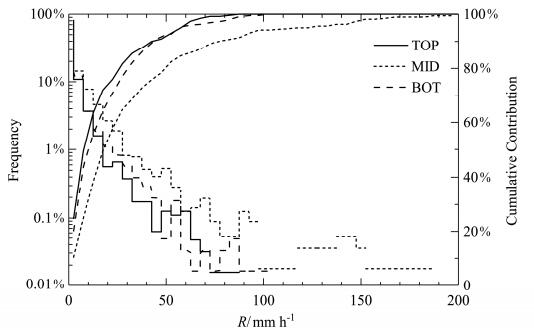
为了解所选个例的整体情况,对3个站点所有降水雨强的频率及其对总降水量的累积贡献进行分析,得到如图 1所示的分布图,图中TOP表示山顶,MID表示山腰,BOT表示山底。由图可见,分布频率随降水强度R的增加大体上呈减小趋势,除了降水强度R<5 mm h−1和R介于60~65 mm h−1的区间外,其余强度降水发生的频率均在山腰处最大,雨强>110 mm h−1的降水仅出现在山腰。R<5 mm h−1的降水发生的频数在山顶为81%,山腰为64%,山底为79%,该强度区间内降水对总降水量的贡献分别为:山顶25%、山腰10%、山底20%,可见相对于山腰和山底,弱降水在山顶处出现的频率更高,比例更大。与弱降水相比,R>10 mm h−1的降水发生的频数很小(山顶:8%,山腰:22%,山底:9%)但对总降水量的贡献(山顶:51%,山腰:75%,山底:56%)却明显大于出现频率很高的弱降水。
|
图 1 山顶(TOP)、山腰(MID)和山底(BOT)各强度降水的频率分布(折线)及其对总降水量的累积贡献(曲线) Figure 1 Frequency distributions (fold lines) and cumulative contributions to total rainfall (curves) of precipitation with different intensity on the mountaintop (TOP), mountainside (MID), and mountain bottom (BOT) |
不同类型降水的雨滴谱分布有较大的差异,因此有必要对不同降水云系的雨滴谱进行分类分析,通常情况下将降水分为两类:对流云降水和层状云降水(刘红燕和雷恒池,2006;胡子浩等,2013;Tang et al.,2014)。已有研究(Tokay and Short, 1996)表明,两类降水相互转换时截距参数N0的值会发生突变,且此时对应的降水强度约为5.5 mm h−1。选取黄山观测点一次持续时间较长的降水个例进行验证,发现N0值发生突变时对应的R在5 mm h−1左右。同时相对于对流云而言,层状云通常水平延伸范围更广,降水强度较弱(Marzano et al., 2010)。因此结合Chen et al.(2013)的分类方法,以雨滴谱数据为基础对观测点的降水类型进行划分:对于某一瞬时时刻ti,若从ti-Ns到ti+Ns这段时间内,降水强度R均>0.5 mm h−1,同时其标准差<1.5 mm h−1,则将ti时刻的降水视为层状云降水;若从ti-Ns到ti+Ns这段时间内,降水强度R均>5 mm h−1,同时其标准差大于1.5 mm h−1,则将该时刻的降水视为对流云降水,此处将Ns取为5个样本。既不属于层状云降水也不属于对流云降水的,就视为混合性降水,陈聪等(2015)已对其进行过个例研究,这里不再讨论。
表 1给出了三个高度上11个个例的雨滴谱样本总数及层状云和对流云降水的样本数,括号中是各类样本在总样本中所占的比例。由表 1可见山顶和山底层状云降水样本数明显多于对流云降水样本数,两站点层状云样本占总样本的比例很相近,都在29%左右,而对流云样本占比仅为9%~12%。山腰两类降水粒子谱样本数相当,层状云和对流云降水粒子谱分别占总样本数的23%和22%。山顶、山腰和山底层状云降水强度的平均值分别为:3.00 mm h−1、3.75 mm h−1、3.39 mm h−1,对流云降水强度的平均值分别为:18.51 mm h−1、23.51 mm h−1、19.18 mm h−1,不管是对流云降水还是层状云降水,降水强度的平均值均在山腰最大,降水强度的差异直观地反映了雨滴谱分布的差异。
| 表 1 两类降水粒子谱的样本概况 Table 1 General features of raindrop spectra for two types of precipitation |
雨滴谱的微物理特征量可以很好地反映降水的基本特性,表 2给出了三个观测点、两类降水部分微物理参量的平均值。其中R为降水强度,Nt为总数浓度,D和Dm分别为雨滴的算术平均直径和质量加权平均直径,Dmax为雨滴的最大直径即谱宽,W为雨水含量,N1/Nt和R1/R分别为直径<1 mm的雨滴对雨滴总数浓度和总降水强度的贡献。
| 表 2 各高度降水粒子谱微物理特征量的平均值(S为层状云降水,C为对流云降水) Table 2 Average values of microphysical parameters for raindrop spectra at different altitudes (S is for stratiform precipitation, C is for convective precipitation) |
由表 2可见,对流云降水的雨滴尺度参数和数浓度都大于层状云降水,以山底为例,对流云降水的算术平均直径和质量加权平均直径分别为0.89 mm和1.47 mm,层状云为0.76 mm和1.19 mm;最大直径的平均值在对流云降水中为2.81 mm,层状云降水中为2.11 mm;对流云降水中雨滴总数浓度的平均值为707.75 m−3,层状云为272.81 m−3。对流云降水较大的雨滴尺度和较高的数浓度导致其雨水含量和降水强度明显大于层状云降水,三个高度上对流云的雨水含量均在层状云的5倍左右,而降水强度则达到了层状云降水强度的6倍左右。直径<1 mm的雨滴对总数浓度的贡献(N1/Nt)在层状云降水中介于74%~83%,在对流云降水中该比例较低为61%~72%,可见雨滴数浓度主要来源于小粒径段的贡献,且层状云降水中小雨滴的数浓度占比更高。但直径<1 mm的雨滴对总降水强度的贡献(R1/R)却较小,尤其是在山腰地区的对流云降水中,仅为7.90%。不管是层状云降水还是对流云降水,山顶处N1/Nt和R1/R的值均大于山腰和山底,结合Zwiebel et al.(2016)的分析,认为可能是由于山顶海拔高度较高,雨滴出云后经历的下落距离较短,碰并作用对雨滴谱演变的影响较山腰和山底的小,因此山顶处小雨滴数较多。对比不同高度的雨滴尺度可以发现,层状云降水和对流云降水中,雨滴的各尺度参量均是山腰>山底>山顶。而陈聪等(2015)对黄山地区一次积层混合云过程的研究也得到了相同的结论,说明受到地形及观测点与云底相对位置的影响,黄山地区各类降水的雨滴尺度都是山顶最小,山腰最大。
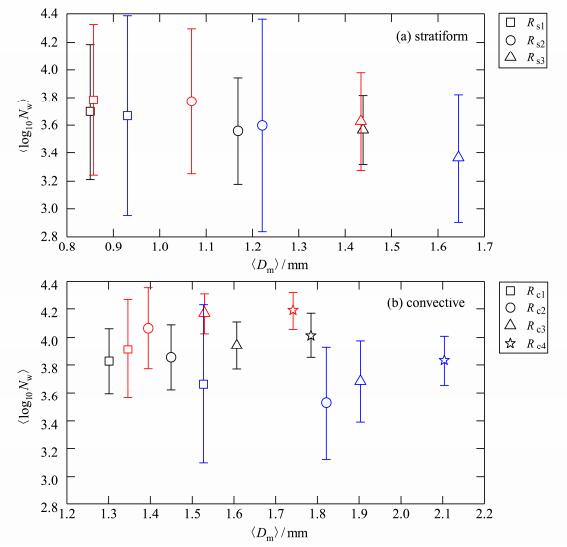
3.2 质量加权平均直径Dm和广义截距参数Nw随降水强度的分布微物理参量中的截距参数和特征尺度还可以反映降水的形成和演变机制(Bringi et al.,2003)。图 2是三个高度两类降水不同降水强度区间对应的〈Dm〉和〈log10Nw〉关系图,其中尖括号代表平均值,图中同时给出了截距参数Nw的标准差。由于对流云和层状云降水强度差异较大,故分别选取不同的划分区间:层状云降水强度区间分别为0.5<Rs1≤1,1<Rs2≤5,Rs3>5;对流云降水强度区间分别为5<Rc1≤10,10<Rc2≤20,20<Rc3≤40,Rc4>40,降水强度的单位是mm h−1。由图 2可见,随降水强度R的增加,质量加权平均直径Dm逐渐增大,而广义截距参数Nw没有明显的变化趋势,说明降水强度的增加主要源于雨滴尺度的增大。同一降水强度区间内山腰处的Dm大于山顶和山底,以对流云降水为例,山腰〈Dm〉的变化范围为:1.53~2.10 mm,山顶为:1.35~1.74 mm,山底为:1.30~1.78 mm。另外在强度较大的层状云降水和对流云降水中,山腰〈log10Nw〉小于山顶和山底,说明在降水强度较大时,山腰雨滴尺度较大而浓度较低。
|
图 2 各观测点Dm和log10Nw平均值的关系随降水强度的变化(图中红色表示山顶、蓝色表示山腰、黑色表示山底;正方形,空心圆,三角形,星形标记分别代表不同的降水强度区间) Figure 2 Variations of the relations between averaged Dm and log10Nw with rainfall intensity (Red bar represents mountaintop, blue bar represents mountainside, and the black represents mountain bottom; square, hollow circle, triangle and star markers represent different rain intensity) |
另外,已有研究表明雨滴尺度和数浓度参数的变化范围会随降水强度而变(Kumar et al.,2011;Chen et al.,2013)。Islam et al.(2012)结合英国南部奇尔波顿气象台近七年的雨滴谱数据,分析不同季节和湿度条件下的雨滴谱特征,发现log10Nw的变化范围随质量加权平均直径Dm即降水强度的增加而减小,并且在强降水中由于雨滴间的碰并和破碎作用达到平衡,Dm也达到一个平衡值。由本文的观测数据也可以得到相似的结论,由图 2可见,多数情况下弱降水对应的log10Nw的变化范围较大,随降水强度R的增加,雨滴谱演变趋于稳定,log10Nw的变化范围逐渐减小。考察雨滴谱log10Nw的标准差在各降水强度区间内的数值(表 3),可以发现除山腰Rs1~Rs2区间外,其余情况下log10Nw的标准差都是随降水强度的增加而减小的。
| 表 3 三个高度各降水强度区间对应的log10Nw的标准差 Table 3 Standard deviations of log10Nw corresponding to different rain types and intensities at three altitudes |
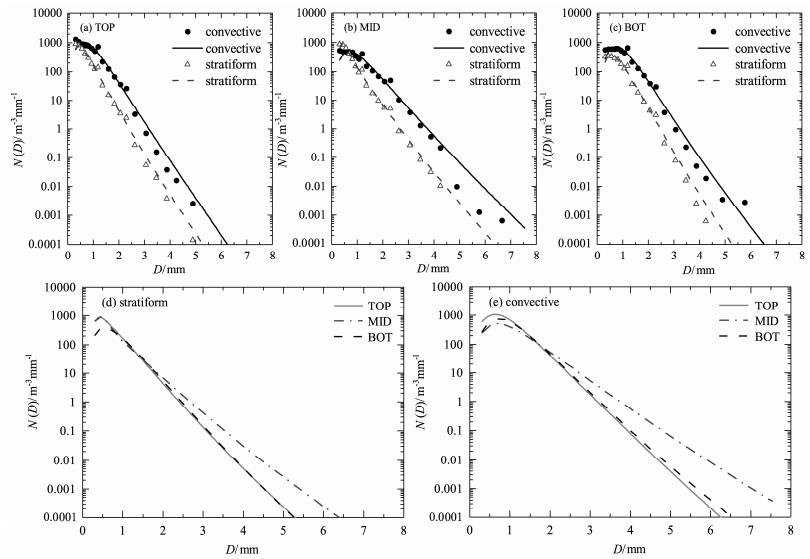
描述雨滴谱分布的解析函数在降水的遥感探测及模式参数化方案中有广泛的应用,并且其拟合参数与观测的时间、地点、降水类型、观测点的气候条件等有关(Tang et al., 2014)。雨滴谱拟合中最常用的是M−P分布和Gamma分布,其中Gamma分布由于形状参数μ的引入,拟合效果通常会优于M-P分布(Niu et al., 2010; 张昊等,2011)。图 3是不同降水类型和不同海拔高度下雨滴谱分布的对比图,其中图 3a、b、c分别为山顶、山腰和山底位置处层状云降水粒子谱和对流云降水粒子谱的对比,图中散点代表观测平均值,曲线是Gamma函数拟合的结果;图 3d、e分别为层状云降水和对流云降水中不同高度Gamma函数拟合谱的对比。
|
图 3 雨滴谱分布在(a、b、c)不同降水类型和(d、e)不同海拔高度下的对比。(a)中实线和虚线分别代表山顶对流云降水谱和层状云降水谱的Gamma拟合,圆点和三角形分别代表对流云降水和层状云降水的观测平均谱,(b、c)是山腰和山底的谱分布,其余同(a);(d)中实线、点划线和虚线分别代表山顶、山腰和山底层状云降水谱的Gamma拟合,(e)是相对于对流云降水谱的Gamma拟合,其余同(d) Figure 3 Comparison of raindrop spectra between (a, b, c) different rain types and (d, e) different altitudes. Solid and dashed lines in (a) represent Gamma fitting of spectra for convective and stratiform precipitation on mountaintop, dots and triangles represent the mean values of observations for convective and stratiform precipitation respectively, while (b, c) is for mountainside and mountain bottom with others are same as (a); the solid, dash-dotted and dashed lines in (d) show the Gamma fitting of startiform rainfall spectra for mountaintop, mountainside and mountain bottom, (e) is for convective precipitation with others are same as (d) |
由图可见,三个高度上对流云降水和层状云降水的雨滴谱谱型相似,峰值直径都<1 mm,但对流云降水粒子谱的峰值直径略大于相同高度上层状云降水粒子谱的峰值直径。山顶和山底对流云降水粒子谱的峰值浓度大于层状云,山腰则相反。除山腰站观测到的直径小于0.6 mm的雨滴外,其他尺度雨滴的数浓度在三个高度都是对流云降水的高于层状云降水的。从拟合效果来看,三个高度上的雨滴谱都比较符合Gamma分布。图 3d、e是关于不同高度雨滴谱的对比,由图可见层状云降水山顶和山腰的雨滴谱峰值浓度很接近,分别为928.51 m−3 mm−1和884.90 m−3 mm−1,均大于山底的峰值浓度,对流云降水中峰值浓度是山顶>山底>山腰,而陈聪等(2015)的研究表明黄山积层混合云降水中雨滴谱的峰值浓度是山顶>山腰>山底,由此可见,不同降水云系下的雨滴谱随高度有不同的演变特征。不管是层状云降水还是对流云降水,山腰处直径>2 mm的雨滴的数浓度都大于山顶和山底,但由于小粒径端对数浓度的贡献较大,结合表 2中对雨滴总数浓度的分析可见,不同高度总数浓度的大小关系与峰值浓度的大小关系一致。
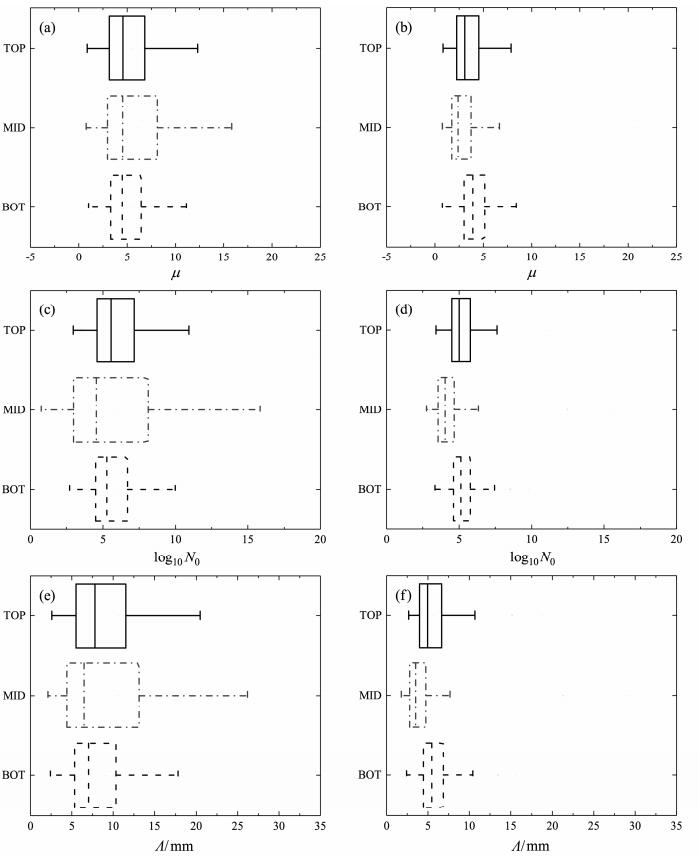
雨滴谱Gamma函数拟合的三参数N0,μ,Λ在半对数坐标系中分别是拟合曲线的截距、形状因子和斜率,由拟合参数的变化分析雨滴谱的演变,可以代表雨滴谱变化的平均状况,减少常规观测数据分析中的误差(Feingold and Levin, 1986)。图 4是Gamma拟合三参数随高度变化的箱线图,其中图 4a、c、e对应于层状云降水,图 4b、d、f对应于对流云降水。
|
图 4 雨滴谱拟合参数随高度的变化:(a、c、e)分别对应于层状云降水中μ,log10N0,Λ的分布情况;(b、d、f)分别对应于对流云降水中μ,log10N0,Λ的分布情况 Figure 4 Variation of fitting parameters for raindrop spectra with altitude: (a, c, e) Distributions of μ, log10N0, and Λ for stratiform precipitation; (b, d, f) distributions of μ, log10N0, and Λ for convective precipitation |
由图可见,相对于对流云降水,层状云降水粒子谱的三个参数随高度的变化比较小,说明不同海拔高度层状云降水粒子谱的差异较小,而对流云降水粒子谱随高度有明显的变化。Tang et al.(2014)对比分析北京、张北和阳江三个不同区域的雨滴谱,发现三个观测点层状云降水粒子谱的差异小于对流云降水粒子谱的差异,此处数据说明不同高度上的谱差异亦是如此。并且由图 4b、d、f可以明显看出对流云降水粒子谱三个参数的各分位数以及平均值都是在山腰处最小。已有研究表明,形状因子μ和斜率参数Λ与雨滴谱的宽度成反相关关系(Geoffroy et al., 2014),而N0可以在一定程度上反映雨滴谱峰值浓度的大小,所以由拟合参数的分布情况可知对流云降水中山腰处雨滴峰值浓度最小而谱宽最大,这与图 3e显示的结果是一致的。由图中还可以发现,相对于对流云降水,相同高度上层状云降水粒子谱参数的变化范围较大,而由Kumar et al.(2011)的研究可知雨滴谱拟合三参数的变化范围随降水强度的增加而减小,所以层状云较小的降水强度可能是导致其雨滴谱参数变化较大的原因。
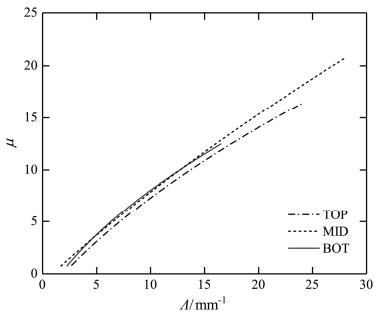
3.4 μ–Λ关系Gamma函数拟合的三参数并不是完全独立的,很多研究(Ulbrich,1983;Zhang et al., 2003)表明斜率参数Λ和形状因子μ有较好的相关性。分析μ–Λ关系可以将三参数的Gamma分布简化为双参,对雷达定量测量降水有重要意义。图 5给出了山顶、山腰和山底μ–Λ关系的拟合曲线。由于弱降水中雨滴谱的观测误差和统计变化都较大,故采用Chen et al.(2013)的数据筛选标准,本文在拟合μ–Λ关系时,仅挑选了对流云降水中雨滴总数大于1000的样本,各高度满足筛选条件的样本数足够多(山顶:327,山腰:389,山底:309),保证了分析结果的可靠性。表 4给出了三个高度μ–Λ关系的拟合系数。由图可见,山腰和山底的拟合曲线很相近,对于给定的Λ,山顶μ值略小于山腰和山底。Ulbrich(1983)的研究表明,满足Gamma分布的雨滴谱,μ–Λ关系也可以表示为ΛDm=4+μ,式中Dm为雨滴的质量加权平均直径,说明μ–Λ拟合曲线的差异与雨滴尺度的不同有关,并且在斜率参数Λ相同的情况下,μ越小相应谱的雨滴尺度也越小,由该拟合结果同样可以得到山顶雨滴平均尺度较小的结论。以上分析表明受到雨滴尺度的影响,雨滴谱的μ–Λ关系会随海拔高度变化,因此为提高雷达反演降水的准确性,有必要对不同海拔高度的雨滴谱及其μ–Λ关系进行分析。
|
图 5 三个高度对流云降水μ–Λ关系的拟合曲线 Figure 5 Fitted μ–Λ relations for convective precipitation at three different altitudes |
| 表 4 三个高度对流云降水μ–Λ关系的拟合系数 Table 4 Coefficients of the fitted μ–Λ relations for convective precipitations at three different altitudes |
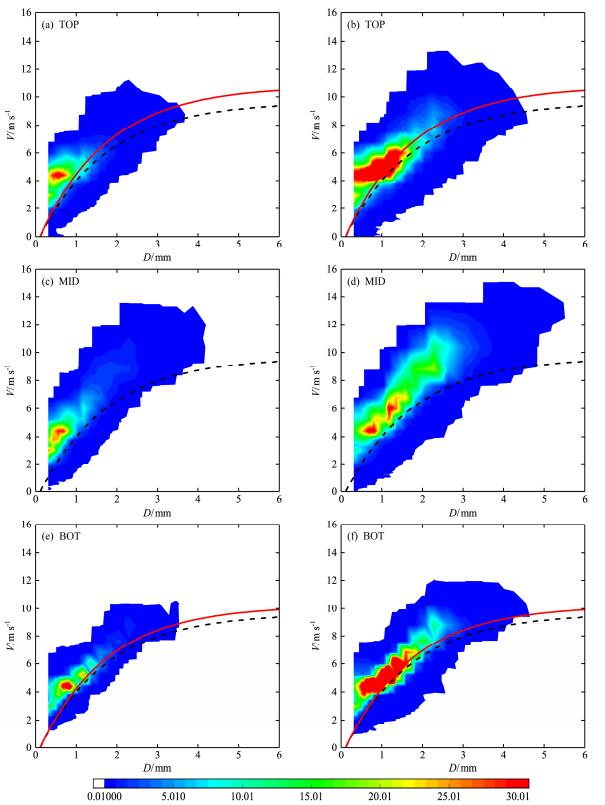
PARSIVEL雨滴谱仪可以同时测量雨滴的尺度和落速,图 6给出了观测得到的雨滴数随直径和下落速度的分布情况,其中图 6a、c、e分别对应于山顶、山腰和山底的层状云降水,图 6b、d、f对应于同高度的对流云降水。图中同时叠加了Atlas et al.(1973)基于Gunn and Kinzer(1949)测量实验中得到的标况下雨滴下落末速的拟合曲线(黑色虚线),山顶和山底还给出了考虑空气密度影响后的订正曲线(红色实线)。
|
图 6 观测得到的雨滴数随直径和下落速度的分布:(a、c、e)分别对应于山顶、山腰、山底的层状云降水;(b、d、f)分别对应于山顶、山腰、山底的对流云降水。黑色虚线:标况下下落末速的拟合曲线;红色实线:考虑空气密度影响后的订正曲线 Figure 6 Observed number of raindrops as a function of the drop diameter and falling velocity: (a, c, e) Stratiform and (b, d, f) convective precipitation for mountain top, mountainside and mountain bottom. Black dotted line: terminal speed under the standard condition; red solid line: corrected curve considering the effect of air density |
由图可见,各尺度雨滴都对应于一个落速范围,而非一个固定的速度值,并且对流云降水中的落速范围略大于相同位置上的层状云降水,说明雨滴的落速不仅受到尺度的影响,还与其它很多因素有关。层状云降水粒子的下落速度多集中于3~5 m s−1,而对流云降水粒子的下落速度多为3~7 m s−1,观测平均的雨滴数极值均位于Atlas速度曲线的上方。Atlas速度曲线拟合的是标况下海平面高度雨滴的下落末速,对应的空气密度为1.23 kg m−3,而本次实验三个观测点的海拔高度均高于海平面,其中山顶和山底的平均气压分别为812.5 hPa和952.8 hPa,平均空气密度为0.98 kg m−3、1.12 kg m−3。考虑空气密度对下落速度V(单位:m s-1)的影响,采用Atlas et al.(1973)给出的订正因子,在标况公式的右侧乘以(ρ0/ρ)0.4,即
| $ V = (9.65 - 10.3{{\rm e}^{ - 0.6D}}){({{{\rho _0}} \mathord{\left/ {\vphantom {{{\rho _0}} \rho }} \right. } \rho })^{0.4}}, $ | (8) |
其中,ρ0是海平面的空气密度,ρ是观测点空气密度的平均值,订正结果(红色实线)在山顶和山底的分布图中都有给出,订正后的曲线更接近于实际观测值,说明黄山观测点较低的空气密度是导致观测速度高于其下落末速的原因之一。
但订正曲线与实际观测的雨滴落速仍有一定的偏差,尤其是在小尺度端。图 7给出了山顶和山底

|
图 7 山顶和山底落速偏差随雨滴尺度的变化,其中v(D)为观测的雨滴落速的加权平均值(以雨滴数为权重),vt(D)是经过密度订正后的下落末速度 Figure 7 Dependence of velocity deviations on the raindrop diameter on mountaintop and mountain bottom. v(D) represents weighted average of observed velocity (weighted by the number of raindrops) while vt(D) is the corrected value of terminal speed by air density |
本研究利用2011年6月4日至7月26日在黄山不同高度的雨滴谱观测资料,对比分析三个观测点对流云降水和层状云降水雨滴谱的微物理特征量、Gamma函数拟合以及雨滴下落速度的分布情况,得到以下几点结论:
(1)三个高度上对流云降水的雨水含量和降水强度、雨滴的各类尺度参数和数浓度都比相同位置上层状云降水的大;对于不同海拔高度的对比而言,两类降水的雨滴尺度均是在山腰处最大,山底次之,山顶最小;随降水强度R的增加,雨滴的质量加权平均直径Dm逐渐增大,广义截距参数(log10Nw)的标准差逐渐减小。
(2)Gamma函数可以较好地拟合采样点雨滴谱的分布情况,由拟合参数分析雨滴谱的演变,发现相对于对流云降水,层状云降水粒子谱随高度的变化较小;Gamma函数中的斜率参数Λ和形状因子μ有较好的相关性,可以用二项式进行拟合,拟合结果与观测点所处的区域和海拔高度有关。
(3)各尺度雨滴的下落速度都有一定的变化,且对流云降水中的变化范围略大于相同位置上的层状云降水。空气的垂直运动、雨滴的碰并破碎、湍流运动以及仪器误差等都会导致实际雨滴的下落速度偏离其理论下落末速度。
本文的研究证明雨滴谱随降水类型和海拔高度有明显的变化,分析不同降水类型和高度下的雨滴谱分布情况对于提高雷达定量估测降水的精度、改进模式中的降水参数化方案有重要意义。雨滴谱的演变主要与下落过程中经历的一系列微物理过程有关,但仅由观测数据无法得到各微物理机制对雨滴谱演变的影响,今后的研究将借助模式手段对其进行进一步分析。
Atlas D, Srivastava R C, Sekhon R S. 1973. Doppler radar characteristics of precipitation at vertical incidence [J]. Rev. Geophys., 11(1): 1-35. DOI:10.1029/RG011i001p00001
|
Battaglia A, Rustemeier E, Tokay A, et al. 2010. PARSIVEL snow observations:A critical assessment [J]. J. Atmos. Oceanic Technol., 27(2): 333-344. DOI:10.1175/2009JTECHA1332.1
|
Battan L J. 1964. Some observations of vertical velocities and precipitation sizes in a thunderstorm [J]. J. Appl. Meteor., 3(4): 415-420. DOI:10.1175/1520-0450(1964)003<0415:SOOVVA>2.0.CO;2
|
Bringi V N, Chandrasekar V, Hubbert J, et al. 2003. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis [J]. J. Atmos. Sci., 60(2): 354-365. DOI:10.1175/1520-0469(2003)060<0354:RSDIDC>2.0.CO;2
|
Chen B J, Yang J, Pu J P. 2013. Statistical characteristics of raindrop size distribution in the Meiyu season observed in eastern China [J]. J. Meteor. Soc. Japan, 91(2): 215-227. DOI:10.2151/jmsj.2013-208
|
陈聪, 银燕, 陈宝君. 2015. 黄山不同高度雨滴谱的演变特征[J]. 大气科学学报, 38(3): 388-395. Chen C, Yin Y, Chen B J. 2015. Raindrop size distribution at different altitudes in Mt.Huang (in Chinese)[J]. Trans. Atmos. Sci, 38(3): 388-395.
|
Feingold G, Levin Z. 1986. The lognormal fit to raindrop spectra from frontal convective clouds in Israel [J]. J. Climate Appl. Meteor., 25(10): 1346-1363. DOI:10.1175/1520-0450(1986)025<1346:TLFTRS>2.0.CO;2
|
Geoffroy O, Siebesma A P, Burnet F. 2014. Characteristics of the raindrop distributions in RICO shallow cumulus [J]. Atmos. Chem. Phys., 14(19): 10897-10909. DOI:10.5194/acp-14-10897-2014
|
Gilmore M S, Straka J M, Rasmussen E N. 2004. Precipitation uncertainty due to variations in precipitation particle parameters within a simple microphysics scheme [J]. Mon. Wea. Rev., 132(11): 2610-2627. DOI:10.1175/MWR2810.1
|
宫福久, 何友江, 王吉宏, 等. 2007. 东北冷涡天气系统的雨滴谱特征[J]. 气象科学, 27(4): 365-373. Gong F J, He Y J, Wang J H, et al. 2007. Characteristics of raindrop size distributions of northeast cold vortex precipitation in China (in Chinese)[J]. Sci. Meteor. Sinica (in Chinese), 27(4): 365-373. DOI:10.3969/j.issn.1009-0827.2007.04.002
|
Gunn R, Kinzer G D. 1949. The terminal velocity of fall for water droplets in stagnant air [J]. J. Meteor., 6(4): 243-248. DOI:10.1175/1520-0469(1949)006<0243:TTVOFF>2.0.CO;2
|
胡子浩, 濮江平, 张欢, 等. 2013. 庐山地区层状云和对流云降水特征对比分析[J]. 气象与环境科学, 36(4): 43-49. Hu Z H, Pu J P, Zhang H, et al. 2013. Characteristics comparison analysis of stratiform cloud and convective cloud precipitation in Lushan (in Chinese)[J]. Meteor. Environ. Sci. (in Chinese), 36(4): 43-49. DOI:10.3969/j.issn.1673-7148.2013.04.008
|
Islam T, Rico-Ramirez M A, Thurai M, et al. 2012. Characteristics of raindrop spectra as normalized gamma distribution from a Joss-Waldvogel disdrometer [J]. Atmos. Res., 108: 57-73. DOI:10.1016/j.atmosres.2012.01.013
|
Kinnell P I A. 1976. Some observations on the Joss-Waldvogel rainfall disdrometer [J]. J. Appl. Meteor., 15(5): 499-502. DOI:10.1175/1520-0450(1976)015<0499:SOOTJW>2.0.CO;2
|
Krishna U V M, Reddy K K, Seela B K, et al. 2016. Raindrop size distribution of easterly and westerly monsoon precipitation observed over Palau islands in the western Pacific Ocean [J]. Atmos. Res., 174-175: 41-51. DOI:10.1016/j.atmosres.2016.01.013
|
Kumar L S, Lee Y H, Ong J T. 2011. Two-parameter Gamma drop size distribution models for Singapore [J]. IEEE Trans. Geosci. Remote Sens., 49(9): 3371-3380. DOI:10.1109/TGRS.2011.2124464
|
柳臣中, 周筠珺, 谷娟, 等. 2015. 成都地区雨滴谱特征[J]. 应用气象学报, 26(1): 112-121. Liu C Z, Zhou Y J, Gu J, et al. 2015. Characteristics of raindrop size distribution in Chengdu (in Chinese)[J]. J. Appl. Meteor. Sci. (in Chinese), 26(1): 112-121. DOI:10.11898/1001-7313.20150112
|
刘红燕, 雷恒池. 2006. 基于地面雨滴谱资料分析层状云和对流云降水的特征[J]. 大气科学, 30(4): 693-702. Liu H Y, Lei H C. 2006. Characteristics of rain from stratiform versus convective cloud based on the surface raindrop data (in Chinese)[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 30(4): 693-702. DOI:10.3878/j.issn.1006-9895.2006.04.14
|
Marzano F S, Cimini D, Montopoli M. 2010. Investigating precipitation microphysics using ground-based microwave remote sensors and disdrometer data [J]. Atmos. Res., 97(4): 583-600. DOI:10.1016/j.atmosres.2010.03.019
|
Montero-Martínez G, Kostinski A B, Shaw R A, et al. 2009. Do all raindrops fall at terminal speed? [J]. Geophys. Res. Lett., 36(11): L11818. DOI:10.1029/2008GL037111
|
Niu S J, Jia X C, Sang J R, et al. 2010. Distributions of raindrop sizes and fall velocities in a semiarid plateau climate:Convective versus stratiform rains [J]. J. Appl. Meteor. Climatol., 49(4): 632-645. DOI:10.1175/2009JAMC2208.1
|
Rao T N, Kirankumar N V P, Radhakrishna B, et al. 2006. On the variability of the shape-slope parameter relations of the Gamma raindrop size distribution model [J]. Geophys. Res. Lett., 33(22): L22809. DOI:10.1029/2006GL028440
|
Tang Q, Xiao H, Guo C W, et al. 2014. Characteristics of the raindrop size distributions and their retrieved polarimetric radar parameters in northern and southern China [J]. Atmos. Res., 135-136: 59-75. DOI:10.1016/j.atmosres.2013.08.003
|
Testud J, Oury S, Black R A, et al. 2001. The concept of "normalized" distribution to describe raindrop spectra:A tool for cloud physics and cloud remote sensing [J]. J. Appl. Meteor., 40(6): 1118-1140. DOI:10.1175/1520-0450(2001)040<1118:TCONDT>2.0.CO;2
|
Tokay A, Short D A. 1996. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds [J]. J. Appl. Meteor., 35(3): 355-371. DOI:10.1175/1520-0450(1996)035<0355:EFTRSO>2.0.CO;2
|
Tokay A, Bashor P G. 2010. An experimental study of small-scale variability of raindrop size distribution [J]. J. Appl. Meteor. Climatol., 49(11): 2348-2365. DOI:10.1175/2010JAMC2269.1
|
Ulbrich C W. 1983. Natural variations in the analytical form of the raindrop size distribution [J]. J. Climate Appl. Meteor., 22(10): 1764-1775. DOI:10.1175/1520-0450(1983)022<1764:NVITAF>2.0.CO;2
|
Ulbrich C W, Atlas D. 2007. Microphysics of raindrop size spectra:Tropical continental and maritime storms [J]. J. Appl. Meteor. Climatol., 46(11): 1777-1791. DOI:10.1175/2007JAMC1649.1
|
杨俊梅, 陈宝君, 韩永翔, 等. 2016. 山西省不同地区雨滴谱的统计特征[J]. 气象科学, 36(1): 88-95. Yang J M, Chen B J, Han Y X, et al. 2016. Statistical characteristics of raindrop size distribution in different regions of Shanxi (in Chinese)[J]. J. Meteor. Sci. (in Chinese), 36(1): 88-95. DOI:10.3969/2014jms.0107
|
Zhang G F, Vivekanandan J, Brandes E A, et al. 2003. The shape-slope relation in observed Gamma raindrop size distributions:Statistical error or useful information? [J]. J. Atmos. Oceanic Technol., 20(8): 1106-1119. DOI:10.1175/1520-0426(2003)020<1106:TSRIOG>2.0.CO;2
|
张昊, 濮江平, 李靖, 等. 2011. 庐山地区不同海拔高度降水雨滴谱特征分析[J]. 气象与减灾研究, 34(2): 43-50. Zhang H, Pu J P, Li J, et al. 2011. Analysis of characteristics of raindrop size distribution at different altitudes in Lushan (in Chinese)[J]. Meteorology and Disaster Reduction Research (in Chinese), 34(2): 43-50. DOI:10.3969/j.issn.1007-9033.2011.02.007
|
张欢, 濮江平, 胡子浩, 等. 2013. 庐山不同高度雨滴谱分析[J]. 气象与环境科学, 36(2): 26-30. Zhang H, Pu J P, Hu Z H, et al. 2013. Analysis of raindrop spectrum at different altitudes in Lushan (in Chinese)[J]. Meteor. Environ. Sci. (in Chinese), 36(2): 26-30. DOI:10.3969/j.issn.1673-7148.2013.02.005
|
周毓荃, 刘晓天, 周非非, 等. 2001. 河南干旱年地面雨滴谱特征[J]. 应用气象学报, 12(S1): 39-47. Zhou Y Q, Liu X T, Zhou F F, et al. 2001. Characteristics of surface raindrop spectra in drought years in Henan Province (in Chinese)[J]. Quart. J. Appl. Meteor. Sci. (in Chinese), 12(S1): 39-47. DOI:10.3969/j.issn.1001-7313.2001.z1.006
|
Zwiebel J, Van Baelen J, Anquetin S, et al. 2016. Impacts of orography and rain intensity on rainfall structure. The case of the HyMeX IOP7a event [J]. Quart. J. Roy. Meteor. Soc., 142(S1): 310-319. DOI:10.1002/qj.2679
|
 2018, Vol. 42
2018, Vol. 42


