1 引言

我国位于东亚季风区，夏季热带天气系统活动异常活跃，是世界上台风登陆最多、受灾最重的国家之一，台风一旦在热带洋面上生成，其未来移动路径和发展变化就受到密切关注。探测技术的发展，资料同化和集合预报技术的应用，数值模式精度的提高及物理过程的完善，使得对大尺度环境气流引导下台风路径的预测能力不断提高（Xue et al., 2013; Huang et al., 2015）。而对路径突变（北翘、急转、回旋）的台风预测仍然面临诸多挑战，对路径突变的机理缺乏充分的了解。因此，加强对台风路径转折的研究，特别是不同因素在台风路径转折过程中的作用和贡献是一个重要的课题，具有重要的科学意义和实际应用价值，值得开展深入研究和探讨（陈联寿和孟智勇，2001）。

台风运动很大程度上受到外部不同尺度天气系统的影响，如副热带高压的进退与强弱，中高纬度槽脊调整以及低纬度季风槽位置变化都可能使台风转向、回旋、停滞或加速（Chan and Gray, 1982; 黄荣辉等，2016）。Harr and Elsberry（1991）发现强的副热带高压南侧的异常东风有利于台风直行，而强的季风槽和弱的副热带高压条件下异常的西风有利于台风转向。Shi et al.（2014）用位涡诊断方法和数值模拟了Megi台风北折的过程，发现中纬度的大陆高压和太平洋副热带高压的断裂以及低纬度的小尺度反气旋系统是造成其路径突变的原因。季风涡旋和台风的相互作用也能造成台风突然向北运动（Carr and Elsberry, 1995）。Liang and Wu（2015）发现了台风路径对季风涡旋初始时的风廓线较为敏感。

在正压框架下，台风的运动主要受到引导气流和β效应的共同作用（Holland, 1983; Chan and Williams, 1987; Fiorino and Elsberry, 1989; Smith et al., 1990; Willoughby, 1990, 1992; Holland and Lander, 1993; 王斌等，1998）。表面摩擦、地形、海温变化、台风和海洋的相互作用等外源强迫作用都可以在一定条件下显著地影响台风的运动（Chang, 1982; Yeh and Elsberry, 1993a, 1993b）。罗哲贤和陈联寿（1995）用β平面准地转正压模式研究台湾岛地形对台风移动路径的作用，发现台湾岛地形会使台风路径向右偏移。钟水新等（2014）在中国南海台风模式中发展和引进了地形重力波拖曳参数化方案后，模式对台风登陆时路径和强度的预报能力均有提高。事实上台风移动路径是上述外部和内部过程共同作用的结果（Luo et al., 2011），环境场的垂直风切变和台风内部非绝热加热引起的斜压效应是造成台风转向的原因（Shapiro, 1992; Wu and Emanuel, 1993; Wang and Holland, 1996）。台风内部中小尺度对流系统在眼墙上的非均匀的发展，改变了台风眼区及内部热力和动力的时空分布，引发了中小尺度对流系统与台风环流的相互作用，形成了新的台风环流构型，引起台风路径的改变（Wu and Wang, 2001; Torn and Davis, 2012）。

热带气旋在对流层的低层和中层为正的位涡异常区（Shapiro and Franklin, 1995），Wu and Wang（2000）用位涡倾向的概念来诊断热带气旋的移动，认为台风会向着一波位涡倾向的最大方位移动，而一波位涡倾向主要受到一波位涡平流和一波非绝热加热分量的影响。Chan et al.（2002）同样用位涡倾向理论得出，当台风移动路径较平稳时，其主要受位涡平流控制，当台风出现不规则路径时，非绝热加热的贡献就较为显著。以上研究都从理想的数值实验研究台风的移动，而缺乏实际台风个例的研究，因此本文选取2011年第9号热带气旋Muifa两次路径转折为例，利用ECMWF和卫星资料以及位涡倾向理论，探讨造成两次路径转折的原因，进一步认识影响台风移动的物理机制。

2 位涡倾向

p坐标下的位涡方程的表达式为

$ P = - g\left[ {(\zeta + f)\frac{{\partial \theta }}{{\partial p}} + \frac{{\partial u}}{{\partial p}}\frac{{\partial \theta }}{{\partial y}} - \frac{{\partial v}}{{\partial p}}\frac{{\partial \theta }}{{\partial x}}} \right], $

(1)

其中，P、g、ζ、f分别为位涡、重力加速度、位温、相对涡度、地转参数，x、y、p分别为纬向、经向和垂直坐标，u、v分别为纬向和经向风速，对上式求时间的全导数得

$ \begin{array}{l} \frac{{{\rm{d}}P}}{{{\rm{d}}t}} = - g\left[ {\frac{{\partial \theta }}{{\partial p}}\frac{{{\rm{d}}(\zeta + f)}}{{{\rm{d}}t}} + (\zeta + f)\frac{{\rm{d}}}{{{\rm{d}}t}}\left({\frac{{\partial \theta }}{{\partial p}}} \right) + } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\frac{{\rm{d}}}{{{\rm{d}}t}}\left({\frac{{\partial u}}{{\partial p}}\frac{{\partial \theta }}{{\partial y}} - \frac{{\partial v}}{{\partial p}}\frac{{\partial \theta }}{{\partial x}}} \right)} \right]. \end{array} $

(2)

将涡度方程：

$ \begin{array}{l} \frac{{{\rm{d}}(\zeta + f)}}{{{\rm{d}}t}} = - (\zeta + f)\left({\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}} \right) + \\ \;\;\;\;\;\;\;\;\left({\frac{{\partial \omega }}{{\partial y}}\frac{{\partial u}}{{\partial p}} - \frac{{\partial \omega }}{{\partial x}}\frac{{\partial v}}{{\partial p}}} \right) + \frac{{\partial {F_y}}}{{\partial x}} - \frac{{\partial {F_x}}}{{\partial y}}, \end{array} $

(3)

代入公式（2），可得

$ \begin{array}{l} \frac{{{\rm{d}}P}}{{{\rm{d}}t}} = - g\left[ {(\zeta + f)\frac{\partial }{{\partial p}}(\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}}) + \frac{{\partial u}}{{\partial p}}\frac{\partial }{{\partial y}}(\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}}) - \frac{{\partial v}}{{\partial p}}\frac{\partial }{{\partial x}}(\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}})} \right] - \\ \;\;\;\;\;g\left[ {(\frac{{\partial {F_y}}}{{\partial x}} - \frac{{\partial {F_x}}}{{\partial y}})\frac{{\partial \theta }}{{\partial p}} + \frac{{\partial {F_x}}}{{\partial p}}\frac{{\partial \theta }}{{\partial y}} - \frac{{\partial {F_y}}}{{\partial p}}\frac{{\partial \theta }}{{\partial x}}} \right], \end{array} $

(4)

其中，F_x、F_y分别为纬向和经向摩擦力，位涡倾向方程为

$ \frac{{\partial P}}{{\partial t}} = {F_1} + {F_2} + {F_3} + {F_4}. $

(5)

公式（5）方程右端的各项分别为

水平平流项（F₁）：

$ {F_1} = - u\frac{{\partial P}}{{\partial x}} - v\frac{{\partial P}}{{\partial y}}. $

(6)

垂直平流项（F₂）：

$ {F_2} = - \omega \frac{{\partial P}}{{\partial p}}, $

(7)

其中，ω为垂直速度。

非绝热加热项（F₃）：

$ {F_3} = - g\left[ {(\zeta + f)\frac{\partial }{{\partial p}}\left({\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}}} \right) + \frac{{\partial u}}{{\partial p}}\frac{\partial }{{\partial y}}\left({\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}}} \right) - \frac{{\partial v}}{{\partial p}}\frac{\partial }{{\partial x}}\left({\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}}} \right)} \right]. $

(8)

摩擦项（F₄）：

$ {F_4} = - g\left[ {\left({\frac{{\partial {F_y}}}{{\partial x}} - \frac{{\partial {F_x}}}{{\partial y}}} \right)\frac{{\partial \theta }}{{\partial p}} + \frac{{\partial {F_x}}}{{\partial p}}\frac{{\partial \theta }}{{\partial y}} - \frac{{\partial {F_y}}}{{\partial p}}\frac{{\partial \theta }}{{\partial x}}} \right]. $

(9)

由上述公式可知，位涡倾向（Potential Vorticity Tendency，简称PVT）由水平平流项（Horizontal Advection，简称HA）、垂直平流项（Vertical Advection，简称VA）、非绝热加热项（Diabatic Heating，简称DH）和摩擦项共同决定。其中，HA能表征外部大尺度环流造成的位涡输送；DH能表征台风内部对流活动分布对位涡的影响。而VA较小，可忽略不计，台风在海面上运动，摩擦项也可忽略不计。因此，PVT主要受HA和DH的共同控制，影响台风运动的外部大尺度环流因素和内部对流结构分布因素就可以分别用HA和DH量化描述。

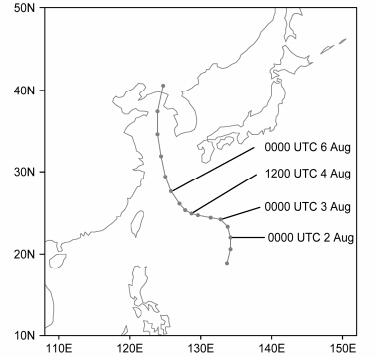
3 Muifa台风外部环流和内部结构分析

热带气旋Muifa于2011年7月28日06:00（协调世界时，下同）在菲律宾以东的洋面上生成后向偏北方向移动，图 1为日本气象厅发布的最佳路径，在8月2日00:00至3日00:00期间，Muifa台风发生第一次路径转折，运动方向由偏北方向快速转为偏西方向，4日12:00之后，开始第二次路径转，运动方向缓慢向北偏转并一直持续到6日00:00之后，此后一路加速北上，并于8月8日18:00在朝鲜西北部沿海登陆。

3.1 环流特征

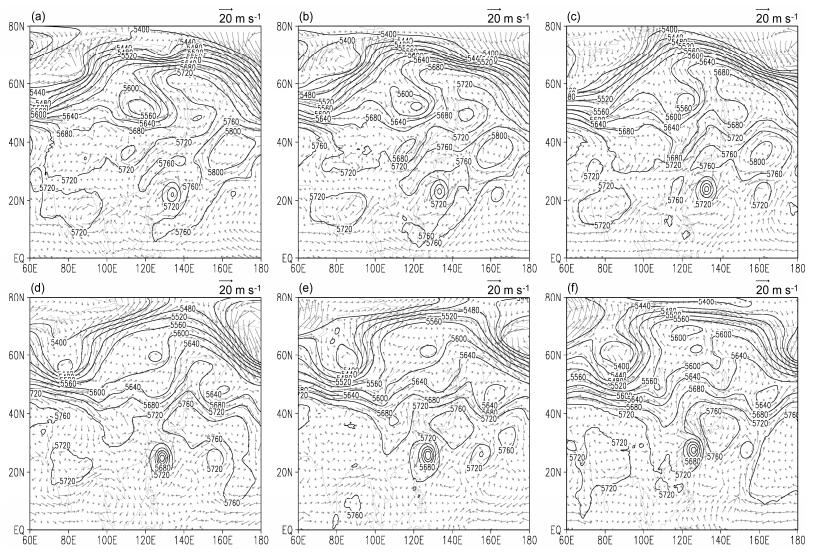
Muifa台风路径转折期间，500 hPa中高纬度对流层中层的大气环流呈两脊一槽的纬向形分布，且槽和脊的位置相对固定，Muifa的两次路径转向就是在上述相对稳定的环流背景下展开。第一次路径转折之前（2日00:00，图 2a），Muifa向偏北方向移动，西太平洋副热带高压的脊线呈西南—东北向，并西伸到Muifa南侧，其北侧有两个断裂的小高压体不断发展增强。2日12:00（图 2b），Muifa北侧两个断裂的小高压体发展强大并与大洋中部的副热带高压连通，使其向北运动受到阻挡，Muifa在三面都被高压体包围的形式下向西偏转。在3日00:00（图 2c），副热带高压脊线由西南—东北向演变成东—西向，此时Muifa完成了第一次路径转折并在副热带高压南侧偏东气流的引导下向西移动。在此期间，Muifa东侧160°E附近的“苗柏”台风正在生成发展并向西移动。

第二次转向之前（4日12:00，图 2d），副热带高压的强度有所减弱，“苗柏”台风开始向北转向并穿越副热带高压，双台风之间的副热带高压有向南发展的趋势，中国大陆上空有中高纬度分裂南下的低压槽，逐渐加强并向Muifa靠近，此后Muifa开始逐渐向北转折。5日06:00（图 2e），“苗柏”台风继续向北穿过副热带高压并使其断裂，双台风之间的高压体进一步向南延伸发展。Muifa西侧的低压槽进一步加深并向其靠近，阻挡了其向西运动并使其向北转向。6日00:00（图 2f），双台风之间的副热带高压进步一向南发展，副热带高压脊线呈南北方向，东移的低压槽已经并入台风环流。此时，Muifa基本完成由西向北的第二次路径转向，在副热带高压西侧偏南气流的引导下加速向北运动。

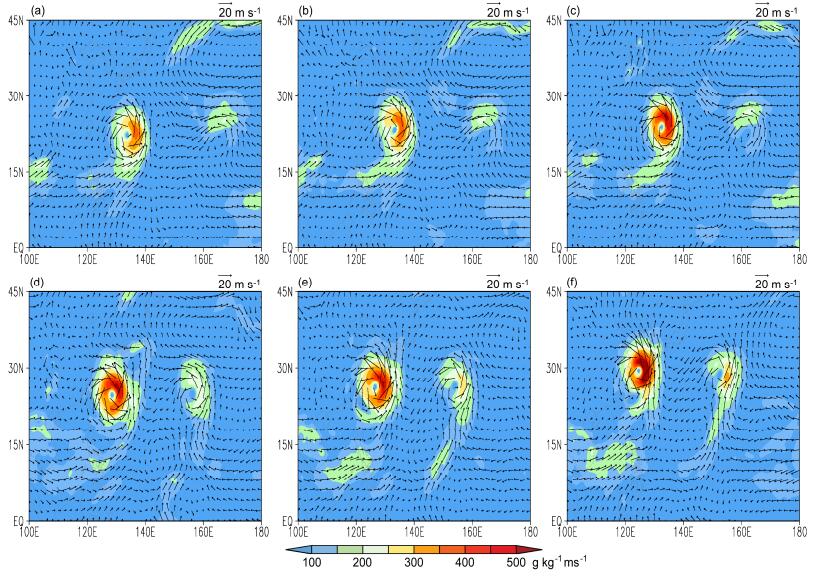
图 3为Muifa台风路径转折期间850 hPa的风场和水汽通量场的演变。第一次路径转折之前（8月2日00:00，图 3a），来自南海的偏西气流和越赤道气流为Muifa提供水汽，160°E附近的“苗柏”台风刚刚生成，出现了明显的气旋性环流。Muifa向西转折过程中（2日12:00，图 3b），越赤道气流明显减弱，南海偏西气流继续维持。3日00:00（图 3c），南海上空的偏西气流对Muifa的水汽输送明显大于越赤道气流，其东侧的水汽通量最大值在450 g kg⁻¹ m s⁻¹以上，Muifa完成第一次路径转折。由此可推测，越赤道气流明显减弱，使得台风环流南风分量减弱可能是导致其向西转折的因素。4日12:00（图 3d），南海上空的偏西气流最为强盛，越赤道气流对Muifa的水汽输送最弱，转而向“苗柏”台风提供水汽，Muifa开始了第二次路径转折。5日12:00（图 3e），南海偏西气流和越赤道气流汇合后从南侧进入Muifa，使其南风分量增强，此时台风正在向北转向。6日00:00（图 3f），由于Muifa进一步向高纬度移动，南海和越赤道的水汽完全以南风的形式为其提供水汽，水汽通量的非对称结构异常明显，其东侧的水汽通量最大值在500 g kg⁻¹ m s⁻¹以上，Muifa完成第二次路径转折，向北加速移动。由此可推测，越赤道气流增强是导致其向北转折的因素。

3.2 引导气流

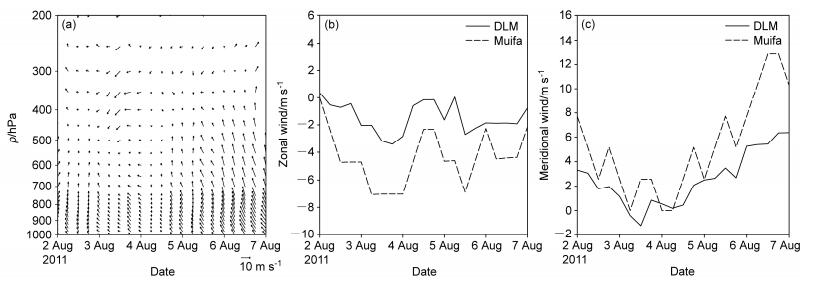
为了定量描述外部大尺度环流对Muifa转向的影响，计算了各层平均引导气流的时间演变（用台风中心5个纬距范围的各层平均风矢量代表平均引导气流）。从图 4a可以看出第一次转向期间，700 hPa以上的平均引导气流的南风分量明显减弱，对流层中下层平均引导气流出现了偏东风分量，导致Muifa停止向北运动并向西转折。4日12:00之后，对流层中下层的平均引导气流的偏东和偏南分量有显著增强，Muifa开始了由西向北的第二次路径转向。Dong and Neumann（1983）从观测分析出，深层平均引导气流（Deep-Layer Mean，简称DLM）（850~200 hPa）比任何单层的引导气流更能指示台风运动，因此计算了深层平均引导气流与台风移动速度随时间的变化（图 4b、c）。

第一次路径转折期间，深层平均引导气流的东风分量和台风移速的向西分量都不断增加，而深层平均引导气流的南风分量和台风移速的向北分量都不断减小，说明Muifa完成了由向北到向西的路径转折。比较发现深层平均引导气流速度要比台风移动速度偏慢，且台风移动速度的变化比深层平均引导气流的变化更加显著，但两者的变化趋势一致。第二次路径转折期间，深层平均引导气流速度仍然比台风移动速度偏慢。两者的纬向分量存在明显波动，但两者变化趋势基本一致。从经向分量来看，深层平均引导气流的经向分量除了在5日12:00至18:00出现减小的趋势之外，其他转向时段都为逐渐增加的趋势，而台风移速的经向分量有显著波动，且在波动中逐渐增加。和第一次路径转折相比，第二次路径转折过程中深层平均引导气流和台风移动速度的波动特征明显，两者的对应关系不如第一次转折期间显著。

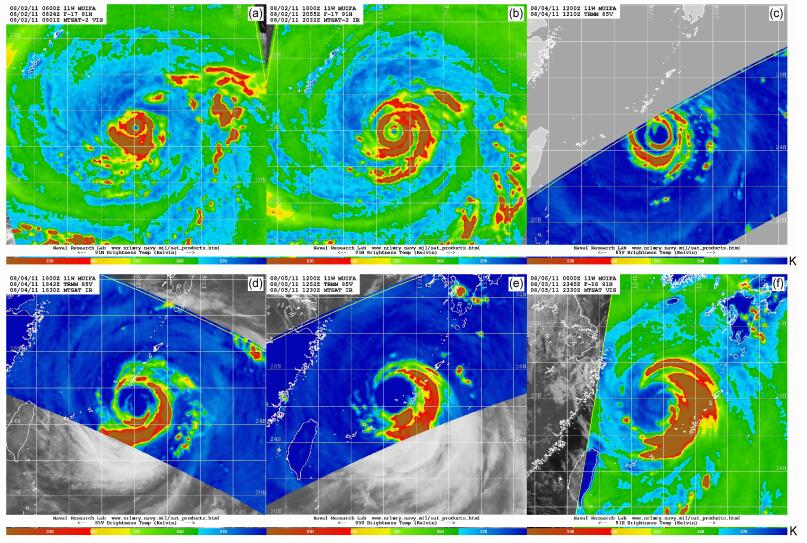
3.3 内部结构特征

上述外部因素过程固然是影响台风运动的因素，但台风路径受到外部和内部过程的共同作用，台风内部的结构变化，特别是眼墙对流的分布状况在台风移动中起着重要的作用，因此以下对Muifa内部的对流特征进行了分析。图 5为MTSAT卫星红外云图和TMI（TRMM Microwave Imager）/SSMI（Special Sensor Microwave Imager）微波探测器85 GHz频道红外亮温叠加图，该通道增强了较暖粒子的信息，能有效探测水汽、云水和雨水物质的分布。图 5a和b为Muifa台风第一次路径转向过程中眼墙和螺旋云带的分布，2日08:24（图 5a），台风眼区收缩得很小，螺旋云带主要集中在眼墙的南侧。2日20:55（图 5b），台风眼区扩大，眼内区南侧的对流螺旋云系合并到眼墙之中，同时眼区东侧出现了较强的螺旋云带。由于卫星观测资料的限制，无法捕捉到第一次路径快速转折期间内部对流结构变化的完整过程，但从这两个时刻可推测第一次路径转折期间，眼墙的对流一直维持较为对称的分布状态。

图 5c–f为第二次路径转折过程中眼墙和螺旋云带的演变。在转向前的4日12:00左右（图 5c），Muifa台风出现了对称的双眼墙结构，此后开始了由西向北的第二次路径转折。4日18:00，原来较为对称的双眼墙结构逐渐消失，在眼区南侧出现了较强的螺旋云带，螺旋云带并入台风眼墙使得南侧眼墙对流强盛，造成了眼墙对流结构出现明显的非对称分布（图 5d）。Muifa台风的这种螺旋云带及眼墙的非对称结构一直贯穿整个第二次转折过程，但眼墙对流的分布在后期发生变化，对流活动逐渐由南侧眼墙转移到东侧眼墙（图 5e、f）。

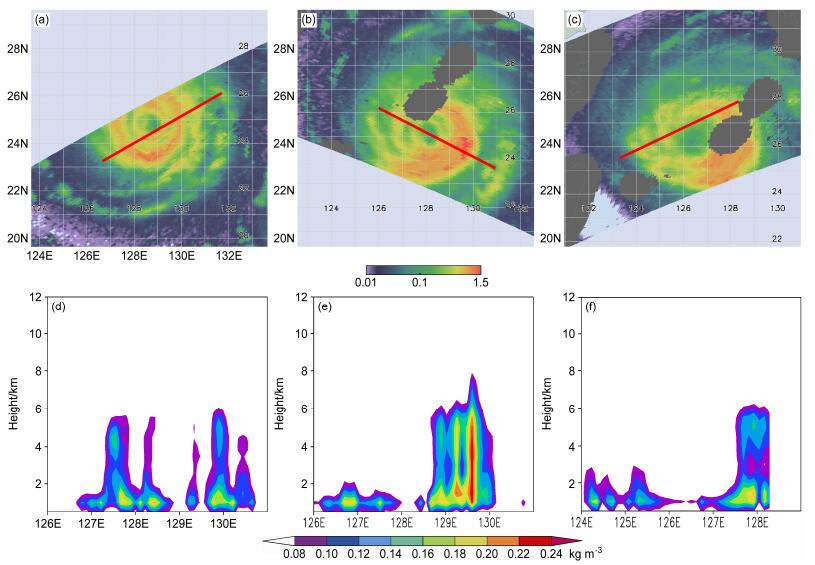
为了细致地反应“梅花”内部细致的微物理结构，图 6给出了TRMM卫星探测的云水物质的垂直积分以及沿着红线剖面的垂直分布，由于卫星资料时间分辨率的限制，仅探测到第二次路径转折前和转折中的三个时刻。第二次路径转折前，云水含量垂直积分的分布显示出之前描述的对称双眼墙结构（图 6a），沿着卫星轨道（红线）的垂直剖面同样看出双眼墙结构以及东南侧的螺旋云带，其中外眼墙较厚较强，内眼墙较薄较弱（图 6d）。转折过程中（图 6b），双眼墙结构仍然维持，其中内眼墙有所减弱，螺旋云带从南侧和东侧合并进入外眼墙，使得外眼墙明显增厚增强并形成非对称结构。垂直剖面清楚地显示，西北侧内外眼墙明显减弱，高度降低，而东南侧的外眼墙与螺旋云带合并后强度显著增强（图 6e）。5日12:53，双眼墙的结构已经破坏，西侧的内外眼墙基本消失，而东南侧的螺旋云带和眼墙合并使得眼墙的非对称结构继续维持（图 6c）。垂直剖面图看出东侧眼墙发展高度的有所降低，云水含量较上一时次减小（图 6f），这时台风强度开始减弱。

综上所述，在Muifa台风第二次路径转向期间，眼墙对流结构经历了对称到非对称的转变，眼墙结构的变化必然会导致台风环流的改变从而影响台风的运动，这在路径转折过程扮演了多大的作用？非对称的对流结构对台风转向会产生何种影响？下文将进行探讨。

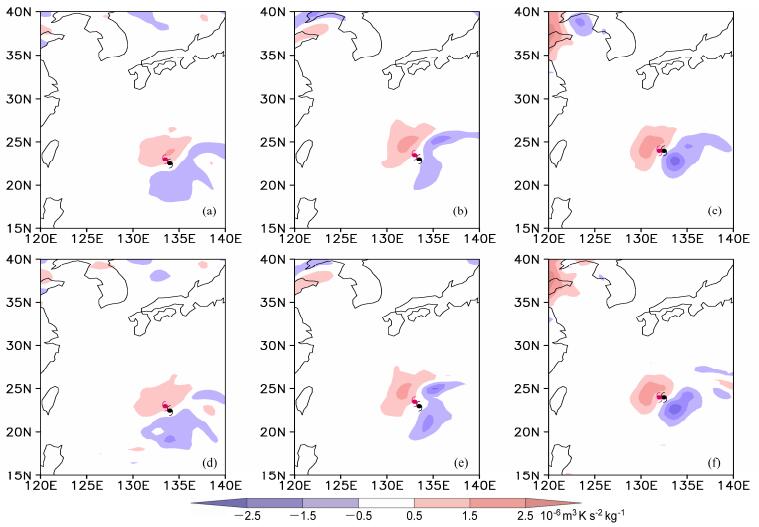
4 位涡倾向在Muifa路径转折过程的诊断

利用位涡倾向方程计算了Muifa台风两次路径转折过程中HA、DH和PVT从950~200 hPa垂直积分的演变。在第一次路径转折期间，DH比HA小一个量级，对PVT的贡献很小，因此在图 5中省略了DH的演变。2日00:00，第一次路径转向开始时，HA和PVT的正值区都位于台风中心的西北侧，负值区位于台风中心西南侧，即表现出西北—东南分布（图 7a、图 7d），由下一时刻台风中心位置（红点）可知，台风正朝着西北侧的正值区移动。2日12:00，第一次路径转向过程中，HA和PVT的分布仍然呈现西北—东南分布状态，由下一时刻台风中心位置可看出，台风正朝着HA和PVT的最大正值中心移动（图 7b和图 7e）。3日00:00，第一次路径转向后，HA和PVT的分布由路径转向时的西北—东南分布演变成了东负西正的分布，之后台风向着西侧的HA和PVT正值中心运动（图 7c和图 7f）。从以上分析可得出，PVT的正值区能较好地指示Muifa台风第一次路径转折过程，HA所表征外部环流因素是造成第一次路径转折的主要原因。

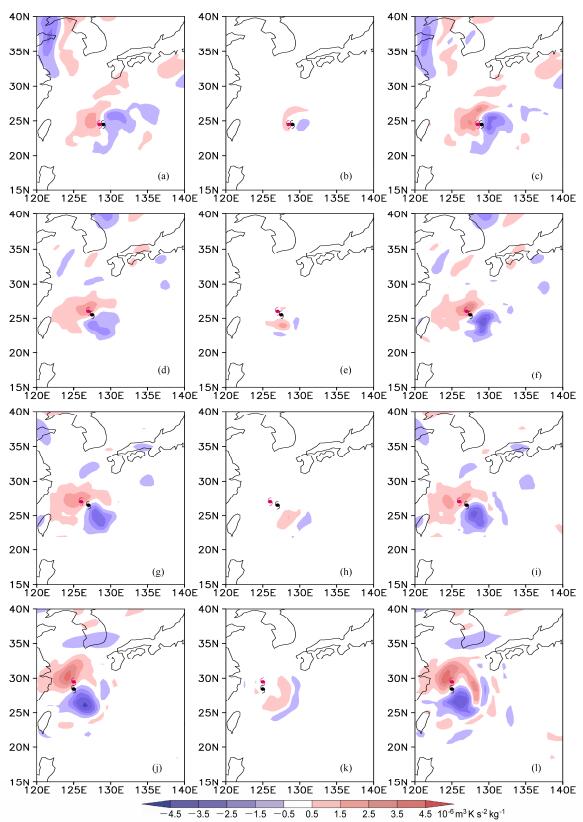
图 8为Muifa台风第二次路径转折过程期间HA、DH和PVT垂直积分的演变。第二次路径转向之前的4日06:00，HA、DH和PVT都为东负西正的分布形式（图 8a、b、c），其中DH的强度较弱，PVT的分布主要受HA控制，此时台风向着正西方向的PVT最大正值区运动。5日00:00，第二次路径转向过程中，HA和PVT的分布由转向前的东西分布演变成了西北—东南分布（图 8d、f），HA和PVT的正值区位于台风中心西北侧，负值区位于台风中心东南侧，台风向着西北侧的最大正值区移动。从以上对Muifa的内部结构特征分析可知，此时眼墙对流结构出现明显的非对称分布，对流集中在南侧眼墙（图 5d），DH的分布也证实了这一特征，从图 8e可看出，DH的分布也出现了明显的非对称分布，在台风中心南侧出现了正的DH区，这与台风中心南侧正的HA和PVT分布形式相反，因此，DH对台风向西北转向起到抑制作用，从Muifa的经向移动速度演变（图 4c）看出，此时台风向北移速约为2.6 m s⁻¹。5日12:00，HA和PVT继续维持西北—东南分布，台风继续向着西北侧HA和PVT的正值区转向（图 8g、i）；DH继续维持非对称分布，正的DH区从台风中心南侧转移到东南侧，强度有所减弱，从以上对内部结构特征分析可知，此时眼墙对流活动也集中到了东南侧眼墙（图 5e）。与上一时刻类似：台风中心东南侧正的DH的分布与HA和PVT为负的分布相反，DH对台风向北转向的抑制作用继续维持，台风向北移速约为7.7 m s⁻¹（图 4c）。6日06:00，Muifa完成了第二次路径转折并向北运动，此时HA和PVT分布从转向期间的西北—东南演变成了南北向（图 5j、l）；从台风的内部结构特征（图 5f）以及DH正值区的分布（图 8k）可知，对流活动集中到了东侧眼墙，此时DH对台风转向的抑制作用消失，台风向北快速移动，移速为10.3 m s⁻¹（图 4c）。从以上分析可得出，PVT的正值区能较好地指示Muifa台风第二次路径转折过程，HA所表征外部环流因素仍然是此次路径转折的主要原因，DH对路径转折有抑制作用。

5 结论和探讨

（1）分析Muifa台风两次路径转折过程的外部大尺度环流，发现第一次路径转折主要受副热带高压脊线调整的影响；而中高纬西风槽的接近，副热带高压南落是造成第二次路径转折的因素。引导气流的分析结果表明：第一次路径转折过程中，深层平均引导气流速度和台风移动速度的变化趋势一致；第二次路径转折过程中两者的波动特征明显，两者的对应关系不如第一次转折期间显著。

（2）卫星资料揭示了Muifa台风两次路径转折过程的内部对流结构，发现第一次路径转折过程中眼墙对流结构一直维持较均匀的对称结构；第二次路径转折过程中，台风眼墙出现了明显的非对称结构，眼墙对流活动由南侧眼墙转移到东侧眼墙。

（3）位涡倾向方程揭示出两次路径转折的机制：第一次路径转折期间，DH对PVT的影响很小，PVT主要受到HA控制，PVT能较好地指示台风的转向和移动，因此，外部环流因素是第一次路径转折的主要原因。第二次路径转折过程中，PVT受到HA和DH的共同控制，其中HA对PVT的影响较大，主要控制台风的移向，台风向着HA和PVT的正值区运动，DH对台风转向有抑制作用，因此，第二次路径转折受到外部环流和内部结构的共同影响。

（4）本文的研究发现在第二次路径转折过程中伴随着眼墙对流结构的非对称变化，但究竟是台风路径转折造成眼墙对流的非对称结构，还是眼墙对流的非对称结构引起台风的路径转折？因此，下一步研究将展开高分辨的数值模拟，在模拟出Muifa台风两次路径转折的基础上，对引导气流与台风环流的相互作用以及眼区的动力与微物理过程的相互作用等台风内外部过程展开深入的研究。