气候变化、大气污染和大气质量是当今世界十分关注的问题,而在这两者之中,大气中气溶胶的种类和含量都是很重要但又未清楚认识的一些因素。气溶胶大致可分为人为排放和自然排放两类,后者以沙尘和海盐粒子为主,它们都是在风力的驱动下由地球表面刮起进入大气边界层最低层,这就是所谓发射过程,相应地有地表发射通量,或称生成函数(即Sea-Spray Generation Function,简称SSGF)。在大气边界层内,这些粒子受重力以及各种尺度气流的动力和物理过程作用,甚至粒子间的相互作用,使得粒子或悬浮,或沉降重回地面,或上扬至边界层上层再上至对流层,可总称为垂直传输过程。发射和传输这两项过程都十分复杂,而且沙尘多起于沙漠及其周边,海盐粒子源于海洋,观测困难,资料奇缺。因此无论对局地的还是全球平均的气溶胶表面垂直通量以及气溶胶在大气柱中的含量,不同作者给出的数值均有很大的不确定度,甚至可在数量级上有差别,尤其是海洋气溶胶(Andreas, 1998, 2002, 2010;Fairall et al., 2009;Jaeglé et al., 2010;Veron et al., 2012)。
就海盐气溶胶来说,在较平静的海面上,它是海表和浪间的气泡破裂形成小水滴的弹射所产生,这种情况下的发射通量(或生成函数)今大体已比较确定。但在大风浪情况下发出的较大水滴和飞沫(水滴半径r0>20 μm)则是大风撕裂浪冠水体而抛射到大气所致。由于直接观测不多,有关的生成函数SSGF有很大的不确定度,甚至可相差一到数个数量级。关于这方面,已有许多文献加以讨论(Andreas, 1998, 2002, 2010;Petelski et al., 2005;Zhao et al., 2006;Fairall et al., 2009;Mueller and Veron, 2009a;Andreas et al., 2010;Jaeglé et al., 2010;Veron et al., 2012;赵栋梁,2012)。
至于海盐气溶胶自海面和浪尖发射出来之后,是怎样变成垂直传输通量,以及进一步在大气边界层中停留和穿透大气边界层而进入对流层,成为大气中的气溶胶,这过程也非常复杂。水滴的发射速度只是其初始速度,此后在重力和水滴相对于流体运动所致的多种力作用下运动,甚至水滴还有蒸发和相互碰撞等。在这些因素综合作用下,就决定了含盐水滴粒子是上升、悬浮、还是下沉回到海面。这些都极其依赖于当地的大气边界层的结构和特性。至今,一方面缺乏在海上大气中海盐气溶胶通量和浓度的足够资料,二来也缺乏海上大风情况下大气边界层特性观测的足够资料,从而有不少重要的特性尚未被揭露。在第一个问题上,就作者所知,目前最好的资料是NOAA发布的Pacific Marine Environmental Laboratory(PMEL)1993~2008年的6条航线的船上观测资料,美国迈阿密大学和全球自动观测网AErosol RObotic NETwork(AERONET)共计15个站点的观测资料(Jaeglé et al., 2010),由此来确定出气候平均情况,由于观测重点是成为海盐气溶胶粒子的浓度,半径大于10 μm的大粒子都被人为删除了。至于海上大风边界层特性的观测资料则只有个例(Black et al., 2007;Zhang et al., 2008),但可惜也未注意到大风情况下边界层风场脉动的特点。以致直到目前,研究者们都只用到湍流传输理论将海盐气溶胶粒子的生成函数与扩散和沉降联系起来(Andreas, 1998, 2010;Fairall et al., 2009;Mueller and Veron, 2009b;Andreas et al., 2010),而没有直接研究大风期间粒子在整个大气边界层中的传输过程。在现有文献中,都认为大水滴(形成时的初始半径r0≥20 μm)从浪冠射出后直接或很快地下掉回海面,不可能飞出边界层低层。最鲜明的叙述可见Andreas(2010),尤其是其文中的图 1和图 7。但事实上,尽管观测资料很少,在大气边界层中也常观测到有大水滴存在,甚至其r0>100 μm乃至1 mm。这说明,必定是除湍流扩散混合过程外,还有别的过程存在,使得大水滴能够飞升,此问题值得研究。须知,水滴含盐量正比于其r03,故从海洋向大气输出的盐通量来说,一个r0=100 μm的大水滴抵得上106个r0=1 μm的小水滴。
|
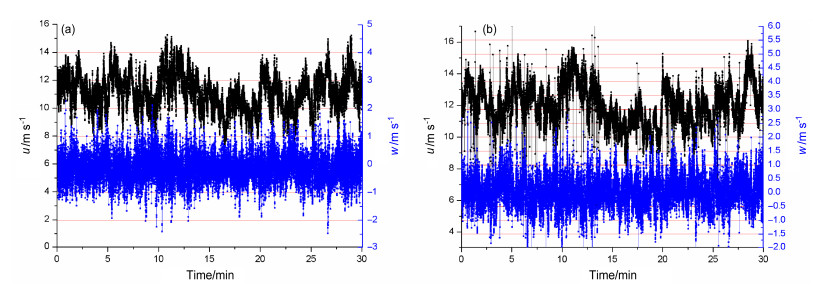
图 1 2012年3月23日21:00~21:30(北京时,下同)博贺海上观测平台(a)8 m和(b)27 m观测高度冷涌期的风场时间曲线 Figure 1 Wind speed time series during the cold surge period of 2100 BT–21:30 BT (Beijing time) 23 March 2012 at Bohe marine observation platform at (a) 8 m and (b) 27 m high levels |
|
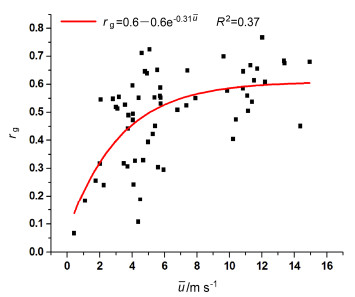
图 7 大风期阵风扰动的相干性指数 |
本文就只研究讨论大水滴在大气边界层的运动和传输问题。第2节叙述海上大风期大气边界层的特性。使用我们近年来在海上直接观测的资料,发现大风期阵风扰动(广义来说,就是频率在1/60~1/600 Hz的脉动)非常强,且相干性也很强,它迭加于平均流和高频湍流脉动(频率大于1/60 Hz)之上。在风速小时阵风扰动则不常有,具偶发性,强度也弱。此外,还用平均水平风速作参量来表达,给出一些关于对阵风扰动和湍流脉动的特性的参数化公式,以利于计算应用。第3节叙述大水滴在大气边界层中的运动轨迹的计算方法。第4节给出数值模拟结果,用的是重粒子在具有拉格朗日随机过程的流体中运动的Thomson模式,气流场则是由观测得到的平均气流场和脉动场(包括用实测得到的和第2节给出的参数化公式计算结果),结果是大风期的阵风甚至还有平均气流的上升分量可使大水滴能飞出大气边界层低层。第5节给出由此算得的水滴上扬进入大气边界层低层的比率,及其参数化公式。第6节和第7节为小结和进一步的讨论。
2 大风期海上大气边界层的特性2008年起,我国在广东省沿海建立了一些海洋气象站,例如茂名市博贺站(北纬21°27′37″,东经111°19′24″),包括岸边上的北山站、海上观测塔平台[离岸边6 km,台下水深11 m,塔上有四层超声仪观测(Gill R3-50型,采样频率20 Hz,分辨率0.01 m s−1,测量精度<±1%RMS,Root Mean Square),从离海面8 m起至35 m]和离岛(峙仔岛)高塔观测。峙仔岛很小,高出水面10 m,周围水深6~10 m,其上的塔高100m,有多层风杯(NRG-Symphonic型,启动风速0.78 m s−1,测量范围0~70 m s−1)和一层超声观测(Gill-Windmaster Pro.型,采样频率10Hz,测量范围0~45 m s−1,测量精度<±1%RMS)。三站间的距离在10 km以内。依据这些观测站,取得了几年冬、春季冷涌大风和几次台风过程的观测资料,尤其是强台风Hagupit(2008年9月24日)过境全过程的大气边界层中每10 min平均风场和脉动场(采样频率为10 Hz)的资料。这些资料的选例分析结果见Cheng et al.(2014, 2015)。
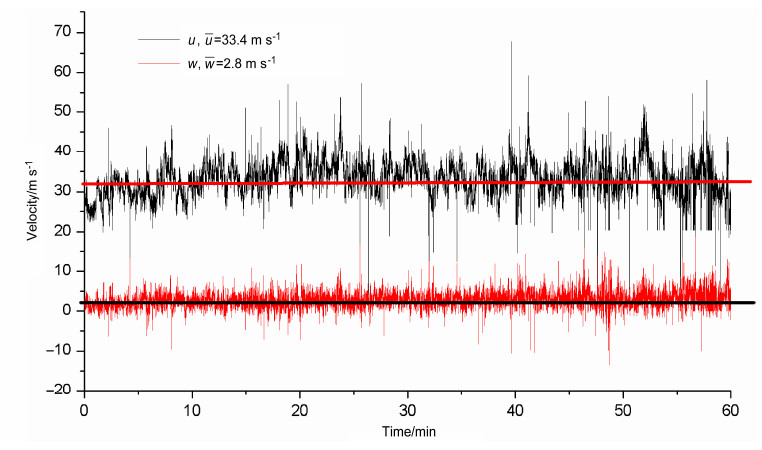
图 1和图 2给出冷涌期半小时和台风期一小时超声仪测得的原始记录。可以很明显地看出,大风期含有很强的脉动。而脉动(按通常记为u′、v′、w′),又可明显分为两类,其性质差别很大。一类是几乎是随机的,尤其是高频段频率大于1/60 Hz(即周期小于1 min);另一类是较有明显结构、有较明显规律的及具有较强相干性的扰动,频率在1/60~1/600 Hz之间(周期在1~10 min.之间)。前者大体上属于Kolmogorov的惯性湍流区,可以较好地应用已有的湍流理论。而后者已远离惯性区,不满足经典湍流理论的条件。故将两部分区分开来分别分析。为简单计,我们对脉动场作Fourier分解,取频率大于1/60 Hz的为前者,记作(ut, vt, wt),并简称为湍流脉动;而频率在1/60~1/600 Hz之间的为后者,记作(ug, vg, wg),并称之为阵风扰动。按通常方法,我们将风场分为10 min滑动平均的风场(u,v, w),和脉动场(u′、v′、w′),于是有u'=ug+ut,再取u沿顺风方向,于是v=0。
|
图 2 2008年9月24日04:00~05:00峙仔岛离海面70 m高层观测台风期的风场时间曲线 Figure 2 Wind speed time series during the typhoon period of 0400 BT–0500 BT 24 September 2008 at 70 m height above the Zhizi Island |
下面给出本文需要进一步用到的一些结果:
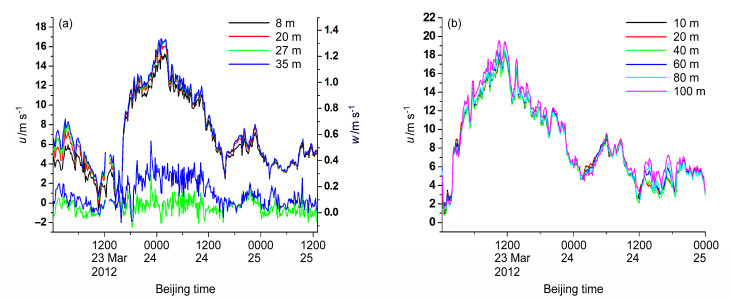
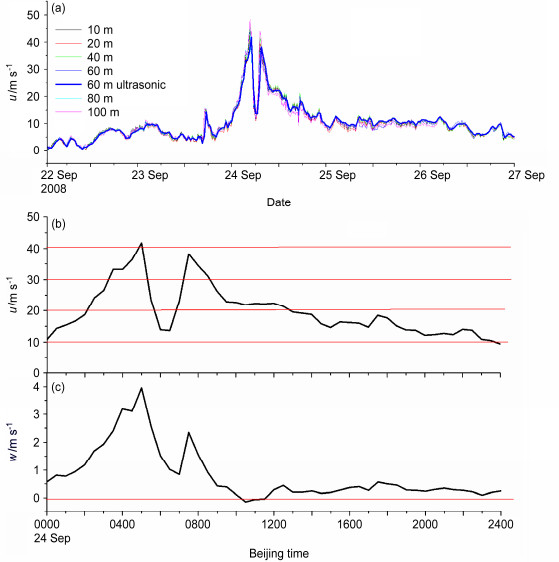
(1)在大风期,10 min平均的水平风速u,基本上不随高度而变,而且伴有上升气流,即w>0。在冷空气入侵的冷涌时期是如此,如图 3;在台风期也是如此,且上升气流w很强,甚至有w>1 m s−1,如图 4(由于w在靠近平台基的两层明显受台基的影响,图 3中未给出)。
|
图 3 2012年3月23~25日(a)海上平台、(b)峙仔岛塔观测站冷涌大风期各高度层观测的 |
|
图 4 2008年台风Hagupit过境时峙仔岛观测塔9月22~27日观测的(a)各高度层的以及9月24日70 m高度层的(b) |
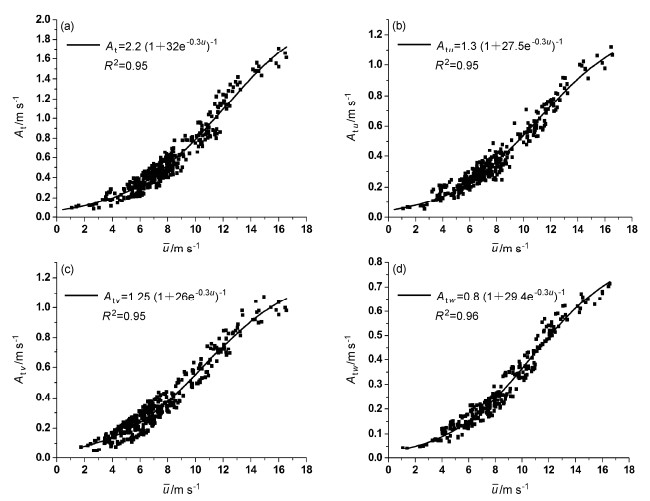
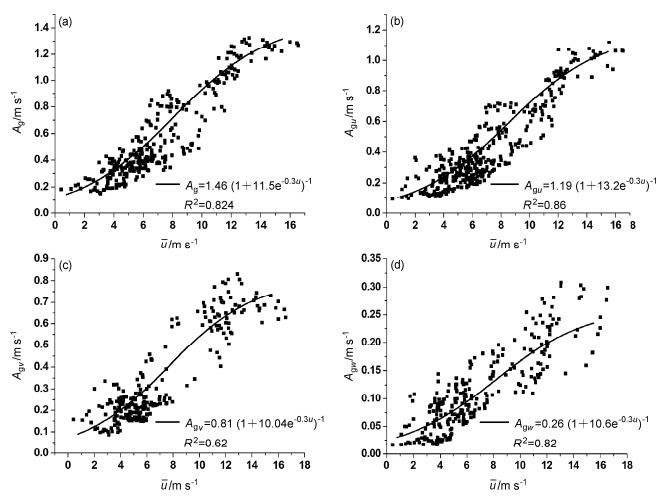
(2)在大风情况下,具有很强的湍流脉动和阵风扰动,其振幅At和Ag的三分量(Atu, Atv, Atw)和(Agu, Agv, Agw)都很大。它们都可以较好地用参数化公式表达,主导参数为平均水平风速u(因在边界层低层u大体不随高度变化,u也理解为常用的海面上10 m高处的风速U10)。图 5是At和Atu、Atv、Atw随u的变化,图 6是Ag和Agu、Agv、Agw随u的变化,拟合的回归方程(参数化公式)亦给于图 5中(Cheng et al., 2015)。
|
图 5 大风期的(a)湍流脉动振幅At和其分量(b)Atu、(c)Atv、(d)Atw与u的关系 Figure 5 (a) The amplitude of turbulent fluctuation and (b–d) its three components against u |
|
图 6 大风期的(a)阵风扰动振幅Ag和其分量(b)Agu、(c)Agv、(d)Agw与u的关系 Figure 6 (a) The amplitude of gusty wind fluctuation and (b–d) its three components against u |
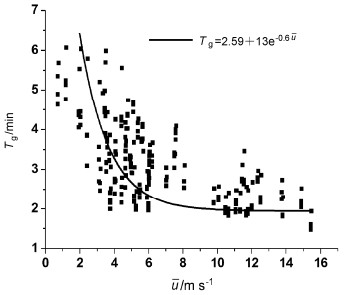
(3)阵风扰动具有较强的相干性指数|rg|(Zeng et al., 2010),即阵风扰动的水平分量和垂直分量负相关,其相关系数rg的绝对值常大于0.5。|rg|和阵风等效周期Tg [即以能谱为权重定义的周期,见Zeng et al.(2010)]及其由u表示的参数化公式见图 7和图 8。
|
图 8 大风期阵风扰动的等效周期Tg与水平风速的相关 Figure 8 Change in gusty wind equivalent period Tg with horizontal velocity during high wind episodes |
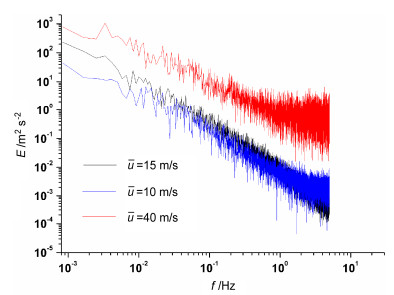
(4)大风情况下,风速脉动的动能能谱如图 9,可见频率高于1/60 Hz的能谱大体上仍满足-5/3幂律,即属于惯性湍流区(Kolmogorov inertial subrange),可以用其理论;而频率在1/60~1/600 Hz的阵风扰动的能谱分布就与惯性湍流区很不相同。由此可见我们将脉动分为这样两部分是合适的。在下面我们讨论气溶胶重粒子传输时可以很清楚地看出它们起很不同的作用,尤其在理论模式的处理方法上就很不相同(由图 9可见,峙仔岛塔上的超声仪在频率大于2 Hz时有误差,不过这不给我们的分析和计算结果造成大的误差)。
|
图 9 大风时脉动动能的能谱分布。黑色曲线为冷涌大风时,蓝色和红色为Hagupit台风时 Figure 9 Power spectra of fluctuation energy during high wind episodes (black line: cold surge; blue and red lines: typhoon Hagupit) |
水滴和沙尘等重粒子,如半径过大,特别是半径r0≥10 μm,它在大气边界层中的传输,不能被看作保守量而简单地用平流加扩散来处理,因为受惯性和重力的作用,重粒子并不跟随原先它所在流体微团一起运动,二者的轨迹会分离。较好的方法是应用拉格朗日随机模式计算粒子在具有湍流的大气中运动的轨迹。例如应用Thomson推广了的Langevin方程(Thomson,1987)作数值模拟。我们曾用这种方法计算沙尘粒子的垂直传输过程,其中大气边界层中的平均场直接用实测的每10 min平均的流场,而脉动也用实测或用由观测作出的参数化公式表示。结果是相干的阵风扰动,作为有足够强度的空间尺度很小的迷你平流将沙尘一阵阵传至边界层上层。但若删去阵风,只靠湍流混合,则沙尘只能聚集在最底层(Zeng et al., 2010;Cheng et al., 2011, 2012)。沙尘暴刚开始时,目测也可以很清晰地看到这样的图像(Cheng et al., 2012)。这里所谓“迷你尺度”是指空间尺度比一般所说的“小尺度”要小,而比一般说的“微尺度”要大。按照泰勒冻结假设,则由观测到时间序列可算得其水平尺度(波长)为500~1500 m,垂直尺度(波长)为50~150 m。在台风情况下,垂直尺度300 m甚至更大。
我们想象,既然海面上大风期存在着较强的相干阵风扰动,而且甚至还有大尺度的上升速度,由破头浪冠发射出来的较大的水滴(如果不是太重的话),应该有相当的数量能够扬上大气边界层,而不是全部降落回海面上。为此,我们做了许多数值模拟。
Kolmogorov(1962)的湍流理论对高雷诺数粘性不可压流的均匀惯性湍流区已被证实是相当正确的。在实际的大气边界层中,总是雷诺数ReL≫1。即使在大风情况下,频率高于1/60 Hz的湍流脉动仍可看作惯性区(见图 9);而“均匀”性一般可代之以“局部均匀性”。对该区(即ut、vt、wt)来说,Kolmogorov理论可以应用。此外,若相邻两时刻的间隔Δt远大于Kolmogorov时间尺度
| $ \left\{ \begin{array}{l} {\rm{d}}z = \left({\bar w + {w_{\rm{g}}} + w} \right){\rm{d}}t, \\ {\rm{d}}w = a\left({z, t} \right)w{\rm{d}}t + b\left({z, w, t} \right){\rm{d}}\xi, \end{array} \right. $ | (1) |
而其水平坐标(x, y)与湍流无关,由下列方程给出:
| $ \left\{ {\begin{array}{*{20}{c}} {{\rm{d}}x = \left({\bar u + {u_{\rm{g}}}} \right){\rm{d}}t, }\\ {{\rm{d}}y = \left({\bar v + {v_{\rm{g}}}} \right){\rm{d}}t, } \end{array}} \right. $ | (2) |
其中,
| $ \left\{ {\begin{array}{*{20}{c}} {a\left({z, t} \right) = -\frac{{{c_0}}}{2}\frac{{\bar \varepsilon }}{{\sigma _w^2}}, }\\ {b\left({z, w, t} \right) = \sqrt {{c_0}\bar \varepsilon }, } \end{array}} \right. $ | (3) |
其中,c0=2.1是Kolmogorov常数;
考虑到大气中的气溶胶粒子主要受粘曳力和重力作用,又因粒子的密度
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{u_{\rm{p}}}(t)}}{{{\rm{d}}t}} = \frac{f}{{{\tau _{\rm{p}}}}}(\bar u(z, t) + {u_{\rm{g}}}(z, t) - {u_{\rm{p}}}(z, t)){\rm{ }}, \\ \frac{{{\rm{d}}{v_{\rm{p}}}(t)}}{{{\rm{d}}t}} = \frac{f}{{{\tau _{\rm{p}}}}}(\bar v(z, t) + {u_{\rm{g}}}(z, t) - {u_{\rm{p}}}(z, t)){\rm{ }}, \\ \frac{{{\rm{d}}{w_{\rm{p}}}(t)}}{{{\rm{d}}t}} = \frac{f}{{{\tau _{\rm{p}}}}}[(\bar w(z, t) + {w_{\rm{g}}}(z, t) + w(z, t)) - {w_{\rm{p}}}(z, t)] - g, \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{x_{\rm{p}}}}}{{{\rm{d}}t}} = {u_{\rm{p}}}, \\ \frac{{{\rm{d}}{y_{\rm{p}}}}}{{{\rm{d}}t}} = {v_{\rm{p}}}, \\ \frac{{{\rm{d}}{z_{\rm{p}}}}}{{{\rm{d}}t}} = {w_{\rm{p}}}, \end{array} \right. $ | (5) |
其中,公式(4)右端第一项是流体对粒子的拖曳力,而g是重力加速度。τp为质点的张弛时间,表示粒子在Stokes拖曳力作用下速度减小为原来的1/e所用的时间:
| $ {\tau _{\rm{p}}} = \frac{{{\rho _{\rm{p}}}d_{\rm{p}}^{\rm{2}}}}{{18\mu }} $ | (6) |
其中,μ为空气粘性系数(μ=ν/ρa)。f为Stokes曳力系数,当Rep≪1时,流动为Stokes流,且f=1;当Rep≥1,有(Clift et al., 1978)
| $ f = 1 + 0.15Re_{\rm{p}}^{0.687} $ | (7) |
公式中,
求解公式(1)和(2),得到空间各点流体的湍流垂直速度w,代入公式(4),同时平均流
为简化计算,特别是我们只有单点的观测时间序列,在下一节的数值模拟中,我们将只考虑(x, z)平面,略去公式(4)和(5)中的关于vp和yp的方程。还要指出,在上面的方程中,是设流体运动不受其中的气溶胶粒子的影响,且粒子间的运动互不影响,这在水滴在破头浪冠之上运动时是可以的。但在破头浪附近,即当水滴发射时或掉落其下时不行(Muell and Verson, 2009b)。
4 数值模拟结果示例用上节的模式作数值模拟,取Δt=min (τp, 0.05TL),它满足上节所述的条件。取二维空间(x, y),z=0为破头浪冠高度,103个水滴,由其中的一段0≤x≤Δx上作Gaussian随机发射,中点
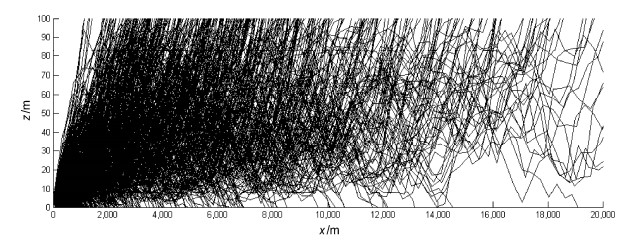
我们分别取第2节中冷涌大风期和飓风时一小时实测的风场
|
图 10 2012年3月23日21:00~22:00冷涌大风时期水滴轨迹的数值模拟结果。rp=70 μm,取为实际资料,u,ug和wg取为实际资料, u≈15m/s;取δ·w(实际δ·w);半小时内飞上100 m高度的水滴数N1=433,下沉至海面的水滴数N2=567,悬浮于0~100 m层的水滴数N3=0 Figure 10 Simulation results of the droplet trajectories, rp=70 μm, u, ug and wg are wind velocities observed during the cold surge period of 2100 BT–2200 BT 23 March 2012, u≈ 15 m/s, δ ·w = 0 (δ ·w > 0 for observed velocity). N1=433, N2=567, N3=0 |
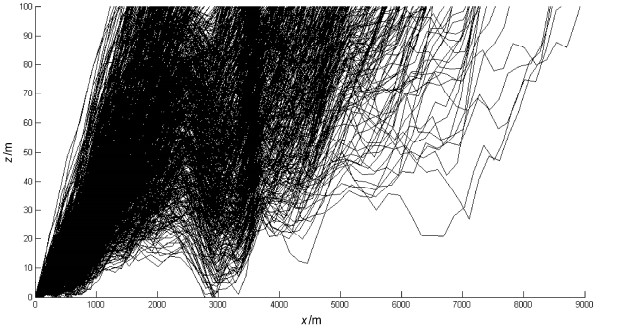
|
图 11 008年9月24日04:00~05:00飓风眼的前壁大风时期水滴轨迹的数值模拟结果。rp=100 μm,u,ug和wg取为实际资料,u ≈ 35 m/s;取δ·w = 0(实际δ ·w > 0);N1=863,N2=137,N3=0 Figure 11 Simulation results of the droplet trajectories, rp=100 μm, u, ug and wg are wind velocities observed during 0400 BT–0500 BT 24 September 2008 at the front quadrant of the typhoon eyewall, u≈ 35 m/s, δ ·w= 0 (δ ·w > 0 for observed velocity). N1=863, N2=137, N3=0 |
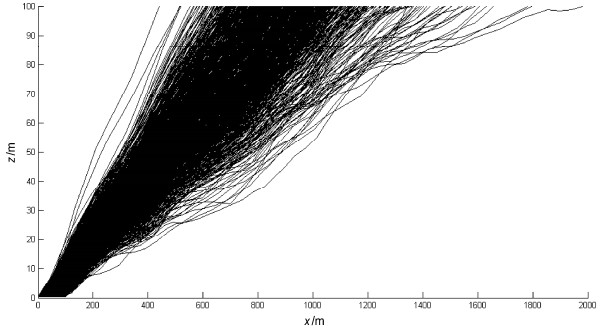
|
图 12 同图 11,但取δ ·w为实测值,δ ·w ≈ 3 m/s;N1=1000,N2=0,N3=0 Figure 12 Same as Fig. 11, except that δ ·w is observed and δ ·w ≈ 3 m/s. N1=1000, N2=0, N3=0 |
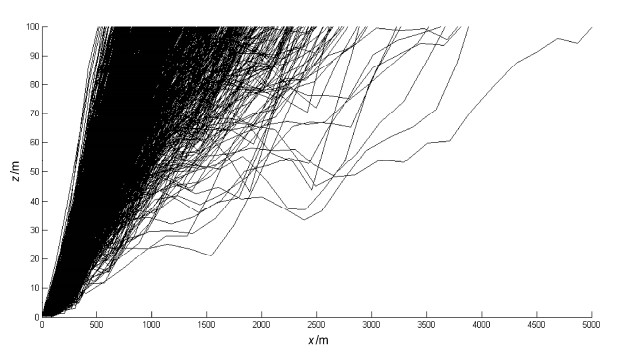
|
图 13 同图 11,但为06:00~07:00处于飓风眼附近,u ≈ 15 m/s,并取δ ·w为实测值,δ ·w ≈ 1 m/s;N1=1000,N2=0,N3=0 Figure 13 Same as Fig. 11, except that u u w, and g g are wind velocities observed during 0600 BT–0700 BT 24 September near the typhoon eye, u ≈ 15 m/s, δ ·w is observed and δ ·w ≈ 1 m/s. N1=1000, N2=0, N3=0 |
由这些图可见,在大风情况下,即使不考虑w>0,在相干阵风扰动的作用下,rp>70 μm的水滴有相当大的比例可飞上100 m高以上的大气中。
考虑到目前所有的天气和气候数值模式都不能正确地模拟出阵风扰动。为了应用起见,我们用参数化公式表示w和阵风扰动(ug,wg)以及湍流特性参数,再作数值模拟,取
| $ {u_{\rm{g}}} = {A_{{\rm{g}}u}}\cos (\frac{{2{\rm{ \mathsf{ π} }}}}{{{T_{\rm{g}}}}}t), {w_{\rm{g}}} = {A_{{\rm{g}}w}}\sin (\frac{{2{\rm{ \mathsf{ π} }}}}{{{T_{\rm{g}}}}}t + {\alpha _{\rm{g}}}), $ | (8) |
其中,Agu、Agw、Tg由u表达的参数化公式,已在第2节中给出;而且
| $ {\alpha _{\rm{g}}} = {\sin ^{ - 1}}{r_{\rm{g}}} = \frac{{{r_{\rm{g}}}}}{{|{r_{\rm{g}}}|}}.{\sin ^{ - 1}}|{r_{\rm{g}}}|. $ | (9) |
应用公式(8)和(9)算得的结果(图 14至图 17)与图 10至图 13相应,但图 17不与图 13相对应,为的是与图 14比较,以便看w的作用;并与图 12比较,看不同的w的效果(虽然u相同,但在冷涌和台风情况下的w可有不同)。

|
图 14 2012年3月23日21:00~22:00冷涌大风时期水滴轨迹的数值模拟结果。rp=70 μm, |

|
图 15 2008年9月24日04:00~05:00飓风眼的前壁大风时期水滴轨迹的数值模拟结果。rp=100 μm, |
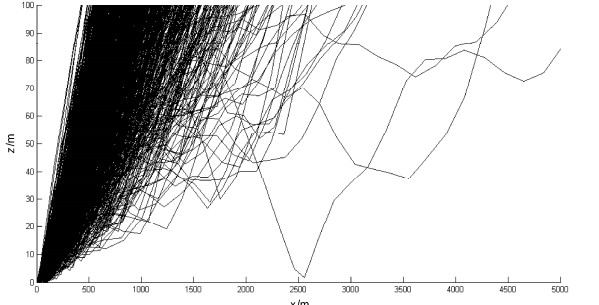
|
图 16 同图 15,但δ ·w = 3 m/s;N1=955,N2=45,N3=0 Figure 16 Same as Fig. 15, except that δ ·w = 3 m/s. N1=955, N2=45, N3=0 |
|
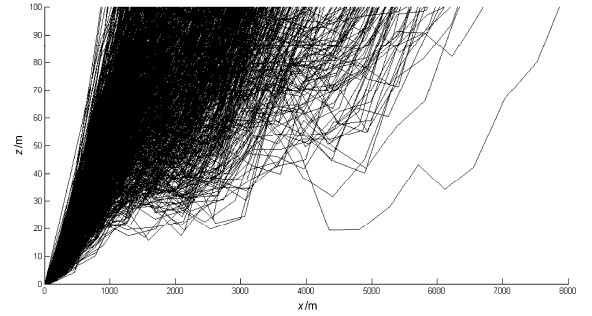
图 17 同图 14,但δ ·w = 0.5 m/s;N1=1000,N2=0,N3=0 Figure 17 Same as Fig. 14, except that δ ·w = 0.5 m/s. N1=1000, N2=0, N3=0 |
我们取
|
表 1 冷涌情况时上升率 |
|
表 2 飓风情况时上升率 |
|
表 3 同表 2,但 |
|
表 4 同表 1,但 |
表 4考虑了垂直速度的作用,比表 1更准确;但因冷涌情况下我们测得的w可能有不小的不确定度,用表 1和表 4哪个更好,尚难确知。只有一点应该指出,表 1给出的是下限(因未考虑到w>0的作用)。
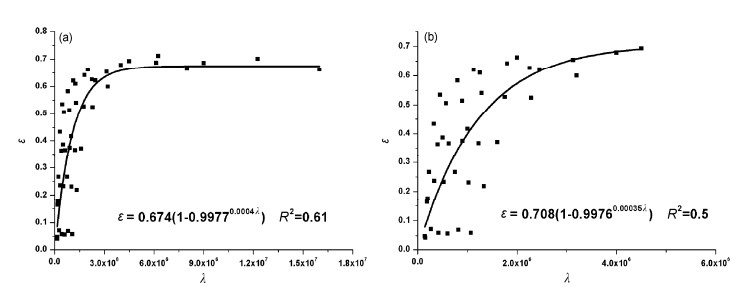
进一步,我们尝试作出
| $ \lambda \equiv {\bar u^2}/({r_{\rm{p}}}g), $ | (10) |
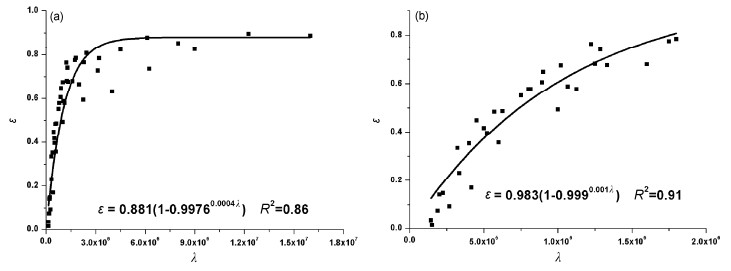
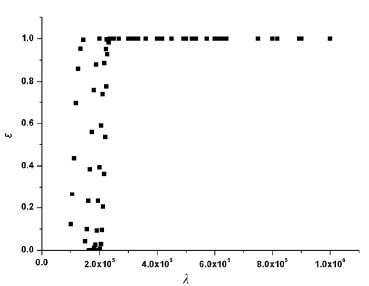
于是可将上面所述的数值模拟结果综合成 ε(rp,u)=ε(λ),点聚图和参数化公式如图 18至图 21。
|
图 18 (a)冷涌情况下的上升率 |

|
图 21 同图 18,但为飓风情况,w由参数化公式给出 Figure 21 Same as Fig. 18, but for typhoon period, w is given by the parameterization formula |
我们对南海上冷涌大风和台风过境期间的大气边界层特性的分析表明:由于风和浪的作用,从海表到至少100 m高度,10 min平均水平风速u基本不随高度而变,且大多还伴有平均上升气流,即w>0;有很强的相干的阵风扰动(频率在1/60~1/600 Hz);而高频(大于1/60 Hz)的湍流脉动则大体上仍属于Kolmogorov的惯性湍流区,其特性及w都可表成以u作参数的参数化公式。
应用Thomson的湍流模式,与粘性流体力学方程耦合,我们计算了破头浪冠射出的各种半径
有一些问题需要说明和进一步澄清:
(1)海气间的能量和物质交换通量,一般都写成是海上10 m高处的平均风速(U10)的函数。而在大风情况下U10其实没有意义,甚至只是虚拟的。从蒲福风力表中注明的海况可知,在8级大风(17.2~20.7 m/s),浪高是5.5 m(一般)到7.5 m(最高);10级狂风(24.5~28.4 m s−1),浪高是9.0 m(一般)到12.5 m(最高);12级飓风(32.7~36.9 m s−1),浪高是14 m(一般)到大于16 m(最高)。不过,我们的观测表明大风期海上大气边界层低层的风速u基本不随高度而变,可以取u权作U10。
(2)在我们的数值模拟中尚未计入水滴在大气中的蒸发,从而半径rp变小,而更易于上升,可见上升率比未考虑蒸发作用时的还应提高。计算水滴的蒸发作用也不难,例如见Edson and Fairall(1994)。但须应用湍流系数,而非静止粘性大气的扩散系数。这样,上升率就还依赖于空气中的相对湿度(RH)以及空气温度Ta和海表水温Ts。
(3)大水滴进入大气后,除蒸发而变小变干成含盐率高的粒子外,还可能发生极其复杂的与大气湍流团的碰撞以及粒子间的相互作用而分裂成小粒子的过程。因此,海盐气溶胶粒径谱分布会与初离浪冠时的水滴谱有很大的不同。由于这些复杂过程难于计算,不妨用大气边界层上层的观测到的谱形,而取总盐量等于全部进入该层的水滴的总盐量。
(4)有上升气流存在的海上大气边界层顶往往很低,而且有云。上升到该处的海盐气溶胶粒子或者成为云滴的凝结核,或者被云滴所吞并,从而不可能继续进入更高的高度,但使总云量增加。其次,还有很多机会(如在风暴和台风等)会碰到下雨,于是这些盐滴气溶胶又作为湿沉降回到洋面上,这些都使进入大气对流层中的海盐气溶胶数量和总盐量比由洋面上发出的大为减少。
Andreas E L. 1998. A new sea spray generation function for wind speeds up to 32 m s−1 [J]. J. Phys. Oceanogr., 28(11): 2175-2184. DOI:10.1175/1520-0485(1998)028<2175:ANSSGF>2.0.CO;2
|
Andreas E L. 2002. A review of sea spray generation function for the open ocean [M]. Atmosphere-Ocean Interactions. Southampton: WTT Press: 1-46.
|
Andreas E L. 2010. Spray-mediated enthalpy flux to the atmosphere and salt flux to the ocean in high winds [J]. J. Phys. Oceanogr., 40(3): 608-619. DOI:10.1175/2009JPO4232.1
|
Andreas E L, Jones K F, Fairall C W. 2010. Production velocity of sea spray droplets [J]. J. Geophys. Res., 115(C12): C12065. DOI:10.1029/2010JC006458
|
Black P G, D'Asaro E A, Drennan W M, et al. 2007. Air-sea exchange in hurricanes:Synthesis of observations from the coupled boundary layer air-sea transfer experiment [J]. Bull. Am. Meteor. Soc., 88(3): 357-374. DOI:10.1175/BAMS-88-3-357
|
Cheng X L, Zeng Q C, Hu F. 2011. Characteristics of gusty wind disturbances and turbulent fluctuations in windy atmospheric boundary layer behind cold fronts [J]. J. Geophys. Res., 116(D6): D06101. DOI:10.1029/2010JD015081
|
Cheng X L, Zeng Q C, Hu F. 2012. Stochastic modeling the effect of wind gust on dust entrainment during sand storm [J]. Chinese Sci. Bull., 57(27): 3595-3602. DOI:10.1007/s11434-012-5230-z
|
Cheng X L, Wu L, Song L L, et al. 2014. Marine-atmospheric boundary layer characteristics over the South China Sea during the passage of strong typhoon Hagupit [J]. J. Meteor. Res., 28(3): 420-429. DOI:10.1007/s13351-014-3279-0
|
Cheng X L, Huang J, Wu L, et al. 2015. Structures and characteristics of the windy atmospheric boundary layer in the South China Sea region during cold surges [J]. Adv. Atmos. Sci., 32(6): 772-782. DOI:10.1007/s00376-014-4228-7
|
Clift R, Grace J R, Weber M E. 1978. Bubbles, Drops, and Particles [M]. New York: Academic Press.
|
Edson J B, Fairall C W. 1994. Spray droplet modeling. I. Lagrangian model simulation of the turbulent transport of evaporating droplets [J]. J. Geophys. Res., 99(C12): 25295-25311. DOI:10.1029/94JC01883
|
Fairall C W, Banner M L, Peirson W L, et al. 2009. Investigation of the physical scaling of sea spray spume droplet production [J]. J. Geophys. Res., 114(C10): C10001. DOI:10.1029/2008JC004918
|
Jaeglé L, Quinn P K, Bates T S, et al. 2010. Global distribution of sea salt aerosols:New constraints from in situ and remote sensing observations [J]. Atmos. Chem. Phys., 11(7): 3137-3157. DOI:10.5194/acp-11-3137-2011
|
Kolmogorov A N. 1962. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number [J]. J. Fluid Mech., 13(1): 82-85. DOI:10.1017/S0022112062000518
|
Massel S R. 2007. Ocean Waves Breaking and Marine Aerosol Fluxes [M]. Berlin, Germany: Springer.
|
Monin A S, Yaglom A M. 1975. Statistical Fluid Mechanics [M]. Cambridge: MIT Press: 605pp.
|
Mueller J A, Veron F. 2009a. A sea state-dependent spume generation function [J]. J. Phys. Oceanogr., 39(9): 2363-2372. DOI:10.1175/2009JPO4113.1
|
Mueller J A, Veron F. 2009b. A Lagrangian stochastic model for heavy particle dispersion in the atmospheric marine boundary layer [J]. Bound.-Layer Meteor., 130(2): 229-247. DOI:10.1007/s10546-008-9340-8
|
Mueller J A, Veron F. 2014. Impact of sea spray on air-sea fluxes. Part Ⅰ:Results from stochastic simulations of sea spray drops over the ocean [J]. J. Phys. Oceanogr., 44(11): 2817-2834. DOI:10.1175/JPO-D-13-0245.1
|
Petelski T, Piskozub J, PaplińSka-Swerpel B. 2005. Sea spray emission from the surface of the open Baltic Sea [J]. J. Geophys. Res., 110(C10): C10023. DOI:10.1029/2004JC002800
|
Thomson D J. 1987. Criteria for the selection of stochastic models of particle trajectories in turbulent flows [J]. J. Fluid Mech., 180: 529-556. DOI:10.1017/S0022112087001940
|
Veron F, Hopkins C, Harrison E, et al. 2012. Sea spray spume droplet production in high wind speeds [J]. Geophys. Res. Lett., 39(16): L16602. DOI:10.1029/2012GL052603
|
Zeng Q C, Cheng X L, Hu F, et al. 2010. Gustiness and coherent structure of strong winds and their role in dust emission and entrainment [J]. Adv. Atmos. Sci., 27(1): 1-13. DOI:10.1007/s00376-009-8207-3
|
Zhang J A, Black P G, French J R, et al. 2008. First direct measurements of enthalpy flux in the hurricane boundary layer:The CBLAST results [J]. Geophys. Res. Lett., 35(14): L14813. DOI:10.1029/2008GL034374
|
赵栋梁. 2012. 海洋飞沫及其对海-气相互作用影响的研究进展[J]. 地球科学进展, 27(6): 624-632. Zhao Dongliang. 2012. Progress in sea spay and its effects on air-sea interaction (in Chinese)[J]. Adv. Earth Sci. (in Chinese), 27(6): 624-632. DOI:10.1029/2005JC002960
|
Zhao D L, Toba Y, Sugioka K I, et al. 2006. New sea spray generation function for spume droplets [J]. J. Geophys. Res., 111(C2): C02007.
|
 2018, Vol. 42
2018, Vol. 42