大家自然要问,全球大气运动怎么会和拓扑联系在一起?这还是要从天气图谈起。地面天气图给出的高压、低压实际上是空间压力曲面的廓线。空间压力曲面是非常不均匀的,有的地方压力高,有的地方压力低。这就像地形一样,有高山、洼地和平原,全球压力的曲面是一个坑坑洼洼的球面,气象学家绘制等压线在地面天气图上,从地面天气图上等压线的斑图就可以认识到空间压力曲面的形状,所以地面天气图上等压线是空间压力曲面的廓线。同样,高空天气图上等高线是绘制的该压力曲面的廓线,由于静力关系
每天的天气图不同,说明空间压力曲面凸凹不平的位置不断发生变化,就好像一个橡皮泥球,通过伸长缩短的挤压,扭转等变换(不允许断裂),不断变换橡皮泥的形状一样,拓扑学就是研究这种变换下的不变性质(Richeson,2008)。拓扑上已经说明,球面的不变量称为球面的欧拉示性数(Euler characteristic),它的数是2。从物理学上讲全球空气是连续相通的,压力场在某个地方洼下去,其他地方必然要鼓起来,它们不会离开地球球面,球面是一个整体,所以从整体上看大气运动,必须要全球来考虑,不能将空气割裂开来,因而全球压力曲面的拓扑不变量是研究天气变化所必须掌握的,大气科学家不但要知道,大气运动要遵循流体力学的纳维-司托克斯方程,全球大气运动还要遵循拓扑定理。
2 压力曲面及其临界点的典型形式、天气图的廓线三维空间的曲面通常可表示成隐式形式:
| $ f(x, y, z) = 0 $ | (1) |
若公式(1)中的z写
| $ p = p(x, y) $ | (2) |
公式(2)也是压力曲面在天气图上的廓线。
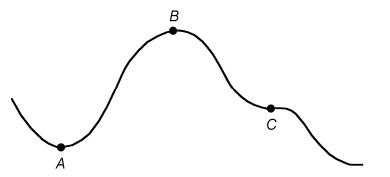
对于一维地形曲线
|
图 1 一维地形曲线 Figure 1 One-dimensional topographic curve |
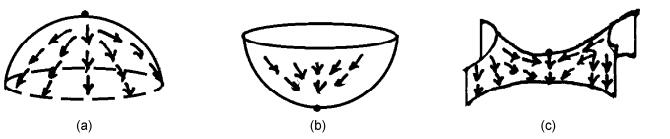
对于二维压力曲面,常见三种形式见图 2。此时的能量函数
|
图 2 三种压力曲面及其临界点 Figure 2 Three types of pressure surfaces and their critical points |
| $ \left\{ \begin{array}{l} p(x, y) = - {x^2} - {y^2}, \\ p(x, y) = {x^2} + {y^2}, \\ p(x, y) = - {x^2} + {y^2}, \end{array} \right. $ | (3) |
其中,
| $ \partial p/\partial x = 0;{\rm{ }}\partial p/\partial y = 0. $ | (4) |
若天上下雨,雨经过这三个临界点,雨流动的向量场见图 3中箭头的方向。为了区分这三种临界点,莫尔斯(Morse,1929)追踪临界点处不稳定方向的数目
|
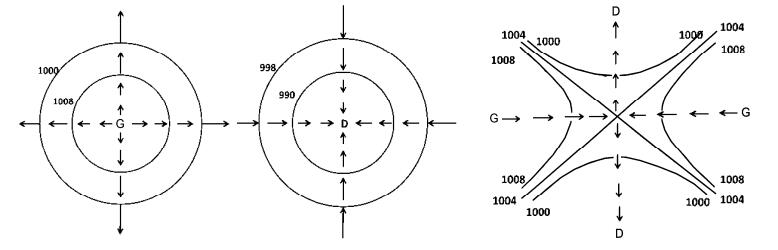
图 3 三种曲面在天气图上的廓线(实线为等压线,数字单位为hPa,小箭头代表雨水流动方向) Figure 3 Curves on the synoptic weather chart corresponding to the three types of surfaces. Solid lines are isobars, units: hPa; small arrows show the flowing directions of rain |
对于图 2的三种曲面,它们在天气图上的等压线廓线见图 3。图 3中小箭头的方向是由高值等压线指向低值等压线(垂直于等压线)的气压梯度力方向(气压梯度是由低的等压线指向高的等压线),所以可以认为图 3种小箭头所代表的风向是仅有气压梯度力的情况。
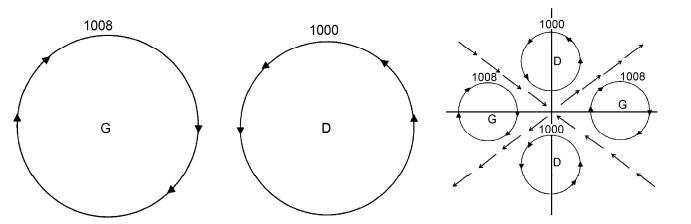
若再加上一个科里奥利力,使气压梯度力和科氏力相平衡形成地转风,则风向就沿着等压线吹,北半球的情况见图 4。
|
图 4 气压梯度力和科氏力平衡下的等压线廓线(实线)及其风向(小箭头) Figure 4 Isobars (solid lines) under the balance condition of pressure gradient force and Coriolis force |
图 3、图 4中的高压中心、低压中心和鞍点对应图 2中的三个临界点。所以三种压力曲面及其临界点和天气图上的高压、低压、鞍形场及其高压中心,低压中心以及鞍点是完全对应的。
3 临界点指数、莫尔斯定理和庞加莱-霍普夫定理压力曲面是球面,无论如何变换,它仍是球面,只是凸凹不平的位置发生变化。若仅受气压梯度力作用,速度场由公式(3)分别可以写成
| $ \begin{array}{l} \left\{ \begin{array}{l} \dot x = u = 2x = - \partial p/\partial x, \\ \dot y = v = 2y = - \partial p/\partial y, \end{array} \right.{\rm{ }}\left\{ \begin{array}{l} \dot x = u = - 2x = - \partial p/\partial x, \\ \dot y = v = - 2y = - \partial p/\partial x, \end{array} \right.{\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} \dot x = u = 2x = - \partial p/\partial x, \\ \dot y = v = - 2y = - \partial p/\partial y, \end{array} \right. \end{array} $ | (5) |
按照公式(4),速度场公式(5)右端为零的点
为了区分梯向量场的三种奇点,莫尔斯用指数
莫尔斯证明了如下定理(Morse,1929):如果闭合曲面的孤立临界点是由源点、汇点和鞍点构成,那么闭合曲面的欧拉示性数为
| $ χ=(源点数目)+(汇点数目)-(鞍点数目), $ | (6) |
对压力曲面是球面而言χ=2。
由于源点数目就是高压的数目,汇点数目就是低压数目,所以公式(6)就变成天气图上的如下表述:
| $ (高压中心点数目)+(低压中心的数目)-\\~~~~~~~~~~~~~(鞍点数目)=2. $ | (7) |
庞加莱和霍普夫将莫尔斯定理推广到闭合曲面上的任何向量场(奇点指标不限于±1),说明若在闭合曲面上仅有有限个奇点(无风点),那么所有这些奇点的指标之和等于闭合曲面的欧拉示性数:
| $ \chi = \mathop \sum \limits_{i = 1}^n {I_n} $ | (8) |
公式(8)对于球面而言χ = 2。
在地面天气图上,流场只绘制高压和低压,鞍点就不绘出,更谈不上绘出像偶极子奇点(I=2)流场了,但庞加莱-霍普夫定理[公式(8)]是一个普遍成立的定理。
4 全球大气流场的实例本节我们举若干全球流场的例子,说明莫尔斯定理以及庞加莱-霍普夫定理的应用。
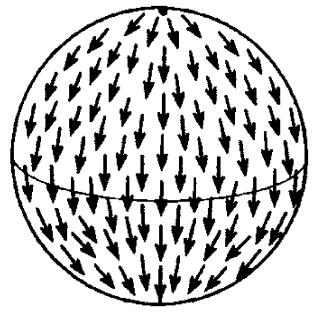
4.1 从北极沿经圈流向南极的经向流图 5显示的全球流场。从图 5看出,北极点是一个源,南极点是一个汇,按公式(6)χ=1+1-0=2,遵循莫尔斯定理。
|
图 5 沿经圈的经向流 Figure 5 Meridional flow along the longitudes |
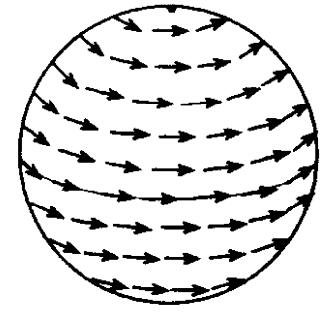
流场见图 6。从图 6看出,北极点上是一个低压中心,南极点是一个高压中心,按公式(7)χ=1+1-0=2,遵循莫尔斯定理和庞加莱-霍普夫定理。
|
图 6 沿纬圈的西风环流 Figure 6 Westerly flow along the latitudes |
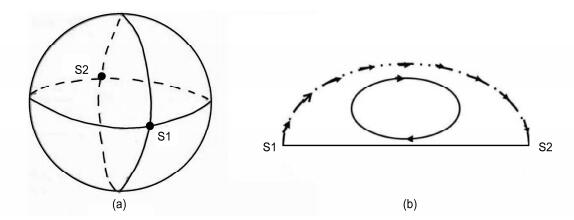
我们设想,从北极到南极沿经圈剖一刀,再沿赤道剖一刀,将地球分成四个部分(图 7)。这四个部分的球表面各有一个涡旋流场,赤道大圆和北极,南极间经圈有两个交点,它们是鞍点S1和S2。这样,北半球和南半球各有两个涡旋,它们是高低压中心(注意:南半球的低压中心是顺时针旋转)高低压中新的奇点指标均为1,鞍点的指标是-1,故根据公式(8)有(2×1)+(2×1)+[(2×(-1)]=2仍遵循球面的拓扑定理。
|
图 7 (a)北极—南极经圈和赤道将地球分成四部分;(b)每个部分在两个鞍点S1和S2间形成涡旋的剖面 Figure 7 (a) Four parts of the earth surface divided by the equator and a longitude circle; (b) cross section along two saddle points (S1, S2) where the vortex |
前面三个例子只是球面上的流场,并未涉及垂直流场。下面两个例子是大家熟悉的单圈环流和三圈环流。它们均和球面流场有关,因为只有球面是低压流场,它才能辐合产生上升运动,若球面是高压流场,下沉运动到球面才能使空气水平辐散。
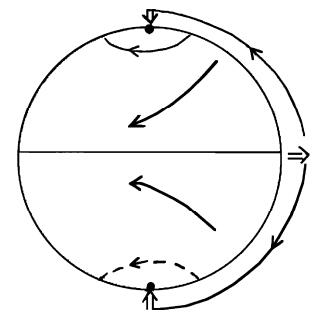
该环流是从赤道热空气上升到高空,在高空冷空气流向两极(北极和南极)。因此从地面讲,在南极和北极都是高压中心,见图 8。
|
图 8 单圈环流地表面流场 Figure 8 Surface flow corresponding to single-cell circulation |
北半球的流场围绕北极作顺时针旋转是高压,南半球的南极空气作逆时针旋转,仍是高压。南北极之间是东风带,由于科氏力,北半球形成东北信风,南半球形成东南信风。此时地表面的两个奇点都是高压中心,没有鞍点,高压中心的指标均是+1,根据公式(7)1+1-2=2,仍遵循拓扑定理。
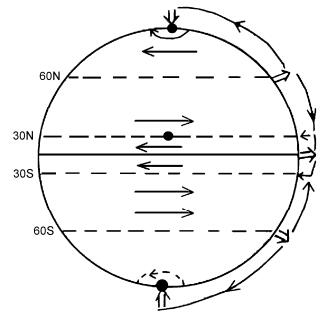
4.5 三圈环流(Djuric,1994)单圈环流是很少出现的,赤道上升的空气,在向北极南极流动中由于受科氏力的作用在南北纬30°左右下沉并形成常见的西风带见图 9。
|
图 9 三圈环流中的地表东西风带 Figure 9 Surface westerlies and easterlies corresponding to the three-cell circulations |
这样地表东西风带交错,但不形成孤立奇点,赤道极地间形成三圈环流奇点仍在南北极,它们都是高压,和4.4节单圈环流一样,仍遵循拓扑定理[公式(7)]。
4.6 偶极子流场最后我们举一个例子,全球只有一个奇点的偶极子流场(图 10),见图 10。和前面5个例子不同,这种风场奇点的指标是+2,它遵循庞加莱-霍普夫定理[公式(8)]

|
图 10 球只有一个奇点的偶极子流场 Figure 10 Global dipole flow with only one singular point |
地表天气图上的等压线斑图主要是高低压中心及鞍点,而高空天气图上的等高线斑图主要以波动为主,且高空摩擦力小,流场沿等压线吹,北半球背风而立,高度高低的等压线在右,如何寻找流场奇点呢?
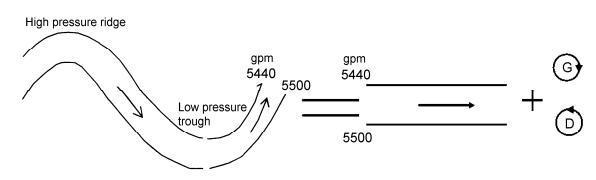
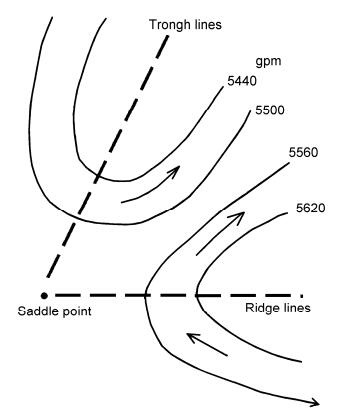
首先,我们注意到波动的等高线斑图等价于平直等高线加上高压涡旋或低压涡旋,见图 11。这样波动流场的奇点,高压脊和低压槽就相当于高压中心和低压中心。高压脊是极大点,指标为-1,低压槽是极小点,指标为+1。其次,至于鞍点,由于高空图上并不绘制它,但是至少一个槽线和一个脊线的交点便是鞍点,见图 12。
|
图 11 500 hPa天气图上等高线波动等于平直等高线加上高压或低压 Figure 11 Geopotential perturbations at 500-hPa synoptic weather chart are equal to straight isohypses plus high or low pressure |
|
图 12 一个高压脊线和一个低压槽线的交点便是鞍点 Figure 12 The point of intersection between a high pressure ridge line and a low pressure trough line is the saddle point |
天气图上高压低压,以及高低压间的鞍形场的斑图是空间压力曲面的廓线,高低压中心及鞍点对应于空间压力曲面的临界点。空间压力曲面是凸凹不平的球面,尽管凸凹不平的位置不断变化,但压力球曲面的欧拉示性数位2是不变的。在天气图上,高压个数加上低压个数,再减去鞍点个数应等于2,这是拓扑上的庞加莱-霍普夫定理,全球大气运动还要遵循这个拓扑定理。
Bluestein H B. 1992. Synoptic-Dynamic Meteorology in Midlatitudes:Volume Ⅰ. Principles of Kinematics and Dynamics [M]. New York, Oxford: Oxford University Press: 431pp.
|
Bluestein H B. 1993. Synoptic-Dynamic Meteorology in Midlatitudes. Volume Ⅱ. Observations and Theory of Weather Systems [M]. Oxford: Oxford University Press: 594pp.
|
Djuric D. 1994. Weather Analysis [M]. Prentice-Hall Inc.: 314pp.
|
Flegg H G. 1974. From Geometry to Topology [M]. New York: Crane Russak and Co.: 275pp.
|
Hatcher A. 2002. Algebraic Topology [M]. Cambridge: Cambridge University Press: 345pp.
|
Hopf H. 1926. über die curvatura integra geschlossener hyperflächen [J]. Math. Ann., 95(1): 340-367. DOI:10.1007/BF01206615
|
刘式达, 刘式适, 傅遵涛. 2016. 大气运动的几何和拓扑[M]. 北京: 高等教育出版社. Liu Shida, Liu Shishi, Fu Zuntao. 2016. Geometry and Topology of Atmosphere Motions (in Chinese)[M]. Beijing: Higher Education Press.
|
Morse M. 1929. Singular points of vector fields under general boundary conditions [J]. Amer. J. Math., 51(2): 165-178. DOI:10.2307/2370703
|
Poincaré H. 1902. Sur certaines surfaces algébriques, Troisième complément à l'Analysis sitûs [J]. Bull Soc. Math. France, 30: 49-70. DOI:10.24033/bsmf.657
|
Richeson D S. 2008. Euler's Gem:The Polyhedron Formula and the Birth of Topology [M]. Princeton, NJ: Princeton University Press: 368pp.
|
 2018, Vol. 42
2018, Vol. 42

