2 成都信息工程大学大气科学学院/高原大气与环境四川省重点实验室/气候与环境变化联合实验室, 成都 610225
3 中国科学院大学地球科学学院, 北京 100049
4 南京信息工程大学大气科学学院, 南京 210044
2 School of Atmospheric Sciences/Plateau Atmosphere and Environment Key Laboratory of Sichuan Province/Joint Laboratory of Climate and Environment Change, Chengdu University of Information Technology, Chengdu 610225
3 College of Earth Sciences, University of Chinese Academy of Sciences, Beijing 100049
4 College of Atmospheric Sciences, Nanjing University of Information Science & Technology, Nanjing 210044
厄尔尼诺—南方涛动(ENSO)现象是发生在热带太平洋地区的厄尔尼诺(El Niño)和南方涛动(Southern Oscillation)现象的合称,是气候系统中具有最强年际变率信号的一种短期气候现象。ENSO是热带太平洋地区海气相互作用的结果(Philander, 1983; Ropelewski and Halpert, 1987; Wang and Picaut, 2004; Weng et al., 2007; Kao and Yu 2009),但它对全球的天气和气候事件异常皆具有重要影响(Bjerknes, 1969; Cane, 1983; Rasmusson and Wallace, 1983; Hoerling et al., 1997; Trenberth et al., 1998; Alexander et al., 2002; McPhaden et al., 2006; Ham et al., 2014)。因此,成功预测ENSO具有重要意义。
El Niño事件通常呈现最大的海表温度暖异常中心在热带东太平洋。然而,自20世纪90年代以来,区别于传统厄尔尼诺事件的一种新型El Niño事件开始频繁发生,该类El Niño事件最大海表温度暖异常中心位于热带中太平洋。根据海表温度暖中心位置的不同,上述两类El Niño通常被称为东太平洋型El Niño事件和中太平洋型El Niño事件(EP-El Niño事件和CP-El Niño事件,Kao and Yu 2009)。两类El Niño事件发生的周期与物理机制具有显著差异(Kug et al., 2009, 2010; Weng et al., 2007; Xiang et al., 2013),而且对全球天气和气候的影响也存在较大差别(Feng et al., 2011; Taschetto and England, 2009; Weng et al., 2007; Zhang et al., 2011; Wang and Wang, 2013)。所以,采用数值模式预报ENSO事件时,不仅需要预报El Niño事件是否发生,还需提前对El Niño事件的类型做出判断,因而更增加了ENSO预测的挑战性。
自热带海洋与全球大气计划(TOGA)实施以来,科学家们提出多种理论解释ENSO现象的物理机制,并发展了不同复杂程度的数值模式模拟、预报ENSO事件。ENSO事件的预报技巧已得到明显提高,但就ENSO预报结果而言,ENSO预测仍具有很大的不确定性(Kirtman et al., 2001; Wang and Picaut, 2004; Wang and Fiedler, 2006; Chen and Cane, 2008; Jin et al., 2008; Qi et al., 2017)。尤其,CP-El Niño事件频繁发生,而许多模式又未能较好模拟该类事件,从而进一步加剧了ENSO预测的不确定性(Hendon et al., 2009; Hu et al., 2012; Jeong et al., 2012; Xue et al., 2013)。
许多研究针对ENSO预测开展了大量的可预报性研究工作,对影响ENSO预报技巧的因素进行了深入探讨。许多文献从预报误差增长的角度研究ENSO的可预报性。例如,Moore and Kleeman(1996)从误差增长的角度揭示了ENSO预测的“春季可预报性障碍”(SPB)现象,强调了初始误差的作用;Chen et al.(2004)则通过改进数值模式的初始化程序,减弱了ENSO事件的SPB现象,提高了ENSO的预报技巧。Mu et al.(2007a, 2007b)进一步强调具有特定空间结构的初始误差能够导致ENSO预测产生更大的预报误差(Duan et al., 2009; Duan and Wei, 2013; Duan and Hu, 2016; Hu and Duan, 2016)。这些结论主要针对传统的EP-El Niño事件。近来,Tian and Duan(2016)采用校正的Zebiak-Cane模式(Zebiak and Cane, 1987)也强调了初始误差对CP-El Niño预测不确定性具有重要影响;而且,他们对比了EP-和CP-El Niño的具有特定结构的最快增长初始误差,表明两类El Niño事件具有空间结构相似的最快增长初始误差,但该两类初始误差却更多的导致EP-El Niño发生SPB现象。Hendon et al.(2009)通过回报试验指出Niño4指数的预报不存在明显的SPB现象,从而也说明CP-El Niño较EP-El Niño的SPB现象更弱,也意味着CP-El Niño比EP-El Niño更易预报。Luo et al.(2008)通过计算观测和模式预报的距平相关系数指出,Niño4指数的预测水平比Niño3指数更高,同样也表明CP-El Niño可能比EP-El Niño更容易预报。Luo et al.(2008)的结果基于SINTEX-F模式(Scale Interaction Experiment Frontier coupled GCM, Luo et al., 2003, 2005),该模式的模式误差很小,是国际上模拟ENSO效果最好的模式之一,而Tian and Duan(2016)的结果是基于完美模式假设。所以,结合他们的结果可以推断,当模式误差的影响可以忽略时,CP-El Niño比EP-El Niño更容易预报。事实上,无论何种情形,这些研究都强调了初始场的精度在两类El Niño预测中的重要性。可见,ENSO预报不确定性的主要原因之一是数值模式中初始误差的增长。因此,对初始状态的准确估计为提高两类El Niño事件的预报技巧提供了最有前途的途径。
要提供更准确的初始场,方法之一是增加额外的观测。这一思想可以追溯到美国1947年开始的飓风监测计划(Riehl et al., 1956)。该思想随后也被应用到关于气候预测研究的海洋观测计划中,如世界气候研究计划(WCRP)分别于1985年和1990年启动的Tropical Ocean and Global Atmosphere(TOGA)计划和World Ocean Circulation Experiments(WOCE)。但是,由于观测资料的有效利用取决于具体的天气和气候过程,而且大范围的增加观测不仅耗费金钱,还难以实施。理论上,如果在初值的敏感区同化观测资料,初始场的改善会更加有效地改进模式的预报效果;而在初值的其他区域同化观测资料,初始场的质量不会明显地改进或对模式预报效果不产生任何积极影响,甚至可能对整个预报效果产生负面影响。于是,Riehl et al.(1956)提出了目标观测的思想,即通过对小范围“关键区域”加密观测并同化到初始分析场,便可达到大范围增加观测对预报水平的提高程度(Snyder, 1996;Mu, 2013)。而且,关于数值天气预报的研究表明,在资料缺乏、模式较为简单的情况下,不论是用何种同化方案,相对于简单的在某些固定地点增加观测,目标观测对预报效果的提高更加有效(Fischer et al., 1997;Morss et al., 2001)。
目标观测已经在高影响天气预报外场试验中得到实施(Langland et al., 1999; Wu et al., 2007)。进入21世纪以来,目标观测也已成为世界气象组织倡导的一项新的国际大气科学计划,即观测系统研究与可预报性试验(THORPEX)的主要研究内容之一。数值天气预报主要是数值模式的初值问题(Lorenz, 1963;丑纪范和郜吉东,1995;Kalnay,2002),初始场的不确定性是数值天气预报的主要误差来源之一,因而利用目标观测改进初始场,提高数值天气预报水平,是具有深厚理论基础的。对于ENSO预测,如前所述,大量研究已经表明,初始误差是ENSO预报结果不确定性的主要误差来源之一。因此,应用于改进数值天气预报研究的目标观测方法有可能为改进ENSO数值预报模式的初始场提供一条有效途径(Mu et al., 2007a, 2007b; Duan et al., 2009; Yu et al., 2009)。事实上,一项新的热带太平洋观测计划[Tropical Pacific Observing System 2020(TPOS20),Cravatte et al., 2016]正在研究和部署。该项计划希望在原TOGA观测网的基础上,优化热带太平洋观测网,用以应对两类El Niño事件的研究和预测。那么,究竟如何优化热带太平洋观测网?该问题与目标观测的研究紧密相关。
目标观测的关键在于目标观测区域(或称敏感区)的确定,这直接影响目标性观测的有效性。目前,用于确定目标观测敏感区的方法大致可以分为两类(Toth and Kalnay, 1997; Bishop and Toth, 1999; Baker and Daley, 2000; Bishop et al., 2001; Hamill and Snyder, 2002):第一类是从初始误差发展的角度出发,通过不同的方法获取对预报结果影响最大的初始误差,然后把误差较大且集中的区域确定为敏感区;第二类则是直接以减小预报结果不确定性为目标,即考察同化哪个区域的观测资料,能够最大程度减小预报结果的不确定性,那么该区域即为目标观测敏感区。前者确定敏感区的方法主要有线性奇异向量(Palmer et al., 1998)、繁殖向量(Lorenz and Emanuel, 1998)、梯度敏感性(Langland and Rohaly, 1996),和近来我国学者提出的条件非线性最优扰动方法(Mu et al., 2003; Duan and Mu, 2009),等等,该类方法将最快增长初始误差的大值区作为敏感区;后者则包含集合卡尔曼滤波、集合转换卡尔曼滤波方法(Bishop et al., 2001)等,此类方法逐点同化观测,将能够导致预报结果不确定性具有最大减小程度的格点区域作为敏感区。
集合卡尔曼滤波和集合转换卡尔曼滤波都是基于状态空间贝叶斯估计具体实现的算法,他们要么采用线性近似观测算子且观测误差服从高斯分布,要么对预报误差协方差采取线性近似。考虑到该类方法的上述局限性,Kramer and Dijkstra(2013)利用粒子滤波同化方法(KD),将模式的集合样本看做系统状态的样本,利用序贯重要性采样方法同化不同区域的观测,然后计算同化后集合样本的离散度较同化前的减小程度,确定目标观测敏感区(详见第二节)。尽管集合离散度也是考察预报结果不确定性的一种度量,但如果集合样本不能较好描述集合平均的不确定性的话,对应的集合预报系统就是不可靠的,上述目标观测就不能有效减小集合预报的离散度,以及实际预报中希望知道的集合平均预报误差,从而使得由集合离散度度量的初值敏感性不能得到实际预报的验证(详见第三节)。那么,如何解决粒子滤波目标观测方法集合离散度和集合平均预报误差不一致的问题?即是说,如何改进KD的目标观测方法,使其集合离散度和集合平均预报误差度量的初值敏感性一致,或者说,使改进的KD方法确定的目标观测敏感区的有效性能够得到实际预报的验证?
本文将针对该问题,提出一种可以解决上述矛盾的新的粒子滤波目标观测方法,并将其应用于两类El Niño的目标观测问题研究,从而为新的热带太平洋观测计划TPOS20提供可供参考的,且具有深厚理论基础的优化观测方案。文章第二节将针对KD目标观测方法的局限性,提出新的粒子滤波目标观测方法;第三节介绍研究所采用的试验方案和资料,第四、五节则分别针对中太平洋型和东太平洋型El Niño事件,对比新、旧方法确定的目标观测敏感区及其在提高El Niño预报技巧中的作用;最后,文章给出总结和讨论。
2 基于粒子滤波同化的目标观测新方法如前所述,粒子滤波—目标观测方法采用资料同化思想确定敏感区,即考察在哪一个区域实施目标观测,且通过资料同化系统同化该观测,能够最大程度减小预报结果的不确定性。本节将在考察KD的粒子滤波—目标观测方法局限性的基础上,提出可克服该局限性的新的粒子滤波—目标观测方法。
2.1 粒子滤波同化方法粒子滤波是利用蒙特卡洛算法实现贝叶斯滤波的一种同化方法。该同化方法根据系统状态向量的经验条件分布,在状态空间产生一组随机样本(即粒子)集合,然后根据已有的观测信息不断调整粒子的权重和位置,用调整后的粒子信息修正原始的经验条件分布,得到新的样本集合。当样本容量很大时,这种蒙特卡洛描述近似于状态变量真实的后验概率分布。该同化方法的核心是利用序贯重要性采样(Sequential Importance Sample,SIS)方法来获取粒子的权重(Van Leeuwen, 2009),其理论模型如下:
设状态向量Xk的发展由以下模型给出:
| $ {\mathit{\boldsymbol{X}}_{k + 1}} = {\mathit{\boldsymbol{M}}_k}\left({{\mathit{\boldsymbol{X}}_k}, {\mathit{\boldsymbol{\zeta }}_k}} \right), $ | (1) |
其中,Xk是t=tk时的状态向量,Mk是模式传播算子,ζk是均值为0的白噪声序列,t=tk时刻的观测记为Yk。资料同化的目的是为了在已知当前及过去所有时刻的观测
| $ {p_N}\left({{\mathit{\boldsymbol{X}}_k}} \right) = \sum {w_k^i} \delta \left({{\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{X}}_k^i} \right), $ | (2) |
其中,wki代表粒子权重,δ(·)表示一个函数,该函数在除了零以外的点函数值都为零,在整个定义域上的积分等于1。每个粒子的初始状态是从状态向量的初始概率密度分布p(X0)中均匀采样(w0i=1/N)得到的。在粒子滤波方法中,pN(Xk|Y1:k)是经过预测和更新递归得到的。假设已知t=tk-1时刻的后验概率密度pN(Xk-1|Y1:(k-1)),也就是说粒子的状态Xk-1i和权重wk-1i已知,在t=tk时刻,我们得到了此时的观测Yk。在预测步,每一个粒子Xk-1i向前积分得到下一个时刻的粒子状态Xki,则在给定t=tk时刻以前所有观测Y1:(k-1)的前提下,t=tk时刻系统状态的后验条件概率密度函数pN(Xk|Y1:(k-1))可表示为
| $ {p_N}({\mathit{\boldsymbol{X}}_k}|{\mathit{\boldsymbol{Y}}_{1:\left({k - 1} \right)}}) = \sum\limits_{i = 1}^N {w_{k - 1}^i} \delta ({\mathit{\boldsymbol{X}}_k} - \mathit{\boldsymbol{X}}_k^i), $ | (3) |
在更新步,由Bayes原理可计算当前时刻的条件概率密度函数:
| $ {p_N}\left({{\mathit{\boldsymbol{X}}_k}|{\mathit{\boldsymbol{Y}}_{1:k}}} \right) = \frac{{p({\mathit{\boldsymbol{Y}}_k}|{\mathit{\boldsymbol{X}}_k}){p_N}({\mathit{\boldsymbol{X}}_k}|{\mathit{\boldsymbol{Y}}_{1:\left({k - 1} \right)}})}}{{p({\mathit{\boldsymbol{Y}}_k})}}, $ | (4) |
由(3)、(4)式可得到粒子新的权重,即
| $ w_k^i = \frac{{p({\mathit{\boldsymbol{Y}}_k}|\mathit{\boldsymbol{X}}_k^i)}}{{p({\mathit{\boldsymbol{Y}}_k})}}w_{k - 1}^i, $ | (5) |
其中,公式(5)等号右边的分子表示给定系统状态Xki的前提下,观测Yk的概率密度,它和观测误差的概率分布直接相关。假设观测误差为一多元正态分布,其协方差矩阵为∑,则
| $ p({\mathit{\boldsymbol{Y}}_k}|\mathit{\boldsymbol{X}}_k^i) - \exp \left\{ { - \frac{1}{2}{{\left[ {{\mathit{\boldsymbol{Y}}_k} - \mathit{\boldsymbol{H}}\left({\mathit{\boldsymbol{X}}_k^i} \right)} \right]}^{\rm T}}\sum {^{ - 1}\left[ {{\mathit{\boldsymbol{Y}}_k} - \mathit{\boldsymbol{H}}\left({\mathit{\boldsymbol{X}}_k^i} \right)} \right]} } \right\}, $ | (6) |
其中,H为观测算子,将状态向量空间投影到观测空间。经过更新步得到了新的粒子及其权重后,继续进行预测步,直至过程结束。
2.2 粒子滤波同化预报技巧的度量:Predictive Power指数在利用粒子滤波方法同化了观测后,我们可以得到系统状态概率密度分布的蒙特卡洛描述,而这个分布通常是非高斯的。采用基于信息熵的Predictive Power指数(Schneider and Griffies, 1999, PP指数)来度量同化了观测后的非高斯的系统状态概率分布相对于气候态概率分布不确定性的减小程度。记随机变量X的概率密度函数为p(X),则PP指数(PP)可以表示为
| $ {P_{\rm{P}}} = 1 - \exp (- {S_{q\left(X \right)}} + {S_{p\left(X \right)}}), $ | (7) |
其中,Sp(X)是随机变量的信息熵,用于度量X的概率密度函数所包含的不确定性的大小。
| $ {S_{p\left(\mathit{\boldsymbol{X}} \right)}} = - \kappa \int {p\left(\mathit{\boldsymbol{X}} \right)} \ln p\left(\mathit{\boldsymbol{X}} \right){\rm{d}}\mathit{\boldsymbol{X, }} $ | (8) |
其中,Sq(X)是q(X)的熵,代表该气候态概率分布的不确定性,q(X)代表变量X气候态分布的概率密度函数。κ是一个决定熵的单位的常数,此处取为1。当随机变量的每一个可能值出现的概率相同时,它的熵最大;而当随机变量只有一个可能值时,熵最小。
利用粒子滤波同化方法,可以得到由粒子(即集合样本)描述的系统状态概率密度函数p(Xk|Y1:k)的近似估计,进一步可求得该集合样本的熵。如果一个集合预报的概率密度函数等于气候态的概率密度函数,则该集合预报的Predictive Power等于零,即相对于气候态分布,该集合预报并没有对变量提供提高预报技巧的额外信息。如果一个集合预报的熵减小(如通过同化观测信息使熵减小),则其PP指数值增大,即通过同化,集合预报技巧提高了。由PP指数的定义可以看出,0≤PP≤1;PP指数值越大,预报结果不确定性减小程度越大。
2.3 基于粒子滤波的目标观测新方法如引言所述,KD的粒子滤波—目标观测方法,将模式的集合样本看作系统状态的样本,利用序贯重要性采样方法同化不同区域的观测,计算同化结束时集合样本的预报不确定性较同化前的减小程度,来确定目标观测敏感区。在该方法中,KD所采用的预报不确定性的度量是集合样本离散度,而用PP指数表征同化的观测在减小预报不确定性中的重要性。PP指数的大值区,即意味着同化该区域的观测,由集合离散度度量的预报结果不确定性的减小程度最大。KD称该区域为目标观测敏感区。那么,该敏感区的敏感性是否可以在预报试验中得到验证呢?
对于KD方法,目标观测敏感区的验证,即是在同化阶段同化敏感区的观测,确定集合样本的权重,然后考察预报阶段集合预报不确定性的减小程度。也就是说,KD目标观测敏感区的验证是通过集合预报试验。对于集合预报,Branković et al.(1988)表明,一个可靠的集合预报系统的集合平均预报误差应该约等于集合成员与集合平均的均方离散度。KD目标观测方法仅考量在同化结束时,同化哪个区域的观测使得集合离散度减小程度最大,未同时考察是否使得集合平均预报误差有效减小,因此其涉及的集合预报在同化阶段就很难保证是一个可靠的集合预报系统,通过同化KD确定的目标观测也很难保证更有效地减小预报时间段的集合离散度以及集合平均预报误差。那么,如何使同化窗口内集合样本的离散度和集合平均预报误差的减小程度一致,从而保证所得到的目标观测敏感区能够通过集合预报的有效性检验?
尽管一个可靠的集合预报系统的集合平均预报误差应该约等于集合成员与集合平均的均方离散度,但这是在完美模式假定下得到的理论结果,在实际中不一定能达到。在实际应用中,通常是考虑集合平均预报误差和集合离散度的相关关系。对于一个合理的集合预报系统,两者之间应该存在较强的正相关关系,即集合离散度减小的同时,集合平均误差也减小,且减小程度相当,这样的集合预报系统才是合理的。因此,为了使KD的用集合离散度度量的敏感区,同时能够通过集合预报离散度和集合平均预报误差的检验,我们可通过三个步骤获得新的目标观测敏感区:
(1)计算同化结束时集合样本离散度和集合预报误差呈现较强正相关的区域;
(2)在该正相关区域,用粒子滤波同化不同区域观测计算系统状态变量的信息熵;
(3)根据上述信息熵,计算PP指数值,将PP指数大值区作为目标观测敏感区。
该三步骤即描述了本文提出的新的粒子滤波目标观测方法。可以看出,新粒子滤波—目标观测方法区别于原方法之处在于提前确定了集合离散度和集合预报误差呈现较强正相关的区域,从而理论上保证了新粒子滤波—目标观测方法确定的敏感区可以同时通过集合离散度和集合平均预报误差的检验。
3 试验方案和资料粒子滤波同化需要选取足够样本估计预报不确定性的减小程度,因此在试验过程中需要多次积分数值模式,以获取更多的集合样本,这无疑带来巨大的计算量。另一方面,由于模式误差的存在,天气和气候事件的目标观测敏感区的确定可能会依赖数值模式,而客观存在的敏感区不受任何因素的影响。因此,为了使我们确定的敏感区尽可能地接近客观敏感区,可采用多模式的结果,从而尽可能消除模式误差的影响,得到更加可信的目标观测敏感区。多模式的结果也为目标观测敏感区的计算提出了挑战。那么,如何克服上述困难得到更加可信的目标观测敏感区呢?
如引言所述,本文关注两类El Niño事件预测的热带海温目标观测敏感区,而目标观测敏感区是一个初值问题,因此,目标观测敏感区需考察预报结果对初值的敏感性。理论上,对于一个给定的气候数值模式,如果外强迫不随时间变化,那么在数值模式长期积分中,把某一年的状态作为真值,其他年份作为对该年份的预报,那么其预报误差则由两个年份初始状态的差别所导致,即该预报误差仅由初始误差导致(Zhang et al., 2015)。对于两类El Niño事件,我们采用耦合模式比较计划第五阶段(CMIP5)中九个模式工业革命前控制试验(Pre-industrial control)对热带海表温度(SST,20°S~20°N,120°E~80°W)的模拟结果(表 1)。该试验中的温室气体等外强迫始终维持在工业革命前的水平,即不考虑外强迫因子随时间的变化,或者说数值模式结果只反映模式的内部变率。在这些模式长期积分的时间序列中,分别选取大量El Niño年作为“真值”,将各模式长期积分的其他年份作为对该真值的预报。这样,每一次El Niño年就可以有大量集合预报样本,而且由于外强迫不变,这些集合预报样本的预报误差仅由初始误差导致。对于粒子滤波同化使用的观测,本文采用理想观测,即在上述从模式积分中选取的真值El Niño年的相关状态变量上叠加随机误差,得到理想观测。对于每一次真值El Niño年及其集合预报样本,通过粒子滤波同化上述理想观测,赋予集合预报样本(或粒子)不同的权重,滤掉权重较小的样本并重采样,得到新的集合样本。
| 表 1 九个CMIP5模式及其数据长度和发生的EP-El Niño/CP-El Niño次数。模式资料源于https://esgf-node.llnl.gov/search/cmip5/[2017-10-30] Table 1 The data length of nine CMIP5 models and numbers of the simulated EP-El Niño (Eastern Pacific El Niño)/CP-El Niño (Central Pacific El Niño). The model data were downloaded from the website https://esgf-node.llnl.gov/search/cmip5/ [2017-10-30] |
利用新的集合预报样本,计算同化窗口结束时集合平均关于“真值”的预报误差和集合样本关于集合平均的均方离散度,以及它们的相关系数(记为R)。另外,我们知道,未同化观测的集合预报样本可以理解为是对气候态的估计或预报,据此可以计算同化窗口结束时气候态的信息熵,而由同化观测后得到的新的集合预报样本可以计算集合预报成员在同化窗口结束时的信息熵。利用这两个信息熵,计算PP指数值的空间分布。将PP指数的空间分布作用于R,然后将R大于某一阈值的区域中的PP指数大值区确定为ENSO预测的目标观测敏感区。
对于本研究关心的两类El Niño事件,该研究采用Kug et al.(2009)关于两类厄尔尼诺事件的区分标准,即如果Niño3指数和Niño4指数至少有一个在北半球冬季(NDJ)大于0.5℃,且Niño3指数小于(大于)Niño4指数,即认为该年发生了CP-El Niño事件(EP-Niño事件)。按照该标准,考察表 1中九个CMIP5模式长期积分的模拟结果,选择典型的El Niño事件,即选择在春季开始增暖,冬季达到峰值的所有El Niño事件作为研究对象。各模式长期积分中存在的CP-El Niño事件和EP-El Niño事件次数见表 1。由表 1可知,除了CNRM-CM5、GFDL-ESM2M、GISS-E2-R和CCSM4模式外,其他模式模拟得到的CP-El Niño事件过少。因此,该研究探讨CP-El Niño的目标观测敏感区仅选择上述四个模式的资料。对于EP-El Niño事件的模拟,表 1中九个模式的模拟均能得到较多的个例,所以探讨EP-El Niño事件的目标观测敏感区采用表中所有模式。
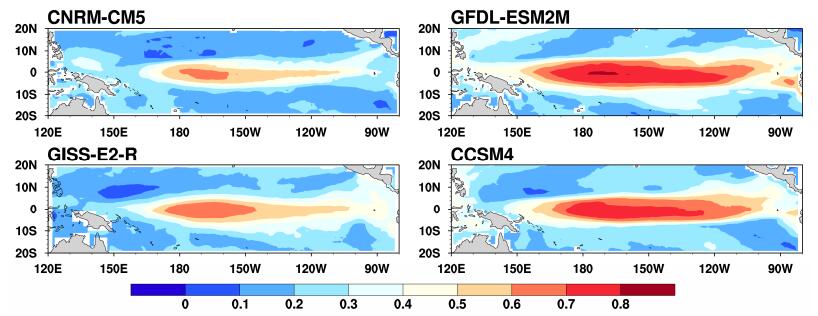
4 中太平洋型厄尔尼诺事件的目标观测敏感区对于上述选取的能够较好模拟CP-El Niño事件的4个模式:CNRM-CM5、GFDL-ESM2M、GISS-E2-R和CCSM4模式,针对长期积分的时间序列中的每一次CP-El Niño事件及其对应的集合预报样本,采用第三节的试验方案,即用粒子滤波方法同化1~3月份热带太平洋各个格点上的月平均SST观测,对原样本赋予权重,滤掉权重较小的样本并重采样,得到新的样本,考察新集合样本和原集合样本在3月份的信息熵,即可得到PP指数值(详见第二节KD方法)。图 1分别给出了用KD方法计算得到的四个模式中CP-El Niño事件的PP指数值空间分布。结果表明,对于上述四个模式来说,同化不同格点SST观测后得到的PP指数值的分布总体上相似,即PP指数值相对较大的区域主要位于赤道附近约170°E~120°W的中东太平洋。
|
图 1 CNRM-CM5、GFDL-ESM2M、GISS-E2-R和CCSM4模式中,用KD方法计算的CP-El Niño的PP指数的集合平均 Figure 1 Ensemble means of the PP (Predictive Power) index calculated by the KD approach for CP-El Niño in the models of CNRM-CM5, GFDL-ESM2M, GISS-E2-R and CCSM4, respectively |
该研究也通过同化其他季节的观测,考察确定CP-El Niño的PP指数值空间分布特征,即通过同化CP-El Niño年上一年度10~12月、CP-El Niño年的4~6月和7~9月的SST观测,考察哪个区域的SST观测对未来El Niño预报不确定性的减小程度最有效。结果表明,各模式所得到的PP指数空间分布与图 1类似。也就是说,无论从哪个季节开始预报CP-El Niño事件,对于四个模式,PP指数的大值区均主要位于热带中东太平洋。PP指数的大值区即意味着同化该区域的观测能够更大程度的减小集合离散度度量的预报结果的不确定性。如果考察能够最大程度减小集合离散度度量的预报结果的不确定性,那么对应的最大PP指数则主要位于赤道中太平洋。根据Kramer and Dijkstra(2013)的观点,热带中太平洋即代表了CP-El Niño事件的目标观测敏感区。那么,该敏感区的敏感性能否能够通过CP-El Niño预报试验的检验呢?
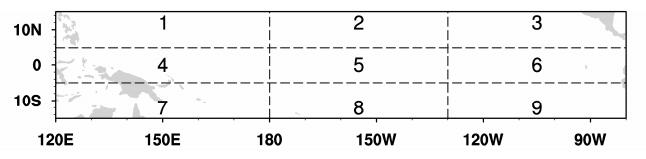
为了验证KD方法确定的目标观测敏感区是否是CP-El Niño事件预测的目标观测敏感区,我们针对上述四个模式,同化了图 1中PP指数最大的前M个格点上1~3月期间的SST观测,再让得到的Niño4指数的加权集合自由发展9个月,从而得到对CP-El Niño事件的一次集合预报。根据不同模式不同的PP指数大小,M值的选取也不同。具体地,在同化SST时,CNRM-CM5模式取M=60,其余三个模式均取M=80。同时作为对照,该研究也选取其他三个随机区域,考察了同化该区域相同格点数观测的集合预报结果。每个模式随机区域的选取方法如下:首先,将热带太平洋区域(15°S~15°N,120°E~80°W)平均分成9部分(如图 2所示)。对于每个模式,分别从赤道以北的1、2、3区域,赤道区域的4、5、6区域,以及赤道以南的7、8、9区域中,各随机选出一个区域,并随机选取该区域内M个格点的方阵,记为Rand1、Rand2和Rand3区域。随机区域的选取共实现10次,以下对应于随机区域的结果为10次随机区域实现的集合平均。
|
图 2 热带太平洋区域(15°S~15°N,120°E~80°W)均分为9个区域的示意图 Figure 2 Diagram of the equally-shared nine regions over the tropical Pacific Ocean (15°S–15°N, 120°E–80°W) |
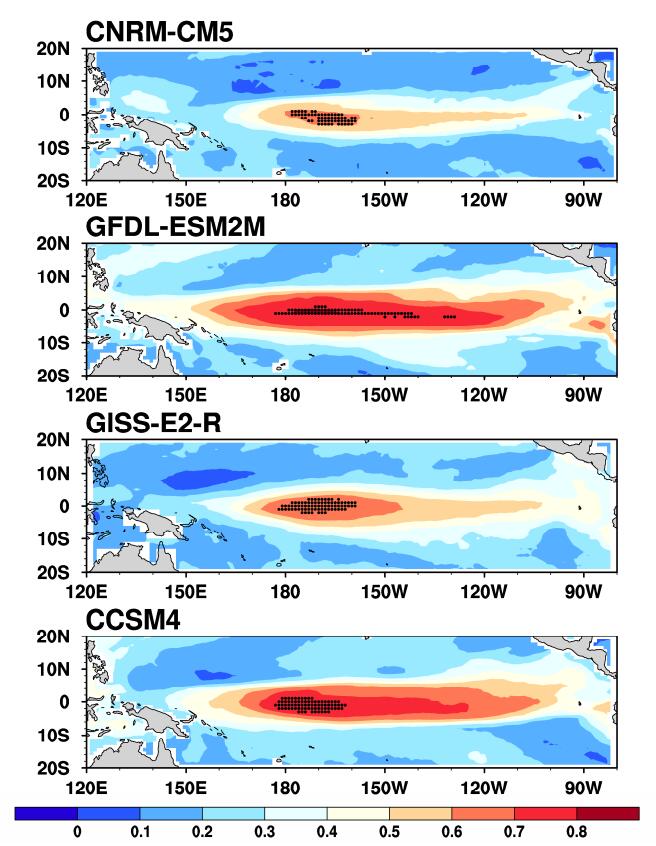
图 3给出了CNRM-CM5、GFDL-ESM2M、GISS-E2-R和CCSM4模式用KD方法计算的PP指数最大值前M个格点的位置(记为PP_max),主要位于日界线附近的赤道中太平洋,即上述表明的用KD方法确定的CP-El Niño事件的目标观测敏感区。对每个模式,我们分别同化PP_max和随机区域Rand1、Rand2和Rand3区域的上述M个格点1~3月的SST观测,考察对CP-El Niño事件Niño4指数4~12月集合预报的预报不确定性的减小程度,从而考察目标观测敏感区的有效性。
|
图 3 同图 1,图中黑色打点区域是各模式PP指数最大值前M个格点(CNRM-CM5模式选取前60个格点,GFDL-ESM2M、GISS-E2-R和CCSM4模式均选取前80个格点)所在的位置 Figure 3 As in Fig. 1, but with black-dotted regions for the first M grid points with much large PP values (the first 60 grid points are for model CNRM-CM5 while the first 80 grid points are for models GFDL-ESM2M, GISS-E2-R, and CCSM4) |
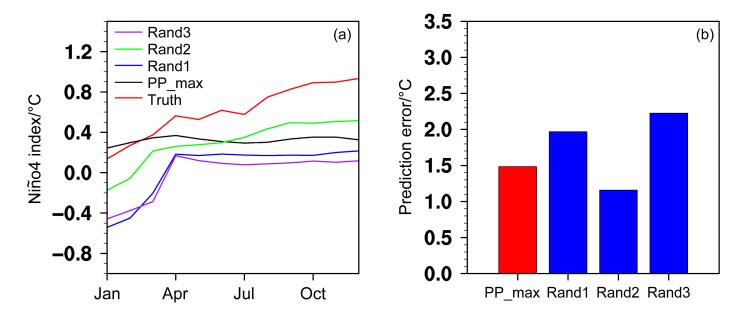
图 4给出了CCSM4模式中的一次CP-El Niño事件预测的目标观测敏感区试验结果。从图中可看出,对于该事件,同化1~3月PP_max区域观测的SST后,该次CP-El Niño事件4~12月的集合平均预报误差明显小于同化Rand1和Rand3区域内观测的SST集合平均预报误差,但略大于同化Rand2区域观测的SST预报误差。但是无论同化哪个区域观测的SST,CCSM4模式都未能预报出该次CP-El Niño事件;从Niño4指数的发展来看,同化PP_max区域观测的SST得到的CP-El Niño事件的预报也仅在同化阶段1~3月与真值最接近,而在预报阶段4~12月却远离真值,造成较大的预报误差,甚至大于同化Rand2区域观测的SST预报误差。所以,与同化随机区域观测的SST预报结果相比,同化PP_max区域内观测的SST并未有效提高该次CP-El Niño事件的预报技巧。那么,是否KD方法确定的赤道中太平洋区域不是CP-El Niño事件预报的目标观测敏感区呢?为此,我们进一步针对更多的个例进行目标观测敏感区试验。具体地,随机选取CCSM4模式中的15次CP-El Niño事件,分别同化图 3所示的PP_max,以及随机选取的Rand1、Rand2和Rand3区域的前M个观测格点,考察对CP-El Niño事件Niño4指数预报不确定性的减小程度。图 5给出了上述15次事件的集合平均预报误差。结果表明,对于大多数CP-El Niño事件,同化PP_max区域内观测的SST相较于同化其他三个随机区域观测的SST并未有效减小Niño4指数的集合平均预报误差。
|
图 4 (a)CCSM4模式中一次CP-El Niño事件(红线)的Niño4指数,及其同化PP_max区域观测的SST(黑线)和随机区域Rand1、Rand2和Rand3区域观测的SST(蓝线、绿线、紫线)的集合平均预报的Niño4指数;(b)a图中集合平均预报的预报误差 Figure 4 (a) Niño4 index of a CP-El Niño event (red line) in the model CCSM4, its ensemble-mean forecast by assimilating the observed SST over the PP_max region (black line), and over three randomly selected regions denoted by Rand1, Rand2, and Rand3 (blue, green, and purple lines). (b) Prediction errors of the ensemble-mean forecasts shown in Fig. a |
|
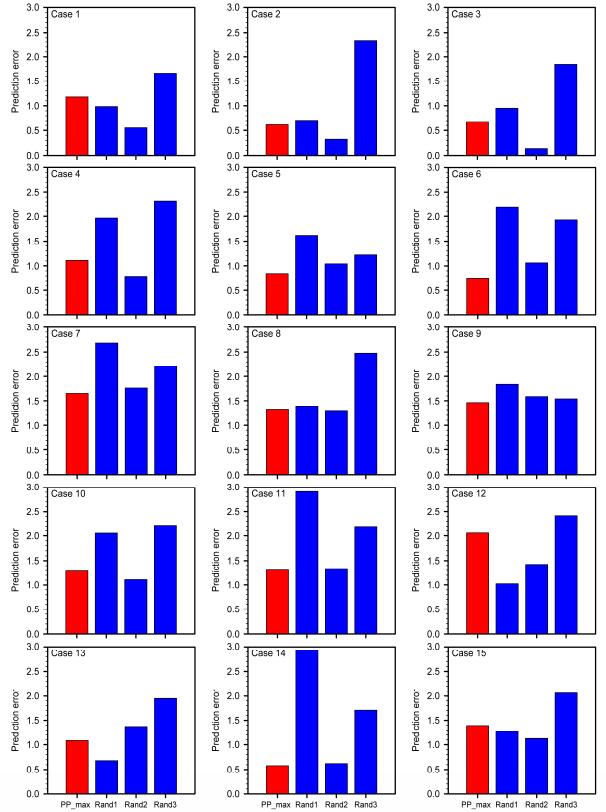
图 5 CCSM4模式中的15个CP-El Niño个例的集合平均预报误差,其中包含同化PP_max(红色柱状)观测的SST集合预报,以及同化Rand1、Rand2和Rand3区域(蓝色柱状)内观测的SST集合预报 Figure 5 Ensemble-mean forecast errors for the selected fifteen CP-El Niño events simulated by model CCSM4, including the forecasts with assimilation of the observed SST in the PP_max region (red bar) and in three randomly selected regions denoted by Rand1, Rand2, and Rand3 (blue bars) |
上述结果是针对CCSM4模式的结果。如图 3所示,其他三个模式也得到了与CCSM4类似的目标观测敏感区,那么是否该敏感区在其他三个模式预报中可以得到检验呢?事实上,我们通过目标观测敏感区试验,同样表明了与随机区域相比,同化上述目标观测敏感区SST观测而得到的CP-El Niño事件的集合预报,并不是具有最小集合平均预报误差的预报,即是说,PP_max区域不能代表CP-El Niño事件预测的目标观测敏感区,而且不同模式均表明了这一点,说明该敏感区的敏感性未能通过有效性检验的原因不是来自于模式,而是来自于KD方法的局限性,即KD方法只保证了其确定的目标观测使集合预报离散度减小程度最大,而不能同时确保集合平均预报误差显著减小(详见第二节)。事实上,在KD方法确定的目标观测敏感区的检验中,主要涉及的是用粒子滤波同化目标观测,赋予集合样本不同权重而开展的集合预报。对于一个给定的完美模式,集合预报技巧的高低依赖于集合样本的选取,而对于该研究使用的粒子滤波方法,集合样本的选取是否合理就归结为通过粒子滤波同化赋予样本的权重,上述同化PP_max观测未能有效减小集合平均预报误差,说明赋予集合样本的权重不合理。也就是说,粒子滤波同化的观测不合理,而这恰恰说明只用集合离散度度量集合预报的不确定性是KD方法的局限性。那么究竟应该同化哪个区域的观测可以使得集合预报样本得到更加合理的权重,从而使得集合样本离散度显著减小的同时,集合平均预报误差也大大减小?
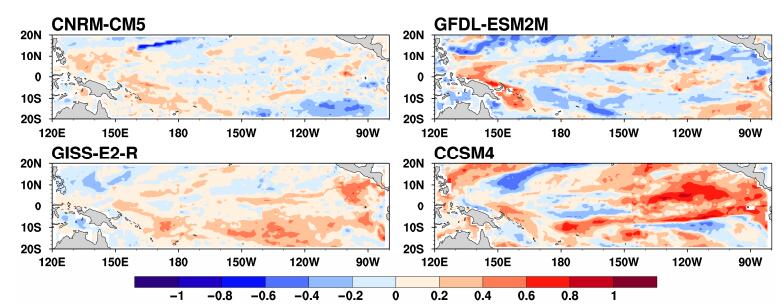
为克服KD方法的局限性,本文第二节考虑到集合预报系统可靠性的衡量标准,结合集合离散度和集合预报误差度量的相关关系,提出了粒子滤波目标观测新方法。以下我们将使用新的目标观测方法确定CP-El Niño的目标观测敏感区。事实上,新的目标观测方法只是在KD方法的基础上,根据粒子滤波同化的结果,提前确定了集合样本离散度与集合平均预报误差间呈现较强正相关的区域,然后在该区域计算PP指数,确定能够更大程度减小集合离散度的目标观测区域,从而保证了目标观测在最大程度减小集合离散度的同时,也能够更大地减小集合平均预报误差。具体地,对于上述能够较好模拟CP-El Niño事件的4个模式(CNRM-CM5、GFDL-ESM2M、GISS-E2-R和CCSM4模式),针对每一次CP-El Niño事件及其对应的集合预报样本,用粒子滤波方法同化1~3月份热带太平洋各个格点上的月平均SST观测,根据每个样本所赋予的权重的大小,通过重采样得到新的集合样本,计算此时各个格点对应的集合样本离散度与集合平均误差的相关系数(图 6),然后在呈现较强正相关的区域计算PP指数值,选取PP指数最大值的前M个格点区域(CNRM-CM5模式选取前60个格点,GFDL-ESM2M、GISS-E2-R和CCSM4模式均选取前80个格点)作为目标观测敏感区。
|
图 6 CNRM-CM5、GFDL-ESM2M、GISS-E2-R和CCSM4模式同化1~3月观测的SST后,所得到的Niño4指数的集合离散度和集合平均误差的空间相关系数 Figure 6 Correlation coefficients between ensemble spread and ensemble-mean forecast errors for the ensemble forecasts generated by models CNRM-CM5, GFDL-ESM2M, GISS-E2-R, and CCSM4 with assimilation of observed SST observations from January to March |
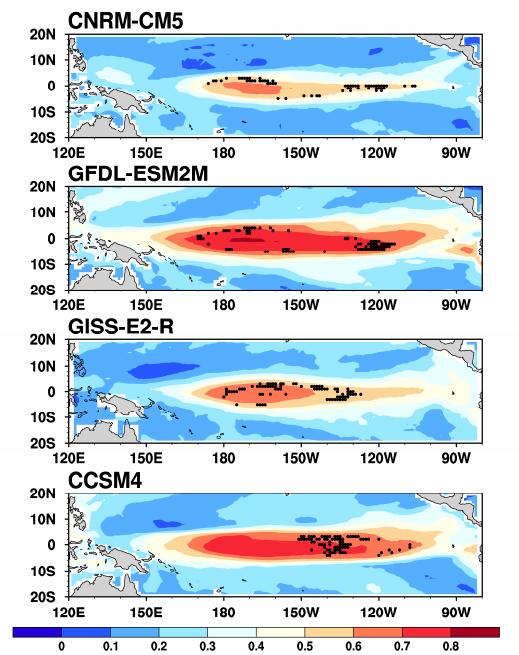
图 7给出了上述四个模式关于CP-El Niño预测的目标观测敏感区,其中黑色打点区域即为PP指数值最大的前M个格点的位置,记为PP_max_R,即为新方法确定的目标观测敏感区。从图中可以看出,黑色打点的区域较KD方法确定的敏感区更加分散,且有相当一部分格点的位置在赤道东太平洋。也就是说,新方法确定的敏感区与原方法存在较大差别,新方法除了强调赤道中太平洋目标观测在CP-El Niño预测中的重要性,同时还强调了赤道东太平洋目标观测的必要性。
|
图 7 同图 3,但为新方法计算的PP指数的集合平均 Figure 7 As in Fig. 3, but for ensemble means of the PP index calculated by the new approach |
与KD方法类似,对于新方法,我们也通过同化其他季节的观测,考察确定CP-El Niño的目标观测敏感区。结果表明,各模式所得到的目标观测敏感区分布与图 7类似。所以,无论从哪个季节开始预报CP-El Niño,对集合预报样本离散度和集合平均预报误差的减小具有最大贡献的SST观测可能位于相同的区域,尤其除了赤道中太平洋区域外,也同时强调了赤道东太平洋区域的重要性。另外,我们也注意到,当同化不同季节观测时,只有同化7~9月的观测所得到的PP指数在数值上大于在其他季节同化的结果。事实上,造成该结果的主要原因是由于7~9月一般是El Niño事件发展放大的季节,此时El Niño的信号显著地大于气候噪声,从而使得同化该季节的观测信息能够更大程度地减小El Niño事件集合预报的不确定性。
既然从不同季节开始预报CP-El Niño,SST的目标观测敏感区均主要位于赤道中太平洋和东太平洋,那么这样的敏感区是否可以克服原敏感区的局限性而有效提高CP-El Niño的预报技巧呢?
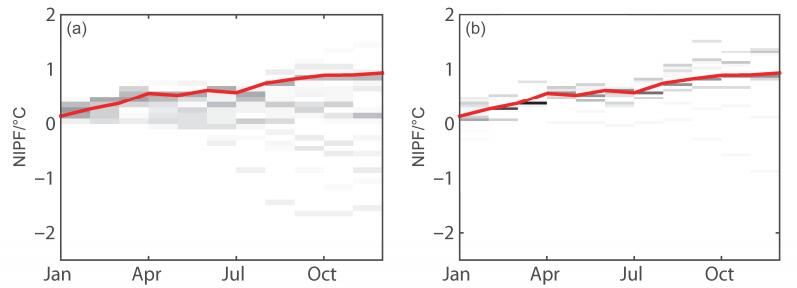
我们仍以图 4中所呈现的CCSM4模式的CP-El Niño事件为例,考察同化PP_max_R区的SST观测后得到的Niño4指数的概率预报,并与KD方法同化PP_max区SST观测作对比(图 8)。结果表明,与同化PP_max区的SST观测相比,同化PP_max_R区的SST观测不仅在同化阶段有效降低了集合预报样本的离散度,而且在预报阶段,也使得大部分集合样本集中在真值CP-El Niño事件附近,具有较小的集合离散度,从而使得同化PP_max_R区的SST观测较同化PP_max区的SST观测具有更小的集合平均预报误差,因而PP_max_R区具有更强的敏感性,即是说同化PP_max_R的SST观测,较同化PP_max的SST观测能够更大程度提高CP-El Niño事件的预报技巧,前者比后者更适合代表CP-El Niño事件的目标观测敏感区。
|
图 8 图 4中CCSM4模式的CP-El Niño的Niño4指数的概率预报:(a)模式同化了PP_max的观测SST后;(b)同化PP_max_R的观测SST后。红线代表真值CP-El Niño事件,灰色区域代表概率预报结果 Figure 8 Niño4 index of probability forecast (NIPF) in the CP-El Niño by model CCSM4 shown in Fig. 4: (a) Assimilation of observed SST in the PP_max region; (b) assimilation of observed SST in the PP_max_R region. Red lines represent the truth values, the areas shaded in gray represent the results of probability forecast |
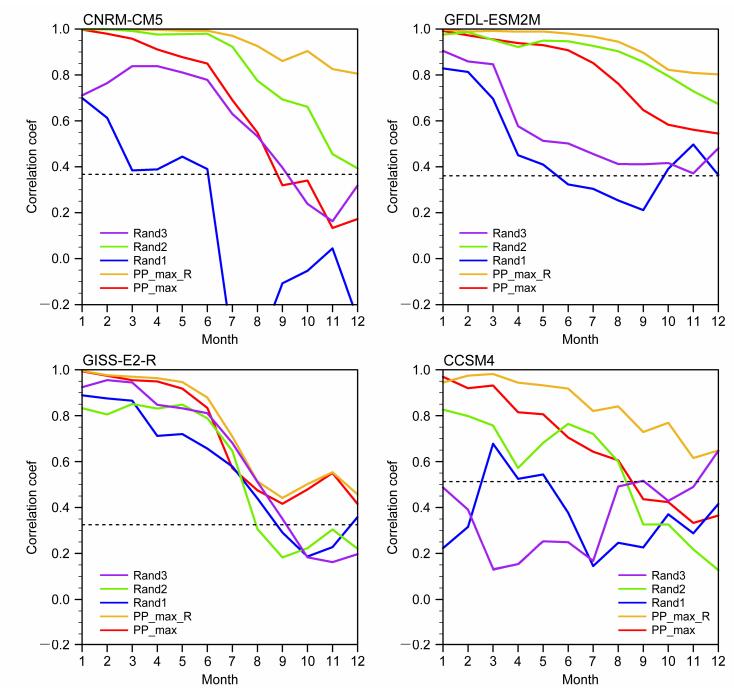
为进一步表明PP_max_R的敏感性,文中也对图 5中所呈现的CCSM4模式的15个CP-El Niño个例进行了新旧敏感区对照试验。结果表明,同化PP_max_R的SST观测,相比同化PP_max的SST观测,能够成功预测出CP-El Niño事件的发生,且大多数个例的集合平均预报误差明显降低。另外,该研究也针对四个模式的所有CP-El Niño个例,给出了同化PP_max_R、PP_max和三个随机区域SST观测后对Niño4指数的集合平均预报与“真值”的相关系数(图 9)。四个模式的结果均表明,与集合平均预报误差类似,同化新方法确定的敏感区PP_max_R的SST观测,较同化KD方法的目标观测敏感区PP_max的SST观测,所得到的集合平均预报具有与真值更高的相关系数,且明显高于同化随机区域观测所得到的相关系数。该结果说明,新方法确定的目标观测敏感区,即赤道中太平洋和东太平洋区域的确是预报CP-El Niño事件的目标观测敏感区,同化该区域的观测相比于同化其他区域观测,更加有利于CP-El Niño集合预报技巧的提高。
|
图 9 对CNRM-CM5、GFDL-ESM2M、GISS-E2-R和CCSM4模式中所有CP-El Niño个例,在分别同化PP_max_R(黄)、PP_max(红)和其他三个随机区域(蓝、绿、紫)观测的SST后,关于其Niño4指数集合平均预报的结果与“真值”的相关系数。图中虚线表示通过置信水平为95%的显著性检验的临界值 Figure 9 Correlation coefficients between the predicted Niño4 index for CP-El Niño events and that of true events. The predicted Niño4 index is obtained by conducting ensemble-mean forecast with assimilation of observed SST in the PP_max_R (yellow), PP_max (red) regions, and other randomly selected three regions (blue, green, and purple), respectively, using models CNRM-CM5, GFDL-ESM2M, GISS-E2-R, and CCSM4. The dashed lines denote significance correlation at the 95% confidence level |
对于EP-El Niño事件,该研究采用的九个模式都具有较好的模拟能力,且在其长期积分中存在较多的EP-El Niño事件(如表 1)。为探讨该类事件的目标观测敏感区,本文考察表 1中所有模式的EP-El Niño事件。与上节探讨的CP-El Niño事件类似,该节也采用KD方法和本文提出的新方法识别EP-El Niño事件的目标观测敏感区,即将表 1中的各数值模式的EP-El Niño事件作为“真值”,将具有定常外强迫的数值模式长期积分(即PI-control试验)的其他年份作为对该事件的集合预报样本(或粒子),则该事件的预报误差则由初始误差导致。对于该事件,利用粒子滤波方法同化1~3月的观测,对原集合样本赋予不同权重,放弃权重较小的样本,然后进行重采样得到新的样本。对于KD方法,直接利用El Niño事件的原样本和新样本的信息熵计算PP指数,将PP指数空间分布中的大值区作为El Niño事件的目标观测敏感区;而对于本文提出的新方法,则首先计算原样本的集合离散度和集合平均误差的空间相关,再在呈现正相关的区域计算PP指数,将PP指数的大值区作为目标观测敏感区。
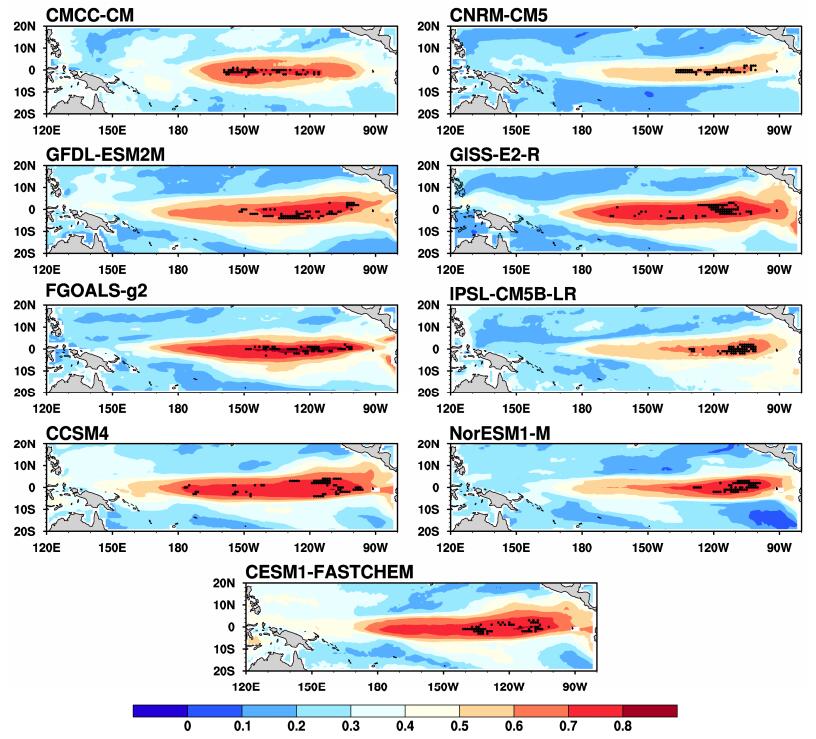
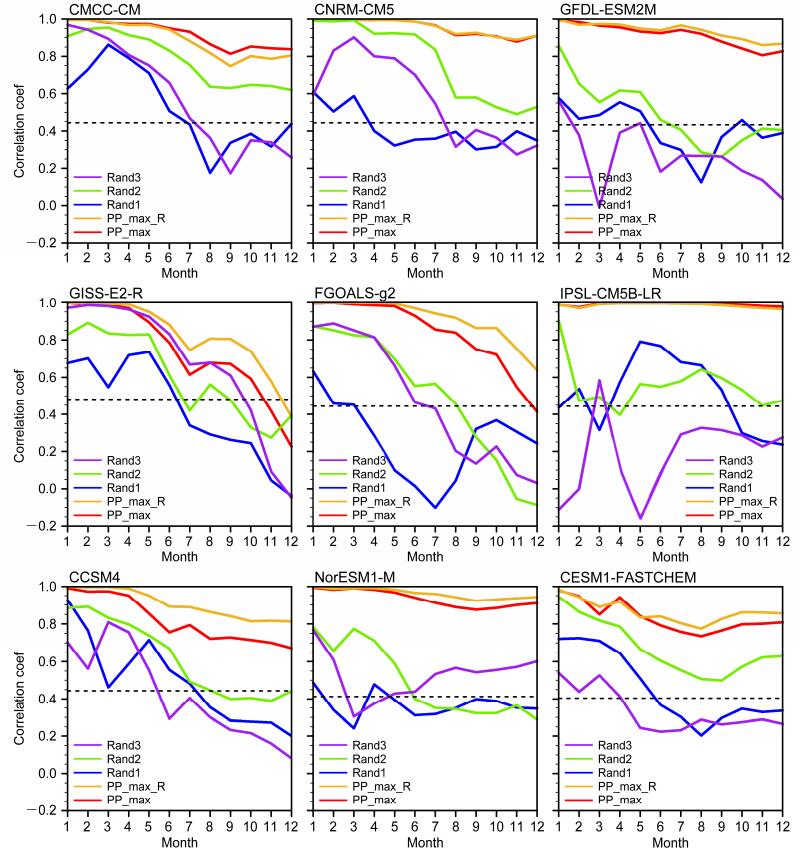
通过计算各模式EP-El Niño事件的PP指数,并考察其大值区作为目标观测敏感区,结果表明,KD方法确定的敏感区主要位于120°W以东,而新方法确定的目标观测敏感区的相当一部分格点则倾向于西移,并接近150°W(图 10),而且新目标观测敏感区的敏感性在EP-El Niño事件4~12月期间的集合预报得到了有效验证。事实上,新敏感区与KD方法确定的敏感区以及随机选取的具有相同格点的区域相比,无论是集合平均预报误差(与图 5类似,故略),还是Niño3指数演变的相关系数(图 11),同化新敏感区目标观测的集合预报都倾向于具有更高的预报技巧。所以,新方法确定的PP指数大值区更适合作为EP-El Niño事件的目标观测敏感区。
|
图 10 用新方法计算得到的表 1中各数值模式EP-El Niño个例的PP指数空间分布的集合平均,打点区域是PP指数最大值的前M个格点 Figure 10 Ensemble means of the PP index calculated by the new approach for the EP-El Niño cases in each model listed in Table 1. The black-dotted regions are for the first M grid points with much large PP values |
|
图 11 表 1中每个模式中所有EP-El Niño个例,在分别同化PP_max_R(黄色线)、PP_max(红色线)和其他三个随机区域(蓝色线、绿色线、紫色线)观测的SST后,对Niño3指数集合平均预报与“真值”的相关系数。图中虚线是各模式的相关系数通过置信水平为95%的显著性检验的临界值 Figure 11 Correlation coefficients between the predicted Niño3 index for EP-El Niño events and that of true events. The predicted Niño3 index is obtained by conducting ensemble-mean forecast with assimilation of observed SST in PP_max_R (yellow lines), PP_max (red lines) regions, and three randomly selected regions (blue, green, and pink lines) respectively using the selected models listed in Table 1. The dashed lines denote significance correlation at the 95% confidence level |
KD提出的粒子滤波—目标观测方法利用集合样本离散度度量初值敏感性,但该敏感性不能保证等同于集合平均预报误差度量的初值敏感性,从而使得KD目标观测敏感区的有效性往往在预报试验中得不到验证。针对KD方法的这种局限性,该研究依据集合预报系统的可靠性条件——集合样本离散度和集合平均预报误差呈正相关关系,提出了新的粒子滤波—目标观测方法,即在应用KD方法之前,首先计算集合样本离散度和集合平均预报误差呈现较强正相关关系的区域,然后在该区域考察PP指数的大值区,将该大值区作为目标观测敏感区。
将新的粒子滤波—目标观测方法应用于揭示两类El Niño的目标观测敏感区,并与KD方法进行了对比。结果表明,对于CP-El Niño事件,KD方法确定的目标观测敏感区为赤道中太平洋,而新方法确定的敏感区除了包含赤道中太平洋区域外,还强调了赤道东太平洋区域,而且通过粒子滤波同化试验表明,同化新敏感区的目标观测,不仅成功预报出CP-El Niño的发生,而且较同化旧敏感区的观测大大减小了集合预报样本的离散度和集合平均预报误差,显著提高了CP-El Niño的预报技巧。对于EP-El Niño事件,KD方法和新方法确定的敏感区都位于赤道东太平洋,但后者比前者要明显东移,位于150°~120°W以东,而且同化后者的目标观测进行集合预报,与同化其他区域的观测相比,无论是集合平均预报误差,还是Niño3指数演变的相关系数都获得更高的预报技巧。所以,新方法识别的敏感区更适合作为EP-El Niño和CP-El Niño事件的目标观测敏感区,可为新的热带太平洋观测计划(如Tropical Pacific Observing System 2020, Cravatte et al., 2016)提供可供参考的优化观测方案。
利用新方法确定的两类El Niño事件的目标观测敏感区都强调了赤道东太平洋海温观测的重要性,即是说两类El Niño的预测都对赤道东太平洋的初始海温误差比较敏感。Mu et al.(2014)表明,热带太平洋的海温初始误差的发展与信号El Niño的发展机理类似,即是说,热带太平洋的海温初始误差要么演变为一个类EP-El Niño,要么为一个类CP-El Niño,要么为一个类La Nina事件。在确定目标观测敏感区时,从误差增长的角度我们寻找的是能够导致最大预报误差的最快增长初始误差,对比热带太平洋初始误差发展的模态,类EP-El Niño事件一般强于类CP-El Niño和La Nina事件(这在观测中也是成立的),即是说发展为类EP-El Niño事件的预报误差最大,其对应的初始误差模态是最快增长初始误差,而该类初始误差往往位于赤道东太平洋。因此,赤道东太平洋为两类El Niño事件的目标观测敏感区之一,从而解释了为什么两类El Niño事件的目标观测敏感区均强调了赤道东太平洋区域。
上述结论是通过将模式中的El Niño事件作为真值进行预报预测得到的,下一步的工作应是将观测的El Niño事件作为预报对象,用粒子滤波方法确定目标观测敏感区,从而验证上述结论。用观测的El Niño确定目标观测敏感区,应是更为实际的做法,但考虑到该研究使用了多模式的结果,而且选取了模式积分中所有的El Niño事件作为研究对象,所得结果对实际预报预测应具有指示意义。我们注意到,上述目标观测敏感区具有一定的模式依赖性,毫无疑问这是由模式之间的偏差导致的。事实上,敏感区的确定,应考虑在多模式PP指数空间分布的集合平均且通过显著性检验的区域基础之上进行。但本文中能够模拟两类El Niño事件的模式相对较少,无法考虑统计集合平均的结果,期望未来能够使用更多的模式得到更可靠的两类El Niño事件的目标观测敏感区。另外,该研究使用CMIP5模式的PI-control试验资料,不考虑外强迫随时间变化的情况,因而可以认为不同El Niño年之间的偏差仅由它们的初始偏差所导致,不受模式误差的影响,从而可以将粒子滤波同化方法应用于上述模式资料,考察初值敏感性对预报结果的影响。事实上,在粒子滤波同化的应用中,我们也可以考虑随时间变化的外强迫影响下的模式资料。该情形下,对于资料同化,我们考虑的问题即为在时变外强迫的影响下(如CO2增暖情形下),同化初值在多大程度上可以提高El Niño的预报技巧。该问题是更接近实际世界的科学问题,值得未来的研究深入探讨。粒子滤波针对模式资料选取集合样本,同化观测赋予集合样本不同权重,而进行集合预报。该思路也可以应用于实际,对关心的异常事件进行预报预测,而且由于该思路所涉及的预报预测只利用已有的模式资料,从而可以大大节省计算时间,是一个可选择的有效的预报预测方法。
Alexander M A, Bladé I, Newman M, et al. 2002. The atmospheric bridge:The influence of ENSO teleconnections on air-sea interaction over the global oceans [J]. J. Climate, 15(16): 2205-2231. DOI:10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO;2
|
Baker N L, Daley R. 2000. Observation and background adjoint sensitivity in the adaptive observation-targeting problem [J]. Quart. J. Roy. Meteor. Soc., 126(565): 1431-1454. DOI:10.1002/qj.49712656511
|
Bishop C H, Toth Z. 1999. Ensemble transformation and adaptive observations [J]. J. Atmos. Sci., 56(11): 1748-1765. DOI:10.1175/1520-0469(1999)056<748:ETAAO>2.0.CO;2
|
Bishop C H, Etherton B J, Majumdar S J. 2001. Adaptive sampling with the ensemble transform Kalman filter [M]. Part Ⅰ: Theoretical aspects[J]. Mon. Wea. Rev.: 420-436. DOI:10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2
|
Bjerknes J. 1969. Atmospheric teleconnections from the equatorial Pacific [J]. Mon. Wea. Rev., 97(3): 163-172. DOI:10.1175/1520-0493(1969)097<0163:ATFTEP>2.3.CO;2
|
Branković Č, Molteni F, Palmer T N, et al. 1988. Extended range ensemble forecasting at ECMWF[C]//Proceedings of ECMWF Workshop on Predictability in the Medium and Extended Range. Shinfield Park, Reading: ECMWF. http://bib.irb.hr/prikazi-rad?rad=493080
|
Cane M A. 1983. Oceanographic events during El Niño [J]. Science, 222(4629): 1189-1195. DOI:10.1126/science.222.4629.1189
|
Chen D, Cane M A. 2008. El Niño prediction and predictability [J]. J. Comput. Phys., 227(7): 3625-3640. DOI:10.1016/j.jcp.2007.05.014
|
Chen D, Cane M A, Kaplan A, et al. 2004. Predictability of El Niño over the past 148 years [J]. Nature, 428(6984): 733-736. DOI:10.1038/nature02439
|
丑纪范, 郜吉东. 1995. 长期数值天气预报(修订版)[M]. 北京: 气象出版社. Chou J F, Gao J D. 1995. Long-Term Numerical Weather Prediction (in Chinese)[M]. Beijing: China Meteorological Press.
|
Cravatte S, Kessler W S, Smith N, et al. 2016. First Report of TPOS 2020[R]. GOOS-215, 200pp.
|
Duan W S, Mu M. 2009. Conditional nonlinear optimal perturbation:Applications to stability, sensitivity, and predictability [J]. Sci. China Ser. D:Earth Sci., 52(7): 883-906. DOI:10.1007/s11430-009-0090-3
|
Duan W S, Wei C. 2013. The 'spring predictability barrier' for ENSO predictions and its possible mechanism:Results from a fully coupled model [J]. Int. J. Climatol., 33(5): 1280-1292. DOI:10.1002/joc.3513
|
Duan W S, Hu J Y. 2016. The initial errors that induce a significant "spring predictability barrier" for El Niño events and their implications for target observation:Results from an earth system model [J]. Climate Dyn., 46(11-12): 3599-3615. DOI:10.1007/s00382-015-2789-5
|
Duan W S, Liu X C, Zhu K Y, et al. 2009. Exploring the initial errors that cause a significant "spring predictability barrier" for El Niño events [J]. J. Geophys. Res., 114(C4): C04022. DOI:10.1029/2008JC004925
|
Feng J, Chen W, Tam C Y, et al. 2011. Different impacts of El Niño and El Niño Modoki on China rainfall in the decaying phases [J]. Int. J. Climatol., 31(14): 2091-2101. DOI:10.1002/joc.2217
|
Fischer M, Latif M, Flügel M, et al. 1997. The impact of data assimilation on ENSO simulations and predictions [J]. Mon. Wea. Rev., 125(5): 819-830. DOI:10.1175/1520-0493(1997)125<0819:TIODAO>2.0.CO;2
|
Ham Y G, Sung M K, An S I, et al. 2014. Role of tropical Atlantic SST variability as a modulator of El Niño teleconnections [J]. Asia Pac. J. Atmos. Sci., 50(3): 247-261. DOI:10.1007/s13143-014-0013-x
|
Hamill T M, Snyder C. 2002. Using improved background-error covariances from an ensemble Kalman filter for adaptive observations [J]. Mon. Wea. Rev., 130(6): 1552-1572. DOI:10.1175/1520-0493(2002)130<1552:UIBECF>2.0.CO;2
|
Hendon H H, Lim E, Wang G M, et al. 2009. Prospects for predicting two flavors of El Niño [J]. Geophys. Res. Lett., 36(19): L19713. DOI:10.1029/2009GL040100
|
Hoerling M P, Kumar A, Zhong M. 1997. El Niño, La Niña, and the nonlinearity of their teleconnections [J]. J. Climate, 10(8): 1769-1786. DOI:10.1175/1520-0442(1997)010<1769:ENOLNA>2.0.CO;2
|
Hu J Y, Duan W S. 2016. Relationship between optimal precursory disturbances and optimally growing initial errors associated with ENSO events:Implications to target observations for ENSO prediction [J]. J. Geophys. Res., 121(5): 2901-2917. DOI:10.1002/2015JC011386
|
Hu Z Z, Kumar A, Jha B, et al. 2012. An analysis of warm pool and cold tongue El Niños:Air-sea coupling processes, global influences, and recent trends [J]. Climate Dyn., 38(9-10): 2017-2035. DOI:10.1007/s00382-011-1224-9
|
Jeong H I, Lee D Y, Ashok K, et al. 2012. Assessment of the APCC coupled MME suite in predicting the distinctive climate impacts of two flavors of ENSO during boreal winter [J]. Climate Dyn., 39(1-2): 475-493. DOI:10.1007/s00382-012-1359-3
|
Jin E K, Kinter III J L, Wang B, et al. 2008. Current status of ENSO prediction skill in coupled ocean-atmosphere models [J]. Climate Dyn., 31(6): 647-664. DOI:10.1007/s00382-008-0397-3
|
Kalnay E. 2002. Atmospheric Modeling, Data Assimilation and Predictability [M]. Cambridge University Press.
|
Kao H Y, Yu J Y. 2009. Contrasting eastern Pacific and central Pacific types of ENSO [J]. J. Climate, 22(3): 615-632. DOI:10.1175/2008JCLI2309.1
|
Kirtman B P, Shukla J, Balmaseda M, et al. 2001. Current status of ENSO forecast skill: A report to the CLIVAR working group on seasonal to interannual prediction[R]. ICPO Publication No. 56. https://www.researchgate.net/publication/313097026_Current_status_of_ENSO_forecast_skill_a_report_to_the_CLIVAR_Working_Group_on_Seasonal_to_Interannual_Prediction
|
Kramer K, Dijkstra H A. 2013. Optimal localized observations for advancing beyond the ENSO predictability barrier [J]. Nonlinear Process. Geophys., 20(2): 221-300. DOI:10.5194/npg-20-221-2013
|
Kug J S, Jin F F, An S I. 2009. Two types of El Niño events:Cold tongue El Niño and warm pool El Niño [J]. J. Climate, 22(6): 1499-1515. DOI:10.1175/2008JCLI2624.1
|
Kug J S, Choi J, An S I, et al. 2010. Warm pool and cold tongue El Niño events as simulated by the GFDL 2.1 coupled GCM [J]. J. Climate, 23(5): 1226. DOI:10.1175/2009JCLI3293.1
|
Langland R H, Rohaly G D. 1996. Adjoint-based targeting of observations for FASTEX cyclones[R]. Monterey, CA: Naval Research Lab. https://www.researchgate.net/publication/228788695_Adjoint-based_targeting_of_observations_for_FASTEX_cyclones
|
Langland R H, Toth Z, Gelaro R, et al. 1999. The North Pacific experiment (NORPEX-98):Targeted observations for improved North American weather forecasts [J]. Bull. Amer. Meteor. Soc., 80(7): 1363-1384. DOI:10.1175/1520-0477(1999)080<1363:TNPENT>2.0.CO;2
|
Lorenz E N. 1963. Deterministic nonperiodic flow [J]. J. Atmos. Sci., 20(2): 130-141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
|
Lorenz E N, Emanuel K A. 1998. Optimal sites for supplementary weather observations:Simulation with a small model [J]. J. Atmos. Sci., 55(3): 399-414. DOI:10.1175/1520-0469(1998)055<0399:OSFSWO>2.0.CO;2
|
Luo J J, Masson S, Behera S, et al. 2003. South Pacific origin of the decadal ENSO-like variation as simulated by a coupled GCM [J]. Geophys. Res. Lett., 30(24): 2250. DOI:10.1029/2003GL018649
|
Luo J J, Masson S, Roeckner E, et al. 2005. Reducing climatology bias in an ocean-atmosphere CGCM with improved coupling physics [J]. J. Climate, 18(13): 2344-2360. DOI:10.1175/JCLI3404.1
|
Luo J J, Masson S, Behera S K, et al. 2008. Extended ENSO predictions using a fully coupled ocean-atmosphere model [J]. J Climate, 21(1): 84-93. DOI:10.1175/2007JCLI1412.1
|
McPhaden M J, Zebiak S E, Glantz M H. 2006. ENSO as an integrating concept in Earth science [J]. Science, 314(5806): 1740-1745. DOI:10.1126/science.1132588
|
Moore A M, Kleeman R. 1996. The dynamics of error growth and predictability in a coupled model of ENSO [J]. Quart. J. Roy. Meteor. Soc., 122(534): 1405-1446. DOI:10.1002/qj.49712253409
|
Morss R E, Emanuel K A, Snyder C. 2001. Idealized adaptive observation strategies for improving numerical weather prediction [J]. J. Atmos. Sci., 58(2): 210-232. DOI:10.1175/1520-0469(2001)058<0210:IAOSFI>2.0.CO;2
|
Mu M. 2013. Methods, current status, and prospect of targeted observation [J]. Sci. China Earth Sci., 56(12): 1997-2005. DOI:10.1007/s11430-013-4727-x
|
Mu M, Duan W S, Wang B. 2003. Conditional nonlinear optimal perturbation and its applications [J]. Nonlinear Process. Geophys., 10(6): 493-501. DOI:10.5194/npg-10-493-2003
|
Mu M, Duan W S, Wang B. 2007a. Season-dependent dynamics of nonlinear optimal error growth and El Niño-southern oscillation predictability in a theoretical model [J]. J. Geophys. Res., 112(D10): D10113. DOI:10.1029/2005JD006981
|
Mu M, Xu H, Duan W S. 2007b. A kind of initial errors related to "spring predictability barrier" for El Niño events in Zebiak-Cane model [J]. Geophys. Res. Lett., 34(3): L03709. DOI:10.1029/2006GL027412
|
Mu M, Yu Y S, Xu H, et al. 2014. Similarities between optimal precursors for ENSO events and optimally growing initial errors in El Niño predictions [J]. Theor. Appl. Climatol., 115(3-4): 461-469. DOI:10.1007/s00704-013-0909-x
|
Palmer T N, Gelaro R, Barkmeijer J, et al. 1998. Singular vectors, metrics, and adaptive observations [J]. J. Atmos. Sci., 55(4): 633-653. DOI:10.1175/1520-0469(1998)055<0633:SVMAAO>2.0.CO;2
|
Philander S G H. 1983. El Niño Southern Oscillation phenomena [J]. Nature, 302(5906): 295-301. DOI:10.1038/302295a0
|
Qi Q Q, Duan W S, Zheng F, et al. 2017. On the "spring predictability barrier" for strong El Niño events as derived from an intermediate coupled model ensemble prediction system [J]. Sci. China Earth Sci., 60(9): 1614-1631. DOI:10.1007/s11430-017-9087-2
|
Rasmusson E M, Wallace J M. 1983. Meteorological aspects of the El Niño/Southern Oscillation [J]. Science, 222(4629): 1195-1202. DOI:10.1126/science.222.4629.1195
|
Riehl H, Haggard W H, Sanborn R W. 1956. On the prediction of 24-hour hurricane motion [J]. J. Meteor., 13(5): 415-420. DOI:10.1175/1520-0469(1956)013<0415:OTPOHH>2.0.CO;2
|
Ropelewski C F, Halpert M S. 1987. Global and regional scale precipitation patterns associated with the El Niño/Southern Oscillation [J]. Mon. Wea. Rev., 115(8): 1606-1626. DOI:10.1175/1520-0493(1987)115<1606:GARSPP>2.0.CO;2
|
Schneider T, Griffies S M. 1999. A conceptual framework for predictability studies [J]. J. Climate, 12(10): 3133-3155. DOI:10.1175/1520-0442(1999)012<3133:ACFFPS>2.0.CO;2
|
Snyder C. 1996. Summary of an informal workshop on adaptive observations and FASTEX [J]. Bull. Amer. Meteor. Soc., 77: 953-961. DOI:10.1175/1520-0477-77.5.953
|
Taschetto A S, England M H. 2009. El Niño Modoki impacts on Australian rainfall [J]. J. Climate, 22(11): 3167-3174. DOI:10.1175/2008JCLI2589.1
|
Tian B, Duan W S. 2016. Comparison of the initial errors most likely to cause a spring predictability barrier for two types of El Niño events [J]. Climate Dyn., 47(3-4): 779-792. DOI:10.1007/s00382-015-2870-0
|
Toth Z, Kalnay E. 1997. Ensemble forecasting at NCEP and the breeding method [J]. Mon. Wea. Rev., 125(12): 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2
|
Trenberth K E, Branstator G W, Karoly D, et al. 1998. Progress during TOGA in understanding and modeling global teleconnections associated with tropical sea surface temperatures [J]. J. Geophys. Res., 103(C7): 14291-14324. DOI:10.1029/97JC01444
|
Van Leeuwen P J. 2009. Particle filtering in geophysical systems [J]. Mon. Wea. Rev., 137(12): 4089-4114. DOI:10.1175/2009MWR2835.1
|
Wang C Z, Picaut J. 2004. Understanding ENSO physics-A review[M]//Wang C, Xie S P, Carton J A. Earth's Climate: The Ocean-Atmosphere Interaction. Washington, DC: AGU, doi: 10.1029/147GM02.
|
Wang C Z, Fiedler P C. 2006. ENSO variability and the eastern tropical Pacific:A review [J]. Prog. Oceanogr., 69(2-4): 239-266. DOI:10.1016/j.pocean.2006.03.004
|
Wang C Z, Wang X. 2013. Classifying El Niño Modoki Ⅰ and Ⅱ by different impacts on rainfall in southern China and typhoon tracks [J]. J. Climate, 26(4): 1322-1338. DOI:10.1175/JCLI-D-12-00107.1
|
Weng H Y, Ashok K, Behera S K, et al. 2007. Impacts of recent El Niño Modoki on dry/wet conditions in the Pacific rim during boreal summer [J]. Climate Dyn., 29(2-3): 113-129. DOI:10.1007/s00382-007-0234-0
|
Wu C C, Chen J H, Lin P H, et al. 2007. Targeted observations of tropical cyclone movement based on the adjoint-derived sensitivity steering vector [J]. J. Atmos. Sci., 64(7): 2611-2626. DOI:10.1175/JAS3974.1
|
Xiang B Q, Wang B, Li T. 2013. A new paradigm for the predominance of standing central Pacific warming after the late 1990s [J]. Climate Dyn., 41(2): 327-340. DOI:10.1007/s00382-012-1427-8
|
Xue Y, Chen M Y, Kumar A, et al. 2013. Prediction skill and bias of tropical Pacific sea surface temperatures in the NCEP climate forecast system version2 [J]. J. Climate, 26(15): 5358-5378. DOI:10.1175/JCLI-D-12-00600.1
|
Yu Y S, Duan W S, Xu H, et al. 2009. Dynamics of nonlinear error growth and season-dependent predictability of El Niño events in the Zebiak-Cane model [J]. Quart. J. Roy. Meteor. Soc., 135(645): 2146-2160. DOI:10.1002/qj.526
|
Zebiak S E, Cane M A. 1987. A model El Niño-southern oscillation [J]. Mon. Wea. Rev., 115(10): 2262-2278. DOI:10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2
|
Zhang W J, Jin F F, Li J P, et al. 2011. Contrasting impacts of two-type El Niño over the western North Pacific during boreal autumn [J]. J. Meteor. Soc. Japan, 89(5): 563-569. DOI:10.2151/jmsj.2011-510
|
Zhang J, Duan W S, Zhi X F. 2015. Using CMIP5 model outputs to investigate the initial errors that cause the "spring predictability barrier" for El Niño events [J]. Sci. China Earth Sci., 58(5): 685-696. DOI:10.1007/s11430-014-4994-1
|
 2018, Vol. 42
2018, Vol. 42


