1 引言

海洋环流模式不仅是物理海洋研究的基本工具，也是地球系统模式的重要分量之一，已经广泛地应用于海—气相互作用、短期气候异常预测和气候变化预估等诸多方面的研究，因此海洋环流模式研发和应用受到了各国学者的广泛重视。自20世纪60年代开始，国际上就开始了基于原始方程的海洋环流模式的研制和应用研究，目前比较流行的海洋环流模式包括美国地球流体实验室研制的Modular Ocean Model（简称MOM；Griffies, 2009）、美国佛罗里达大学研制的Hybrid Coordinate Ocean Model（简称HYCOM；Chassignet et al., 2003）、法国学者研制的Nucleus for European Modelling of the Ocean（简称NEMO；Madec, 2008）等。由于海洋环流模式在海洋和大气科学研究领域的重要性，自从上世纪八十年代末以来，中国科学院大气物理研究所（IAP）大气科学和地球流体力学数值模拟国家重点实验室（LASG）的科学家一直致力于自主发展全球海洋环流模式。张学洪等发展了我国第一个全球海洋环流模式（Zhang and Liang, 1989），水平分辨率为4°×5°，垂直方向分为四层。以此为基础，LASG的科学家不断改进模式的物理参数化过程和提高空间分辨率，至今已经成功发展了四代全球海洋环流模式（Zhang et al., 1996; Jin et al., 1999; Liu et al., 2004, 2012）。其中第四代全球海洋环流模式，即LASG气候系统海洋模式（LASG/IAP Climate system Ocean Model，简称LICOM），目前已经发展了两个版本（LICOM1.0和改进后的LICOM2.0），这两个版本标准的水平分辨率都是1°，分别作为海洋分量模式已经用于LASG耦合模式FGOALS的不同版本。随着近年来国家对科研投入不断增加，我国在大气和海洋科学领域的高性能计算能力也已接近美国、日本等发达国家，这为我国自主发展全球涡分辨率的海洋环流模式奠定了硬件基础。大气物理研究所的科学家最近在LICOM2.0的基础上，把模式水平分辨率提高到全球均匀的(1/10)°，垂直分辨率提高到55层，并对模式的动力框架和并行方案进行必要改动之后，建立了一个准全球（模式区域为78°S~66°N，不包含北冰洋）涡分辨率海洋环流模式（俞永强等，2012）。同国际上其他涡分辨率模式类似，该模式可以重现许多中尺度涡旋的特征，特别是在黑潮及其延伸体、湾流及其延伸体以及南大洋绕极环流区域，海洋中尺度涡旋显得非常活跃，同时模式模拟的西边界流也更为合理。

虽然上述高分辨率的LICOM模式在很多方面都表现出优异的性能，但是由于采用经纬网格，为了避免纬向格距随纬度增加急剧减小带来的计算稳定性以及北极点的奇异性问题，其北边界为66°N，无法刻画北冰洋的环流特征。即使对于100 km低分辨率的LICOM模式经纬网格版本，北极点附近仍然作为一个孤岛处理，对北极海洋环流和海冰的模拟均有不利的影响。为了解决经纬网格在北极点附近的奇异性，一般在保证网格正交性的前提下采用坐标变化的方法将北极点旋转到陆地上。通常有两种方案，第一是采用两极坐标，南极点保持原有位置不变，而北极点旋转到北美大陆或者欧亚大陆；第二是采用三极网格，南极点仍然保持原有位置不变，而北极点则一分为二，分别安放在北美大陆和欧亚大陆上（Murray, 1996）。第一种方案会导致全球范围内的网格变形，生成的正交坐标曲线与经纬网格完全不重合；第二种方案生成的正交曲线坐标，除了北半球高纬度之外，在全球大部分区域所得到的正交曲线网格与经纬网格均十分接近。旋转的两极网格最早应用于GFDL（Geophysical Fluid Dynamics Laboratory）的MOM海洋模式，随后也应用于其他主流的海洋环流模式，但是近年来世界上大部分海洋模式都采取第二种方案，即三极网格坐标。对于一个海洋模式来说，无论是采用旋转两极网格还是三极网格，都必须重新改写模式的动力框架，即将原来基于经纬网格坐标的原始方程组及其离散化数值算法重新改写，使之适用于任意的正交曲线坐标系。

本文的主要目的，就是改进IAP研制的海洋模式LICOM2.0的动力框架，将原来基于经纬网格坐标的动力框架进行重新改写，使之可以适用于任意的水平正交曲线坐标系，其中第2节主要描述在任意正交曲线坐标系下的模式原始方程组及其差分算法，第3节则描述了动力框架在其他方面的改进，第4节通过数值试验评估了改进的海洋模式动力框架，第5节是总结，其后的附录则给出了三极网格在北极点附近的处理方案和任意正交曲线坐标系下的平流计算方案以及三极网格下经向翻转流函数和热输送的计算方案。

2 任意正交曲线坐标系下的模式原始方程和差分格式 2.1 任意正交曲线坐标下的模式原始方程组

在球坐标下，LICOM2.0采用如下原始方程组（刘海龙等，2004）：

$ \left\{ \begin{align} & \frac{\partial v}{\partial t}+L\left( v \right)=-\frac{1}{{{\rho }_{0}}}\frac{\partial p}{a\partial \theta }-{{f}^{\text{*}}}u+{{F}_{\text{m}x}}+\frac{\partial }{\partial z}\left( {{K}_{\text{m}}}\frac{\partial v}{\partial z} \right), \\ & \frac{\partial u}{\partial t}+L\left( u \right)=-\frac{1}{{{\rho }_{0}}}\frac{\partial p}{a\text{sin}\theta \partial \lambda }+{{f}^{\text{*}}}v+{{F}_{\text{m}y}}+\frac{\partial }{\partial z}\left( {{K}_{\text{m}}}\frac{\partial u}{\partial z} \right), \\ & \frac{\partial p}{\partial z}=-\rho g, \\ & \frac{1}{a\text{sin}\theta }(\frac{\partial v\text{sin}\theta }{\partial \theta }+\frac{\partial u}{\partial \lambda })+\frac{\partial w}{\partial z}=0, \\ & \frac{\partial T}{\partial t}+L\left( T \right)={{A}_{T}}{{\nabla }^{2}}T+\frac{\partial }{\partial z}\left( {{K}_{T}}\frac{\partial T}{\partial z} \right)+{{C}_{T}}+{{Q}_{\text{pen}}}, \\ & \frac{\partial S}{\partial t}+L\left( S \right)={{A}_{S}}{{\nabla }^{2}}S+\frac{\partial }{\partial z}\left( {{K}_{S}}\frac{\partial S}{\partial z} \right)+{{C}_{S}}, \\ & \rho =\rho \left( T,S,p \right), \\ \end{align} \right. $

(1)

其中，$u, v, w$是$\lambda $、$\theta $和z三个方向的运动速度，$\theta $是余纬，$\lambda $是经度，T和S分别是温度和盐度，$\rho $是现场密度，p是压力，f^*是Coriolis参数，Q_pen为短波辐射穿透项，K_m为速度的垂直湍流粘性系数，K_T和K_S为温度和盐度的垂直湍流扩散系数，A_T和A_S为温度和盐度的水平湍流扩散系数，C_T和C_S为垂直对流项，F_mx和F_my为水平湍流粘性项，

$ \left\{ {\begin{array}{*{20}{c}} {{F_{{\rm{m}}x}} = {A_{\rm{m}}}\left({{\nabla ^2}v + \frac{{1 - {{\cot }^2}\theta }}{{{a^2}}}v - \frac{{2{\rm{cos}}\theta }}{{{a^2}{\rm{si}}{{\rm{n}}^2}\theta }}\frac{{\partial u}}{{\partial \lambda }}} \right), } \\ {{F_{{\rm{m}}y}} = {A_{\rm{m}}}\left({{\nabla ^2}u + \frac{{1 - {{\cot }^2}\theta }}{{{a^2}}}u + \frac{{2{\rm{cos}}\theta }}{{{a^2}{\rm{si}}{{\rm{n}}^2}\theta }}\frac{{\partial v}}{{\partial \lambda }}} \right), } \end{array}} \right. $

(2)

其中，${\nabla ^2}$为水平Laplace算子，A_m水平湍流粘性系数，$\mathcal{L}$是平流算子，表达式为

$ \left\{ \begin{align} &{{\nabla }^{2}}=\frac{1}{{{a}^{2}}\text{si}{{\text{n}}^{2}}\theta }~\frac{{{\partial }^{2}}}{\partial {{\lambda }^{2}}}~+\frac{1}{{{a}^{2}}\text{si}{{\text{n}}^{2}}\theta }~\frac{\partial }{\partial \theta }\left(\text{sin}\theta \frac{\partial }{\partial \theta } \right), \\ &L=v\frac{\partial }{a\partial \theta }+u\frac{\partial }{a\text{sin}\theta \partial \lambda }+w\frac{\partial }{\partial z}. \\ \end{align} \right. $

(3)

为得到在任意正交曲线坐标系下的模式方程组，考虑从一个局地直角坐标系下或者更确切地说是三维欧式空间（x₁，x₂，x₃）到另外一组任意正交曲线坐标系（${\xi _1}, {\rm{ }}{\xi _2}, {\rm{ }}{\xi _3}$）的坐标变换，假设两个坐标系之间存在如下映射关系：

$ \left\{ {\begin{array}{*{20}{c}} {{x_1} = {x_1}({\xi _1}, {\rm{ }}{\xi _2}, {\rm{ }}{\xi _3}), } \\ {{x_2} = {x_2}({\xi _1}, {\rm{ }}{\xi _2}, {\rm{ }}{\xi _3}), } \\ {{x_3} = {x_3}({\xi _1}, {\rm{ }}{\xi _2}, {\rm{ }}{\xi _3}), } \end{array}} \right. $

(4)

根据链式求导法则：

$ \left\{ {\begin{array}{*{20}{c}} {{\rm{d}}{x_1} = \left({\frac{{\partial {x_1}}}{{\partial {\xi _1}}}} \right){\rm{d}}{\xi _1} + \left({\frac{{\partial {x_1}}}{{\partial {\xi _2}}}} \right){\rm{d}}{\xi _2} + \left({\frac{{\partial {x_1}}}{{\partial {\xi _3}}}} \right){\rm{d}}{\xi _3}, } \\ {{\rm{d}}{x_2} = \left({\frac{{\partial {x_2}}}{{\partial {\xi _1}}}} \right){\rm{d}}{\xi _1} + \left({\frac{{\partial {x_2}}}{{\partial {\xi _2}}}} \right){\rm{d}}{\xi _2} + \left({\frac{{\partial {x_2}}}{{\partial {\xi _3}}}} \right){\rm{d}}{\xi _3}, } \\ {{\rm{d}}{x_3} = \left({\frac{{\partial {x_3}}}{{\partial {\xi _1}}}} \right){\rm{d}}{\xi _1} + \left({\frac{{\partial {x_3}}}{{\partial {\xi _2}}}} \right){\rm{d}}{\xi _2} + \left({\frac{{\partial {x_3}}}{{\partial {\xi _3}}}} \right){\rm{d}}{\xi _3}, } \end{array}} \right. $

(5)

在欧式空间里，无限小线段元的长度ds可表示为

${\rm{d}}{s^2} = {\rm{d}}{x_1}^2 + {\rm{d}}{x_2}^2 + {\rm{d}}{x_3}^2, $

(6)

将其代入公式（5）中可以得到：

$ {\rm{d}}{s^2} = {g_{ij}}{\rm{d}}{\xi _i}{\rm{d}}{\xi _j} $

(7)

其中，${g_{ij}} \equiv \frac{{\partial {x_k}}}{{\partial {\xi _i}}}\frac{{\partial {x_k}}}{{\partial {\xi _j}}}$是正交曲线坐标系的度量张量。此处利用了爱因斯坦张量求和约定，即对重复指标进行求和。当两个坐标系都为正交坐标系时，很容易证明度量张量${g_{ij}}$为一正定对角矩阵，即满足如下条件：

$ \left\{ {\begin{array}{*{20}{c}} {{g_{ij}} = 0, i \ne j, } \\ {{g_{ii}} > 0, i = j, } \end{array}} \right. $

(8)

因此可以令${h_i}^2 = {g_{ii}}$，h_i就是所谓的拉梅系数，代入公式（7）则有

$ {\rm{d}}{s^2} = {h_1}^2{\rm{d}}{\xi _1}^2 + {h_2}^2{\rm{d}}{\xi _2}^2 + {h_3}^2{\rm{d}}{\xi _3}^2 $

(9)

由公式（9）可以看出，拉梅系数的物理含义就是在正交曲线坐标系下单位长度的基矢量在直角坐标系也就是物理空间中真实的长度，因此拉梅系数又被称为地图放大因子。如果坐标系（${\xi _1}, {\xi _2}, {\xi _3}$）是在球面上的正交曲线坐标系，则有

$ \left\{ \begin{gathered} {h_1}^2 = {(\frac{{\partial {x_1}}}{{\partial {\xi _1}}})^2} + {(\frac{{\partial {x_2}}}{{\partial {\xi _1}}})^2} + {(\frac{{\partial {x_3}}}{{\partial {\xi _1}}})^2}, \hfill \\ {h_2}^2 = {(\frac{{\partial {x_1}}}{{\partial {\xi _2}}})^2} + {(\frac{{\partial {x_2}}}{{\partial {\xi _2}}})^2} + {(\frac{{\partial {x_3}}}{{\partial {\xi _2}}})^2}, \hfill \\ {h_3}^2 = {(\frac{{\partial {x_1}}}{{\partial {\xi _3}}})^2} + {(\frac{{\partial {x_2}}}{{\partial {\xi _3}}})^2} + {(\frac{{\partial {x_3}}}{{\partial {\xi _3}}})^2}, \hfill \\ \end{gathered} \right. $

(10)

如果仅仅考虑球面上水平网格的坐标系变化，垂直坐标系不变，则有h₃=1。由此在任意正交曲线坐标系下的模式原始方程为

$ \left\{ \begin{align} & \frac{\partial {{u}_{x}}}{\partial t}+L\left( {{u}_{x}} \right)=-\frac{1}{{{\rho }_{0}}}\frac{\partial p}{{{h}_{1}}\partial {{\xi }_{1}}}-{{f}^{\text{*}}}{{u}_{y}}+{{F}_{\text{m}x}}+\frac{\partial }{\partial {{\xi }_{3}}}\left( {{K}_{\text{m}}}\frac{\partial {{u}_{x}}}{\partial {{\xi }_{3}}} \right), \\ & \frac{\partial {{u}_{y}}}{\partial t}+L\left( {{u}_{y}} \right)=-\frac{1}{{{\rho }_{0}}}\frac{\partial p}{{{h}_{2}}\partial {{\xi }_{2}}}+{{f}^{\text{*}}}{{u}_{x}}+{{F}_{\text{m}y}}+\frac{\partial }{\partial {{\xi }_{3}}}\left( {{K}_{\text{m}}}\frac{\partial {{u}_{y}}}{\partial {{\xi }_{3}}} \right), \\ & \frac{\partial p}{\partial z}=-\rho g, \\ & \frac{1}{{{h}_{1}}{{h}_{2}}}\left( \frac{\partial {{h}_{2}}{{u}_{x}}}{\partial {{\xi }_{1}}}+\frac{\partial {{h}_{1}}{{u}_{y}}}{\partial {{\xi }_{2}}} \right)+\frac{\partial w}{\partial {{\xi }_{3}}}=0, \\ & \frac{\partial T}{\partial t}+L\left( T \right)={{A}_{T}}{{\nabla }^{2}}T+\frac{\partial }{\partial {{\xi }_{3}}}\left( {{K}_{T}}\frac{\partial T}{\partial {{\xi }_{3}}} \right)+{{C}_{T}}+{{Q}_{\text{pen}}}, \\ & \frac{\partial S}{\partial t}+L\left( S \right)={{A}_{S}}{{\nabla }^{2}}S+\frac{\partial }{\partial {{\xi }_{3}}}\left( {{K}_{S}}\frac{\partial T}{\partial {{\xi }_{3}}} \right)+{{C}_{S}}, \\ & \rho =\rho \left( T,S,p \right), \\ \end{align} \right. $

(11)

其中，u_x、u_y为沿球面正交曲线基矢量方向的水平速度，动量方程中的水平粘性项可以写作（Griffies, 2009）：

$ {F_{{\rm{m}}x}} = {A_{\rm{m}}}\left({{\nabla ^2}{u_x} - {u_x}\left({\frac{{\partial {K_x}}}{{{h_1}\partial {\xi _1}}} + \frac{{\partial {K_y}}}{{{h_2}\partial {\xi _2}}} + 2{K_x}^2 + 2{K_y}^2} \right) + } \right. \\ \left. {{u_y}\left({\frac{{\partial {K_x}}}{{{h_2}\partial {\xi _2}}} - \frac{{\partial {K_y}}}{{{h_1}\partial {\xi _1}}}} \right) + 2{K_y}\left({\frac{{\partial {u_y}}}{{{h_1}\partial {\xi _1}}}} \right) - 2{K_x}\left({\frac{{\partial {u_y}}}{{{h_2}\partial {\xi _2}}}} \right)} \right), $

(12)

$ {F_{{\rm{m}}y}} = {A_{\rm{m}}}\left({{\nabla ^2}{u_y} - {u_y}\left({\frac{{\partial {K_x}}}{{{h_1}\partial {\xi _1}}} + \frac{{\partial {K_y}}}{{{h_2}\partial {\xi _2}}} + 2{K_x}^2 + 2{K_y}^2} \right) + } \right.\\ \left. {{u_x}\left({\frac{{\partial {K_y}}}{{{h_1}\partial {\xi _1}}} - \frac{{\partial {K_x}}}{{{h_2}\partial {\xi _2}}}} \right) + 2{K_x}\left({\frac{{\partial {u_x}}}{{{h_2}\partial {\xi _2}}}} \right) - 2{K_y}\left({\frac{{\partial {u_x}}}{{{h_1}\partial {\xi _1}}}} \right)} \right) $

(13)

其中，${K_x} \equiv \frac{1}{{{h_1}{h_2}}}\frac{{\partial {h_2}}}{{\partial {\xi _1}}}, {\rm{ }}{K_y} \equiv \frac{1}{{{h_1}{h_2}}}\frac{{\partial {h_1}}}{{\partial {\xi _2}}}$，公式（12）和（13）中除Laplace项，都是几何曲率项，是由于坐标网格在物理空间的不均匀性引起的。另外在任意正交曲线坐标下，平流算子和二维Laplace算子表达式如下：

$ \left\{ \begin{align} &L={{u}_{x}}\frac{\partial }{{{h}_{1}}\partial {{\xi }_{1}}}+{{u}_{y}}\frac{\partial }{{{h}_{2}}\partial {{\xi }_{2}}}+w\frac{\partial }{\partial {{\xi }_{3}}}, \\ &{{\nabla }^{2}}=\frac{1}{{{h}_{1}}{{h}_{2}}}\left(\frac{\partial }{\partial {{\xi }_{1}}}\left({{h}_{2}}\frac{\partial }{~{{h}_{1}}\partial {{\xi }_{1}}} \right)+\frac{\partial }{\partial {{\xi }_{2}}}\left({{h}_{1}}\frac{\partial }{~{{h}_{2}}\partial {{\xi }_{2}}} \right) \right). \\ \end{align} \right. $

(14)

方程组（11）至（14）就是在任意正交曲线坐标系的微分方程组，若令（${\xi _1}, {\xi _2}, {\xi _3}$）分别代表余纬$\theta $、经度λ和高度r，则有${h_1} = r$, ${h_2} = r{\rm{cos}}\theta $, ${h_3} = 1$，代入方程组（11）至（14）就可以得到方程组（1）至（3），所以球坐标系下的模式方程组（1）至（3）实际上是方程组（11）至（14）的一个特例，或者反过来方程组（11）至（14）是方程组（1）至（3）的推广。

2.2 任意正交曲线坐标下的差分方程组

由2.1节可知，如果知道一个正交曲线坐标系与笛卡尔直角坐标系之间的函数映射关系，首先计算该正交曲线坐标系的拉梅系数（也就是地图放大因子），${h_1}, {h_2}, {h_3}$, 进而得到在该正交曲线坐标系下的偏微分方程组（11）至（14）。但是在很多情况下，球面上的正交曲线网格是在一个给定空间分辨率前提下通过数值方法求解得到的，得到的只是网格点的空间坐标，而没有显式的解析表达式。在此种情形下，可以根据网格点的空间坐标得到地图放大因子的具体数值。如果在正交曲线坐标系下，离散化之后的水平网格距分别是$\Delta {\xi _1}$、$\Delta {\xi _2}$，而在物理空间对应的网格距分别是$\Delta x$、$\Delta y$。则从点（${\xi _1}, {\xi _2}, {\xi _3}$）到点（${\xi _1} + \Delta {\xi _1}, {\xi _2}, {\xi _3}$）之间的几何距离就是$\Delta x$，由公式（9）则有$\Delta x = {h_1}\Delta {\xi _1}$；同理则有$\Delta y = {h_2}\Delta {\xi _2}$。由此很容易利用在物理空间中模式的网格距$\Delta x$、$\Delta y$、$\Delta z$，将正交曲线坐标系的方程组（11）写成差分形式。不失一般性，可以令$\Delta {\xi _1}$和$\Delta {\xi _2}$等于1，则水平的地图放大因子分别为$\Delta x$、$\Delta y$。由此可以得到离散化的差分方程组，例如一个标量$\varphi $的水平梯度的微分形式和差分形式分别为

$ \nabla \varphi =\frac{1}{{{h}_{1}}}\frac{\partial \varphi }{\partial {{\xi }_{1}}}{{\boldsymbol{\xi} }_{1}}+\frac{1}{{{h}_{2}}}\frac{\partial \varphi }{\partial {{\xi }_{2}}}{{\boldsymbol{\xi} }_{2}}={{\delta }_{x}}\varphi {{\boldsymbol{\xi} }_{1}}+{{\delta }_{y}}\varphi {{\boldsymbol{\xi} }_{2}}, $

(15)

其中，${\delta _x}\varphi = \frac{{\varphi \left({{\xi _1} + {\rm{\Delta }}{\xi _1}, {\xi _2}, {\xi _3}} \right) - \varphi \left({{\xi _1}, {\xi _2}, {\xi _3}} \right)}}{{{\rm{\Delta }}x}}$和${\delta _y}\varphi = $ $\frac{{\varphi \left({{\xi _1}, {\xi _2} + {\rm{\Delta }}{\xi _2}, {\xi _3}} \right) - \varphi \left({{\xi _1}, {\xi _2}, {\xi _3}} \right)}}{{{\rm{\Delta }}y}}$为球面上沿两个正交曲线基矢量方向的差分。同理，也可以用类似的方法给出水平散度的微分和差分形式：

$ \nabla \cdot \boldsymbol{u} = \frac{1}{{{h_1}{h_2}}}\left({\frac{\partial }{{\partial {\xi _1}}}({h_2}{u_x}) + \frac{\partial }{{\partial {\xi _2}}}({h_1}{u_y})} \right) =\\ {\rm{ }}\frac{1}{{{\rm{\Delta }}y}}{\delta _x}({u_x}{\rm{\Delta }}y) + \frac{1}{{{\rm{\Delta }}x}}{\delta _y}({u_y}{\rm{\Delta }}x). $

(16)

水平Laplace算子的表达式为

$ {{\nabla }^{2}}\varphi =\frac{1}{{{h}_{1}}{{h}_{2}}}\left(\frac{\partial }{\partial {{\xi }_{1}}}\left({{h}_{2}}\frac{\partial \varphi }{~{{h}_{1}}\partial {{\xi }_{1}}} \right)+\frac{\partial }{\partial {{\xi }_{2}}}\left({{h}_{1}}\frac{\partial \varphi }{~{{h}_{2}}\partial {{\xi }_{2}}} \right) \right)=\\ \ \ \ \ \ \ \ \frac{1}{{{\rm{\Delta }}y}}{\delta _x}({\rm{\Delta }}y{\delta _x}\varphi) + \frac{1}{{{\rm{\Delta }}x}}{\delta _y}({\rm{\Delta }}x{\delta _y}\varphi). $

(17)

在离散形式下，动量方程中水平粘性项的差分形式可以写作：

$ \begin{align} &{{F}_{\text{m}x}}=\nabla \cdot {{A}_{\text{m}}}\nabla {{u}_{x}}-{{u}_{x}}({{\delta }_{x}}\left({{A}_{\text{m}}}{{K}_{x}} \right)+{{\delta }_{y}}\left({{A}_{\text{m}}}{{K}_{y}} \right)+2{{A}_{\text{m}}}{{K}_{x}}^{2}+ \\ &2{{A}_{\text{m}}}{{K}_{y}}^{2})+{{u}_{y}}\left({{\delta }_{y}}\left({{A}_{\text{m}}}{{K}_{x}} \right)-{{\delta }_{x}}\left({{A}_{\text{m}}}{{K}_{y}} \right) \right)+ \\ &\left(2{{A}_{\text{m}}}{{K}_{y}}+{{\delta }_{y}}{{A}_{\text{m}}}){{\delta }_{x}}\left({{u}_{y}} \right)-\left(2{{A}_{\text{m}}}{{K}_{x}}+{{\delta }_{x}}{{A}_{\text{m}}} \right){{\delta }_{y}}\left({{u}_{y}} \right) \right), \\ \end{align} $

(18)

$ \begin{align} &{{F}_{\text{m}y}}=\nabla \cdot {{A}_{\text{m}}}\nabla {{u}_{y}}-{{u}_{y}}({{\delta }_{y}}({{A}_{\text{m}}}{{K}_{y}})+{{\delta }_{x}}({{A}_{\text{m}}}{{K}_{x}})+ \\ &2{{A}_{\text{m}}}{{K}_{y}}^{2}+2{{A}_{\text{m}}}{{K}_{x}}^{2})+{{u}_{x}}({{\delta }_{x}}({{A}_{\text{m}}}{{K}_{y}})-{{\delta }_{y}}({{A}_{\text{m}}}{{K}_{x}}))+ \\ &(2{{A}_{\text{m}}}{{K}_{x}}+{{\text{ }\!\!\delta\!\!\text{ }}_{x}}{{A}_{\text{m}}}{{\text{ }\!\!\delta\!\!\text{ }}_{y}}({{u}_{x}})-(2{{A}_{\text{m}}}{{K}_{y}}+{{\text{ }\!\!\delta\!\!\text{ }}_{x}}{{A}_{\text{m}}}){{\text{ }\!\!\delta\!\!\text{ }}_{x}}({{u}_{x}})), \\ \end{align} $

(19)

其中，${K_x} \equiv \frac{1}{{{\rm{\Delta }}y}}{\delta _x}({\rm{\Delta }}y), {\rm{ }}{K_y} \equiv \frac{1}{{{\rm{\Delta }}x}}{\delta _y}({\rm{\Delta }}x)$；另外以上两式还考虑了粘性系数随空间的变化。总之，从形式上看，$\Delta x, \Delta y$当为常数时，上述差分方程组与局地直角系的差分方程组是等价的。但是在球面上，$\Delta x, \Delta y$一定会随经度和纬度变化，此时计算散度、涡度、水平粘性等项时，必须考虑网格的不均匀性及其所在曲面的曲率[参见方程（16）至（19）]。

LICOM2.0水平动量方程中平流项是利用中央差进行计算的，温度和盐度方程中平流项则有两种选择，一种是中央差，另外一种是保型平流计算方案。在任意正交曲线坐标下，其相应差分格式的推导过程详见附录A。

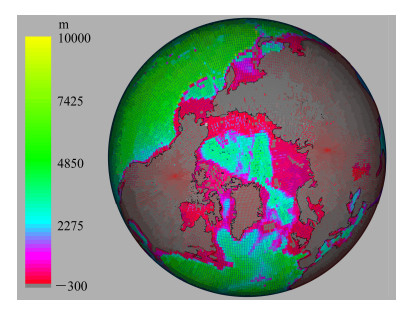
2.3 三极网格的构建

由于球面是曲率不为0的闭合曲面，数学上就不存在一一对应的映射可以将整个球面投影到一个二维欧几里得平面上，所以任何一个试图将二维球面映射到二维平面的投影一定存在所谓的奇点。例如，经纬网格的南极点和北极点就是这样的奇点，在奇点上无法定义速度，而且奇点附近纬向网格距变得很小，很难满足计算稳定性条件。由于南极点附近是陆地，因此对于海洋模式来说，北极点就是唯一的奇点。目前大多数海洋模式处理北极点的方式有两种，一种是通过投影变换将北极点旋转到陆地上，南极点的位置不变，这种办法的最主要缺陷是绝大部分模式网格与经线和纬线相互平行。三极坐标是另外一种办法，将北极点一分为二分别放在两块不同陆地上（例如，一个在北美，一个在欧亚大陆），再加上南极点就一共有三个极点。产生三极坐标的办法有很多种，本文所采用的方式是基于Madec and Imbard（1996）的工作，在北半球采用共焦点的双曲线和椭圆构造正交曲线网格，在南半球采用麦卡托投影，二者在赤道附近可以完全平滑过渡（图 1）。三极坐标在北冰洋海区可以产生比较均匀的格点，而在北冰洋以外区域网格又大致与经纬线相互平行。但是三极坐标的困难之处在于，投影到平面上的网格中最北边的那一条线，即连接上述两个焦点极点的直线，需要进行特别的处理，附录B将详细介绍具体的处理方法。

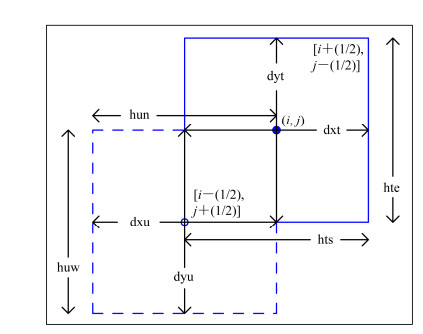
与LICOM2.0一样，本文中的动力框架依然采用B网格，变量分布见图 2。对于经纬网格的动力框架，由于任一网格单元的边界都平行于经圈或者纬圈，因此只要给出网格中心点的经纬度就可以计算出所有需要的网格参数。但是对于任意正交曲线坐标下的矩形网格系统，仅仅给出网格单元中心坐标是不够的，模式需要七个独立的水平网格参数，其中包括热力学变量网格中心经纬度（tlon、tlat）及其网格单元的西侧和南侧边长（hte和hts），动力学变量网格单元北侧和东侧边长（hun和huw），以及正交曲线基矢量与纬圈和经圈的交角（anglet）。图 2中实线为热力学变量（温度、盐度、压力等）网格单元，虚线则代表动力学变量（水平速度）网格单元。根据上述独立的网格参数，可以计算其他需要的网格参数如动力学变量中心经纬度（ulon和ulat），以及通过热力学变量和动力学变量中心的网格距（dxt、dyt、dxu和dyu）。

3 动力框架差分算法的改进 3.1 正压浅水波方程求解

同大多数原始方程海洋模式一样，LICOM一直采用正斜压分解算法。其中正压方程在B网格上采用蛙跳格式显式求解，为保证计算稳定性，还必须加上时间Asslin滤波和高纬度（66°N以北和66°S以南）纬向平滑的方法，即便如此正压积分的时间步长还是受到了极大限制。在经纬网格坐标下，1°×1°分辨率典型的正压积分步长为60 s，而在0.1°×0.1°的分辨率下，其时间步长仅仅为5 s。如果采用三极坐标，同样在大约1°×1°的分辨率下，取消高纬度纬向平滑方案，但仍旧保持Asslin滤波，时间步长最大可以取为40 s。除正压时间步长偏短之外，B网格下的正压浅水方程求解还存在显著的两倍格距波（Checkboard）现象。为此，我们采用了预估—校正的方法求解正压浅水方程组（Griffies，2009）：

$ \left\{ \begin{matrix} \frac{{{\eta }^{*}}-{{\eta }^{n}}}{\Delta t}=-\nabla \cdot {{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{b}}}}^{n}, \\ \frac{{{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{b}}}}^{n+1}-{{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{b}}}}^{n}}{\Delta t}=-gH\nabla {{\eta }^{*}}, \\ \frac{{{\eta }^{n+1}}-{{\eta }^{n}}}{\Delta t}=-\nabla \cdot {{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{b}}}}^{n+1}, \\ \end{matrix} \right. $

(20)

其中，${\eta ^*}$是预报步的海面高度，${\eta ^{n + 1}}$和${{\mathit{\boldsymbol{u}}}_{\mathit{\boldsymbol{b}}}}^{n+1}$分别是n+1时刻的海面高度和正压速度。在三极网格坐标下，使用上述预估—校正算法之后，正压浅水波方程求解既不需要采用时间方向的Asslin滤波也不需要采用纬圈方向的平滑，同时还可以显著增加积分的时间步长。例如，在1°×1°分辨率下正压积分步长可以增加到120 s，而在0.1°×0.1°的分辨率下，正压时间步长可以增加到10 s，有效地减小了正压过程的计算量。

3.2 并行算法

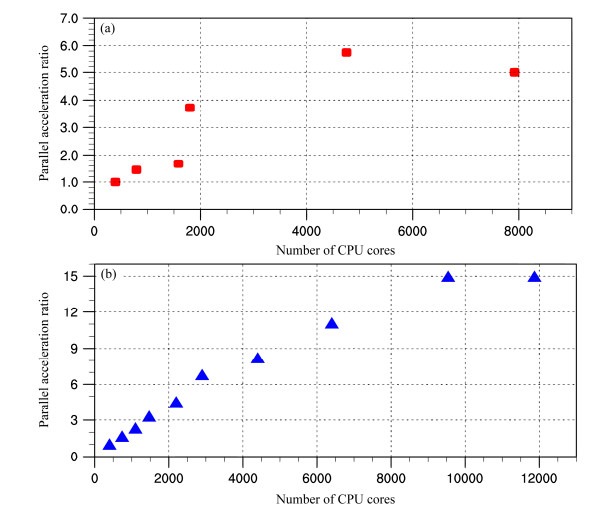
当前高性能计算机的计算速度提升主要是通过提高单个处理器速度和增加处理器规模两方面实现的，因此必须发展模式的并行计算技术，才能适应当前高性能计算机的发展趋势。另外一方面，由于单个处理器内存和计算速度的限制，也只有通过大规模的并行计算，才能保证模式空间分辨率不断提高、物理参数化过程更加精细。虽然LICOM2.0模式已经采用了MPI（Message Passing Interface）技术并行计算，但是由于只对经圈方向的格点进行一维剖分，并行规模受到了极大限制。在目前的三极网格版本中，采用了二维并行剖分技术，即对经圈和纬圈两个方向进行剖分，并行规模可以显著增加。二维剖分的具体实现如下：首先，参考POP（Parallel Ocean Program）海洋模式的做法（Smith et al., 2010），引入数据块（block）的结构。如图 3所示，假设一个二维场在纬圈和经圈方向各有nx_global和ny_global个格点，可以分别将纬圈上的格点分成nx_block等份，将经圈上的格点分成ny_block等份，这样就形成了nx_block乘以ny_block个数据块（block），每个数据块在纬圈和经圈方向各有imt和jmt个格点，并有nx_global= nx_block×imt和ny_global=ny_block×jmt。模式进行并行MPI剖分时，是针对block进行划分。一般而言，每个进程可以同时计算多个block，在一个进程中还可以针对block进行多线程（Open MP）并行。图 3给出0.1°高分辨率海洋模式经纬度网格和三极网格版本的MPI并行加速比，当模式采用经纬网格时，并行加速比在4500核时达到最大值6.0左右，超过4500核时并行效率反而下降；但当模式采用三极网格时，模式在10000核左右达到加速比的最大值16.0左右。显然三极网格的并行计算效率远远高于经纬度网格，这是因为前者没有采用高纬度的空间滤波，可以显著减小计算核心之间的通讯量，以及更容易实现不同计算核心之间的计算负载均衡。除了MPI并行技术之外，三极网格版本还采用OpenMP并行技术，在实际应用可以单独使用MPI并行，或者使用MPI与OpenMP混合并行的策略，实际测试表明后者的并行效率更高。

4 数值试验

由于上述改进的动力框架，可以适用于包括经纬网格在内任意的正交曲线坐标，本文分别针对经纬网格和三极网格设计了数值试验，检验和评估任意正交曲线坐标系下动力框架的合理性和可靠性。

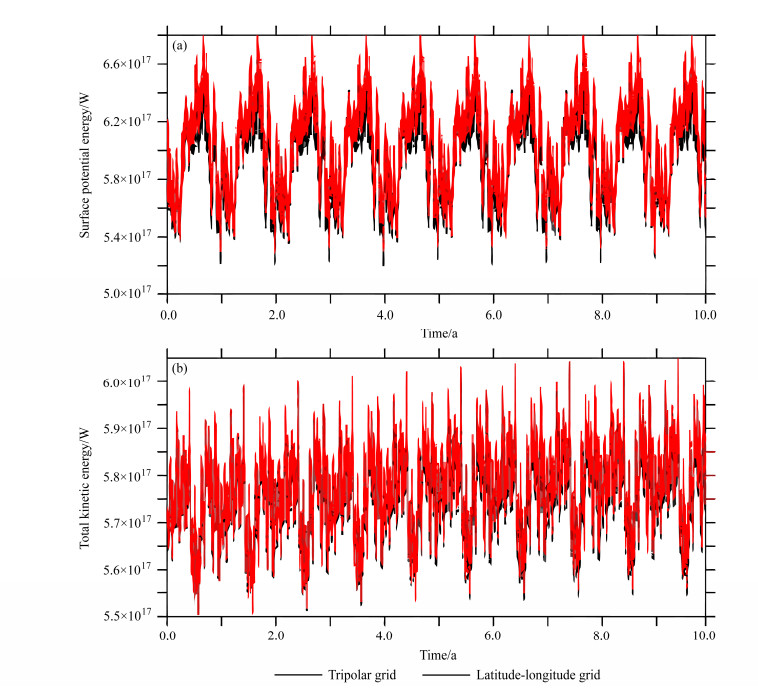
4.1 基于经纬网格的理想数值试验

由于本文中任意正交曲线坐标下的动力框架下是相对原有经纬网格动力框架的一个扩展，因此前者同时也可以应用于经纬网格，而且二者在经纬网格下应该具有一致的模拟结果。为此，我们基于LICOM2.0的经纬网格版本进行了两组数值试验，用来考察上述两种动力框架的一致性。第一组试验采用LICOM2.0经纬网格版本，其水平分辨率是1°×1°（赤道区域经向加密到0.5°），垂直分辨率为30层（Liu et al., 2012）。第二组数值试验则在LICOM2.0基础上，将本文发展的任意正交曲线坐标系下的动力框架取代原来的经纬网格动力框架，而所有的次网格物理参数化过程、模式地形、海表强迫场、初始条件以及所有其他的模式参数均保持不变。两组试验均进行了10年，图 4给出了两组试验模拟的表面位能和动能随时间变化的曲线，两组试验模拟的动能和位能的数值和变化趋势几乎完全一致。需要指出的是，虽然引进任意正交曲线坐标之后模式差分格式的具体表达式有所不同，但在数学上是可以证明对于经纬网格任意正交曲线动力框架与经纬网格框架的差分格式是完全等价的。由于差分格式的具体表达式存在差异，进行具体数值计算时两者的舍入误差也存在微小差别，这就表现为图 4中的两条曲线并不是完全一致。但是二者之间的差别是与计算机的舍入误差是相同量级的，故在不考虑计算机的舍入误差前提下，可以认为二者在经纬网格下是完全等价的。

4.2 基于三极网格的数值试验

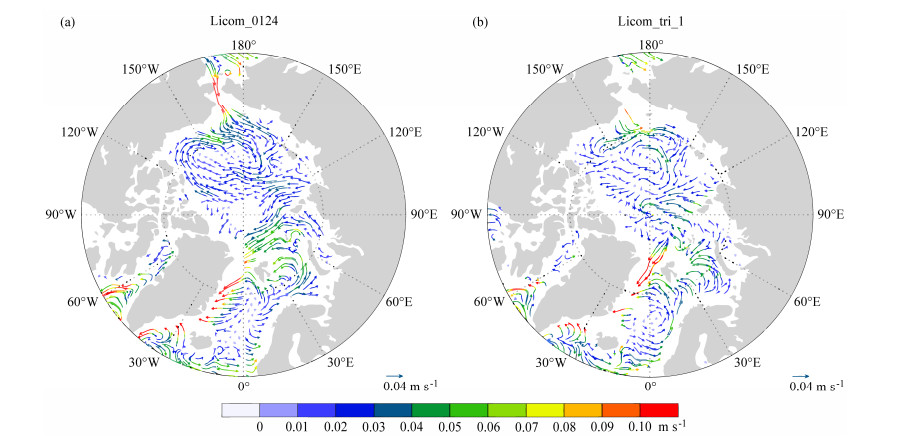
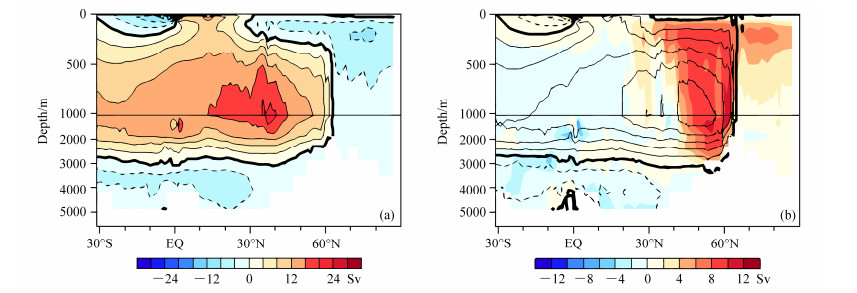
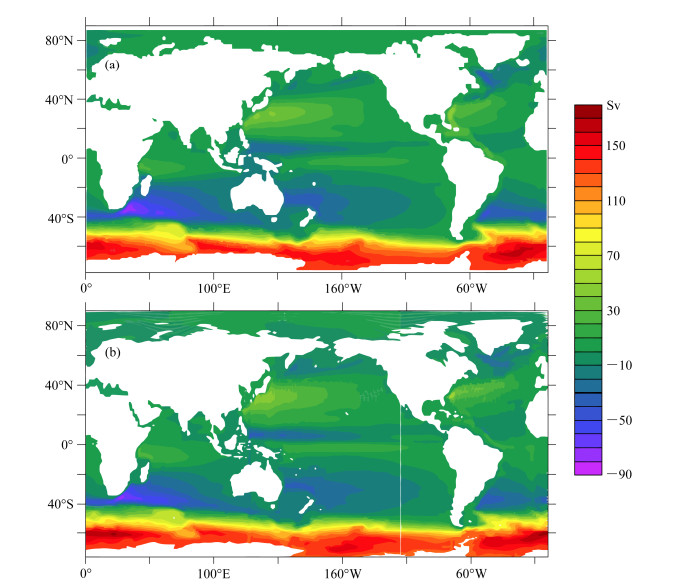
在4.1节中的第二组数值试验基础上，我们进一步修改了LICOM2.0中的地形输入文件，用三极网格地形替代原本的经纬网格地形，进行数值试验。与LICOM2.0经纬网格版本的数值试验相比，主要变化有二，一是地形特别是北冰洋区域的地形显著不同，在经纬网格版本中北极点是一块孤立的陆地，在三极网格版本中北极点附近都是海洋，与实际情况一致；其次，在三极网格版本中，极点附近的网格距相对比较均匀，因此不需要任何空间滤波来保证计算的稳定性，但是在经纬网格版本中必须采用纬圈滤波。本文分别将LICOM2.0的经纬网格版本和三极网格版本积分了500年，图 5给出了最后100年气候平均的海表流场以及观测的海表流场。由于在经纬网格版本中北极点作为孤岛处理，模式无法模拟出观测中穿越极地的海流，但是在三极网格版本中采用正确的模式地形就可以模拟穿极海流。对照观测的北极海表环流（AMAP, 1998），新的三极网格能较好的模拟出穿越极点的海流，太平洋一侧加拿大海盆顺时针旋转的波弗特涡旋，以及大西洋一侧格陵兰东部逆时针旋转的气旋涡。进一步分析还发现，由于地形和其他因素的作用，三极网格版本还可以更好地模拟北大西洋深对流的强度和位置，以及更强的的经圈翻转环流（简称MOC；图 6），特别是在经纬网格版本中由于极地孤岛的存在，模式在北冰洋海区模拟出一个逆时针的虚假环流，这与观测事实和世界上大部分海洋模式模拟结果都不一致。三极版本对垂直经圈环流的改进主要还是与地形和高纬度滤波有关，有关经圈翻转环流改进的详细分析和讨论见Li et al.（2017）。图 7给出了两个版本模拟的气候平均正压流函数，二者对世界上主要的水平环流系统如副极地涡旋、副热带大涡等的强度和位置基本一致，这是因为风生环流系统是风应力强迫的结果，而且远离北极点，因此三极网格的引入对其影响不大。

5 总结

针对中国科学院大气物理研究所全球海洋环流模式LICOM2.0在北冰洋附近海区的模拟偏差，本文基于模式原始方程组，在保证与LICOM2.0中经纬网格动力框架一致性的前提下，发展了一个可以适用于包括经纬网格在内的任意水平正交曲线坐标系的海洋模式动力框架。然后，将改进后的动力框架应用于LICOM2.0，分别采用经纬网格和三极网格进行数值试验，与LICOM2.0经纬网格版本模拟结果进行对比，评估了动力框架的可靠性及其对模式性能的影响。

采用相同的经纬网格坐标系，以及在完全一致的模式地形、物理参数、强迫场和初始条件下，在不考虑计算机舍入误差的前提下，改进以后的动力框架与LICOM2.0原有的动力框架模拟结果可以保证完全一致，证明了动力框架的合理性和可靠性。基于新的动力框架，海洋模式可以采用能够准确描述北冰洋地形的三极网格，克服了LICOM2.0经纬网格版本必须将北极点处理为孤岛的缺陷，从而显著改进了模式对于北冰洋环流和北大西洋经圈翻转流函数的模拟能力。与此同时，引进三极网格还可以避免模式网格距随维度增加急剧减小带来的计算稳定性问题，在LICOM2.0的三极网格版本中，模式不需要采用任何空间滤波方案仍然能够保证计算的稳定性，从而与LICOM2.0的经纬网格版本相比，极大地提高了模式的并行效率，这一点在水平分辨率提高到0.1°时表现得尤为明显，海洋模式的并行加速比可以从经纬网格版本的5.8左右提高到三极网格版本的15.0左右。

附录A 任意正交曲线坐标系下的平流项差分格式 A.1 中央差方案

以温度方程为例，在n时刻x和y方向平流项${\rm{ad}}{{\rm{v}}_x}$和${\rm{ad}}{{\rm{v}}_y}$分别可以写作：

$ {\rm{ad}}{{\rm{v}}_x} = 0.5 \times ({u_{w{\rm{face}}}}_{i + 1, j}^n \times (T_{i + 1, j}^{n - 1} - T_{i, j}^{n - 1}) + {u_{w{\rm{face}}}}_{i, j}^n{\rm{*}}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (T_{i, j}^{n - 1} - T_{i - 1, j}^{n - 1})) \times T{\rm{are}}{{\rm{a}}_r}_{i, j}, $

(A.1)

$ {\rm{ad}}{{\rm{v}}_y} = 0.5 \times ({v_{{\rm{sface}}}}_{i, j - 1}^n \times (T_{i, j}^{n - 1} - T_{i, j - 1}^{n - 1}) + {v_{{\rm{sface}}}}_{i, j}^n \times \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\rm{(}}T_{i, j + 1}^{n - 1} - T_{i, j}^{n - 1}{\rm{)}}) \times T{\rm{are}}{{\rm{a}}_r}_{i, j}, $

(A.2)

其中，${u_{w{\rm{face}}}}_{i, j}^n$和${v_{s{\rm{face}}}}_{i, j}^n$分别为n时刻温盐网格单元西侧和南侧的速度与相应边长的乘积：

$ {u_{w{\rm{face}}}}_{i, j}^n = 0.5 \times \left({u_{i, j - \frac{1}{2}}^n + u_{i, j + \frac{1}{2}}^n} \right) \times {\rm{ht}}{{\rm{w}}_{i, j}}, $

(A.3)

$ {v_{s{\rm{face}}}}_{i, j}^n = 0.5 \times \left({v_{i, j + \frac{1}{2}}^n + v_{i + 1, j + \frac{1}{2}}^n} \right) \times {\rm{ht}}{{\rm{s}}_{i, j}}, $

(A.4)

$T_{i, j}^{n - 1}$则为n－1时刻的温度，而$T{\rm{area}}\_{r_{i, j}}$为该网格单元面积的倒数。由于垂直方向也采用交错网格，垂直速度$w_k^n$在整数层k上，温度$T_{k + 1/2}^n$位于半层k+1/2处，这里k=0, 1, 2…。由此在k+1/2处的垂直平流可以写为

$ {\rm{ad}}{{\rm{v}}_z} = 0.5 \times {\rm{(}}w_k^n \times {\rm{(}}T_{k - \frac{1}{2}}^{n - 1} - T_{k + \frac{1}{2}}^{n - 1}{\rm{)}} + w_{k + 1}^n \times {\rm{(}}T_{k + \frac{1}{2}}^{n - 1} - T_{k + \frac{3}{2}}^{n - 1}{\rm{))}} \times \frac{1}{{\Delta {Z_k}}}. $

(A.5)

A.2 保型平流差分方案

本文将Yu（1994）提出的保型平流方案扩展到任意的正交曲线坐标系下，该格式综合了Lax- Wendroff和迎风差两种格式的优点，可以保证物质平流输送的正定性。首先根据按照Lax-Wendroff格式，纬向平流可以分为如下三部分：

$ {\rm{ad}}{{\rm{v}}_{x1}} = 0.5 \times ({u_{w{\rm{face}}}}_{i + 1, j}^n \times {\rm{(}}T_{i + 1, j}^{n - 1} + T_{i, j}^{n - 1}{\rm{)}} - \\ {u_{w{\rm{face}}}}_{i, j}^n \times (T_{i, j}^{n - 1} + T_{i - 1, j}^{n - 1})) \times T{\rm{area}}\_{r_{i, j}}, $

(A.6)

$ {\rm{ad}}{{\rm{v}}_{x2}} = 0.5 \times \Delta t \times {u_{w{\rm{face}}}}_{i + 1, j}^n \times {u_{w{\rm{face}}}}_{i + 1, j}^n \times (T_{i + 1, j}^{n - 1} - T_{i, j}^{n - 1})/ \\ \ \ \ \ \ \ \ \ \ \ \ (ht{w_{i + 1, j}} \times hu{n_{i + 1, j}}) \times T{\rm{area}}\_{r_{i, j}}, $

(A.7)

$ {\rm{ad}}{{\rm{v}}_{x3}} = - 0.5 \times \Delta t \times {u_{w{\rm{face}}}}_{i, j}^n \times {u_{w{\rm{face}}}}_{i, j}^n \times (T_{i, j}^{n - 1} - T_{i - 1, j}^{n - 1})/\\ \ \ \ \ \ \ \ \ \ \ \ (ht{w_{i, j}} \times hu{n_{i, j}})) \times T{\rm{area}}\_{r_{i, j}}, $

(A.8)

其中，${u_{wface}}_{i, j}^n$，$T_{i, j}^{n - 1}$等项的物理含义可以参见附录A.1。由此，可以给出预估步温度${T^*}$为

$ {T^*}_{i, j} = \left({{\rm{ad}}{{\rm{v}}_{x1}} + {\rm{ad}}{{\rm{v}}_{x2}} + {\rm{ad}}{{\rm{v}}_{x3}}} \right) \times \Delta t, $

(A.9)

然后判断相对于n－1步的温度，预估的温度值是否产生了新的局部极值，即对于任何一个点上的预估值${T^{\rm{*}}}_{i, j}$，与附近三个格点（$T_{i - 1, j}^{n - 1}, T_{i, j}^{n - 1}, T_{i + 1, j}^{n - 1}$）温度值进行比较，如果${T^*}_{i, j}$大于这三个点中的最大值或者小于其中的最小值，就认为预估值${T^*}_{i, j}$是新的极值。如果预估值${T^*}_{i, j}$和${T^*}_{i + 1, j}$都不是新的极值，${\rm{ad}}{{\rm{v}}_{x2}}$的表达式保持不变，否则将${\rm{ad}}{{\rm{v}}_{x2}}$写作：

$ {\rm{ad}}{{\rm{v}}_{x2}} = 0.5 \times (\left| {{u_{wface}}_{i + 1, j}^n} \right| \times T_{i + 1, j}^{n - 1} - T_{i, j}^{n - 1})/{\rm{hu}}{{\rm{n}}_{i + 1, j}} \times .\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ T{\rm{area}}\_{r_{i, j}}. $

(A.10)

同样，如果预估值${T^*}_{i, j}$和${T^*}_{i - 1, j}$都不是新的极值，${\rm{ad}}{{\rm{v}}_{x3}}$的表达式保持不变，否则将${\rm{ad}}{{\rm{v}}_{x3}}$写作：

${\rm{ad}}{{\rm{v}}_{x3}} = - 0.5 \times \left| {{u_{w{\rm{face}}}}_{i, j}^n} \right| \times T_{i, j}^{n - 1} - T_{i - 1, j}^{n - 1})/{\rm{hu}}{{\rm{n}}_{i, j}} \times T{\rm{area}}\_{r_{i, j}}. $

(A.11)

与上式类似，同样还可以写出经向和垂直平流的差分格式。

附录B 三极网格极点处理方案

所谓的网格极点是指经过坐标变换之后的计算网格系统的极点，这样网格极点一共有三个。最南端的网格极点与地理上的南极点重合，经过坐标变换之后这个点在实际计算网格系统中对应的是一条直线，与经纬网格中的处理完全一样。计算网格最北端有两个网格极点，例如在1°×1° LICOM版本中这两个点的地理经度、纬度分别为（65°N，65°E）和（65°N，115°W）。

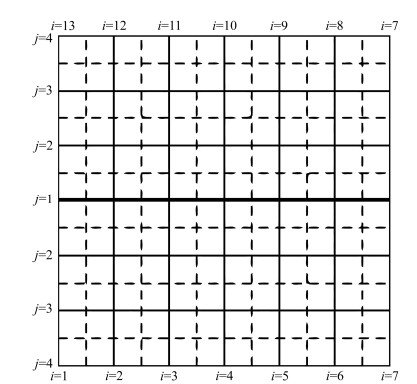
图 B1是三极坐标网格在北极附近的示意图，假设每排有12个网格单元，这里给出了前4排格点（j=1, 4）的排列方式。为了反映能够较为真实地北极附近格点之间的相对位置关系，该示意图将最北边一排格点对折。其中两个网格极点在示意图中分别位于（i=1，j=1）以及（i=7，j=1)处，而地理上的北极点则位于（i=4，j=1）处。从物理上说，第一排格点是三极坐标网格系统的缝合线，在缝合线上标量是关于网格极点是对称的，矢量则是反对称的。但是具体进行数值计算时，每个点上的变量都是单独计算的，为保证物理上的一致性，模式在每一步都会强制缝合线上的物理量保证对称或者反对称。

附录C 经向热输送和经圈翻转流函数诊断分析

经向热输送和经圈翻转流函数可以描述海洋环流在经圈方向的热量和质量输送，是气候系统的基本诊断统计变量之一。在经纬网格版本中，经向速度是模式的预报变量，可以直接用于经向热输送和经圈流函数的诊断分析。但是，在三极网格版本中，速度矢量并不总是与经圈和纬圈平行，因此需要改进经向热输送和经圈翻转流函数的诊断分析方法，具体计算方案如下。

C.1 经圈翻转流函数（MSF）

在经纬网格坐标系统下，经圈流函数（MSF）计算公式如下：

$ {\rm{MSF}}(y, z) = \int_0^z {\int_{x{\rm{e}}}^{x{\rm{w}}} {(v\left({x, y, z} \right) + {v_{{\rm{eddy}}}}(x, y, z)){\rm{d}}x{\rm{d}}z, } } $

(C.1)

其中，$v\left({x, y, z} \right)$代表欧拉经向速度，${v_{{\rm{eddy}}}}$为中尺度涡旋诱导的速度，x_e和x_w是纬向积分东西边界的经度，可以是从一个海盆东西边界所在经度，或者代表整个纬圈的积分，因此上述积分可以应用于全球或者某一个洋盆。但是当模式采用任意正交曲线坐标，模式中的v并不总是代表经向速度，因此此时需要利用垂直速度诊断MSF，参考POP海洋模式的诊断方法（Smith et al. 2010），计算公式如下：

$ {\rm{MSF}}\left({y, z} \right) = {\rm{MSF}}\left({s\_{\rm{lat}}, z} \right) + \int_{s\_{\rm{lat}}}^y {\int_{x{\rm{e}}}^{x{\rm{w}}} {(w\left({x, y, z} \right) + } } \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {w_{{\rm{eddy}}}}(x, y, z)){\rm{d}}x{\rm{d}}z. $

(C.2)

与公式（C.1）不同的是，（C.2）式利用欧拉垂直速度w和中尺度涡旋诱导的垂直速度${w_{{\rm{eddy}}}}$计算MSF时需要进行经向积分，因此需要给出南边界处的初值。如果计算全球MSF，需要从南极大陆开始向北积分，根据经圈流函数的定义，在边界处流函数为0，即${\rm{MSF}}\left({s\_{\rm{lat}}, z} \right) = 0$。但是如果计算大西洋海盆的MSF，南边界一般放在32°S左右，此时南边界上的流函数并不为0。由于三极网格在南半球采用的是墨卡托投影，海流速度矢量方向与经圈和纬圈平行，因此这时必须首先利用公式（C.1）根据模拟的经向速度计算在MSF在32°S处的初值，然后再利用公式（C.2）从南边界开始向北积分得到北大西洋海盆的MSF。另外，需要注意的是，由于模式中水平网格与经纬网格并不相互平行，因此为了实现公式（C.2）中的经圈积分，必须首先定义一个人为的纬度网格lat_aux，然后基于lat_aux进行经向积分，计算全球或者区域海盆的MSF。

C.2 经向热量（MTH）和淡水输送（MTF）

在经纬网格系统下，经向热输送（MTH）可以用下面的公式计算：

$ {\rm{MTH}}\left(y \right) = \rho {c_P}\int_{x{\rm{e}}}^{x{\rm{w}}} {\int_0^H {v\left({x, y, z} \right)T\left({x, y, z} \right){\rm{d}}x{\rm{d}}z + } } \rho {c_P} \cdot \\ \int_{x{\rm{e}}}^{x{\rm{w}}} {\int_0^H {{v_{{\rm{eddy}}}}\left({x, y, z} \right)T\left({x, y, z} \right){\rm{d}}x{\rm{d}}z + \rho {c_P}\int_{x{\rm{e}}}^{x{\rm{w}}} {\int_0^z {k\frac{{\partial T(x, y, z)}}{{\partial y}}{\rm{d}}x{\rm{d}}z, } } } } $

(C.3)

类似地，经向淡水输送可以写为

$ {\rm{MTF}}\left(y \right) = \int_{x{\rm{e}}}^{x{\rm{w}}} {\int_0^H {v\left({x, y, z} \right)(S\left({x, y, z} \right) - {S_0}){S_0}^{ - 1}{\rm{d}}x{\rm{d}}z + } } \\ \ \ \ \ \ \int_{x{\rm{e}}}^{x{\rm{w}}} {\int_0^H {{v_{{\rm{eddy}}}}\left({x, y, z} \right)(S\left({x, y, z} \right) - {S_0}){S_0}^{ - 1}{\rm{d}}x{\rm{d}}z + } }\\ \ \ \ \ \ \int_{x{\rm{e}}}^{x{\rm{w}}} {\int_0^z {k\frac{{\partial S(x, y, z)}}{{\partial y}}{S_0}^{ - 1}{\rm{d}}x{\rm{d}}z} }, $

(C.4)

其中，$v\left({x, y, z} \right)$和${v_{{\rm{eddy}}}}\left({x, y, z} \right)$为欧拉经向速度和中尺度涡旋诱导的经向速度，$T\left({x, y, z} \right)$为温度。

在任意正交曲线作标下，由于v不一定是代表经向速度，所以无法用模式计算的v直接估计经向热输送。但是，我们可以估计由平流、中尺度涡旋和扩散过程导致的加热倾向在水平和垂直方向进行积分，估计以上过程对南北方向热输送的贡献。与计算经向翻转流函数类似，我们仍然需要定义人为的纬度网格lat_aux，然后基于lat_aux由南向北积分估计热量和淡水的经向输送。估计全球的经向输送，从南极大陆开始积分，南边界条件为0；如果估计大西洋海盆的热量和淡水经向输送，必须首先给定南边界的边界条件，其边界条件的估计与计算经向翻转流函数边界条件的估计类似。

$ {\rm{MHT}}(y) = \rho {c_P}\int_{S\_{\rm{lat}}}^y {\int_0^H {\int_{x{\rm{e}}}^{x{\rm{w}}} {{\rm{adv}}\_T(x, y, z){\rm{d}}x{\rm{d}}z{\rm{d}}y + } } }\\ \rho {c_P}\int_{S\_{\rm{lat}}}^y {\int_0^H {\int_{x{\rm{e}}}^{x{\rm{w}}} {{\rm{ad}}{{\rm{v}}_{{\rm{eddy}}}}\_T(x, y, z){\rm{d}}x{\rm{d}}z{\rm{d}}y + } } }\\ \rho {c_P}\int_{S\_{\rm{lat}}}^y {\int_0^H {\int_{x{\rm{e}}}^{x{\rm{w}}} {{\rm{diff}}\_T(x, y, z){\rm{d}}x{\rm{d}}z{\rm{d}}y} } }, $

(C.5)

${\rm{MFT}}(y) = \int_{S\_{\rm{lat}}}^y {\int_0^H {\int_{x{\rm{e}}}^{x{\rm{w}}} {{\rm{adv}}\_S(x, y, z){S_0}^{ - 1}{\rm{d}}x{\rm{d}}z{\rm{d}}y + } } }\\ \ \ \ \ \ \int_{S\_{\rm{lat}}}^y {\int_0^H {\int_{x{\rm{e}}}^{x{\rm{w}}} {{\rm{ad}}{{\rm{v}}_{{\rm{eddy}}}}\_S(x, y, z){S_0}^{ - 1}{\rm{d}}x{\rm{d}}z{\rm{d}}y + } } } \\ \ \ \ \ \ \int_{S\_{\rm{lat}}}^y {\int_0^H {\int_{x{\rm{e}}}^{x{\rm{w}}} {{\rm{diff}}\_S(x, y, z){S_0}^{ - 1}{\rm{d}}x{\rm{d}}z{\rm{d}}y} } } . $

(C.6)

致谢: 感谢匿名审稿人对本文的宝贵建议。