引用本文

沈新勇, 沙莎, 李小凡, 等. 2018. 一次梅雨锋暴雨过程中多尺度能量相互作用的研究Ⅰ.理论分析 [J]. 大气科学, 42(5): 1109-1118.

Shen Xinyong, Sha Sha, Li Xiaofan, et al. 2018. The Study of Multi-scale Energy Interactions during a Meiyu Front Rainstorm. Part Ⅰ: Theoretical Analysis [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 42(5): 1109-1118, doi:10.3878/j.issn.1006-9895.1710.17195.

一次梅雨锋暴雨过程中多尺度能量相互作用的研究Ⅰ.理论分析
沈新勇
1,2
,
沙莎
1,3,
李小凡
4
1 南京信息工程大学气象灾害教育部重点实验室/气候与环境变化国际合作联合实验室/气象灾害预报预警与评估协同创新中心, 南京 210044
2 中国科学院大气物理研究所云降水物理与强风暴重点实验室, 北京 100029
3 上海海洋气象台, 上海 201306
4 浙江大学地球科学学院, 杭州 310027
收稿日期: 2017-07-22; 网络预出版日期: 2017-11-16
资助项目: 国家自然科学基金项目41530427、41790471、41475039,国家重点基础研究发展计划(973计划)项目2015CB453201
摘要:
本文是讨论梅雨锋暴雨过程中多尺度能量相互作用问题的开始部分。为了分析梅雨锋暴雨过程中的多尺度能量相互作用,从z坐标系中的运动方程和热力学方程出发,把基本物理量分成大尺度背景场(>2000 km)、α中尺度(200~2000 km)和β中小尺度系统(< 200 km)分量,利用滞弹性近似,推导了大尺度背景场、α中尺度和β中小尺度系统三个尺度的动能方程和位能方程。能量方程中包含了各尺度动能之间的转换、位能之间的转换以及动能和位能之间的转换。动能方程主要包括各尺度动能之间转换项、动能输送项、水平气压梯度力做功项、垂直方向扰动气压梯度力做功项、浮力做功项、地转偏向力分量做功项以及摩擦力做功项。位能方程主要包括各尺度位能之间转换项、位能输送项、浮力做功项以及非绝热加热做功项。其中浮力做功项为位能和动能之间的能量转换项,是暴雨发生发展过程中比较关键的能量转换项。关于将能量方程用于梅雨锋暴雨过程中并且诊断能量相互作用影响暴雨发展和消亡过程的物理机制等问题,将在以后的研究中给出。
关键词:
大尺度背景场
α中尺度
β中小尺度
动能和位能方程
相互作用
The Study of Multi-scale Energy Interactions during a Meiyu Front Rainstorm. Part Ⅰ: Theoretical Analysis
SHEN Xinyong
1,2
,
SHA Sha
1,3,
LI Xiaofan
4
1 Key Laboratory of Meteorological Disaster, Ministry of Education/Joint International Research Laboratory of Climate and Environment Change/Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044
2 Key Laboratory of Cloud-Precipitation Physics and Severe Storms, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
3 Shanghai Marine Meteorological Center, Shanghai 201306
4 School of Earth Sciences, Zhejiang University, Hangzhou, Zhejiang 310027
Funded by: National Natural Science Foundation of China (Grants 41530427, 41790471, 41475039), National Basic Research Program of China (973 Program) (Grant 2015CB453201)
Abstract:
This paper is the beginning part of the discussion on the multi-scale energy interactions in the Meiyu front rainstorm. The kinetic energy equations and potential energy equations of large scale background field, meso-α scale and meso-micro-β scale are derived from motion equations and thermodynamic equations in the z coordinate system using the anelastic approximation by dividing the basic physical quantity into three scales for the purpose to analyze the multi-scale energy interactions. Various energy conversions are presented in the energy equations. The kinetic energy equations mainly include kinetic energy transportation or conversion, the work of horizontal pressure gradient force, vertical perturbation pressure gradient force, buoyancy, Coriolis force and friction. The potential energy equations mainly include potential energy transportation or conversion, and the effects of buoyancy and diabetic heating. Among them, the effect of buoyancy is substantially the energy conversion term between the potential energy and kinetic energy, and thus is the most critical energy conversion term in the process of rainstorm development. In the future study, the energy equations will be applied to the Meiyu front rainstorm, and the physical mechanism for the diagnosed energy interaction, which affects the development and disappearance of rainstorm, will be given.
Keywords:
Large scale background field
Meso-α scale
Meso-micro-β scale
Kinetic energy and potential energy equation
Interaction
1 引言
梅雨锋暴雨是梅雨期典型的洪涝灾害。由于梅雨期会发生大范围持续性暴雨和集中的特大暴雨,所以研究梅雨期暴雨有着重要的科学和社会意义。
1955年,Lorenz(1955)把总势能与最小总势能的差值定义为位能,随密度或者温度水平梯度的存在而存在。在绝热过程中,位能和动能的总和为常数。洛伦兹还将大气物理量分解成平均场和扰动场,当低纬的暖空气和高纬的冷空气相遇,平均场会将部分能量转换给扰动场,具体为平均位能将部分能量转换给扰动位能,扰动位能再将部分能量转换给扰动动能,最后扰动动能将能量转换给平均动能,这就是著名的洛伦兹能量循环。1957年,Saltsman(1957)通过对行星尺度的运动采用傅里叶级数分析来定义运动的尺度,再进行各个尺度能量方程的推导,推导的能量方程中包含特定波数域中涡旋气流和平均气流的位能的产生、释放和向动能的能量转换等。1983年,Plumb(1983)在转换欧拉平均(Andrews and McIntyre, 1976)的基础上从原始方程出发对能量方程的推导做出了一些改进,推导出的能量方程中不仅包含平均动能向涡动动能转换之类的项,还包含了能量通量这样的输送项。1984年,Kanzawa(1984)也在转换欧拉平均的基础上从准地转方程出发作出进一步的研究,发现平均位能和扰动位能之间不存在能量转换。2000年以前,不同的学者在不同的条件下从欧拉观点出发推导了各种能量方程。这之后,Iwasaki(2001)从拉格朗日经圈环流的角度出发在等熵坐标系中推导位能和动能变率方程来解释波流相互作用,研究表明在经度—高度剖面上没有平均动能和扰动动能的能量转换;进一步研究发现平均气流波数增加,平均动能向扰动位能转换能量,平均气流波数减小,扰动位能向扰动动能转换能量。2010年,Murakami(2010)提出了一个新的局地能量诊断方案,与之前不同的是,能量方程不仅包含平均能量方程和扰动能量方程,还包含了一个新的能量方程,即相互作用能量方程。当采取适当平均之后,相互作用能量可能会消失,但相互作用能量的方程不会消失,并且将相互作用能量通量和两类能量转换项有机地建立关系,丰富和完善了洛伦兹经典的能量循环图。这几十年以来,几乎所有学者都是以平均场和扰动场为研究对象去探讨能量之间的相互作用或能量循环。很少有学者探讨三个尺度及其以上之间的能量学特征,2011年,Hsu et al.(2011)在p坐标系中推导了三个尺度下的动能方程,用于研究夏季季节内震荡和天气尺度扰动之间的相互作用,这是能量学的一大突破。
近几年来,从能量学的角度去定量分析梅雨锋暴雨过程开始逐渐盛行,很多学者把大尺度看成基本量,把中尺度看成是扰动量,利用能量方程来探究大尺度与中尺度系统这两种尺度之间的相互作用。但直接触发暴雨生成的最主要的系统是中尺度系统中的β中尺度和γ中尺度扰动(王建捷和李泽椿,2002;廖移山等,2010;孙晶,2011),如果用两个尺度能量方程来研究梅雨锋暴雨过程中多尺度系统之间的相互作用不能显著突出中小尺度系统对暴雨生成的重要作用。所以本文为了分析梅雨锋暴雨过程中的多尺度能量相互作用,在第一部分推导了z坐标系中大尺度背景场(>2000 km)、α中尺度(200~2000 km)和β中小尺度系统(<200 km)三个尺度的动能方程和位能方程。在以后的研究中将深入探究大尺度背景场、α中尺度和β中小尺度系统之间的相互作用对暴雨发生发展的影响,以期对暴雨天气的预报有一定的指示意义。
2 能量方程的推导
2.1 三个原始的运动方程和热力学方程
z坐标系中的原始方程(出发方程):
|
$
\frac{{{\rm{d}}u}}{{{\rm{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + fv + \upsilon (\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}),
$
|
(1) |
|
$
\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} - fu + \upsilon (\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}}),
$
|
(2) |
|
$
\frac{{{\rm{d}}w}}{{{\rm{d}}t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} - g + \upsilon (\frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{{{\partial ^2}w}}{{\partial {y^2}}} + \frac{{{\partial ^2}w}}{{\partial {z^2}}}),
$
|
(3) |
|
$
\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = \frac{\theta }{{{c_{\rm{p}}}T}}\dot Q,
$
|
(4) |
其中,u、v和w分别是纬向、经向和垂直方向上的风速,p为气压,ρ为密度,θ为位温,T为气温,f为地转参数,g为重力加速度,υ为运动学粘滞系数,Q表示非绝热加热,cp是空气的定压比热。在上述方程计算密度和位温时,涉及到的公式还有状态方程和位温方程:
|
$
\theta =T{{\left( \frac{1000}{p} \right)}^{{R}/{{{c}_{p}}}\;}},
$
|
(6) |
其中,R为比气体常数。
将物理量分解成“ $ {\bar{A}}$
”、“${\tilde{A}} $”和“ $\widetilde{A} $
”三个尺度分量,“ $ {\bar{A}}$
”表示空间尺度为2000 km以上的大尺度背景场,“ ${\tilde{A}} $
”表示空间尺度为200~2000 km之间的α中尺度系统,“ ${{A}'} $
”表示空间尺度为200 km以下的β中尺度和γ中尺度等中小尺度系统,那么$ u=\overline{u}+\tilde{u}+{u}'$,$v=\overline{v}+\tilde{v}+{v}' $,$w=\overline{w}+\tilde{w}+{w}' $;$ T=\overline{T}+\tilde{T}+{T}'$,$\theta =\overline{\theta }+\tilde{\theta }+{\theta }' $,$p=\overline{p}+\tilde{p}+{p}' $,$ \rho =\overline{\rho }+\tilde{\rho }+{\rho }'$。
由于长时间暴雨过程是中尺度深对流过程,所以利用滞弹性近似公式(7)(寿绍文,2009)对垂直运动方程进行处理,它与原始方程的不同是保留了平均密度的垂直变化,即保留了压缩效应和热膨胀效应引起的密度变化,考虑了由密度扰动引起的浮力,比较接近实际流体。
|
$
\frac{{\tilde \rho + \rho '}}{{\overline \rho }} = \frac{{{c_v}}}{{{c_p}}}\frac{{\tilde p + p'}}{{\overline p }} - \frac{{\tilde \theta + \theta '}}{{\overline \theta }},
$
|
(7) |
其中,cp是空气的定压比热,cv是空气的定容比热。
垂直方向运动方程变成:
|
$
\begin{array}{l}
\frac{{{\rm{d}}w}}{{{\rm{d}}t}} = - \frac{1}{{\overline \rho }}\frac{{\partial (\tilde p + p')}}{{\partial z}} - \frac{{\tilde \rho + \rho '}}{{\overline \rho }}g + \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}}\frac{{\partial (\tilde p + p')}}{{\partial z}} = \\
- \frac{1}{{\overline \rho }}\frac{{\partial (\tilde p + p')}}{{\partial z}} + \frac{{\tilde \theta + \theta '}}{{\overline \theta }}g - \frac{{{c_v}}}{{{c_p}}}\frac{{\tilde p + p'}}{{\overline p }}g + \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}}\frac{{\partial (\tilde p + p')}}{{\partial z}}.
\end{array}
$
|
(8) |
2.2 动能方程的推导
2.2.1 计算u′×公式(1)+v′×公式(2)+w′×公式(8),求$ {\partial {K}'}/{\partial \ t}\;$
|
$
\begin{array}{*{35}{l}}
\partial {K}'/\partial t={{a}_{1}}+{{a}_{2}}+{{a}_{3}}+{{a}_{4}}+{{a}_{5}}+{{a}_{6}}+{{a}_{7}}+{{a}_{8}}+{{a}_{9}}+ \\
{{a}_{10}}+{{a}_{11}}+{{a}_{12}}+{{a}_{13}}+{{a}_{14}}+{{a}_{15}}+{{a}_{16}}+{{a}_{17}}+{{a}_{18}}+ \\
{{a}_{19}}+{{a}_{20}}+{{a}_{21}}, \\
\end{array}
$
|
(9) |
|
$
{a_1} = - \left[ {u'(\frac{{\partial \overline u }}{{\partial t}} + \frac{{\partial \tilde u}}{{\partial t}}) + v'(\frac{{\partial \overline v }}{{\partial t}} + \frac{{\partial \tilde v}}{{\partial t}}) + w'(\frac{{\partial \overline w }}{{\partial t}} + \frac{{\partial \tilde w}}{{\partial t}})} \right],
$
|
(10) |
|
$
{a_2} = - \left(\begin{array}{l}
u'\overline u \frac{{\partial \overline u }}{{\partial x}} + v'\overline u \frac{{\partial \overline v }}{{\partial x}} + w'\overline u \frac{{\partial \overline w }}{{\partial x}} + u'\overline v \frac{{\partial \overline u }}{{\partial y}} + v'\overline v \frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}w'\overline v \frac{{\partial \overline w }}{{\partial y}} + u'\overline w \frac{{\partial \overline u }}{{\partial z}} + v'\overline w \frac{{\partial \overline v }}{{\partial z}} + w'\overline w \frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(11) |
|
$
{a_3} = - \left(\begin{array}{l}
u'\tilde u\frac{{\partial \overline u }}{{\partial x}} + v'\tilde u\frac{{\partial \overline v }}{{\partial x}} + w'\tilde u\frac{{\partial \overline w }}{{\partial x}} + u'\tilde v\frac{{\partial \overline u }}{{\partial y}} + v'\tilde v\frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}w'\tilde v\frac{{\partial \overline w }}{{\partial y}} + u'\tilde w\frac{{\partial \overline u }}{{\partial z}} + v'\tilde w\frac{{\partial \overline v }}{{\partial z}} + w'\tilde w\frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(12) |
|
$
{a_4} = - \left(\begin{array}{l}
u'u'\frac{{\partial \overline u }}{{\partial x}} + v'u'\frac{{\partial \overline v }}{{\partial x}} + w'u'\frac{{\partial \overline w }}{{\partial x}} + u'v'\frac{{\partial \overline u }}{{\partial y}} + v'v'\frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}w'v'\frac{{\partial \overline w }}{{\partial y}} + u'w'\frac{{\partial \overline u }}{{\partial z}} + v'w'\frac{{\partial \overline v }}{{\partial z}} + w'w'\frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(13) |
|
$
{a_5} = - \left(\begin{array}{l}
u'\overline u \frac{{\partial \tilde u}}{{\partial x}} + v'\overline u \frac{{\partial \tilde v}}{{\partial x}} + w'\overline u \frac{{\partial \tilde w}}{{\partial x}} + u'\overline v \frac{{\partial \tilde u}}{{\partial y}} + v'\overline v \frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}w'\overline v \frac{{\partial \tilde w}}{{\partial y}} + u'\overline w \frac{{\partial \tilde u}}{{\partial z}} + v'\overline w \frac{{\partial \tilde v}}{{\partial z}} + w'\overline w \frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(14) |
|
$
{a_6} = - \left(\begin{array}{l}
\pi u'\tilde u\frac{{\partial \tilde u}}{{\partial x}} + v'\tilde u\frac{{\partial \tilde v}}{{\partial x}} + w'\tilde u\frac{{\partial \tilde w}}{{\partial x}} + u'\tilde v\frac{{\partial \tilde u}}{{\partial y}} + v'\tilde v\frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}w'\tilde v\frac{{\partial \tilde w}}{{\partial y}} + u'\tilde w\frac{{\partial \tilde u}}{{\partial z}} + v'\tilde w\frac{{\partial \tilde v}}{{\partial z}} + w'\tilde w\frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(15) |
|
$
{a_7} = - \left(\begin{array}{l}
u'u'\frac{{\partial \tilde u}}{{\partial x}} + v'u'\frac{{\partial \tilde v}}{{\partial x}} + w'u'\frac{{\partial \tilde w}}{{\partial x}} + u'v'\frac{{\partial \tilde u}}{{\partial y}} + v'v'\frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}w'v'\frac{{\partial \tilde w}}{{\partial y}} + u'w'\frac{{\partial \tilde u}}{{\partial z}} + v'w'\frac{{\partial \tilde v}}{{\partial z}} + w'w'\frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(16) |
|
$
{a_8} = - \left(\begin{array}{l}
u'\overline u \frac{{\partial u'}}{{\partial x}} + v'\overline u \frac{{\partial v'}}{{\partial x}} + w'\overline u \frac{{\partial w'}}{{\partial x}} + u'\overline v \frac{{\partial u'}}{{\partial y}} + v'\overline v \frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}w'\overline v \frac{{\partial w'}}{{\partial y}} + u'\overline w \frac{{\partial u'}}{{\partial z}} + v'\overline w \frac{{\partial v'}}{{\partial z}} + w'\overline w \frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(17) |
|
$
{a_9} = - \left(\begin{array}{l}
u'\tilde u\frac{{\partial u'}}{{\partial x}} + v'\tilde u\frac{{\partial v'}}{{\partial x}} + w'\tilde u\frac{{\partial w'}}{{\partial x}} + u'\tilde v\frac{{\partial u'}}{{\partial y}} + v'\tilde v\frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}w'\tilde v\frac{{\partial w'}}{{\partial y}} + u'\tilde w\frac{{\partial u'}}{{\partial z}} + v'\tilde w\frac{{\partial v'}}{{\partial z}} + w'\tilde w\frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(18) |
|
$
{a_{10}} = - \left(\begin{array}{l}
u'u'\frac{{\partial u'}}{{\partial x}} + v'u'\frac{{\partial v'}}{{\partial x}} + w'u'\frac{{\partial w'}}{{\partial x}} + u'v'\frac{{\partial u'}}{{\partial y}} + v'v'\frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}w'v'\frac{{\partial w'}}{{\partial y}} + u'w'\frac{{\partial u'}}{{\partial z}} + v'w'\frac{{\partial v'}}{{\partial z}} + w'w'\frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(19) |
|
$
{a_{11}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({u'\frac{{\partial \overline p }}{{\partial x}} + v'\frac{{\partial \overline p }}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({u'\frac{{\partial \overline p }}{{\partial x}} + v'\frac{{\partial \overline p }}{{\partial y}}} \right)} \right],
$
|
(20) |
|
$
{a_{12}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({u'\frac{{\partial \tilde p}}{{\partial x}} + v'\frac{{\partial \tilde p}}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({u'\frac{{\partial \tilde p}}{{\partial x}} + v'\frac{{\partial \tilde p}}{{\partial y}}} \right)} \right],
$
|
(21) |
|
$
\begin{array}{l}
{a_{13}} = \\
- \left[ {\frac{1}{{\overline \rho }} \cdot \left({u'\frac{{\partial p'}}{{\partial x}} + v'\frac{{\partial p'}}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({u'\frac{{\partial p'}}{{\partial x}} + v'\frac{{\partial p'}}{{\partial y}}} \right)} \right]
\end{array},
$
|
(22) |
|
$
{a_{14}} = - \left[ {w'\left({\frac{1}{{\overline \rho }} - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}}} \right)\frac{{\partial (\tilde p + p')}}{{\partial z}}} \right],
$
|
(23) |
|
$
{a_{15}} = \frac{g}{{\overline \theta }}w'\tilde \theta ,
$
|
(24) |
|
$
{a_{16}} = \frac{g}{{\overline \theta }}w'\theta ',
$
|
(25) |
|
$
{a_{17}} = - \left({w'\frac{{{c_v}}}{{{c_p}}}\frac{{\tilde p + p'}}{{\overline p }}g} \right),
$
|
(26) |
|
$
{a_{18}} = f(u'\overline v + u'\tilde v - \overline u v' - \tilde uv'),
$
|
(27) |
|
$
{a_{19}} = \upsilon \left[ \begin{array}{l}
u'\left({\frac{{{\partial ^2}\overline u }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline u }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline u }}{{\partial {z^2}}}} \right) + v'\left({\frac{{{\partial ^2}\overline v }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline v }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline v }}{{\partial {z^2}}}} \right) + \\
{\rm{ }}w'\left({\frac{{{\partial ^2}\overline w }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline w }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline w }}{{\partial {z^2}}}} \right)
\end{array} \right],
$
|
(28) |
|
$
{a_{20}} = \upsilon \left[ \begin{array}{l}
u'\left({\frac{{{\partial ^2}\tilde u}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde u}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde u}}{{\partial {z^2}}}} \right) + v'\left({\frac{{{\partial ^2}\tilde v}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde v}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde v}}{{\partial {z^2}}}} \right) + \\
{\rm{ }}w'\left({\frac{{{\partial ^2}\tilde w}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde w}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde w}}{{\partial {z^2}}}} \right)
\end{array} \right],
$
|
(29) |
|
$
{a_{21}} = \upsilon \left[ \begin{array}{l}
u'\left({\frac{{{\partial ^2}u'}}{{\partial {x^2}}} + \frac{{{\partial ^2}u'}}{{\partial {y^2}}} + \frac{{{\partial ^2}u'}}{{\partial {z^2}}}} \right) + v'\left({\frac{{{\partial ^2}v'}}{{\partial {x^2}}} + \frac{{{\partial ^2}v'}}{{\partial {y^2}}} + \frac{{{\partial ^2}v'}}{{\partial {z^2}}}} \right) + \\
{\rm{ }}w'\left({\frac{{{\partial ^2}w'}}{{\partial {x^2}}} + \frac{{{\partial ^2}w'}}{{\partial {y^2}}} + \frac{{{\partial ^2}w'}}{{\partial {z^2}}}} \right)
\end{array} \right],
$
|
(30) |
其中,各方程中等式左边的a1、a2、a3……、a21只是用以计数的量,没有其他含义(下同)。
进一步化简方程(9)得到:
|
$
\begin{array}{l}
\partial {K}'/\partial t= {I_\beta } + {T_K}_{\;(\beta, L)} + {T_K}_{\;(\beta, \alpha)} + {T_K}_{\;(\beta, \beta)} + {H_\beta } + {V_\beta } + \\
{B_{(\alpha, \beta)}} + {B_{(\beta, \beta)}} + {S_\beta } + {C_\beta } + {F_\beta }.
\end{array}
$
|
(31) |
公式(31)中各项的物理意义见表 1。
表 1(Table 1)
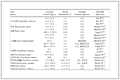
表 1 β中小尺度系统动能方程(31)中各项的物理意义
Table 1 Physical meanings of individual items in the meso-micro-β scale kinetic energy equation (31)
| 项 |
|
物理意义 |
| $\partial {K}'/\partial t$
|
|
β中小尺度系统动能变率项 |
| $ {I_\beta }$ |
${a_1} $ |
β中小尺度系统惯性力做功项 |
| $ {T_K}_{\;\left({\beta, L} \right)}$ |
$ {a_2} + {a_3} + {a_4} = - V'[(\overline V + \tilde V + V') \cdot {\nabla _3}]\overline V $ |
大尺度背景场向β中小尺度系统的动能转换项 |
| ${T_K}_{\;\left({\beta, \alpha } \right)} $ |
${a_5} + {a_6} + {a_7} = - V'[(\overline V + \tilde V + V') \cdot {\nabla _3}]\tilde V $ |
α中尺度系统向β中小尺度系统的动能转换项 |
| ${T_K}_{\;(\beta, \beta)} $ |
${a_8} + {a_9} + {a_{10}} = - V'[(\overline V + \tilde V + V') \cdot {\nabla _3}]V' $ |
β中小尺度系统动能输送项 |
| ${H_\beta } $ |
${a_{11}} + {a_{12}} + {a_{13}} $ |
β中小尺度系统水平气压梯度力做功项 |
| ${V_\beta } $ |
$ {a_{14}}$ |
垂直方向扰动气压梯度力在β中小尺度系统垂直气流中的做功项 |
| $ {B_{(\alpha, \beta)}}$ |
${a_{15}} $ |
α中尺度系统气团受到的浮力在β中小尺度系统垂直气流中的做功项 |
| ${B_{(\beta, \beta)}} $ |
${a_{16}} $ |
β中小尺度气团受到的浮力在β中小尺度系统垂直气流中的做功项 |
| ${S_\beta } $ |
$ {a_{17}}$ |
空气的压缩效应 |
| ${C_\beta } $ |
${a_{18}} $ |
β中小尺度系统地转偏向力做功项 |
| ${F_\beta } $ |
${a_{19}} + {a_{20}} + {a_{21}} $ |
β中小尺度系统摩擦力做功项 |
|
表 1 β中小尺度系统动能方程(31)中各项的物理意义
Table 1 Physical meanings of individual items in the meso-micro-β scale kinetic energy equation (31)
|
2.2.2 计算$ \tilde{u}\times 公式(1)+\tilde{v}\times 公式(2)+\tilde{w}\times 公式(8)$,求${\partial \tilde{K}}/{\partial \ t}\; $
|
$
\begin{array}{l}
\partial \tilde{K}\text{/}\partial \ t = {b_1} + {b_2} + {b_3} + {b_4} + {b_5} + {b_6} + {b_7} + {b_8} + {b_9} + {b_{10}} + {b_{11}} + \\
{b_{12}} + {b_{13}} + {b_{14}} + {b_{15}} + {b_{16}} + {b_{17}} + {b_{18}} + {b_{19}} + {b_{20}} + {b_{21}},
\end{array}
$
|
(32) |
|
$
{b_1} = - \left[ {\tilde u(\frac{{\partial \overline u }}{{\partial t}} + \frac{{\partial u'}}{{\partial t}}) + \tilde v(\frac{{\partial \overline v }}{{\partial t}} + \frac{{\partial v'}}{{\partial t}}) + \tilde w(\frac{{\partial \overline w }}{{\partial t}} + \frac{{\partial w'}}{{\partial t}})} \right],
$
|
(33) |
|
$
{b_2} = - \left(\begin{array}{l}
\tilde u\overline u \frac{{\partial \overline u }}{{\partial x}} + \tilde v\overline u \frac{{\partial \overline v }}{{\partial x}} + \tilde w\overline u \frac{{\partial \overline w }}{{\partial x}} + \tilde u\overline v \frac{{\partial \overline u }}{{\partial y}} + \tilde v\overline v \frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}\tilde w\overline v \frac{{\partial \overline w }}{{\partial y}} + \tilde u\overline w \frac{{\partial \overline u }}{{\partial z}} + \tilde v\overline w \frac{{\partial \overline v }}{{\partial z}} + \tilde w\overline w \frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(34) |
|
$
{b_3} = - \left(\begin{array}{l}
\tilde u\tilde u\frac{{\partial \overline u }}{{\partial x}} + \tilde v\tilde u\frac{{\partial \overline v }}{{\partial x}} + \tilde w\tilde u\frac{{\partial \overline w }}{{\partial x}} + \tilde u\tilde v\frac{{\partial \overline u }}{{\partial y}} + \tilde v\tilde v\frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}\tilde w\tilde v\frac{{\partial \overline w }}{{\partial y}} + \tilde u\tilde w\frac{{\partial \overline u }}{{\partial z}} + \tilde v\tilde w\frac{{\partial \overline v }}{{\partial z}} + \tilde w\tilde w\frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(35) |
|
$
{b_4} = - \left(\begin{array}{l}
\tilde uu'\frac{{\partial \overline u }}{{\partial x}} + \tilde vu'\frac{{\partial \overline v }}{{\partial x}} + \tilde wu'\frac{{\partial \overline w }}{{\partial x}} + \tilde uv'\frac{{\partial \overline u }}{{\partial y}} + \tilde vv'\frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}\tilde wv'\frac{{\partial \overline w }}{{\partial y}} + \tilde uw'\frac{{\partial \overline u }}{{\partial z}} + \tilde vw'\frac{{\partial \overline v }}{{\partial z}} + \tilde ww'\frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(36) |
|
$
{b_5} = - \left(\begin{array}{l}
\tilde u\overline u \frac{{\partial \tilde u}}{{\partial x}} + \tilde v\overline u \frac{{\partial \tilde v}}{{\partial x}} + \tilde w\overline u \frac{{\partial \tilde w}}{{\partial x}} + \tilde u\overline v \frac{{\partial \tilde u}}{{\partial y}} + \tilde v\overline v \frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}\tilde w\overline v \frac{{\partial \tilde w}}{{\partial y}} + \tilde u\overline w \frac{{\partial \tilde u}}{{\partial z}} + \tilde v\overline w \frac{{\partial \tilde v}}{{\partial z}} + \tilde w\overline w \frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(37) |
|
$
{b_6} = - \left(\begin{array}{l}
\tilde u\tilde u\frac{{\partial \tilde u}}{{\partial x}} + \tilde v\tilde u\frac{{\partial \tilde v}}{{\partial x}} + \tilde w\tilde u\frac{{\partial \tilde w}}{{\partial x}} + \tilde u\tilde v\frac{{\partial \tilde u}}{{\partial y}} + \tilde v\tilde v\frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}\tilde w\tilde v\frac{{\partial \tilde w}}{{\partial y}} + \tilde u\tilde w\frac{{\partial \tilde u}}{{\partial z}} + \tilde v\tilde w\frac{{\partial \tilde v}}{{\partial z}} + \tilde w\tilde w\frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(38) |
|
$
{b_7} = - \left(\begin{array}{l}
\tilde uu'\frac{{\partial \tilde u}}{{\partial x}} + \tilde vu'\frac{{\partial \tilde v}}{{\partial x}} + \tilde wu'\frac{{\partial \tilde w}}{{\partial x}} + \tilde uv'\frac{{\partial \tilde u}}{{\partial y}} + \tilde vv'\frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}\tilde wv'\frac{{\partial \tilde w}}{{\partial y}} + \tilde uw'\frac{{\partial \tilde u}}{{\partial z}} + \tilde vw'\frac{{\partial \tilde v}}{{\partial z}} + \tilde ww'\frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(39) |
|
$
{b_8} = - \left(\begin{array}{l}
\tilde u\overline u \frac{{\partial u'}}{{\partial x}} + \tilde v\overline u \frac{{\partial v'}}{{\partial x}} + \tilde w\overline u \frac{{\partial w'}}{{\partial x}} + \tilde u\overline v \frac{{\partial u'}}{{\partial y}} + \tilde v\overline v \frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}\tilde w\overline v \frac{{\partial w'}}{{\partial y}} + \tilde u\overline w \frac{{\partial u'}}{{\partial z}} + \tilde v\overline w \frac{{\partial v'}}{{\partial z}} + \tilde w\overline w \frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(40) |
|
$
{b_9} = - \left(\begin{array}{l}
\tilde u\tilde u\frac{{\partial u'}}{{\partial x}} + \tilde v\tilde u\frac{{\partial v'}}{{\partial x}} + \tilde w\tilde u\frac{{\partial w'}}{{\partial x}} + \tilde u\tilde v\frac{{\partial u'}}{{\partial y}} + \tilde v\tilde v\frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}\tilde w\tilde v\frac{{\partial w'}}{{\partial y}} + \tilde u\tilde w\frac{{\partial u'}}{{\partial z}} + \tilde v\tilde w\frac{{\partial v'}}{{\partial z}} + \tilde w\tilde w\frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(41) |
|
$
{b_{10}} = - \left(\begin{array}{l}
\tilde uu'\frac{{\partial u'}}{{\partial x}} + \tilde vu'\frac{{\partial v'}}{{\partial x}} + \tilde wu'\frac{{\partial w'}}{{\partial x}} + \tilde uv'\frac{{\partial u'}}{{\partial y}} + \tilde vv'\frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}\tilde wv'\frac{{\partial w'}}{{\partial y}} + \tilde uw'\frac{{\partial u'}}{{\partial z}} + \tilde vw'\frac{{\partial v'}}{{\partial z}} + \tilde ww'\frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(42) |
|
$
{b_{11}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({\tilde u\frac{{\partial \overline p }}{{\partial x}} + \tilde v\frac{{\partial \overline p }}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({\tilde u\frac{{\partial \overline p }}{{\partial x}} + \tilde v\frac{{\partial \overline p }}{{\partial y}}} \right)} \right],
$
|
(43) |
|
$
{b_{12}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({\tilde u\frac{{\partial \tilde p}}{{\partial x}} + \tilde v\frac{{\partial \tilde p}}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({\tilde u\frac{{\partial \tilde p}}{{\partial x}} + \tilde v\frac{{\partial \tilde p}}{{\partial y}}} \right)} \right],
$
|
(44) |
|
$
{b_{13}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({\tilde u\frac{{\partial p'}}{{\partial x}} + \tilde v\frac{{\partial p'}}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({\tilde u\frac{{\partial p'}}{{\partial x}} + \tilde v\frac{{\partial p'}}{{\partial y}}} \right)} \right],
$
|
(45) |
|
$
{b_{14}} = - \left[ {\tilde w\left({\frac{1}{{\overline \rho }} - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}}} \right)\frac{{\partial (\tilde p + p')}}{{\partial z}}} \right],
$
|
(46) |
|
$
{b_{15}} = \frac{g}{{\overline \theta }}\tilde w\tilde \theta ,
$
|
(47) |
|
$
{b_{16}} = \frac{g}{{\overline \theta }}\tilde w\theta ',
$
|
(48) |
|
$
{b_{17}} = - \left({\tilde w\frac{{{c_v}}}{{{c_p}}}\frac{{\tilde p + p'}}{{\overline p }}g} \right),
$
|
(49) |
|
$
{b_{18}} = f(\tilde u\overline v + \tilde u\tilde v - \overline u \tilde v - \tilde u\tilde v),
$
|
(50) |
|
$
{b_{19}} = \upsilon \left[ \begin{array}{l}
\tilde u\left({\frac{{{\partial ^2}\overline u }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline u }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline u }}{{\partial {z^2}}}} \right) + \tilde v\left({\frac{{{\partial ^2}\overline v }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline v }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline v }}{{\partial {z^2}}}} \right) + \\
{\rm{ }}\tilde w\left({\frac{{{\partial ^2}\overline w }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline w }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline w }}{{\partial {z^2}}}} \right)
\end{array} \right],
$
|
(51) |
|
$
{b_{20}} = \upsilon \left[ \begin{array}{l}
\tilde u\left({\frac{{{\partial ^2}\tilde u}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde u}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde u}}{{\partial {z^2}}}} \right) + \tilde v\left({\frac{{{\partial ^2}\tilde v}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde v}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde v}}{{\partial {z^2}}}} \right) + \\
{\rm{ }}\tilde w\left({\frac{{{\partial ^2}\tilde w}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde w}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde w}}{{\partial {z^2}}}} \right)
\end{array} \right],
$
|
(52) |
|
$
{b_{21}} = \upsilon \left[ \begin{array}{l}
\tilde u\left({\frac{{{\partial ^2}u'}}{{\partial {x^2}}} + \frac{{{\partial ^2}u'}}{{\partial {y^2}}} + \frac{{{\partial ^2}u'}}{{\partial {z^2}}}} \right) + \tilde v\left({\frac{{{\partial ^2}v'}}{{\partial {x^2}}} + \frac{{{\partial ^2}v'}}{{\partial {y^2}}} + \frac{{{\partial ^2}v'}}{{\partial {z^2}}}} \right) + \\
\tilde w\left({\frac{{{\partial ^2}w'}}{{\partial {x^2}}} + \frac{{{\partial ^2}w'}}{{\partial {y^2}}} + \frac{{{\partial ^2}w'}}{{\partial {z^2}}}} \right)
\end{array} \right].
$
|
(53) |
进一步化简方程(32),得到:
|
$
\begin{array}{l}
\partial \tilde{K}\text{/}\partial \ t = {I_\alpha } + {T_K}_{\;(\alpha, L)} + {T_K}_{\;(\alpha, \alpha)} + {T_K}_{\;(\alpha, \beta)} + {H_\alpha } + \\
{V_\alpha } + {B_{(\alpha, \alpha)}} + {B_{(\beta, \alpha)}} + {S_\alpha } + {C_\alpha } + {F_\alpha }.
\end{array}
$
|
(54) |
公式(54)中各项的物理意义见表 2。
表 2(Table 2)

表 2 α中尺度系统动能方程(54)中各项的物理意义
Table 2 Physical meanings of individual items in the meso-α scale kinetic energy equation (54)
| 项 |
|
物理意义 |
| $\partial \tilde{K}\text{/}\partial \ t $
|
|
α中尺度系统动能变率项 |
| $ {I_\alpha }$ |
$ {b_1}$ |
α中尺度系统惯性力做功项 |
| ${T_K}_{\;\left({\alpha, L} \right)} $ |
${b_2} + {b_3} + {b_4} = - \tilde V[(\overline V + \tilde V + V') \cdot {\nabla _3}]\overline V $ |
大尺度背景场向α中尺度系统的动能转换项 |
| ${T_K}_{\;(\alpha, \alpha)} $ |
$ {b_5} + {b_6} + {b_7} = - \tilde V[(\overline V + \tilde V + V') \cdot {\nabla _3}]\tilde V$ |
α中尺度系统动能输送项 |
| ${T_K}_{\;\left({\alpha, \beta } \right)} $ |
${b_8} + {b_9} + {b_{10}} = - \tilde V[(\overline V + \tilde V + V') \cdot {\nabla _3}]V' $ |
β中小尺度系统向α中尺度系统的动能转换项 |
| ${H_\alpha } $ |
${b_{11}} + {b_{12}} + {b_{13}} $ |
α中尺度系统水平气压梯度力做功项 |
| ${V_\alpha } $ |
${b_{14}} $ |
垂直方向扰动气压梯度力在α中尺度系统垂直气流中的做功项 |
| ${B_{(\alpha, \alpha)}} $ |
$ {b_{15}}$ |
α中尺度系统气团受到的浮力在α中尺度系统垂直气流中的做功项 |
| $ {B_{(\beta, \alpha)}}$ |
${b_{16}} $ |
β中小尺度系统气团受到的浮力在α中尺度系统垂直气流中的做功项 |
| $ {S_\alpha }$ |
$ {b_{17}}$ |
空气的压缩效应 |
| $ {C_\alpha }$ |
${b_{18}} $ |
α中尺度系统地转偏向力做功项 |
| ${F_\alpha } $ |
${b_{19}} + {b_{20}} + {b_{21}} $ |
α中尺度系统摩擦力做功项 |
|
表 2 α中尺度系统动能方程(54)中各项的物理意义
Table 2 Physical meanings of individual items in the meso-α scale kinetic energy equation (54)
|
2.2.3 计算$ \overline{u}\times 公式(1)+\overline{v}\times 公式(2)+\overline{w}\times 公式(8)$,求${\partial \overline{K}}/{\partial \ t}\; $
|
$
\begin{array}{l}
\partial \tilde{K}\text{/}\partial \ t = {c_1} + {c_2} + {c_3} + {c_4} + {c_5} + {c_6} + {c_7} + {c_8} + {c_9} + {c_{10}} + \\
{c_{11}} + {c_{12}} + {c_{13}} + {c_{14}} + {c_{15}} + {c_{16}} + {c_{17}} + {c_{18}} + {c_{19}} + {c_{20}} + {c_{21}},
\end{array}
$
|
(55) |
|
$
{c_1} = - \left[ {\overline u (\frac{{\partial \tilde u}}{{\partial t}} + \frac{{\partial u'}}{{\partial t}}) + \overline v (\frac{{\partial \tilde v}}{{\partial t}} + \frac{{\partial v'}}{{\partial t}}) + \overline w (\frac{{\partial \tilde w}}{{\partial t}} + \frac{{\partial w'}}{{\partial t}})} \right],
$
|
(56) |
|
$
{c_2} = - \left(\begin{array}{l}
\overline u \overline u \frac{{\partial \overline u }}{{\partial x}} + \overline v \overline u \frac{{\partial \overline v }}{{\partial x}} + \overline w \overline u \frac{{\partial \overline w }}{{\partial x}} + \overline u \overline v \frac{{\partial \overline u }}{{\partial y}} + \overline v \overline v \frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}\overline w \overline v \frac{{\partial \overline w }}{{\partial y}} + \overline u \overline w \frac{{\partial \overline u }}{{\partial z}} + \overline v \overline w \frac{{\partial \overline v }}{{\partial z}} + \overline w \overline w \frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(57) |
|
$
{c_3} = - \left(\begin{array}{l}
\overline u \tilde u\frac{{\partial \overline u }}{{\partial x}} + \overline v \tilde u\frac{{\partial \overline v }}{{\partial x}} + \overline w \tilde u\frac{{\partial \overline w }}{{\partial x}} + \overline u \tilde v\frac{{\partial \overline u }}{{\partial y}} + \overline v \tilde v\frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}\overline w \tilde v\frac{{\partial \overline w }}{{\partial y}} + \overline u \tilde w\frac{{\partial \overline u }}{{\partial z}} + \overline v \tilde w\frac{{\partial \overline v }}{{\partial z}} + \overline w \tilde w\frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(58) |
|
$
{c_4} = - \left(\begin{array}{l}
\overline u u'\frac{{\partial \overline u }}{{\partial x}} + \overline v u'\frac{{\partial \overline v }}{{\partial x}} + \overline w u'\frac{{\partial \overline w }}{{\partial x}} + \overline u v'\frac{{\partial \overline u }}{{\partial y}} + \overline v v'\frac{{\partial \overline v }}{{\partial y}} + \\
{\rm{ }}\overline w v'\frac{{\partial \overline w }}{{\partial y}} + \overline u w'\frac{{\partial \overline u }}{{\partial z}} + \overline v w'\frac{{\partial \overline v }}{{\partial z}} + \overline w w'\frac{{\partial \overline w }}{{\partial z}}
\end{array} \right),
$
|
(59) |
|
$
{c_5} = - \left(\begin{array}{l}
\overline u \overline u \frac{{\partial \tilde u}}{{\partial x}} + \overline v \overline u \frac{{\partial \tilde v}}{{\partial x}} + \overline w \overline u \frac{{\partial \tilde w}}{{\partial x}} + \overline u \overline v \frac{{\partial \tilde u}}{{\partial y}} + \overline v \overline v \frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}\overline w \overline v \frac{{\partial \tilde w}}{{\partial y}} + \overline u \overline w \frac{{\partial \tilde u}}{{\partial z}} + \overline v \overline w \frac{{\partial \tilde v}}{{\partial z}} + \overline w \overline w \frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(60) |
|
$
{c_6} = - \left(\begin{array}{l}
\overline u \tilde u\frac{{\partial \tilde u}}{{\partial x}} + \overline v \tilde u\frac{{\partial \tilde v}}{{\partial x}} + \overline w \tilde u\frac{{\partial \tilde w}}{{\partial x}} + \overline u \tilde v\frac{{\partial \tilde u}}{{\partial y}} + \overline v \tilde v\frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}\overline w \tilde v\frac{{\partial \tilde w}}{{\partial y}} + \overline u \tilde w\frac{{\partial \tilde u}}{{\partial z}} + \overline v \tilde w\frac{{\partial \tilde v}}{{\partial z}} + \overline w \tilde w\frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(61) |
|
$
{c_7} = - \left(\begin{array}{l}
\overline u u'\frac{{\partial \tilde u}}{{\partial x}} + \overline v u'\frac{{\partial \tilde v}}{{\partial x}} + \overline w u'\frac{{\partial \tilde w}}{{\partial x}} + \overline u v'\frac{{\partial \tilde u}}{{\partial y}} + \overline v v'\frac{{\partial \tilde v}}{{\partial y}} + \\
{\rm{ }}\overline w v'\frac{{\partial \tilde w}}{{\partial y}} + \overline u w'\frac{{\partial \tilde u}}{{\partial z}} + \overline v w'\frac{{\partial \tilde v}}{{\partial z}} + \overline w w'\frac{{\partial \tilde w}}{{\partial z}}
\end{array} \right),
$
|
(62) |
|
$
{c_8} = - \left(\begin{array}{l}
\overline u \overline u \frac{{\partial u'}}{{\partial x}} + \overline v \overline u \frac{{\partial v'}}{{\partial x}} + \overline w \overline u \frac{{\partial w'}}{{\partial x}} + \overline u \overline v \frac{{\partial u'}}{{\partial y}} + \overline v \overline v \frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}\overline w \overline v \frac{{\partial w'}}{{\partial y}} + \overline u \overline w \frac{{\partial u'}}{{\partial z}} + \overline v \overline w \frac{{\partial v'}}{{\partial z}} + \overline w \overline w \frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(63) |
|
$
{c_9} = - \left(\begin{array}{l}
\overline u \tilde u\frac{{\partial u'}}{{\partial x}} + \overline v \tilde u\frac{{\partial v'}}{{\partial x}} + \overline w \tilde u\frac{{\partial w'}}{{\partial x}} + \overline u \tilde v\frac{{\partial u'}}{{\partial y}} + \overline v \tilde v\frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}\overline w \tilde v\frac{{\partial w'}}{{\partial y}} + \overline u \tilde w\frac{{\partial u'}}{{\partial z}} + \overline v \tilde w\frac{{\partial v'}}{{\partial z}} + \overline w \tilde w\frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(64) |
|
$
{c_{10}} = - \left(\begin{array}{l}
\overline u u'\frac{{\partial u'}}{{\partial x}} + \overline v u'\frac{{\partial v'}}{{\partial x}} + \overline w u'\frac{{\partial w'}}{{\partial x}} + \overline u v'\frac{{\partial u'}}{{\partial y}} + \overline v v'\frac{{\partial v'}}{{\partial y}} + \\
{\rm{ }}\overline w v'\frac{{\partial w'}}{{\partial y}} + \overline u w'\frac{{\partial u'}}{{\partial z}} + \overline v w'\frac{{\partial v'}}{{\partial z}} + \overline w w'\frac{{\partial w'}}{{\partial z}}
\end{array} \right),
$
|
(65) |
|
$
{c_{11}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({\overline u \frac{{\partial \overline p }}{{\partial x}} + \overline v \frac{{\partial \overline p }}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({\overline u \frac{{\partial \overline p }}{{\partial x}} + \overline v \frac{{\partial \overline p }}{{\partial y}}} \right)} \right],
$
|
(66) |
|
$
{c_{12}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({\overline u \frac{{\partial \tilde p}}{{\partial x}} + \overline v \frac{{\partial \tilde p}}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({\overline u \frac{{\partial \tilde p}}{{\partial x}} + \overline v \frac{{\partial \tilde p}}{{\partial y}}} \right)} \right],
$
|
(67) |
|
$
{c_{13}} = - \left[ {\frac{1}{{\overline \rho }} \cdot \left({\overline u \frac{{\partial p'}}{{\partial x}} + \overline v \frac{{\partial p'}}{{\partial y}}} \right) - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}} \cdot \left({\overline u \frac{{\partial p'}}{{\partial x}} + \overline v \frac{{\partial p'}}{{\partial y}}} \right)} \right],
$
|
(68) |
|
$
{c_{14}} = - \left[ {\overline w \left({\frac{1}{{\overline \rho }} - \frac{{\tilde \rho + \rho '}}{{{{\overline \rho }^2}}}} \right)\frac{{\partial (\tilde p + p')}}{{\partial z}}} \right],
$
|
(69) |
|
$
{c_{15}} = \frac{g}{{\overline \theta }}\overline w \tilde \theta ,
$
|
(70) |
|
$
{c_{16}} = \frac{g}{{\overline \theta }}\overline w \theta ',
$
|
(71) |
|
$
{c_{17}} = - \left({\overline w \frac{{{c_v}}}{{{c_p}}}\frac{{\tilde p + p'}}{{\overline p }}g} \right),
$
|
(72) |
|
$
{c_{18}} = f(\overline u \overline v + \overline u \tilde v - \overline u \overline v - \tilde u\overline v),
$
|
(73) |
|
$
{c_{19}} = \upsilon \left[ \begin{array}{l}
\overline u \left({\frac{{{\partial ^2}\overline u }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline u }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline u }}{{\partial {z^2}}}} \right) + \overline v \left({\frac{{{\partial ^2}\overline v }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline v }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline v }}{{\partial {z^2}}}} \right) + \\
{\rm{ }}\overline w \left({\frac{{{\partial ^2}\overline w }}{{\partial {x^2}}} + \frac{{{\partial ^2}\overline w }}{{\partial {y^2}}} + \frac{{{\partial ^2}\overline w }}{{\partial {z^2}}}} \right)
\end{array} \right],
$
|
(74) |
|
$
{c_{20}} = \upsilon \left[ \begin{array}{l}
\overline u \left({\frac{{{\partial ^2}\tilde u}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde u}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde u}}{{\partial {z^2}}}} \right) + \overline v \left({\frac{{{\partial ^2}\tilde v}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde v}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde v}}{{\partial {z^2}}}} \right) + \\
{\rm{ }}\overline w \left({\frac{{{\partial ^2}\tilde w}}{{\partial {x^2}}} + \frac{{{\partial ^2}\tilde w}}{{\partial {y^2}}} + \frac{{{\partial ^2}\tilde w}}{{\partial {z^2}}}} \right)
\end{array} \right],
$
|
(75) |
|
$
{c_{21}} = \upsilon \left[ \begin{array}{l}
\overline u \left({\frac{{{\partial ^2}u'}}{{\partial {x^2}}} + \frac{{{\partial ^2}u'}}{{\partial {y^2}}} + \frac{{{\partial ^2}u'}}{{\partial {z^2}}}} \right) + \overline v \left({\frac{{{\partial ^2}v'}}{{\partial {x^2}}} + \frac{{{\partial ^2}v'}}{{\partial {y^2}}} + \frac{{{\partial ^2}v'}}{{\partial {z^2}}}} \right) + \\
{\rm{ }}\overline w \left({\frac{{{\partial ^2}w'}}{{\partial {x^2}}} + \frac{{{\partial ^2}w'}}{{\partial {y^2}}} + \frac{{{\partial ^2}w'}}{{\partial {z^2}}}} \right)
\end{array} \right].
$
|
(76) |
进一步化简方程(55),得到:
|
$
\begin{array}{l}
\partial \bar{K}/\partial t= {I_L} + {T_K}_{\;(L, L)} + {T_K}_{\;(L, \alpha)} + {T_K}_{\;(L, \beta)} + {H_L} + \\
{V_L} + {B_{(\alpha, L)}} + {B_{(\beta, L)}} + {S_L} + {C_L} + {F_L}.
\end{array}
$
|
(77) |
公式(77)中各项的物理意义见表 3。
表 3(Table 3)

表 3 大尺度背景场动能方程(77)中各项的物理意义
Table 3 Physical meanings of individual items in the large scale background field kinetic energy equation (77)
| 项 |
|
物理意义 |
| $\partial \bar{K}/\partial t$
|
|
大尺度背景场动能变率项 |
| ${I_L} $ |
$ {c_1}$ |
大尺度背景场惯性力做功项 |
| $ {T_K}_{\;(L, L)}$ |
$ {c_2} + {c_3} + {c_4} = - \overline V [(\overline V + \tilde V + V') \cdot {\nabla _3}]\overline V $ |
大尺度背景场动能输送项 |
| $ {T_K}_{\;\left({L, \alpha } \right)}$ |
${c_5} + {c_6} + {c_7} = - \overline V [(\overline V + \tilde V + V') \cdot {\nabla _3}]\tilde V $ |
α中尺度系统向大尺度背景场的动能转换项 |
| $ {T_K}_{\;\left({L, \beta } \right)}$ |
$ {c_8} + {c_9} + {c_{10}} = - \overline V [(\overline V + \tilde V + V') \cdot {\nabla _3}]V'$ |
β中小尺度系统向大尺度背景场的动能转换项 |
| ${H_L} $ |
${c_{11}} + {c_{12}} + {c_{13}} $ |
大尺度背景场水平气压梯度力做功项 |
| $ {V_L}$ |
${c_{14}} $ |
垂直方向扰动气压梯度力在大尺度背景场垂直气流中的做功项 |
| $ {B_{(\alpha, L)}}$ |
${c_{15}} $ |
α中尺度系统气团受到的浮力在大尺度背景场垂直气流中的做功项 |
| ${B_{(\beta, L)}} $ |
${c_{16}} $ |
β中小尺度系统气团受到的浮力在大尺度背景场垂直气流中的做功项 |
| ${S_L} $ |
$ {c_{17}}$ |
空气的压缩效应 |
| ${C_L} $ |
$ {c_{18}}$ |
大尺度背景场地转偏向力做功项 |
| $ {F_L}$ |
${c_{19}} + {c_{20}} + {c_{21}} $ |
大尺度背景场摩擦力做功项 |
|
表 3 大尺度背景场动能方程(77)中各项的物理意义
Table 3 Physical meanings of individual items in the large scale background field kinetic energy equation (77)
|
2.3 位能方程的推导
2.3.1 计算$ {\theta }'\times 公式(4)$,求${\partial {A}'}/{\partial \ t}\; $
|
$
\begin{array}{l}
\partial {A}'/\partial \ t= \frac{\partial }{{\partial \;t}}\left({\frac{\gamma }{2}{{\theta '}^2}} \right) = {d_1} + {d_2} + {d_3} + {d_4} + \\
{d_5} + {d_6} + {d_7} + {d_8},
\end{array}
$
|
(78) |
|
$
{d_1} = - \left[ {\gamma \;\theta '\frac{{\partial \left({\overline \theta + \tilde \theta } \right)}}{{\partial t}}} \right],
$
|
(79) |
|
$
{d_2} = - \gamma \left(\begin{array}{l}
\theta '\;\overline u \frac{{\partial \overline \theta }}{{\partial x}}\; + \theta '\;\overline v \frac{{\partial \overline \theta }}{{\partial y}} + \theta '\;\tilde u\frac{{\partial \overline \theta }}{{\partial x}} + \\
{\rm{ }}\theta '\;\tilde v\frac{{\partial \overline \theta }}{{\partial y}} + \theta '\;u'\frac{{\partial \overline \theta }}{{\partial x}} + \theta '\;v'\frac{{\partial \overline \theta }}{{\partial y}}
\end{array} \right),
$
|
(80) |
|
$
{d_3} = - \gamma \left(\begin{array}{l}
\theta '\;\overline u \frac{{\partial \tilde \theta }}{{\partial x}}\; + \theta '\;\overline v \frac{{\partial \tilde \theta }}{{\partial y}} + \theta '\;\tilde u\frac{{\partial \tilde \theta }}{{\partial x}} + \\
{\rm{ }}\theta '\;\tilde v\frac{{\partial \tilde \theta }}{{\partial y}} + \theta '\;u'\frac{{\partial \tilde \theta }}{{\partial x}} + \theta '\;v'\frac{{\partial \tilde \theta }}{{\partial y}}
\end{array} \right),
$
|
(81) |
|
$
{d_4} = - \gamma \left(\begin{array}{l}
\theta '\;\overline u \frac{{\partial \theta '}}{{\partial x}}\; + \theta '\;\overline v \frac{{\partial \theta '}}{{\partial y}} + \theta '\;\tilde u\frac{{\partial \theta '}}{{\partial x}} + \\
{\rm{ }}\theta '\;\tilde v\frac{{\partial \theta '}}{{\partial y}} + \theta '\;u'\frac{{\partial \theta '}}{{\partial x}} + \theta '\;v'\frac{{\partial \theta '}}{{\partial y}}
\end{array} \right),
$
|
(82) |
|
$
{d_5} = - \left({\frac{{\theta '}}{{\overline \theta }}\overline w g} \right),
$
|
(83) |
|
$
{d_6} = - \left({\frac{{\theta '}}{{\overline \theta }}\tilde wg} \right),
$
|
(84) |
|
$
{d_7} = - \left({\frac{{\theta '}}{{\overline \theta }}w'g} \right),
$
|
(85) |
|
$
{d_8} = \gamma \frac{{\theta '}}{{{c_p}}}{\left({\frac{p}{{{p_0}}}} \right)^{R/{{c}_{p}}}}\left({\overline Q + \tilde Q + Q'} \right),
$
|
(86) |
其中,系数$ \gamma =\left({}^{g}\!\!\diagup\!\!{}_{\overline{\theta }}\; \right){{\left({}^{\partial \theta }\!\!\diagup\!\!{}_{\partial z}\; \right)}^{-1}}$。
进一步化简方程(78),得到:
|
$
\begin{array}{l}
\partial {A}'/\partial \ t= \frac{\partial }{{\partial \;t}}\left({\frac{\gamma }{2}{{\theta '}^2}} \right) = {P_{\;\beta }} + {T_P}_{\;(\beta, L)} + {T_P}_{\;(\beta, \alpha)} + \\
{T_P}_{\;(\beta, \beta)} - {B_{(\beta, L)}} - {B_{(\beta, \alpha)}} - {B_{(\beta, \beta)}} + {D_\beta }.
\end{array}
$
|
(87) |
公式(87)中各项的物理意义见表 4。
表 4(Table 4)

表 4 β中小尺度系统位能方程(87)中各项的物理意义
Table 4 Physical meanings of individual items in the meso- micro-β scale potential energy equation (87)
| 项 |
|
物理意义 |
| $\partial {A}'/\partial \ t$ |
|
β中小尺度系统位能变率 |
| ${P_{\;\beta }} $ |
$ {d_1}$ |
β中小尺度系统与大尺度背景场和α中尺度系统位能之间的相互作用 |
| ${T_P}_{\;(\beta, L)} $ |
${d_2} $ |
大尺度背景场向β中小尺度系统的位能转换项 |
| $ {T_P}_{\;(\beta, \alpha)}$ |
${d_3} $ |
α中尺度系统向β中小尺度系统的位能转换项 |
| $ {T_P}_{\;(\beta, \beta)}$ |
$ {d_4}$ |
β中小尺度系统位能的水平输送 |
| $ {B_{\;(\beta, L)}}$ |
${d_5} $ |
β中小尺度系统气团受到的浮力在大尺度背景场垂直气流中的做功项 |
| ${B_{(\beta, \alpha)}} $ |
$ {d_6}$ |
β中小尺度系统气团受到的浮力在α中尺度系统垂直气流中的做功项 |
| ${B_{(\beta, \beta)}} $ |
$ {d_7}$ |
β中小尺度系统气团受到的浮力在β中小尺度系统垂直气流中的做功项 |
| ${D_\beta } $ |
$ {d_8}$
|
β中小尺度系统非绝热加热做功 |
|
表 4 β中小尺度系统位能方程(87)中各项的物理意义
Table 4 Physical meanings of individual items in the meso- micro-β scale potential energy equation (87)
|
2.3.2 计算$\tilde{\theta }\times 公式(4) $,求$ {\partial \tilde{A}}/{\partial \ t}\;$
|
$
\partial \tilde{A}/\partial \ t= \frac{\partial }{{\partial \;t}}\left({\frac{\gamma }{2}{{\tilde \theta }^2}} \right) = {e_1} + {e_2} + {e_3} + {e_4} + {e_5} + {e_6} + {e_7} + {e_8},
$
|
(88) |
|
$
{e_1} = - \left[ {\gamma \;\tilde \theta \frac{{\partial \left({\overline \theta + \theta '} \right)}}{{\partial t}}} \right],
$
|
(89) |
|
$
{e_2} = - \gamma \left(\begin{array}{l}
\tilde \theta \;\overline u \frac{{\partial \overline \theta }}{{\partial x}}\; + \tilde \theta \;\overline v \frac{{\partial \overline \theta }}{{\partial y}} + \tilde \theta \;\tilde u\frac{{\partial \overline \theta }}{{\partial x}} + \tilde \theta \;\tilde v\frac{{\partial \overline \theta }}{{\partial y}} + \\
{\rm{ }}\tilde \theta \;u'\frac{{\partial \overline \theta }}{{\partial x}} + \tilde \theta \;v'\frac{{\partial \overline \theta }}{{\partial y}}
\end{array} \right),
$
|
(90) |
|
$
{e_3} = - \gamma \left(\begin{array}{l}
\tilde \theta \;\overline u \frac{{\partial \tilde \theta }}{{\partial x}}\; + \tilde \theta \;\overline v \frac{{\partial \tilde \theta }}{{\partial y}} + \tilde \theta \;\tilde u\frac{{\partial \tilde \theta }}{{\partial x}} + \tilde \theta \;\tilde v\frac{{\partial \tilde \theta }}{{\partial y}} + \\
{\rm{ }}\tilde \theta \;u'\frac{{\partial \tilde \theta }}{{\partial x}} + \tilde \theta \;v'\frac{{\partial \tilde \theta }}{{\partial y}}
\end{array} \right),
$
|
(91) |
|
$
{e_4} = - \gamma \left(\begin{array}{l}
\tilde \theta \;\overline u \frac{{\partial \theta '}}{{\partial x}}\; + \tilde \theta \;\overline v \frac{{\partial \theta '}}{{\partial y}} + \tilde \theta \;\tilde u\frac{{\partial \theta '}}{{\partial x}} + \tilde \theta \;\tilde v\frac{{\partial \theta '}}{{\partial y}} + \\
\;\;\;\tilde \theta \;u'\frac{{\partial \theta '}}{{\partial x}} + \tilde \theta \;v'\frac{{\partial \theta '}}{{\partial y}}
\end{array} \right),
$
|
(92) |
|
$
{e_5} = - \left({\frac{{\tilde \theta }}{{\overline \theta }}\overline w g} \right),
$
|
(93) |
|
$
{e_6} = - \left({\frac{{\tilde \theta }}{{\overline \theta }}\tilde wg} \right),
$
|
(94) |
|
$
{e_7} = - \left({\frac{{\tilde \theta }}{{\overline \theta }}w'g} \right),
$
|
(95) |
|
$
{e_8} = \gamma \frac{{\tilde \theta }}{{{c_p}}}{\left({\frac{p}{{{p_0}}}} \right)^{R/{{c}_{p}}}}\left({\overline Q + \tilde Q + Q'} \right),
$
|
(96) |
进一步化简方程(88),得到:
|
$
\begin{array}{l}
\partial \tilde{A}/\partial \ t= \frac{\partial }{{\partial \;t}}\left({\frac{\gamma }{2}{{\tilde \theta }^2}} \right) = {P_{\;\alpha }} + {T_P}_{\;\;(\alpha, L)} + {T_P}_{\;\;(\alpha, \alpha)} + {T_P}_{\;\;(\alpha, \beta)} - \\
{B_{\;(\alpha, L)}} - {B_{\;(\alpha, \alpha)}} - {B_{\;(\alpha, \beta)}} + {D_{\;\alpha }}.
\end{array}
$
|
(97) |
公式(97)中各项的物理意义见表 5。
表 5(Table 5)

表 5 α中尺度系统位能方程(97)中各项的物理意义
Table 5 Physical meanings of individual items in the meso-α scale potential energy equation (97)
| 项 |
|
物理意义 |
| $ \partial \tilde{A}/\partial \ t$ |
|
α中尺度系统位能变率 |
| $ {P_{\;\alpha }}$ |
${e_1} $ |
α中尺度系统与大尺度背景场和β中小尺度系统位能之间的相互作用 |
| $ {T_P}_{\;(\alpha, L)}$ |
$ {e_2}$ |
大尺度背景场向α中尺度系统的位能转换项 |
| ${T_P}_{\;(\alpha, \alpha)} $ |
$ {e_3}$ |
α中尺度系统位能的水平输送 |
| ${T_P}_{\;(\alpha, \beta)} $ |
$ {e_4}$ |
β中小尺度系统向α中尺度系统的位能转换项 |
| $ {B_{\;(\alpha, L)}}$ |
$ {e_5}$ |
α中尺度系统气团受到的浮力在大尺度背景场垂直气流中的做功项 |
| ${B_{\;(\alpha, \alpha)}} $ |
$ {e_6}$ |
α中尺度系统气团受到的浮力在α中尺度系统垂直气流中的做功项 |
| ${B_{\;(\alpha, \beta)}} $ |
${e_7} $ |
α中尺度系统气团受到的浮力在β中小尺度系统垂直气流中的做功项 |
| ${D_{\;\alpha }} $
|
$ {e_8}$ |
α中尺度系统非绝热加热做功 |
|
表 5 α中尺度系统位能方程(97)中各项的物理意义
Table 5 Physical meanings of individual items in the meso-α scale potential energy equation (97)
|
2.3.3 计算$ \tilde{\theta }\times (4)$,求${\partial \overline{A}}/{\partial \ t}\; $
|
$
\begin{array}{l}
\partial \bar{A}/\partial \ t = \frac{\partial }{{\partial \;t}}\left({\frac{\gamma }{2}{{\overline \theta }^2}} \right) = {f_1} + {f_2} + {f_3} + {f_4} + {f_5} + \\
{f_6} + {f_7} + {f_8},
\end{array}
$
|
(98) |
|
$
{f_1} = - \left[ {\gamma \;\overline \theta \frac{{\partial \left({\tilde \theta + \theta '} \right)}}{{\partial t}}} \right],
$
|
(99) |
|
$
{f_2} = - \gamma \left[ \begin{array}{l}
\overline \theta \;\overline u \frac{{\partial \overline \theta }}{{\partial x}}\; + \overline \theta \;\overline v \frac{{\partial \overline \theta }}{{\partial y}} + \overline \theta \;\tilde u\frac{{\partial \overline \theta }}{{\partial x}} + \overline \theta \;\tilde v\frac{{\partial \overline \theta }}{{\partial y}} + \\
\;\;\;\overline \theta \;u'\frac{{\partial \overline \theta }}{{\partial x}} + \overline \theta \;v'\frac{{\partial \overline \theta }}{{\partial y}}
\end{array} \right],
$
|
(100) |
|
$
{f_3} = - \gamma \left[ \begin{array}{l}
\overline \theta \;\overline u \frac{{\partial \tilde \theta }}{{\partial x}}\; + \overline \theta \;\overline v \frac{{\partial \tilde \theta }}{{\partial y}} + \overline \theta \;\tilde u\frac{{\partial \tilde \theta }}{{\partial x}} + \overline \theta \;\tilde v\frac{{\partial \tilde \theta }}{{\partial y}} + \\
\;\;\;\;\overline \theta \;u'\frac{{\partial \tilde \theta }}{{\partial x}} + \overline \theta \;v'\frac{{\partial \tilde \theta }}{{\partial y}}
\end{array} \right],
$
|
(101) |
|
$
{f_4} = - \gamma \left[ \begin{array}{l}
\overline \theta \;\overline u \frac{{\partial \theta '}}{{\partial x}}\; + \overline \theta \;\overline v \frac{{\partial \theta '}}{{\partial y}} + \overline \theta \;\tilde u\frac{{\partial \theta '}}{{\partial x}} + \overline \theta \;\tilde v\frac{{\partial \theta '}}{{\partial y}} + \\
\;\;\;\;\overline \theta \;u'\frac{{\partial \theta '}}{{\partial x}} + \overline \theta \;v'\frac{{\partial \theta '}}{{\partial y}}
\end{array} \right],
$
|
(102) |
|
$
{f_5} = - \left({\frac{{\overline \theta }}{{\overline \theta }}\overline w g} \right),
$
|
(103) |
|
$
{f_6} = - \left({\frac{{\overline \theta }}{{\overline \theta }}\tilde wg} \right),
$
|
(104) |
|
$
{f_7} = - \left({\frac{{\overline \theta }}{{\overline \theta }}w'g} \right),
$
|
(105) |
|
$
{f_8} = \gamma \frac{{\overline \theta }}{{{c_p}}}{\left({\frac{p}{{{p_0}}}} \right)^{R/{{c}_{p}}}}\left({\overline Q + \tilde Q + Q'} \right),
$
|
(106) |
进一步化简方程(98),得到:
|
$
\begin{array}{l}
\partial \bar{A}/\partial \ t = \frac{\partial }{{\partial \;t}}\left({\frac{\gamma }{2}{{\overline \theta }^2}} \right) = {P_{\;L}} + {T_P}_{\;\;(L, L)} + {T_P}_{\;\;(L, \alpha)} + {T_P}_{\;\;(L, \beta)} - \\
{B_{\;\;(L, L)}} - {B_{\;\;(L, \alpha)}} - {B_{\;\;(L, \beta)}} + {D_{\;L}}.
\end{array}
$
|
(107) |
公式(107)中各项的物理意义见表 6。
表 6(Table 6)

表 6 大尺度背景场位能方程(107)中各项的物理意义
Table 6 Physical meanings of individual items in the large scale background field potential energy equation (107)
| 项 |
|
物理意义 |
| $\partial \bar{A}/\partial \ t $ |
|
大尺度背景场位能变率 |
| ${P_{\;L}} $ |
$ {f_1}$ |
大尺度背景场与α中尺度系统和β中小尺度系统位能之间的相互作用 |
| $ {T_P}_{\;(L, L)}$ |
${f_2} $ |
大尺度背景场位能的水平输送 |
| ${T_P}_{\;(L, \alpha)} $ |
${f_3} $ |
α中尺度系统向大尺度背景场的位能转换项 |
| $ {T_P}_{\;(L, \beta)}$ |
${f_4} $ |
β中小尺度系统向大尺度背景场的位能转换项 |
| $ {B_{\;\;(L, L)}}$ |
$ {f_5}$ |
大尺度背景场气团受到的浮力在大尺度背景场垂直气流中的做功项 |
| ${B_{\;\;(L, \alpha)}} $ |
$ {f_6}$ |
大尺度背景场气团受到的浮力在α中尺度系统垂直气流中的做功项 |
| ${B_{\;\;(L, \beta)}} $ |
${f_7} $ |
大尺度背景场气团受到的浮力在β中小尺度系统垂直气流中的做功项 |
| ${D_{\;L}} $
|
${f_8} $ |
大尺度背景场非绝热加热做功 |
|
表 6 大尺度背景场位能方程(107)中各项的物理意义
Table 6 Physical meanings of individual items in the large scale background field potential energy equation (107)
|
3 结论与讨论
上述推导的三种尺度的动能方程和位能方程比两种尺度的动能方程和位能方程复杂的多,所以它们之间的相互作用或者能量转换过程也相对复杂一些。动能方程中,除了与位能方程的转换项之外,还包括动能之间的转换、水平气压梯度力做功、垂直方向扰动气压梯度力做功、地转偏向力做功项、摩擦力做功项以及空气的压缩效应。一般情况下,地转偏向力做功为零,但是地转偏向力的分量做功不一定为零。空气的压缩效应项是指由于温度的变化导致气压的变化,气压的变化会使得空气收缩或者膨胀,这是扰动气压做功的另外一种形式。各个尺度动能之间的能量转换主要是由各个尺度的风速大小和风切变决定。位能方程中,除了与动能方程的转换项之外,还包括位能之间的转换以及非绝热加热所做的贡献。各个尺度位能之间的能量转换主要是由于位温或温度的水平分布不均匀造成的,在各个尺度风速的作用下发生温度平流。
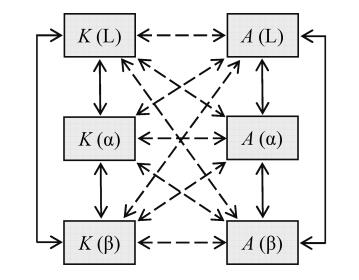
大尺度背景场、α中尺度和β中小尺度系统能量之间可以两两相互转换,比如β中小尺度系统位能除了可以把能量转化给α中尺度系统位能和β中小尺度系统动能,还可以转化给大尺度背景场位能、动能以及α中尺度系统动能。其它尺度的动能和位能也是如此。在暴雨过程中,水平和垂直速度变大,动能增大,不同尺度的动能之间会发生正压能量转换;非绝热加热过程是位能增大的主要来源,位能向动能的斜压能量转换是暴雨发展的最重要的条件,它们之间的能量转换大致如图 1所示,图中虚线表示三个尺度间动能和位能之间的能量转换,实线表示的是动能之间的能量转换和位能之间的能量转换。仔细对比动能方程和位能方程,方程中都包含BW项(浮力做功项),当同一水平面上出现正的温度扰动,就会受到向上的浮力,在向上的垂直气流中浮力做功,将位能转换成动能,这是暴雨发生发展的最重要的机制。其他项或多或少都对暴雨的发展和消亡产生一定的作用,它们之间的能量是如何相互转化的,其中哪些项对暴雨发展的贡献比较大,这些都有待后续的研究。
参考文献
|
Hsu P C, Li T, Tsou C H. 2011. Interactions between boreal summer intraseasonal oscillations and synoptic-scale disturbances over the western North Pacific. Part Ⅰ:Energetics diagnosis [J]. J. Climate, 24(3): 927-941. DOI:10.1175/2010JCLI3833.1
|
|
Kanzawa H. 1984. Quasi-geostrophic energetics based on a transformed Eulerian equation with application to wave-tonal flow interaction problems [J]. J. Meteor. Soc. Japan, 62(1): 36-51. DOI:10.2151/jmsj1965.62.1_36
|
廖移山, 李俊, 王晓芳, 等. 2010. 2007年7月18日济南大暴雨的β中尺度分析[J]. 气象学报, 68(6): 944-956. Liao Yishan, Li Jun, Wang Xiaofang, et al. 2010. A meso-β scale analysis of the torrential rain event in Jinan in 18 July 2007 (in Chinese)[J]. Acta Meteorologica Sinica, 68(6): 944-956. DOI:10.11676/qxxb2010.089
|
Lorenz E N. 1955. Available potential energy and the maintenance of the general circulation [J]. Tellus, 7(2): 157-167. DOI:10.3402/tellusa.v7i2.8796
|
Murakami S. 2011. Atmospheric local energetics and energy interactions between mean and eddy fields. Part Ⅰ:Theory [J]. J. Atmos. Sci., 68(4): 760-768. DOI:10.1175/2010JAS3664.1
|
|
|
寿绍文. 2009. 中尺度气象学[M]. 北京: 气象出版社. Shou Shaowen. 2009. Mesoscale Meteorology (in Chinese)[M]. Beijing: China Meteorological Press.
|
孙晶. 2011. 梅雨锋暴雨中尺度对流系统研究若干进展[J]. 气象科技, 39(3): 257-265. Sun Jing. 2011. Advances in researches on meso-scale convective systems related to Meiyu heavy rainfall (in Chinese)[J]. Meteorological Science and Technology, 39(3): 257-265. DOI:10.3969/j.issn.1671-6345.2011.03.001
|
王建捷, 李泽椿. 2002. 1998年一次梅雨锋暴雨中尺度对流系统的模拟与诊断分析[J]. 气象学报, 60(2): 146-155. Wang Jianjie, Li Zechun. 2002. Numerical simulation and diagnostic analysis on mesoscale convective systems of a torrential rain case in Meiyu period of 1998 (in Chinese)[J]. Acta Meteorologica Sinica, 60(2): 146-155. DOI:10.11676/qxxb2002.018
|
 2018, Vol. 42
2018, Vol. 42

