1 引言

近些年，国内科研和业务中应用的中尺度模式主要有国外引进的WRF（Weather Research and Forecasting Model; Skamarock et al., 2005），我国自主发展的GRAPES（Global and Regional Assimilation and PrEdiction System; 薛纪善和陈德辉，2008）和AREM（Advanced Regional Eta- coordinate Model; 宇如聪和徐幼平, 2004）。其中，AREM模式是一个由我国科学家自主设计和开发的适合我国地形和气候特点且具有良好业务应用效果的有限区域数值预报模式。AREM模式根据我国暴雨特点并吸收了国内和国际上一些中尺度模式的长处，比如采用$\eta $坐标作为垂直坐标，抓住了东亚区域的地形和暴雨特点（宇如聪, 1989）；充分考虑暴雨模式中水汽等要素的强梯度分布特征，采用了更有物理意义的水汽平流计算方案（Yu, 1994, 1995）；避免了其他模式为了稳定运行而不得不进行的强耗散和平滑处理等。利用该模式先后对青藏高原背风气旋的生成发展、我国受地形影响最为典型的暴雨现象—“雅安天漏”（宇如聪, 1992）、“75.8”河南特大暴雨（蔡则怡和宇如聪, 1997）、“98.7”武汉暴雨及“03.7”淮河暴雨（宇如聪等, 2004）等作了成功的数值模拟。该模式也在原联参气象水文空间天气总站、空军气象中心、二炮气象中心、黄河水利委员会水文局、湖北、湖南等气象中心业务化运行，取得了良好的经济、军事和社会效益。

随着人们对暴雨数值预报精度的要求越来越高，AREM模式也在不断发展和完善中。近些年，该模式先后实现了并行计算功能（普业等, 2008），显式云和降水预报功能（宇如聪和徐幼平, 2004），气象资料四维变分同化功能（王斌和赵颖, 2005）等。当前，AREM模式已具有较细的模式分辨率、较高的模块化程度、较先进的同化模块和物理过程，多年科研和业务应用充分证实该模式对东亚区域暴雨预报有优势（宇如聪, 1994; 史历, 2003; 宇如聪和徐幼平, 2004; 倪允琪和周秀骥, 2004）。随着中尺度模式分辨率不断提高，特别是模式水平网格距小于5 km时，就需要考虑大气非静力平衡特性。为此，发展该模式的非静力框架势在必行。

通常而言，中尺度非静力框架有两种构建方法。其一、基于云模式创建，像ARPS（Advanced Regional Prediction System）和RAMS（Regional Atmospheric Modeling System）。ARPS最初的开发动机是进行时间尺度几小时、空间范围几百公里的风暴尺度天气预警，但伴随其资料同化及分析系统的建立和完善、物理过程的不断改进以及模式后处理的开发，ARPS逐渐成为一个区域数值预报模式（Xue et al., 1995）。RAMS则是云模式和中尺度模式的结合，它继承了云模式小尺度动力过程的优秀计算方法和微物理过程，以及中尺度模式模拟中尺度过程的经验和陆面对大气的影响，当前已经扩展到半球甚至全球的中尺度或大尺度天气系统模拟（Walko et al., 1995）。其二、基于静力框架扩建，由于数值天气预报需要处理更大时空范围的运动，因此比对流云尺度和风暴尺度的非静力模式设计难度更大，如在业务环境中很难处理质量的不确定盈亏。另外，非静力动力过程和数值计算可以在高层产生虚假运动，此时为了解决该问题而强迫模式上层变量达到一个定常状态对于数值天气预报并不合适（Janjic and Gerrity, 2001）。因此，在静力平衡模式基础之上扩充非静力功能便成为一些业务预报模式的选择。

MM5（Pennsylvania State University-NCAR Mesoscale Model）的非静力版本（Dudhia, 1993）构建出发点即要能与静力版本兼容和一致。一些计算模块如水汽处理、平流、扩散、辐射、边界层、陆面、对流参数化等经过很少改动即可在非静力模式中得到使用。这种作法的优势在于能够尽可能地保留静力平衡模式的优势，特别是在较大尺度非静力模拟之时。Dudhia（1993）对静力框架的修正主要包括：其一、增加半隐式声波处理，替换气压—动量计算关系；其二、增加垂直运动和气压扰动预报方程。

同样，Janjic and Gerrity（2001）提出通过对静力气压垂直坐标表达的静力近似进行松弛实现非静力计算的方法，并成功应用于WRF-NMM（Weather Research and Forecasting model- Nonhydrostatic Mesoscale Model）。Janjic and Gerrity（2001）将模式方程组分为两部分，其一为静力系统，其二即为由于引入垂直加速度而带来的高阶订正。这种方案也能尽量保留静力平衡模式的优势，还可以让我们清楚地知道非静力订正的具体影响（什么地方存在影响、如何影响、影响到什么程度）。另外，此方法简化了静力平衡和非静力模拟的转换和比较，这对于统一的全球和区域预报系统具有更大优势。赵滨（2008）沿用Janjic and Gerrity（2001）的方法建立了非静力全球谱模式，该设计思想也是本文构造AREM非静力框架的重要参考。

数值模式设计中垂直坐标的选择，Gallus and Klemp（2000）给出了考量方法，如使用最小的垂直精度有效表达大气活动的垂直尺度与结构、适合于地形处理、所要描述的现象能否被选用的垂直坐标更好地刻画等方面。对于水平网格的选取，在中尺度大气数值模拟中采用跳点C网格、半跳点B和E网格效果更好（Sun, 1984; Mesinger, 1988; 宇如聪, 1994）；但需要注意的是，也有模式仍然采用非跳点A网格，并成功进行静力和非静力模拟（Wang, 2001, 2007）。

对于中尺度数值模式而言，较高的水平和垂直分辨率对稳定积分所需的时间步长要求严格，而且为了更有效地处理重力外波和声波，模式时间积分方案通常采用显式时间分离算法或隐式计算方法。根据Saito et al.（1998）的研究，相比于半隐式方案，对于业务预报而言，显式分离方法更有效。

2 非静力方程组 2.1 基本动力方程组

2.1.1 $\eta $坐标定义

$ \eta =\sigma \cdot {{\eta }_\text{s}}=\frac{\pi -{{\pi }_\text{t}}}{{{\pi }_\text{s}}-{{\pi }_\text{t}}}{{\eta }_\text{s}}, $

(1)

其中，

$ {{\eta }_\text{s}}=\frac{{{\pi }_\text{rf}}({{z}_\text{s}})-{{\pi }_\text{t}}}{{{\pi }_\text{rf}}({{z}_\text{b}})-{{\pi }_\text{t}}}, $

(2)

令

$ {{P}^{2}}=\frac{{{\pi }_\text{s}}-{{\pi }_\text{t}}}{{{\eta }_\text{s}}}, $

(3)

则

$ \eta =\frac{\pi -{{\pi }_\text{t}}}{{{P}^{2}}}. $

(4)

上述推导中，π表示静力气压，π_t为模式顶气压，π_s为地面气压，π_rf为参考气压，z_s表示地形高度，z_b为参考高度。

2.1.2 静力平衡方程推导

由

$ \frac{\partial \mathit{\Phi } }{\partial \pi }=-\alpha, $

(5)

可得到：

$ \frac{\partial \mathit{\Phi } }{\partial \eta }={{P}^{2}}\frac{\partial \mathit{\Phi } }{\partial \pi }=-{{P}^{2}}\frac{RT}{p}, $

(6)

其中，$\alpha $为比容，T为温度，p表示实际气压，$\mathit{\Phi }$表示重力位势，R表示干空气比气体常数。

2.1.3 垂直动量方程推导

对于薄层大气，我们有

$ \frac{dw}{dt}=-\alpha \frac{\partial p}{\partial z}-g=-\alpha g\frac{\partial p}{\partial \mathit{\Phi } }-g=-g+g\frac{\partial p}{\partial \pi }, $

(7)

其中，w为垂直速度，z表示位势高度，g表示重力加速度。

定义高阶订正参数：

$ \varepsilon =\frac{\text{1}}{g}\frac{\text{d}w}{\text{d}t}, $

(8)

则第三运动方程可写为

$ \frac{\partial p}{\partial \pi }=\text{1}+\varepsilon . $

(9)

2.1.4 非静力连续方程

$ w=\frac{\text{d}z}{\text{d}t}=\frac{\text{1}}{g}\frac{\text{d}\mathit{\Phi } }{\text{d}t}=\frac{\text{1}}{g}\left(\frac{\partial \mathit{\Phi } }{\partial t}+V\cdot {{\nabla }_{\eta }}\mathit{\Phi } + \dot{\eta }\frac{\partial \mathit{\Phi } }{\partial \eta } \right), $

(10)

其中，V表示水平风矢量。

2.1.5 非静力框架下静力气压表达的连续方程推导

对于任意的垂直坐标s，Kasahara（1974）给出：

$ {{\left[ \frac{\partial }{\partial t}\left( \rho \frac{\partial z}{\partial s} \right) \right]}_{s}}+{{\nabla }_{s}}\cdot \left( \rho \boldsymbol {V}\frac{\partial z}{\partial s} \right)+\frac{\partial \left( \rho \dot{s}\frac{\partial z}{\partial s} \right)}{\partial s}=\text{0}, $

(11)

其中，$\rho $表示密度。在$\eta $坐标下，（11）式表示为

$ \frac{\partial }{\partial t}\left(\rho \frac{\partial \mathit{\Phi } }{\partial \eta } \right)+{{\nabla }_{\eta }}\cdot \left(\rho V\frac{\partial \mathit{\Phi } }{\partial \eta } \right)+\frac{\partial \left(\rho \dot{\eta }\frac{\partial \mathit{\Phi } }{\partial \eta } \right)}{\partial \eta }=\text{0}. $

(12)

将$\partial \mathit{\Phi } /\partial \eta =-{{P}^{\text{2}}}\alpha $代入上式，可得

$ \frac{\partial {{P}^{\text{2}}}}{\partial t}+{{\nabla }_{\eta }}\cdot ({{P}^{\text{2}}}\boldsymbol {V})+\frac{\partial ({{P}^{\text{2}}}\dot{\eta })}{\partial \eta }=\text{0}. $

(13)

对上式进行积分，并注意垂向刚体边界，得到：

$ \frac{\partial {{P}^{\text{2}}}}{\partial t}=-\frac{\text{1}}{{{\eta }_{s}}}\int{{{\nabla }_{\eta }}\cdot ({{P}^{\text{2}}}\boldsymbol {V})\text{d}\eta }. $

(14)

同理可有

$ {{P}^{\text{2}}}\dot{\eta }=-\eta \frac{\partial {{P}^{\text{2}}}}{\partial t}-\int{{{\nabla }_{\eta }}\cdot ({{P}^{\text{2}}}\boldsymbol {V})\text{d}\eta }. $

(15)

2.1.6 气压梯度力推导

$ \begin{align} &{{\nabla }_{z}}p={{\nabla }_{\eta }}p-\frac{\partial p}{\partial \pi }{{P}^{\text{2}}}\frac{\partial \eta }{\partial z}{{\nabla }_{\eta }}z={{\nabla }_{\eta }}p-\left(\text{1}+\varepsilon \right){{P}^{\text{2}}}\frac{\partial \eta }{\partial \mathit{\Phi } }{{\nabla }_{\eta }}\mathit{\Phi } \\ &\;\;\;\;\;\;\;\;={{\nabla }_{\eta }}p+\left(\text{1}+\varepsilon \right)\frac{\text{1}}{\alpha }{{\nabla }_{\eta }}\mathit{\Phi }, \\ \end{align} $

(16)

由此可得水平动量方程为

$ \frac{\text{d}\mathit{\boldsymbol{V}}}{\text{d}t}=-\left(\text{1}+\varepsilon \right){{\nabla }_{\eta }}\mathit{\Phi }-\alpha {{\nabla }_{\eta }}p-f\mathit{\boldsymbol{k}}\times \mathit{\boldsymbol{V}}, $

(17)

其中，f为科氏参数。

2.1.7 热力学方程推导

假设为绝热情形，则有

$ {{c}_{p}}\frac{\text{d}T}{\text{d}t}=\alpha \frac{\text{d}p}{\text{d}t}, $

(18)

即：

$ \begin{align} &\frac{\partial T}{\partial t}=-\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}T-\dot{\eta }\frac{\partial T}{\partial \eta }+\frac{\alpha }{{{c}_{p}}}\frac{\text{d}p}{\text{d}t}=-\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}T-\dot{\eta }\frac{\partial T}{\partial \eta }+ \\ &\;\;\;\;\;\frac{\alpha }{{{c}_{p}}}\omega =-\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}T-\dot{\eta }\frac{\partial T}{\partial \eta }+\frac{\alpha }{{{c}_{p}}}({{\omega }_{\text{1}}}+{{\omega }_{\text{2}}}), \\ \end{align} $

(19)

其中，c_p表示比定压热容，下面对（19）式进行分解计算。注意气压可写为如下形式：

$ p=p\left[ x, y, \pi \left(x, y, z, t \right), t \right], $

(20)

则可得

$ \frac{\partial p}{\partial t}=\frac{\partial p}{\partial {{t}_{\pi }}}+{{\frac{\partial p}{\partial \pi }}_{t}}\cdot \frac{\partial \pi }{\partial t}=\frac{\partial p}{\partial {{t}_{\pi }}}+(\text{1}+\varepsilon)\frac{\partial \pi }{\partial t}. $

(21)

又由下述表达式：

$ \dot{\eta }\frac{\partial p}{\partial \eta }=\dot{\eta }\frac{\partial p}{\partial \pi }\frac{\partial \pi }{\partial \eta }=\dot{\eta }(\text{1}+\varepsilon)\frac{\partial \pi }{\partial \eta }, $

(22)

可以得到：

$ \begin{align} &\frac{\text{d}p}{\text{d}t}=\frac{\partial p}{\partial t}+\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}p+\dot{\eta }\frac{\partial p}{\partial \eta }=\frac{\partial p}{\partial {{t}_{\pi }}}+(1+\varepsilon)\frac{\partial \pi }{\partial t}+ \\ &\;\;\;\;\;\;\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}p+\dot{\eta }(1+\varepsilon)\frac{\partial \pi }{\partial \eta }={{\omega }_{1}}+{{\omega }_{2}}, \\ \end{align} $

(23)

其中，

$ {{\omega }_{\text{1}}}=(\text{1}+\varepsilon)\frac{\partial \pi }{\partial t}+\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}p+\dot{\eta }(\text{1}+\varepsilon)\frac{\partial \pi }{\partial \eta }, $

(24)

$ {{\omega }_{\text{2}}}=\frac{\partial p}{\partial {{t}_{\pi }}}. $

(25)

${{\omega }_{\text{1}}}$还可以进一步变形为

$ \begin{align} &{{\omega }_{\text{1}}}=(\text{1}+\varepsilon)\left(\frac{\partial \pi }{\partial t}+\dot{\eta }\frac{\partial \pi }{\partial \eta } \right)+\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}p \\ &\text{ }=(\text{1}+\varepsilon)\left[ \frac{\partial \pi }{\partial t}-\eta \frac{\partial {{P}^{\text{2}}}}{\partial t}-\int{{{\nabla }_{\eta }}\cdot ({{P}^{\text{2}}}\mathit{\boldsymbol{V}})d\eta } \right]+\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}p \\ &\text{ }=\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}p-\left(\text{1}+\varepsilon \right)\int{{{\nabla }_{\eta }}\cdot ({{P}^{\text{2}}}\mathit{\boldsymbol{V}})d\eta .} \\ \end{align} $

(26)

因此，热力学方程可以分解如下两部分：

$ \begin{align} & {{\left(\frac{\partial T}{\partial t} \right)}_{\text{1}}}=-\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}T-\dot{\eta }\frac{\partial T}{\partial \eta }+\frac{\alpha {{\omega }_{1}}}{{{c}_{p}}}=-\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}T- \\ & \dot{\eta }\frac{\partial T}{\partial \eta }+\frac{\alpha }{{{c}_{p}}}\left[ \mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}p-(\text{1}+\varepsilon)\int{{{\nabla }_{\eta }}\cdot \left({{P}^{\text{2}}}\mathit{\boldsymbol{V}} \right)\text{d}\eta } \right], \\ \end{align} $

(27)

$ {{\left(\frac{\partial T}{\partial t} \right)}_{\text{2}}}=\frac{\alpha {{\omega }_{2}}}{{{c}_{p}}}=\frac{\alpha }{{{c}_{p}}}{{\left(\frac{\partial p}{\partial t} \right)}_{\pi }}. $

(28)

2.1.8 高阶订正参数定义

$ \varepsilon =\frac{\text{d}w}{g\text{d}t}=\frac{\text{1}}{g}\left(\frac{\partial w}{\partial t}+\mathit{\boldsymbol{V}}\cdot {{\nabla }_{\eta }}w+ \dot{\eta }\frac{\partial w}{\partial \eta } \right). $

(29)

2.1.9 气体状态方程

$ \alpha =\frac{RT}{p}. $

(30)

2.2 标准层结扣除及扰动方程组 2.2.1 扣除假设

为了减小大气动力方程组在数值计算中常出现的“大项小差”而产生的计算误差，我们将保留AREM静力平衡框架的静力扣除思想，并在等压面引进标准层结近似。因为即使存在强对流时，$\partial p/\partial z$的静压部分约占其本身的99%（廖洞贤等，2008），因此我们可以认为实际气压与高度也存在单调对应关系，可以使用p坐标进行扰动分析。

设标准层结廓线为

$ \left\{ \begin{align} &\tilde{T}=\tilde{T}(p), \\ &\tilde{\mathit{\Phi } }=\tilde{\mathit{\Phi } }(p), \\ \end{align} \right. $

(31)

其中，$\tilde{T}$和$\mathit{\tilde{\Phi }}$为标准层结温度和位势，并满足：

$ R\tilde{T}=-p\frac{\partial \mathit{\tilde{\Phi }}}{\partial \pi }=-p\frac{\partial \mathit{\tilde{\Phi }}}{\partial p}\frac{\partial p}{\partial \pi }=-(\text{1}+\varepsilon)p\frac{\partial \mathit{\tilde{\Phi }}}{\partial p}, $

(32)

令

$ \left\{ \begin{align} & T\left(\lambda, \theta, p, t \right)=\tilde{T}\left(p \right)+T'\left(\lambda, \theta, p, t \right), \\ & \mathit{\Phi }\left(\lambda, \theta, p, t \right)=\mathit{\tilde{\Phi }}\left(p \right)+\mathit{\Phi }'\left(\lambda, \theta, p, t \right), \\ \end{align} \right. $

(33)

其中，λ、θ分别表示经度和余纬（90°－纬度），T'和$\mathit{{\Phi }'}$表示扰动温度和位势。得到p坐标下扰动形式的静力平衡方程为

$ R{T}'=-(\text{1}+\varepsilon)p\frac{\partial \mathit{{\Phi }'}}{\partial p}\text{ }. $

(34)

2.2.2 水平气压梯度力的变换

z坐标系下水平气压梯度力在p坐标系下可表示为

$ -\alpha {{\nabla }_{z}}p=-\left(\text{1}+\varepsilon \right){{\nabla }_{p}}\mathit{\Phi }. $

(35)

在p坐标下进行气压梯度力的扰动分离，可得

$ -\left(\text{1}+\varepsilon \right){{\nabla }_{p}}\mathit{\Phi }=-\left(\text{1}+\varepsilon \right){{\nabla }_{p}}\mathit{{\Phi }'}\text{ }, $

(36)

再将p坐标下扰动气压梯度力转换到$\eta $坐标中可得

$ \begin{align} & -\left(\text{1}+\varepsilon \right){{\nabla }_{p}}\mathit{{\Phi }'}=-\left(\text{1}+\varepsilon \right){{\nabla }_{\eta }}\mathit{{\Phi }'}+\left(\text{1}+\varepsilon \right)\frac{\partial \mathit{{\Phi }'}}{\partial p}{{\nabla }_{\eta }}p \\ & \ \ \ =-\left(\text{1}+\varepsilon \right){{\nabla }_{\eta }}\mathit{{\Phi }'}+\left(\text{1}+\varepsilon \right)\left(-\frac{R{T}'}{p}\frac{\text{1}}{\text{1}+\varepsilon } \right){{\nabla }_{\eta }}p \\ & \ \ \ =-\left(\text{1}+\varepsilon \right){{\nabla }_{\eta }}\mathit{{\Phi }'}-\frac{R{T}'}{p}{{\nabla }_{\eta }}p\text{ }. \\ \end{align} $

(37)

基于上述推导，第一运动方程（即纬向风方程）只有气压梯度力发生变换：

$ -\frac{\text{1}+\varepsilon }{a\text{sin}\theta }\frac{\partial \mathit{{\Phi }'}}{\partial \lambda }-\frac{RT'}{p}\frac{\text{1}}{a\text{sin}\theta }\frac{\partial p}{\partial \lambda }\text{ }, $

(38)

其中，$a$表示地球半径。同理，第二运动方程（即经向风方程）也只有气压梯度力发生变换：

$ -\frac{\text{1}+\varepsilon }{a}\frac{\partial \mathit{{\Phi }'}}{\partial \theta }-\frac{R{T}'}{p}\frac{\text{1}}{a}\frac{\partial p}{\partial \theta }. $

(39)

2.2.3 垂直速度表达

$ \begin{align} & w=\frac{\text{1}}{g}\left(\frac{\partial \mathit{{\Phi }'}}{\partial t}+\frac{u}{a\text{sin}\theta }\frac{\partial \mathit{{\Phi }'}}{\partial \lambda }+\frac{v}{a}\frac{\partial \mathit{{\Phi }'}}{\partial \theta }+\dot{\eta }\frac{\partial \left(\mathit{\tilde{\Phi }}+\mathit{{\Phi }'} \right)}{\partial \eta } \right) \\ & =\frac{\text{1}}{g}\left(\frac{\partial \mathit{{\Phi }'}}{\partial t}+\frac{u}{a\text{sin}\theta }\frac{\partial \mathit{{\Phi }'}}{\partial \lambda }+\frac{v}{a}\frac{\partial \mathit{{\Phi }'}}{\partial \theta }+\dot{\eta }\frac{\partial \mathit{\tilde{\Phi }}}{\partial \eta }+\dot{\eta }\frac{\partial \mathit{{\Phi }'}}{\partial \eta } \right) \\ & =\frac{\text{1}}{g}\left(\frac{\partial \mathit{{\Phi }'}}{\partial t}+\frac{u}{a\text{sin}\theta }\frac{\partial \mathit{{\Phi }'}}{\partial \lambda }+\frac{v}{a}\frac{\partial \mathit{{\Phi }'}}{\partial \theta }+\dot{\eta }\frac{\partial \mathit{{\Phi }'}}{\partial \eta }-{{P}^{\text{2}}}\dot{\eta }\frac{R\tilde{T}}{p} \right). \\ \end{align} $

(40)

2.2.4 热力学方程的变换

热力学能量方程进行扰动分离后，可得

$ {{c}_{p}}\frac{\text{d}\tilde{T}}{\text{d}t}+{{c}_{p}}\frac{\text{d}{T}'}{\text{d}t}=\frac{R\tilde{T}}{p}\left({{\omega }_{\text{1}}}+{{\omega }_{2}} \right)+\frac{R{T}'}{p}\left({{\omega }_{\text{1}}}+{{\omega }_{2}} \right), $

(41)

整理后得

$ {{c}_{p}}\frac{\text{d}{T}'}{\text{d}t}=\left(\frac{R\tilde{T}}{p}-{{c}_{p}}\frac{\partial \tilde{T}}{\partial p} \right)\left({{\omega }_{\text{1}}}+{{\omega }_{2}} \right)+\frac{R{T}'}{p}\left({{\omega }_{\text{1}}}+{{\omega }_{2}} \right). $

(42)

考虑下述关系时，由于$\varepsilon $为高阶小量，其以系数出现时可以忽略，所以，

$ \begin{align} &R\left(\frac{R\tilde{T}}{p}-{{c}_{p}}\frac{\partial \tilde{T}}{\partial p} \right)={{c}_{p}}\frac{{{R}^{\text{2}}}\tilde{T}}{gp}\left(\frac{g}{{{c}_{p}}}+\frac{\text{1}}{\text{1}+\varepsilon }\frac{\partial \tilde{T}}{\partial z} \right)\approx \\ &{{c}_{p}}\frac{{{R}^{\text{2}}}\tilde{T}}{gp}\left(\frac{g}{{{c}_{p}}}+\frac{\partial \tilde{T}}{\partial z} \right)={{c}_{p}}\frac{{{R}^{\text{2}}}\tilde{T}}{gp}({{\gamma }_{d}}-\tilde{\gamma }), \\ \end{align} $

(43)

并令常定重力波速表达为

$ {{{\tilde{c}}}^{\text{2}}}=\frac{{{R}^{\text{2}}}\tilde{T}}{g}\left({{\gamma }_{d}}-\tilde{\gamma } \right)\text{, } $

(44)

因此有

$ R\left(\frac{R\tilde{T}}{p}-{{c}_{p}}\frac{\partial \tilde{T}}{\partial p} \right)={{c}_{p}}\frac{{{{\tilde{c}}}^{\text{2}}}}{p}. $

(45)

最终得到扰动热力学方程为

$ \frac{\text{d}{T}'}{\text{d}t}=\frac{{{{\tilde{c}}}^{\text{2}}}}{pR}({{\omega }_{\text{1}}}+{{\omega }_{2}})+\frac{R{T}'}{{{c}_{p}}p}({{\omega }_{\text{1}}}+{{\omega }_{2}})\text{ }. $

(46)

2.3 IAP(Institute of Atmospheric Physics)变换及最终方程组 2.3.1 第一和第二运动方程

令

$ \left\{ \begin{align} &U=Pu, \\ &V=Pv, \\ \end{align} \right. $

(47)

对扰动形式的水平动量方程两边同乘以P，经过整理可得

$ \begin{array}{l} {\begin{array}{l} \frac{{\partial U}}{{\partial t}} = - \frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\left({\frac{{\partial Uu}}{{\partial \lambda }} - \frac{U}{{\rm{2}}}\frac{{\partial u}}{{\partial \lambda }}} \right) - \frac{{\rm{1}}}{{a{\rm{sin}}\theta }} \cdot \\ {\rm{ }}\left({\frac{{\partial Uv{\rm{sin}}\theta }}{{\partial \theta }} - \frac{U}{{\rm{2}}}\frac{{\partial v{\rm{sin}}\theta }}{{\partial \theta }}} \right) - \left({\frac{{\partial U\dot \eta }}{{\partial \eta }} - \frac{U}{{\rm{2}}}\frac{{\partial \dot \eta }}{{\partial \eta }}} \right) - \frac{{\left({{\rm{1}} + \varepsilon } \right)P}}{{a{\rm{sin}}\theta }} \cdot {\rm{ }} \end{array}}\\ \frac{{\partial \mathit{\Phi '}}}{{\partial \lambda }} - \frac{{\Pi '\tilde c}}{p}\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\frac{{\partial p}}{{\partial \lambda }} - \left({{\rm{2}}\mathit{\Omega }{\rm{cos}}\theta + \frac{{u{\rm{ctg}}\theta }}{a}} \right)V, \end{array} $

(48)

$ \begin{array}{l} {\begin{array}{l} \frac{{\partial V}}{{\partial t}} = - \frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\left({\frac{{\partial Vu}}{{\partial \lambda }} - \frac{V}{{\rm{2}}}\frac{{\partial u}}{{\partial \lambda }}} \right) - \frac{{\rm{1}}}{{a{\rm{sin}}\theta }} \cdot \\ \left({\frac{{\partial Vv{\rm{sin}}\theta }}{{\partial \theta }} - \frac{V}{{\rm{2}}}\frac{{\partial v{\rm{sin}}\theta }}{{\partial \theta }}} \right) - \left({\frac{{\partial V\dot \eta }}{{\partial \eta }} - \frac{V}{{\rm{2}}}\frac{{\partial \dot \eta }}{{\partial \eta }}} \right) - \frac{{\left({{\rm{1}} + \varepsilon } \right)P}}{a} \cdot \end{array}}\\ {\rm{ }}\frac{{\partial \mathit{\Phi '}}}{{\partial \theta }} - \frac{{\Pi '\tilde c}}{p}\frac{{\rm{1}}}{a}\frac{{\partial p}}{{\partial \theta }} + \left({{\rm{2}}\mathit{\Omega }{\rm{cos}}\theta + \frac{{u{\rm{ctg}}\theta }}{a}} \right)U. \end{array} $

(49)

其中，$\mathit{\Omega }$表示地球旋转角速度，$\mathit{\Pi '}$的表达式为

$ {\mathit{\Pi '} = \frac{R}{{\tilde c}}PT'}. $

(50)

2.3.2 热力学方程

对扰动形式热力学能量方程两端同乘以$RP/\tilde c$，经过整理可得

$ \begin{array}{l} {\begin{array}{l} \frac{{\partial \mathit{\Pi '}}}{{\partial t}} = - \frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\left({\frac{{\partial \mathit{\Pi '}u}}{{\partial \lambda }} - \frac{{\mathit{\Pi '}}}{{\rm{2}}}\frac{{\partial u}}{{\partial \lambda }}} \right) - \frac{{\rm{1}}}{{a{\rm{sin}}\theta }} \cdot \\ {\rm{ }}\left({\frac{{\partial \mathit{\Pi '}v{\rm{sin}}\theta }}{{\partial \theta }} - \frac{{\mathit{\Pi '}}}{{\rm{2}}}\frac{{\partial v{\rm{sin}}\theta }}{{\partial \theta }}} \right) - \left({\frac{{\partial \mathit{\Pi '}\dot \eta }}{{\partial \eta }} - \frac{{\mathit{\Pi '}}}{{\rm{2}}}\frac{{\partial \dot \eta }}{{\partial \eta }}} \right) + \end{array}}\\ \frac{{P\tilde c}}{p}({\omega _{\rm{1}}} + {\omega _2}) + \frac{{R\mathit{\Pi '}}}{{{c_p}p}}({\omega _{\rm{1}}} + {\omega _2}){\rm{ }}. \end{array} $

(51)

2.3.3 连续方程的三种形式

经过IAP变换后的微分和积分形式的连续方程如下：

$ {\frac{{\partial P}}{{\partial t}} + \frac{{\rm{1}}}{{{\rm{2}}P}}\left[ {\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\left({\frac{{\partial PU}}{{\partial \lambda }} + \frac{{\partial PV{\rm{sin}}\theta }}{{\partial \theta }}} \right) + \frac{{\partial \left({{P^{\rm{2}}}\dot \eta } \right)}}{{\partial \eta }}} \right] = {\rm{0}}}, $

(52)

$ {\frac{{\partial P}}{{\partial t}} = - \frac{{\rm{1}}}{{{\rm{2}}P}}\frac{{\rm{1}}}{{{\eta _s}}}\int {\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\left({\frac{{\partial PU}}{{\partial \lambda }} + \frac{{\partial PV{\rm{sin}}\theta }}{{\partial \theta }}} \right)\text{d}\eta } }, $

(53)

$ {{P^{\rm{2}}}\dot \eta = - \eta \frac{{\partial {P^{\rm{2}}}}}{{\partial t}} - \int {\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\left({\frac{{\partial PU}}{{\partial \lambda }} + \frac{{\partial PV{\rm{sin}}\theta }}{{\partial \theta }}} \right)\text{d}\eta } }. $

(54)

2.3.4 垂直速度定义

令

$ \left\{ \begin{array}{l} \mathit{\Theta '} = P\mathit{\Phi '}, \\ {\rm Z} = Pw, \end{array} \right. $

(55)

可得

$ \begin{array}{l} {{Z = \frac{{\rm{1}}}{g}\left[ {\frac{{\partial \mathit{\Theta '}}}{{\partial t}} + \frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\left({\frac{{\partial \mathit{\Theta '}u}}{{\partial \lambda }} - \frac{{\mathit{\Theta '}}}{{\rm{2}}}\frac{{\partial u}}{{\partial \lambda }}} \right) + } \right.}}\frac{{\rm{1}}}{{a{\rm{sin}}\theta }} \cdot \\ \left. {\left({\frac{{\partial \mathit{\Theta '}v{\rm{sin}}\theta }}{{\partial \theta }} - \frac{{\mathit{\Theta '}}}{{\rm{2}}}\frac{{\partial v{\rm{sin}}\theta }}{{\partial \theta }}} \right) + \frac{{\partial \mathit{\Theta '}\dot \eta }}{{\partial \eta }} - \frac{{\mathit{\Theta '}}}{{\rm{2}}}\frac{{\partial \dot \eta }}{{\partial \eta }} - {P^{\rm{3}}}\dot \eta \frac{{R\tilde T}}{p}} \right]. \end{array} $

(56)

2.3.5 高阶订正参数

令

$ H = P{\varepsilon }, $

(57)

可得

$ H=\frac{\text{1}}{g}\left[ \frac{\partial Z }{\partial t}+\frac{\text{1}}{a\text{sin}\theta }\left( \frac{\partial Z u}{\partial \lambda }-\frac{Z }{\text{2}}\frac{\partial u}{\partial \lambda } \right)+\frac{\text{1}}{a\text{sin}\theta }\cdot \right.\\ \left. {\left({\frac{{\partial { Z}v{\rm{sin}}\theta }}{{\partial \theta }} - \frac{{ Z}}{{\rm{2}}}\frac{{\partial v{\rm{sin}}\theta }}{{\partial \theta }}} \right) + \frac{{\partial { Z}\dot \eta }}{{\partial \eta }} - \frac{{ Z}}{{\rm{2}}}\frac{{\partial \dot \eta }}{{\partial \eta }}} \right]. $

(58)

2.3.6 其他方程

其他方程不受IAP变换影响，形式保持不变。一并列举如下：

气体状态方程：

$ {\alpha = \frac{{RT}}{p}}. $

(59)

静力平衡方程：

$ {\frac{{\partial \mathit{\Phi '}}}{{\partial \eta }} = - {P^{\rm{2}}}\frac{{RT'}}{p}.} $

(60)

第三运动方程：

$ {\frac{{\partial p}}{{\partial \mathit{\pi }}} = {\rm{1}} + \varepsilon }. $

(61)

垂直坐标定义：

$ \left\{ \begin{array}{l} \eta = \frac{{\pi - {\pi _\text{t}}}}{{{P^{\rm{2}}}}}, \\ {P^{\rm{2}}} = \frac{{{\pi _\text{s}} - {\pi _\text{t}}}}{{{\eta _\text{s}}}}. \end{array} \right. $

(62)

垂直方向边界条件：

$ {\dot \eta {|_{{\rm{ }}\eta = {\rm{0, }}{\eta _\text{s}}}} = {\rm{0}}}. $

(63)

经过上述推导，得到了非静力AREM动力方程组，采用适当方案对其进行时空离散后，就可以开展差分计算了。

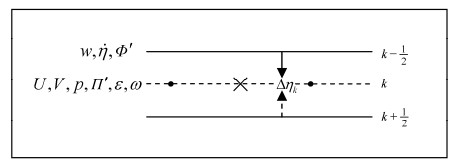
3 非静力方程组的时空离散 3.1 非静力框架的空间离散 3.1.1 变量空间分布及配置

非静力AREM模式进行空间离散时依然采用Arakawa-E网格分布形式和η坐标。在水平方向，除了水平风场（${U, {\rm{ }}V}$）分布在速度点（图 1中“·”），其余变量（${w, {\rm{ }}\dot \eta, {\rm{ }}\mathit{\Phi '}, {\rm{ }}p, {\rm{ }}\mathit{\Pi '}, {\rm{ }}\mathit{\varepsilon }}$）都分布在质量点（图 1中“×”）。图 1给出了变量的垂直分布形式。可以看出，变量在垂直方向采用Lorenz跳点分布，其中，${w, {\rm{ }}\mathit{\dot \eta }, {\rm{ }}\mathit{\Phi '}}$分布在界面层，而${U, {\rm{ }}V, {\rm{ }}p, {\rm{ }}\mathit{\Pi '}, {\rm{ }}\varepsilon, {\rm{ }}\mathit{\omega }}$分布在中间层。

3.1.2 同与静力平衡框架计算项的处理

从前述非静力方程组的推导及其与静力平衡方程组的比较（详见第5节）可以看出，非静力和静力平衡框架中有一些计算项是完全相同的，如水平平流、垂直平流、质量散度及坐标垂直速度的计算等。在选择相同网格分布和差分格式前提下，非静力框架中上述方程项的计算可以采用静力平衡框架的离散表达和处理方式（具体参见宇如聪，1992）。

3.1.3 不同于静力平衡框架计算项的处理

相比于静力平衡框架，非静力框架的第一、二运动方程中气压梯度力形式不同，而热力学能量方程中非平流项的处理存在差异；在本文中，我们将采用二阶精度的中央差分格式对它们进行离散计算。扰动静力平衡方程、扰动位势及垂直速度平流项的计算将参考静力平衡框架的处理方法实现。

3.2 非静力框架的时间分离及声波处理 3.2.1 时间分离技术

从前面的推导不难看出，热力学方程中定义了${\omega \alpha }$项（${\omega = \text{d}p/\text{d}t}, {p = p(x, y, \pi, t)}$），且$\omega $可以分解为${{\omega _{\rm{1}}} + {\omega _2}}$的形式，并具有如下性质：当${\varepsilon = {\rm{0}}}$时，${{\omega _{\rm{1}}} = \text{d}\pi /\text{d}t}$，表达为静力平衡的形式；而此时${{\omega _{\rm{2}}} = {\rm{0}}}$。这说明${{\omega _{\rm{2}}}}$与非静力平衡特性紧密相关，当取静力近似时，${{\omega _{\rm{2}}}}$便消失了，此时$\omega $仅由${{\omega _{\rm{1}}}}$决定。

通过上述分析说明，${{\omega _{\rm{1}}}}$和${{\omega _{\rm{2}}}}$具有不同的动力性质。如果对两者分别进行求解，不但物理意义明确，而且计算效率也能提高。正是根据这种计算思路，我们沿袭Janjic and Gerrity（2001）的做法，将热力学方程分解为两部分，即与平流项和${{\omega _{\rm{1}}}}$相关的第一分量${{{(\partial T/\partial t)}_{\rm{1}}} \leftarrow {\omega _{\rm{1}}} + \text{ADV}}$（ADV表示平流项），以及与${{\omega _{\rm{2}}}}$相关的第二分量$(\partial T/\partial t){_{\rm{2}} \leftarrow {\omega _{\rm{2}}}}$。再根据$\omega $、$w$、$\varepsilon $的定义及扰动静力平衡关系，对$p$、${\mathit{\Phi }'}$、w及$\varepsilon $的计算进行相应分离。

3.2.2 声波处理

通过分析发现温度、位势、垂直速度及高阶订正参数的第二分量方程共同组成了声波求解方程组。该方程组可通过消元法进行求解，即通过消元仅剩关于p的偏微分方程：

$ \begin{array}{l} R(1 - \kappa){P^{n + {1^2}}}\int_\eta ^{{\eta _s}} {\left({{{T'}_1} - \frac{{{{\tilde c}^2}}}{{(1 - \kappa)R}}} \right)\left({\frac{1}{{{p^{n + 1}}}} - \frac{1}{{{p_1}}}} \right)\text{d}\eta } = \\ {\left({g\Delta t} \right)^2}\left[ {\frac{1}{{{P^{n + {1^2}}}}}\frac{{\partial {p^{n + 1}}}}{{\partial \eta }} - (1 + {\varepsilon _1})} \right], \end{array} $

(64)

其中，$\kappa = R/{c_p}$，方程项包含下标“1”表示使用第一分量的时间积分结果，即对应“准静力”过程，而上标“n+1”表示整体时间积分结果，包含“非静力”过程。

我们定义$\frac{{\partial {p^*}}}{{\partial \eta }} \equiv {P^{n + {1^2}}}(1 + {\varepsilon _1})$，其中${p^*}$满足${p^*} = \pi {|_{\eta = 0}}$。将此定义带入（64）式，可得

$ \begin{array}{l} \frac{{R(1 - \kappa)}}{{{g^2}}}\int_\eta ^{{\eta _s}} {\left({{{T'}_1} - \frac{{{{\tilde c}^2}}}{{(1 - \kappa)R}}} \right)\left({\frac{{{P^{n + {1^2}}}}}{{{p^{n + 1}}}} - \frac{{{P^{n + {1^2}}}}}{{{p_1}}}} \right)\text{d}\eta } = \\ \Delta {t^2}\left[ {\frac{{\partial \left({\frac{{{p^{n + 1}}}}{{{P^{n + {1^2}}}}} - \frac{{{p^*}}}{{{P^{n + {1^2}}}}}} \right)}}{{\partial \eta }}} \right], \end{array} $

(65)

对上式进行$\frac{\partial }{{\partial \eta }}$运算，得

$ \begin{array}{l} - \frac{{R\left({1 - \kappa } \right)}}{{{g^2}}}\left({{{T'}_1} - \frac{{{{\tilde c}^2}}}{{(1 - \kappa)R}}} \right)\left({\frac{{{P^{n + {1^2}}}}}{{{p^{n + 1}}}} - \frac{{{P^{n + {1^2}}}}}{{{p_1}}}} \right) = \\ \Delta {t^2}\left[ {\frac{{{\partial ^2}\left({\frac{{{p^{n + 1}}}}{{{P^{n + {1^2}}}}} - \frac{{{p^*}}}{{{P^{n + {1^2}}}}}} \right)}}{{\partial {\eta ^2}}}} \right]. \end{array} $

(66)

通过引入符号$\mathit{\Psi } \equiv \frac{{{p^{n + 1}}}}{{{P^{n + {1^2}}}}}, $, ${\mathit{\Psi }^*} \equiv \frac{{{p^*}}}{{{P^{n + {1^2}}}}}, $, ${\mathit{\Psi }_1} \equiv \frac{{{p_1}}}{{{P^{n + {1^2}}}}}, $, $\mathit{\Gamma } \equiv \frac{{(1 - \kappa)R{{T'}_1} - {{\tilde c}^2}}}{{{{(g\Delta t)}^2}}}$，可将上式简化为

$ \frac{{{\partial ^2}(\mathit{\Psi } - {\mathit{\Psi }^*})}}{{\partial {\eta ^2}}} + \frac{{{\mathit{\Psi }_1} - \mathit{\Psi }}}{{\mathit{\Psi }{\mathit{\Psi }_1}}}\mathit{\Gamma } = 0. $

(67)

再定义$X \equiv \mathit{\Psi } - {\mathit{\Psi }^*}, D \equiv {\mathit{\Psi }_1} - {\mathit{\Psi }^*}$，得到：

$ \frac{{{\partial ^2}{\rm X}}}{{\partial {\eta ^2}}} - {\gamma ^2}{\rm X} = - {\gamma ^2}D. $

(68)

我们给定上边界固定，而下边界自由滑动，如下表达：

$ \left\{ \begin{array}{l} X{|_{\eta = 0}} = 0, \\ \frac{{\partial {\rm X}}}{{\partial \eta }}{|_{\eta = {\eta _\text{s}}}} = 0. \end{array} \right. $

(69)

该方程可以通过迭代法在上述边界条件[公式（69）]下得以求解。采用不等距差分格式对方程（68）进行离散：

$ \begin{array}{l} \frac{{\frac{{{X_{k + 1}} - {X_k}}}{{\Delta {\eta _k}}} - \frac{{{X_k} - {X_{k - 1}}}}{{\Delta {\eta _{k - 1}}}}}}{{\frac{1}{2}(\Delta {\eta _k} + \Delta {\eta _{k - 1}})}} - \frac{1}{4}(\gamma _{k + 1}^2{X_{k + 1}} + 2\gamma _k^2{X_k} + \gamma _{k - 1}^2{X_{k - 1}})\\ = - \frac{1}{4}\left({\gamma _{k + 1}^2{D_{k + 1}} + 2\gamma _k^2{D_k} + \gamma _{k - 1}^2{D_{k - 1}}} \right), \end{array} $

(70)

其中，$\Delta {\eta _k} = {\eta _{k + 1}} - {\eta _k}$。

令

$ \left\{ {\begin{array}{*{20}{l}} {{a_k} = \frac{2}{{\Delta {\eta _k}(\Delta {\eta _k} + \Delta {\eta _{k - 1}})}} - \frac{{\gamma _{k + 1}^2}}{4}, }\\ {{b_k} = \frac{2}{{\Delta {\eta _{k - 1}}\Delta {\eta _k}}} + \frac{{\gamma _k^2}}{2}, }\\ {{c_k} = \frac{2}{{\Delta {\eta _{k - 1}}(\Delta {\eta _k} + \Delta {\eta _{k - 1}})}} - \frac{{\gamma _{k - 1}^2}}{4}, }\\ {{d_k} = \frac{1}{4}\left({\gamma _{k + 1}^2{D_{k + 1}} + 2\gamma _k^2{D_k} + \gamma _{k - 1}^2{D_{k - 1}}} \right), } \end{array}} \right. $

(71)

则差分格式（70）简化为

$ {a_k}{X_{k + 1}} - {b_k}{X_k} + {c_k}{X_{k - 1}} = - {d_k}{\rm{, }}k = 1, {\rm{ }}2, {\rm{ }} \cdots, {\rm{ }}N - 1, $

(72)

边界条件离散为

$ {X_0} = 0, {\rm{ }}{X_N} = {X_{N - 1}}, $

(73)

联立（72）和（73）式即可利用追赶法求得气压方程的数值解。

3.2.3 时间积分方案

AREM是一个短期数值预报模式，因此其时间积分方案的选择主要考虑稳定性和计算效率两方面因素（宇如聪等，2004）。当前，AREM非静力框架时间积分方案的选择，仍沿用静力平衡框架的处理方法，对适应过程采用Mesinger（1977）的经济格式进行计算，而对于平流、扩散过程则选择简单的前差方案计算，声波通过追赶法和迭代法进行求解。

4 非静力框架计算实现 4.1 计算流程设计

非静力AREM积分流程的设计是以AREM静力平衡版本模式为基础，并借鉴了WRF-NMM模式的设计思想（Pyle et al., 2004）。在积分AREM非静力框架时，我们将遵循以下规则：

（1）初值和侧边界条件可满足静力平衡近似；

（2）模式运行第一步为静力平衡运行，并得到${w = \text{d}\mathit{\Phi }/(g\text{d}t)}$；

（3）模式运行第二步仍然为静力平衡运行，并得到${\varepsilon = \text{d}w/(g\text{d}t)}$；

（4）第三步以后，进行非静力计算。

4.2 非静力框架初始化及后处理

当然，要实现非静力模式完整、正常运行，还要具备初值处理和结果后处理功能。我们将继承AREM静力平衡模式初始化及后处理模块的相关处理方法（宇如聪等，2004），从而闭合非静力模式的计算过程，主要涉及物理常数与模式网格特性定义、地形数据处理、阶梯地形构造、标准层结扣除、模式变量IAP变换以及水平、垂直方向插值转换等功能。

5 非静力框架的静力平衡退化 5.1 第一运动方程

当${\varepsilon = }$时，静力平衡框架和非静力框架的第一运动方程在形式上只有一项不同，即：${(- \mathit{\Pi }'\tilde c/p) \cdot \partial p/(a{\rm{sin}}\theta \partial \lambda)}$，当取静力近似时，${p = \pi }$（全气压即静力气压），并令${S = (\pi - {\pi _t})/\pi }$，则有

$ {\begin{array}{l} - \frac{{\mathit{\Pi }'\tilde c}}{p}\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\frac{{\partial p}}{{\partial \lambda }} = - \frac{{\mathit{\Pi '}\tilde c}}{\pi }\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\frac{{\partial \pi }}{{\partial \lambda }} = - \frac{{\mathit{\Pi '}\tilde c}}{\pi } \cdot \\ {\rm{ }}\frac{{\pi - {\pi _\rm{t}}}}{{\pi - {\pi _\rm{t}}}}\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\frac{{\partial (\pi - {\pi _t})}}{{\partial \lambda }} = - \frac{{S\mathit{\Pi } '\tilde c}}{{\eta {P^2}}}\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\frac{{\partial (\eta {P^2})}}{{\partial \lambda }}\\ {\rm{ }} - \frac{{S\mathit{\Pi '}\tilde c}}{{{P^{\rm{2}}}}}\frac{{\rm{1}}}{{a{\rm{sin}}\theta }}\frac{{\partial {P^{\rm{2}}}}}{{\partial \lambda }} = - \frac{{S\tilde c\mathit{\Pi '}}}{{a{\rm{sin}}\theta }}\frac{{\partial ({\rm{ln}}{P^{\rm{2}}})}}{{\partial \lambda }}. \end{array}} = $

(74)

此时，非静力框架和静力平衡框架（参见宇如聪等（2004）第二章第18页2.68式）的第一运动方程完全一致。

5.2 第二运动方程

同理，对于第二运动方程，有

$ { - \frac{{\mathit{\Pi '}\tilde c}}{p}\frac{{\rm{1}}}{a}\frac{{\partial p}}{{\partial \theta }} = - \frac{{S\tilde c\mathit{\Pi '}}}{a}\frac{{\partial ({\rm{ln}}{P^{\rm{2}}})}}{{\partial \theta }}}. $

(75)

也可得到非静力框架和静力平衡框架（参见宇如聪等（2004）第二章第18页2.69式）的第二运动方程完全一致的结论。

5.3 热力学方程

通过比较发现静力平衡和非静力框架的热力学方程差别仅仅反映在非平流项上。对于静力平衡框架，此项表示为

$ {S\left({\tilde c + \frac{{R\mathit{\Pi }'}}{{{c_p}P}}} \right)\left({ - \frac{{\rm{1}}}{{P\eta }}\int {{D_{xy}}d\eta + U\frac{{\partial {\rm{ln}}{P^{\rm{2}}}}}{{a{\rm{sin}}\theta \partial \lambda }}} + V\frac{{\partial {\rm{ln}}{P^{\rm{2}}}}}{{a\partial \theta }}} \right)}. $

(76)

而非静力框架下，此项表示为

$ {\frac{{P\tilde c}}{p}\left({{\omega _{\rm{1}}} + {\omega _2}} \right) + \frac{{R\mathit{\Pi '}}}{{{c_p}p}}\left({{\omega _{\rm{1}}} + {\omega _2}} \right)}. $

(77)

当取静力近似时，可得

$ \begin{align} & \left(\frac{P\tilde{c}}{\pi }+\frac{R{{\mathit{\Pi }}^{'}}}{{{c}_{p}}\pi } \right)\left({{\omega }_{\text{1}}}+{{\omega }_{2}} \right)= \\ & \left(\frac{\pi -{{\pi }_\text{t}}}{\pi }\frac{P\tilde{c}}{\pi -{{\pi }_\text{t}}}+\frac{\pi -{{\pi }_\text{t}}}{\pi }\frac{\text{1}}{\pi -{{\pi }_\text{t}}}\frac{R{{\mathit{\Pi }}^{'}}}{{{c}_{p}}} \right)\left({{\omega }_{\text{1}}}+{{\omega }_{2}} \right)= \\ & \text{ }S\left(\tilde{c}+\frac{R{{\mathit{\Pi }}^{'}}}{{{c}_{p}}P} \right)\frac{{{\omega }_{\text{1}}}+{{\omega }_{2}}}{P\eta }. \\ \end{align} $

(78)

注意此时，${{\omega }_{\text{2}}}\equiv \text{0}$，$\varepsilon \equiv \text{0}$，且

$ P\eta \left(U\frac{\partial \text{ln}{{P}^{\text{2}}}}{a\text{sin}\theta \partial \lambda }+V\frac{\partial \text{ln}{{P}^{\text{2}}}}{a\partial \theta } \right), $

(79)

因此，

$ \begin{align} &\left(\frac{P\tilde{c}}{\pi }+\frac{R{\Pi }'}{{{c}_{p}}\pi } \right)\left({{\omega }_{1}}+{{\omega }_{2}} \right)=S\left(\tilde{c}+\frac{R{\Pi }'}{{{c}_{p}}P} \right)\frac{{{\omega }_{1}}+{{\omega }_{2}}}{P\eta }= \\ &\text{ }S\left(\tilde{c}+\frac{R{\Pi }'}{{{c}_{p}}P} \right)\left(-\frac{1}{P\eta }\int_{0}^{\eta }{\frac{1}{a\sin \theta }\left(\frac{\partial PU}{\partial \lambda }+\frac{\partial PV\sin \theta }{\partial \theta } \right)\cdot } \right. \\ &\text{ }\left. d\eta +U\frac{\partial \ln {{P}^{2}}}{a\sin \theta \partial \lambda }+V\frac{\partial \ln {{P}^{2}}}{a\partial \theta } \right). \\ \end{align} $

(80)

又由

$ {{D}_{xy}}=\frac{\text{1}}{a\text{sin}\theta }\left(\frac{\partial PU}{\partial \lambda }+\frac{\partial PV\text{sin}\theta }{\partial \theta } \right), $

(81)

所以，（80）式进一步写为

$ \begin{align} & \left(\frac{P\tilde{c}}{\pi }+\frac{R\mathit{{\Pi }'}}{{{c}_{p}}\pi } \right)\left({{\omega }_{\text{1}}}+{{\omega }_{2}} \right)=S\left(\tilde{c}+\frac{R\mathit{{\Pi }'}}{{{c}_{p}}P} \right)\cdot \\ & \left(-\frac{\text{1}}{P\eta }\int{{{D}_{xy}}\text{d}\eta +U\frac{\partial \text{ln}{{P}^{\text{2}}}}{a\text{sin}\theta \partial \lambda }}+V\frac{\partial \text{ln}{{P}^{\text{2}}}}{a\partial \theta } \right). \\ \end{align} $

(82)

此时，非静力框架和静力平衡框架[参见宇如聪等（2004）第二章第18页2.70式]的热力学方程完全一致。

5.4 静力平衡方程

当取静力近似时，$p=\pi $，所以，

$ \frac{\partial \mathit{{\Phi }'}}{\partial \eta }=-{{P}^{\text{2}}}\frac{R{T}'}{\pi }=-\frac{S\tilde{c}\mathit{{\Pi }'}}{P\eta }. $

(83)

此时，非静力框架与静力平衡框架（参见宇如聪等（2004）第二章第18页2.72式）下的扰动静力方程完全一致。

由前述，非静力框架与静力平衡框架下的连续方程、状态方程形式也完全一致，因此在$\varepsilon =\text{0}$时，非静力框架将退化为与原静力平衡框架一致的形式。这时通过简单的“$\varepsilon \left(\text{0, 1} \right)$开关”即可实现非静力与静力平衡框架的转换及比较。

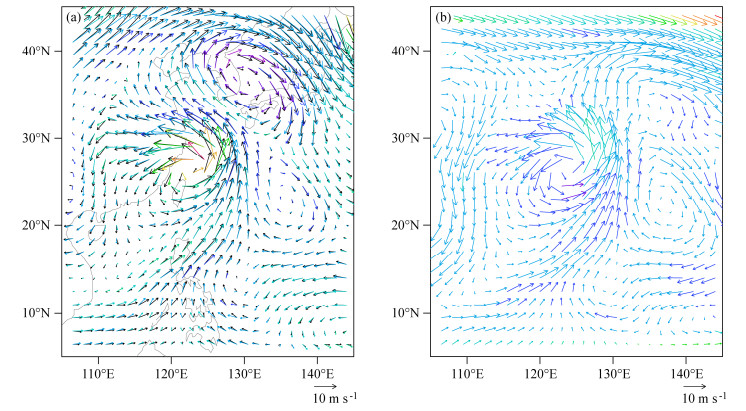
我们还设计了数值试验，来比较非静力框架退化为静力平衡框架后与原静力平衡框架模拟结果的差异。在此，模拟范围选为161×81×32，分辨率为37 km，积分24 h，不考虑地形和物理过程。对比模拟结果（图 2a）可以发现，两框架给出的流型和强度一致，微小的差别可能来自子程调用次序及数组计算精度的调整。同时，我们还比较了非静力框架的计算结果（图 2b），可以发现，静力和非静力框架模拟的低涡系统气旋式环流的分布相接近，同时低涡东部存在明显反气旋式环流；相比而言，非静力框架给出的反气旋环流中心位置更接近分析场，而且气旋中心强度更强。主要差别在低涡系统西北，静力平衡框架为反气旋式西南气流，而非静力框架则为反气旋式西北气流，分析场则显示存在着西北气流与西南气流的辐合。

6 总结与结论

AREM非静力框架的构造和程序实现充分考虑了原静力平衡框架的设计优势，也结合了国际上主流非静力模式设计的成功经验。主要有以下特点：

（1）该非静力框架是通过对静力平衡近似进行高阶松弛而建立的。与静力平衡框架相比，新发展的非静力框架主要区别在于完善了第三运动方程，定义了高阶订正参数和非静力连续方程。同时，水平动量方程中气压梯度力发生变化，热力学能量方程中非平流项发生变化。

（2）设计AREM非静力框架时仍然较好地使用了标准层结扣除和IAP变换，从而使静力平衡框架和非静力框架之间的转换与比较更加便利，并减小了由于两框架差别项过多而引起的计算困难。通过理论推导和模拟比对，可以发现：在静力近似下，AREM非静力框架退化为与原静力平衡框架一致的形式。

（3）AREM非静力框架依然基于$\eta $坐标和E网格进行空间离散，变量水平分布类似于静力平衡模式，但重新设计了变量的垂直交错分布形式。仍然采用具有二阶精度的中央差分形式进行空间离散，其中水平平流采用半格距差分形式。对于适应快过程采用Mesinger（1977）提出的经济格式，对于平流和扩散过程采用前差格式进行积分计算。

（4）基于对热力学方程非平流项的分析，采用时间两部离散技术进行积分计算从而可以单独求解声波，提高了模式运行效率。本文通过“追赶法”及迭代法对声波进行解算。

致谢 感谢已故中国科学院大气物理研究所周晓平研究员在AREM模式发展中给予的建议和帮助。