2 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室, 北京 100029
3 中国科学院大学, 北京 100049
4 中国科学技术大学地球和空间科学学院, 合肥 230026
5 中国科学院东亚区域气候-环境重点实验室, 北京 100029
2 State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics(LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
3 University of Chinese Academy of Sciences, Beijing 100049
4 School of Earth and Space Sciences(SESS), University of Science and Technology of China, Hefei 230016
5 Key Laboratory of Regional Climate?Environment for Temperate East Asia(TEA), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
数值模式和数值模拟是定量研究天气和气候变化的主要工具,但是由于数学模型中各变量之间复杂的非线性作用关系,导致模拟结果中存在着不确定性。政府间气候变化专门委员会报告中明确指出正确分析模式的不确定性是IPCC报告的主要任务之一(Mastrandrea et al., 2010)。这些不确定性的来源既包含物理参数的选取、模式的框架和观测的误差,也包括了计算误差的影响(Von Neumann and Goldstine, 1947)。计算误差对数值模拟结果的影响可以从复杂的大气环流模式(王鹏飞等, 2007)、耦合模式(陈显尧等, 2008)运行结果看出,也可以从简单的混沌动力系统(Li et al., 2000; Liao, 2009; Wang et al., 2014)、准地转模式(Teixeira et al., 2007)的数值试验得到验证。因此,如何采取有效的方法来控制计算误差的增长,对长时间的数值计算和精确的数值模拟至关重要。
大气和海洋流体力学模式中有许多形如
使用数值方法求解依赖于时间的常微分方程组或偏微分方程组时,主要是进行空间差分和时间积分两类计算。减小差分方法空间计算误差的途径有加大算法阶数和减小网格尺度两种,但是对于三维的复杂流体力学系统,算法阶数的增加往往是困难的。而网格尺度减小一半时,往往意味着计算量以24方式增加。在大气科学领域前人也进行了高阶算法的研究(季仲贞和王斌, 1994),高阶的差分格式往往存在一个问题,当计算精度提高了,其计算稳定性就降低了,季仲贞等(1999)使用守恒型的差分格式的办法,在计算精度和稳定性两方面取得了较好的平衡。高阶的空间差分算法有很多种实现,如紧致差分格式(Lele, 1992; Ma and Fu, 1996)已有一些应用。Li(2005)提出了一种空间导数的高阶计算方法,它的优点是采用显式计算,实现简单,而且省时,可以很方便的获得10阶甚至更高的阶数。冯涛和李建平(2007)利用此方法研究了一维平流方程、无粘Burgers方程(Hopf, 1950)、正压涡度方程的高精度差分格式,发现6阶空间差分算法的计算效果最好,而且增加的计算量并不多。但随着阶数的进一步增加,从7阶到10阶,计算结果改进的效果不明显,而且7阶以上的差分格式计算结果反而有变差的趋势。
减小时间积分计算误差也有两个途径:减小计算的时间步长和加大算法的阶数。缩小计算所用的时间步长是减小时间积分中误差的最简单方法,Li et al.(2000)和Teixeira et al.(2007)都对此做了研究,他们发现了计算结果对时间步长的敏感性。特别是获得混沌系统长时间数值解的方法不仅依赖于计算的步长,还与算法阶数和浮点计算精度有关。此外,还受制于实际消耗的计算时间,Wang et al.(2012)比较了4阶Runge-Kutta(RK)方法(简称RK4)和Taylor高阶算法在计算时间上的花费,结果表明:高阶算法能够将求解Lorenz方程花费的墙钟时间指数型的降低,高阶算法比使用最优步长计算的低阶算法更具效率。
上述分析表明通过增加算法阶数来减小时间积分时的计算误差是非常必要的。虽然冯涛和李建平(2007)利用Li(2005)方法进行了大量数值试验研究,但是他们的研究中存在两个问题,一是他们只在空间方向上使用了较高阶的算法,而时间积分上只采用了3阶左右的RK法,有可能使计算结果中的误差主要受时间积分误差的影响,从而导致算法不能取得更好的计算结果;二是求解时选取的初值出现不连续空间导数或出现空间导数无穷大等使用差分方法无法适用的问题,因而导致高阶精度算法无法获得比低阶精度算法更好的计算结果,这并不表示高阶精度算法对那些空间导数处处连续且有限的问题也无法提高计算的精度。
为了解决这些问题,Wang(2017)给出一类发展型偏微分方程的高阶Taylor-Li计算方案(简称TLW),它的特点是可以调节时间积分方案的阶数,完成从3阶到30阶甚至更高阶数的算法。Wang(2017)发现时间积分方案的阶数大于3之后,对应的最优空间差分精度阶数可以比6阶提高很多,这就解释了冯涛和李建平(2007)研究中6阶以上空间差分格式对结果无改进的现象,是由于没有使用足够高精度的时间积分方案引起的。
Wang(2017)的研究表明:当算法的时间积分阶数达到5时,一维线性平流方程的算例中相匹配的空间差分阶数为10阶,误差为10−6量级。而无粘Burgers的算例,与5阶时间积分相匹配的空间差分阶数为16阶,误差为10−14量级。因而,对于一些需要高精度,但又不要求极致的高精度解时,5、6阶的时间积分方案就够用了。相比于Taylor-Li算法,6阶以内的RK方法编程实现要简单,因此,本文将冯涛和李建平(2007)所用的RK3算法,改进为2~6阶可调的RK方法,配合Li高阶微分公式形成Runge-Kutta-Li(简称RKL)算法。通过多组数值试验,研究RKL方法中时间积分阶数对计算误差的影响,评估总体的计算性能,以期找到一种能够对复杂方程适用的简易高阶算法方案,当使用Taylor-Li算法编程代价过高时,替代Taylor-Li算法进行偏微分方程的高精度计算。
2 RK方法与Li空间差分算法联合的RKL算法 2.1 2~6阶RK与Li联合算法一维平流方程的形式为
| $\frac{{\partial u}}{{\partial t}} + \frac{{\partial u}}{{\partial x}} = 0$, | (1) |
其中,u为平流变量,可以用一个任意高阶精度的算法来求解。RK方法是一个经典的算法,常被用于求解常微分方程(ODEs),许多文献都对此方法如何微分方程系统进行了介绍(Hairer et al., 2000; Butcher, 2008)。
2阶RK方法如下:
| $\left\{ \begin{array}{l} {Z_1} = {z^n},\\ {Z_2} = {z^n} + \frac{1}{2}\tau f({Z_1}),\\ {Z^{n + 1}} = {z^n} + \tau f({Z_2}), \end{array} \right.$ | (2) |
3阶RK方法(Heun方法)如下:
| $\left\{ \begin{array}{l} {Z_1} = {z^n},\\ {Z_2} = {z^n} + \frac{1}{3}\tau f\left( {{Z_1}} \right),\\ {Z_3} = {z^n} + \frac{2}{3}\tau f\left( {{Z_2}} \right),\\ {Z^{n + 1}} = {z^n} + \frac{1}{4}\tau f\left( {{Z_1}} \right) + \frac{3}{4}\tau f\left( {{Z_3}} \right), \end{array} \right.$ | (3) |
4阶RK方法如下:
| $\left\{ \begin{array}{l} {Z_1} = {z^n},\\ {Z_2} = {z^n} + \frac{1}{2}\tau f\left( {{Z_1}} \right),\\ {Z_3} = {z^n} + \frac{1}{2}\tau f\left( {{Z_2}} \right),\\ {Z_4} = {z^n} + \tau f\left( {{Z_3}} \right),\\ {Z^{n + 1}} = {z^n} + \frac{1}{6}\tau \left[ {f\left( {{Z_1}} \right) + 2f\left( {{Z_2}} \right) + 2f\left( {{Z_3}} \right) + f\left( {{Z_4}} \right)} \right]. \end{array} \right.$ | (4) |
当RK算法阶数提升时,计算步数增加,方程的个数也增加明显,为了简便书写,可将其写为系数表的形式,例如RK4写成系数表的形式为
| $\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} 0\\ {\frac{1}{2}}\\ {\frac{1}{2}}\\ 1 \end{array}\left| {\underline {{\mkern 1mu} \begin{array}{*{20}{l}} {}&{}&{}&{}\\ {\frac{1}{2}}&{}&{}&{}\\ 0&{\frac{1}{2}}&{}&{}\\ 0&0&1&{} \end{array}{\mkern 1mu} } } \right.}\\ {\begin{array}{*{20}{c}} {\;\;\;\frac{1}{6}}&{\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{6}} \end{array}} \end{array}$ . | (5) |
其中,第1行表示:
5阶RK方法如下(Butcher, 2008;这里仅给出系数):
| $\begin{array}{r} \begin{array}{*{20}{c}} 0\\ {\frac{1}{4}}\\ {\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{1}{4}\begin{array}{*{20}{c}} {}\\ {} \end{array}}\\ {\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{1}{2}\begin{array}{*{20}{c}} {}\\ {} \end{array}}\\ {\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{3}{4}\begin{array}{*{20}{c}} {}\\ {} \end{array}}\\ {\begin{array}{*{20}{c}} {}\\ {} \end{array}1\begin{array}{*{20}{c}} {}\\ {} \end{array}} \end{array}\left| \!{\underline {{\mkern 1mu} {\begin{array}{*{20}{c}} {}&{}&{}&{}&{}&{}\\ {\frac{1}{4}}&{}&{}&{}&{}&{}\\ {\frac{1}{8}}&{\frac{1}{8}}&{}&{}&{}&{}\\ 0&0&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{1}{2}}&{}&{}&{}\\ {\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{3}{{16}}}&{ - \frac{3}{8}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{3}{8}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{9}{{16}}}&{}&{}\\ { - \frac{3}{7}}&{\frac{8}{7}}&{\frac{6}{7}}&{ - \frac{{12}}{7}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{8}{7}}&{\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {} \end{array}} \,}} \right. \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{7}{{90}}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}0}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{{32}}{{90}}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{{12}}{{90}}}&{\frac{{32}}{{90}}}&{\frac{7}{{90}}} \end{array} \end{array} $ . | (6) |
6阶RK方法如下(Butcher, 2008;这里仅给出系数):
| $\begin{array}{r} \begin{array}{*{20}{c}} 0\\ {\frac{1}{3}}\\ {\frac{2}{3}}\\ {\frac{1}{3}}\\ {\frac{5}{6}}\\ {\frac{1}{6}}\\ {\begin{array}{*{20}{c}} {}\\ {} \end{array}1\begin{array}{*{20}{c}} {}\\ {} \end{array}} \end{array}\left| \!{\underline {{\mkern 1mu} {\begin{array}{*{20}{c}} {}&{}&{}&{}&{}&{}&{}\\ {\frac{1}{3}}&{}&{}&{}&{}&{}&{}\\ 0&{\frac{2}{3}}&{}&{}&{}&{}&{}\\ {\frac{1}{{12}}}&{\frac{1}{3}}&{ - \frac{1}{{12}}}&{}&{}&{}&{}\\ {\frac{{25}}{{48}}}&{ - \frac{{55}}{{44}}}&{\frac{{35}}{{48}}}&{\frac{{15}}{8}}&{}&{}&{}\\ {\frac{3}{{20}}}&{ - \frac{{11}}{{24}}}&{ - \frac{1}{8}}&{\frac{1}{2}}&{\frac{1}{{10}}}&{}&{}\\ { - \frac{{261}}{{260}}}&{\frac{{33}}{{13}}}&{\frac{{43}}{{156}}}&{ - \frac{{118}}{{39}}}&{\frac{{32}}{{195}}}&{\frac{{80}}{{39}}\begin{array}{*{20}{c}} {}\\ {} \end{array}}&{} \end{array}\begin{array}{*{20}{c}} {} \end{array}} \,}} \right. \\ \begin{array}{*{20}{c}} {\frac{{13}}{{200}}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}0\begin{array}{*{20}{c}} {}\\ {} \end{array}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{{11}}{{40}}\begin{array}{*{20}{c}} {}\\ {} \end{array}\begin{array}{*{20}{c}} {}\\ {} \end{array}}&{\frac{{11}}{{40}}}&{\begin{array}{*{20}{c}} {}\\ {} \end{array}\frac{4}{{25}}}&{\frac{4}{{25}}}&{\frac{{13}}{{200}}} \end{array} \end{array}$ . | (7) |
需要注意的是,3阶以上的RK方法,系数形式并不唯一,这里选用了其中一种常用的形式。空间方向采用任意阶精度的Li算法(Li, 2005),计算公式为
| ${f_y}^{\left(m \right)}({y_i}) = \frac{1}{{{h^m}}}\sum\limits_{j = 0}^n {d_{n + 1, i, j}^{\left(m \right)}f({y_j})} $, | (8) |
其中,
当
当
| ${f_y}^{(1)}({y_i}) = \frac{1}{h}\sum\limits_{j = 0}^n {d_{n + 1, i, j}^{(1)}f({y_j})} $. | (9) |
计算时,空间导数的精度为n阶精度,为了保证空间导数能达到一定的精度,至少要求使用(n+1)个格点。例如取N=64,若n=5阶,则每次计算导数时需要6个格点,依此类推。具体的计算公式如下:
| $ d_{2,0,1}^{\left( 1 \right)} = 1,\;\;\;d_{2,1,0}^{\left( 1 \right)} = - 1, $ | (10) |
| $ d_{n + 1, i, j}^{(1)} = \frac{{{{(- 1)}^{(1 - j)}}a_{n - 1, i, j}^{(0)}}}{{j!(n - j)!}}, \;\;\;(当i \ne j) $ | (11) |
| $ d_{n + 1, i, i}^{(1)} = - \sum\limits_{j = 0, j \ne i}^n {d_{n + 1, i, j}^{(1)}}, \;\;(当i \ne j)$ | (12) |
| $ \begin{array}{l} a_{n - 1, i, j}^{\left(0 \right)} = {a_0}(- i, \cdots, k - i, \cdots, n - i), (k \ne i, k \ne j)\\ {\rm{ = }}(- i) \cdot (\cdots) \cdot (k - i) \cdot (\cdots) \cdot (n - i), (k \ne i, k \ne j) \end{array} $ | (13) |
存储空间的安排为
求解时每步中逐个格点先计算空间差,后使用RK法得到下一时刻的数值,全部格点计算完毕进入下一步积分,直到目标时刻,此即RKL方法对一维线性平流方程的求解过程。
2.2 RKL算法的多精度实现高阶算法在计算时还会碰到一个问题就是舍入误差,因为计算所用的时空精度阶数都可能超过10阶,Wang(2017)试验中,解的数值量级为
试验1:求解平流方程公式(1),使用Gauss波初始条件:
仿照(Takacs, 1985)的做法,定义总误差为
计算时x方向的空间步长为
|
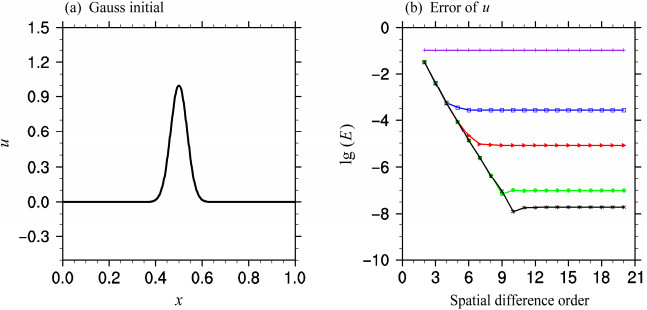
图 1 RKL(Runge-Kutta-Li)方法的线性平流试验:(a)Gauss波初始场;(b)计算误差随空间精度阶数的变化。(b)中横坐标为空间精度阶数,纵坐标为误差取对数(log10),粉、蓝、红、绿、黑色分别代表时间精度为2、3、4、5、6阶 Figure 1 The experiments of linear advection equation by RKL (Runge-Kutta-Li) method: (a) Gaussian-type initial condition; (b) error versus spatial difference order. In (b), the abscissa is the spatial difference order, the ordinate is the logarithm of the error (log10), and the purple, blue, red, green and black curves denote the second-order, third-order, fourth-order, fifth-order and sixth-order time-integration schemes, respectively |
对方波型初值也进行了试验[图略,与Wang(2017)的图 1相似],高阶精度(时间方向)算法只能获得和3阶精度差不多的结果。而对于光滑的初值(图 1),高阶RK算法可以取得较好的计算效果,基本上随着RK算法阶数的提升,Li微分方案对应的有效阶数也在加大,总误差在逐渐减小。产生这种差别的原因是方波型初值不连续,导致
作为非线性问题的示例,分析一维无粘性Burgers方程:
| $\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} = 0$. | (14) |
理论解的形式:如果初始场为
| $u(x, t) = f(x - u(x, t)t)$, | (15) |
一定是方程(14)的解,这可以通过如下关系式得到:
| $\frac{{\partial u}}{{\partial t}} = \frac{{ - uf'}}{{1 + tf'}}$, | (16) |
| $\frac{{\partial u}}{{\partial x}} = \frac{{f'}}{{1 + tf'}}$ . | (17) |
将方程(16)和(17)代入方程(14),可见等式成立。方程(16)和(17)可以用于检验程序中一阶数值微分的精确性,而通过公式(15),使用隐函数求解的办法,可以得到任意时刻的理论解,以对数值解进行评估。
试验2:求解无粘性Burgers方程
试验时,计算区域选为
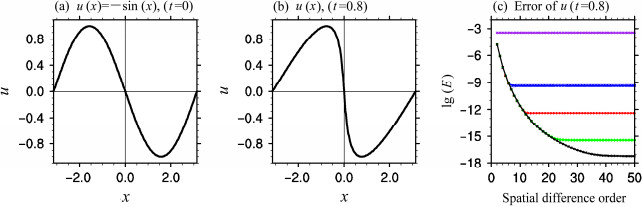
图 2给出了试验2的结果,由于计算时绝对误差会小于10−15,因此试验使用的是多精度的程序。从图 2c可以看出,在RK算法阶数为2时,计算误差较大,而且即使空间差分阶数提升,误差也无明显变化;当时间精度为3阶时,计算误差在空间精度达到6阶后就基本保持不变了;当时间精度为4、5、6阶时,有效的空间差分精度阶数分别可达12、25、40。这个试验说明了对非线性Burgers方程,只要时间积分精度阶数足够高,空间方向的差分精度阶数可以超过6阶。
|
图 2 RKL方法的无粘性Burgers方程试验:(a)t=0时的初始场;(b)t=0.8时u的理论解;(c)计算误差随空间精度阶数的变化。(c)中横坐标为空间精度阶数,纵坐标为误差取对数(log10),粉、蓝、红、绿、黑色分别代表时间精度为2、3、4、5、6阶 Figure 2 The experiments of the nonlinear Burgers' equation by RKL method: (a) Initial u at t=0; (b) analytical solution of u at t=0.8; (c) error versus spatial difference order. In (c), the abscissa is the spatial difference order and the ordinate is the logarithm of error (log10); purple, blue, red, green and black curves correspond to the second-order, third-order, fourth-order, fifth-order and sixth-order time-integration schemes, respectively |
对另外一组初值
综上所述,对于非线性无粘Burgers方程,高阶精度算法能否获得好的计算结果,除了受初值场分布形势的影响,还与计算的目标时刻有联系。当解的各阶导数连续且未出现
值得一提的是,若数值解能够具有周期边界条件,求解精度会比非周期边界条件的高,这主要是周期边界条件满足时,总可以将目标格点放置于差分公式中的中点附近,计算时误差小。而非周期的边界条件,在边界点以及紧靠边界点处,即使能够用n阶精度的差分格式,目标格点也会被放置于偏离n个差分点中心的位置,实际计算表明这些位置的差分精度较差。
5 结论本文利用Li提出的高阶显式微分公式,结合Runge-Kutta时间积分方案,实现了求解含时偏微分方程的Runge-Kutta-Li高阶算法格式。对一维平流方程,通过比较理论解和各阶计算格式的数值解,研究了计算误差随时间积分阶数的变化情况。结果表明:对于一些光滑、周期边界条件的初值,如果时间方向的积分精度为3阶,计算误差在空间差分阶数到达6阶后减小的不明显。而当时间积分的阶数大于3,例如选为4、5、6阶时,此时空间差分阶数超过6之后,计算误差仍有减小的趋势,相应的有效空间差分阶数可以超过6阶,说明了冯涛等所发现的计算误差在空间差分精度达到6阶出现饱和的现象是由于没有足够高的时间积分方案配合而引起的。对于方波这样的初值,本文计算结果与以前的研究一致。
对非线性的Burgers方程,一个光滑的且满足周期边界条件的算例表明,Runge-Kutta-Li格式能够取得较好的计算效果。相比于冯涛和李建平(2007)使用的3阶时间积分方案,本文实现了2~6阶的RK时间积分算法,而相应的空间差分精度也能从6阶拓展到30阶以上,因而计算精度也极大提升。
虽然可以通过减小时间步长来改进时间积分的精度,但是它的效率不如增加阶数高,这在以往的研究中已经被论证(Wang et al., 2012)。因此,相比于以往的仅增加空间差分精度的高阶算法,本文在时空两个方向提高算法的精度阶数,减少了总体计算误差。为了控制高阶算法计算过程中浮点舍入误差的影响,使用多精度计算的工具库,实现了可以求解平流方程和Burgers方程的RKL格式,此方法可以方便的拓展到其它类似方程的求解中。
本文实现的RKL算法程序可以灵活的指定时间积分阶数(2~6阶)、空间计算的阶数,还能够方便的调整空间格距、时间积分的步长,因此适用于研究算法阶数、时空步长和计算误差之间的复杂关系。本研究仅用到最高6阶RK方法,对于6阶以上的RK方法,实现较为复杂,特别是RK方法中的系数计算公式,若用到MP库计算则必须为完全准确的(即不能查算好的系数表,要在程序里自己算),因而会增加程序实现的困难,有兴趣的研究者可以仿照本文方法,进行更高阶数的试验。
Butcher J C. 2008. Numerical Methods for Ordinary Differential Equations[M]. 2nd ed. England: John Wiley & Sons: 463pp.
|
陈显尧, 宋振亚, 赵伟, 等. 2008. 气候模式系统模拟结果的不确定性分析[J]. 海洋科学进展, 26(2): 119-125. Chen Xianyao, Song Zhenya, Zhao Wei, et al. 2008. Uncertainity analysis of results simulated by climate model system[J]. Advances in Marine Science (in Chinese), 26(2): 119-125. DOI:10.3969/j.issn.1671-6647.2008.02.001
|
冯涛, 李建平. 2007. 高精度迎风偏斜格式的比较与分析[J]. 大气科学, 31(2): 245-253. Feng Tao, Li Jianping. 2007. A comparison and analysis of high order upwind-biased schemes[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 31(2): 245-253. DOI:10.3878/j.issn.1006-9895.2007.02.06
|
Hairer E, Nørsett S P, Wanner G. 2000. Solving Ordinary Differential Equations I:Nonstiff Problems[M]. Berlin Heidelberg: Springer: 528pp.
|
Hopf E. 1950. The partial differential equation ut + uux=μxx[J]. Commun. Pure Appl. Math., 3(3): 201-230. DOI:10.1002/cpa.3160030302
|
季仲贞, 王斌. 1994. 一类高时间差分精度的平方守恒格式的构造及其应用检验[J]. 自然科学进展, 4(2): 149-157. Ji Zhongzhen, Wang Bin. 1994. Construction and application test of a kind of high precision scheme with square-conservation[J]. Progress in Natural Science (in Chinese), 4(2): 149-157. DOI:10.3321/j.issn:1002-008X.1994.02.004
|
季仲贞, 李京, 王斌. 1999. 紧致平方守恒格式的构造和检验[J]. 大气科学, 23(3): 323-332. Ji Zhongzhen, Li Jing, Wang Bin. 1999. Construction and test of compact scheme with square-conservation[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 23(3): 323-332. DOI:10.3878/j.issn.1006-9895.1999.03.08
|
Lele S K. 1992. Compact finite difference schemes with spectral-like resolution[J]. J. Comput. Phys., 103(1): 16-42. DOI:10.1016/0021-9991(92)90324-R
|
Li J P. 2005. General explicit difference formulas for numerical differentiation[J]. J. Comput. Appl. Math., 183(1): 29-52. DOI:10.1016/j.cam.2004.12.026
|
Li J P, Zeng Q C, Chou J F. 2000. Computational uncertainty principle in nonlinear ordinary differential equations (I)——Numerical results[J]. Science in China (Series E), 43(5): 449-460.
|
Liao S J. 2009. On the reliability of computed chaotic solutions of non-linear differential equations[J]. Tellus A, 61(4): 550-564. DOI:10.1111/j.1600-0870.2009.00402.x
|
Ma Y W, Fu D X. 1996. Super compact finite difference method (SCFDM) with arbitrary high accuracy[J]. Comput. Fluid Dyn. J., 5(2): 259-276.
|
Mastrandrea M D, Field C B, Stocker T F, et al. 2010. Guidance Note for Lead Authors of the IPCC Fifth Assessment Report on Consistent Treatment of Uncertainties[C]. Jasper Ridge, CA, USA: Intergovernmental Panel on Climate Change.
|
Takacs L L. 1985. A two-step scheme for the advection equation with minimized dissipation and dispersion errors[J]. Mon. Wea. Rev., 113(6): 1050-1065. DOI:10.1175/1520-0493(1985)113<1050:ATSSFT>2.0.CO;2
|
Tal-Ezer H. 1986. Spectral methods in time for hyperbolic equations[J]. SIAM J. Numer. Anal., 23(1): 11-26. DOI:10.1137/0723002
|
Tal-Ezer H. 1989. Spectral methods in time for parabolic problems[J]. SIAM J. Numer. Anal., 26(1): 1-11. DOI:10.1137/0726001
|
Teixeira J, Reynolds C A, Judd K. 2007. Time step sensitivity of nonlinear atmospheric models:Numerical convergence, truncation error growth, and ensemble design[J]. J. Atmos. Sci., 64(1): 175-189. DOI:10.1175/JAS3824.1
|
Von Neumann J, Goldstine H H. 1947. Numerical inverting of matrices of high order[J]. Bull. Amer. Math. Soc., 53(11): 1021-1099. DOI:10.1090/S0002-9904-1947-08909-6
|
Wang P F. 2017. A high-order spatiotemporal precision-matching Taylor-Li scheme for time-dependent problems[J]. Adv. Atmos. Sci., 34(12): 1461-1471. DOI:10.1007/s00376-017-7018-1
|
王鹏飞, 王在志, 黄刚. 2007. 舍入误差对大气环流模式模拟结果的影响[J]. 大气科学, 31(5): 815-825. Wang Pengfei, Wang Zaizhi, Huang Gang. 2007. The influence of round-off error on the atmospheric general circulation model[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 31(5): 815-825. DOI:10.3878/j.issn.1006-9895.2007.05.06
|
Wang P F, Li J P, Li Q. 2012. Computational uncertainty and the application of a high-performance multiple precision scheme to obtaining the correct reference solution of Lorenz equations[J]. Numerical Algorithms, 59(1): 147-159. DOI:10.1007/s11075-011-9481-6
|
Wang P F, Liu Y, Li J P. 2014. Clean numerical simulation for some chaotic systems using the parallel multiple-precision Taylor scheme[J]. Chinese Sci. Bull., 59(33): 4465-4472. DOI:10.1007/s11434-014-0412-5
|
吴声昌, 刘小清. 1996. KdV方程的时间谱离散方法[J]. 应用数学和力学, 17(4): 357-362. Wu Shengchang, Liu Xiaoqing. 1996. Spectral method in time for KdV equations[J]. Applied Mathematics and Mechanics (in Chinese), 17(4): 357-362.
|
 2019, Vol. 43
2019, Vol. 43

