2 高原与盆地暴雨旱涝灾害四川省重点实验室, 成都 610072
3 四川省内江市气象局, 四川内江 641000
4 南京信息工程大学, 南京 210044
5 四川省气象服务中心, 成都 610072
2 Heavy Rain and Drought-Flood Disasters in Plateau and Basin Key Laboratory of Sichuan Province, Chengdu 610072
3 Neijiang Meteorological Bureau, Neijiang, Sichuan Province 641000
4 Nanjing University of Information Science & Technology, Nanjing 210044
5 Sichuan Meteorological Service Center, Chengdu 610072
1990年代以来,北半球冬季许多地区如美国、中国和欧洲等地都频繁出现了极端严寒的天气与气候,并伴随着强烈的风暴与暴风雪以及破纪录的冰冻雨雪事件。一些研究表明,北极增暖使得北极与中纬度地区间的厚度梯度和温度梯度减小,导致中高纬地区冬季西风急流减弱,大尺度行星波发展,经向活动增强,有利于北极地区冷空气向南侵袭,引发中纬度地区低温事件出现(Francis et al., 2009; Overland and Wang, 2010; Francis and Vavrus, 2012; Ding et al., 2014, 2017)。在西风急流低层,冬季西风急流减弱到一定程度,将出现断裂现象。而这种断裂的情形,从几何意义上来说,是发生了分岔现象,表征着西风带结构发生了变化。
1939年,Rossby首先提出了西风带环流指数的概念;之后Namias(1950)就实际天气过程概述了西风带高低指数的循环过程。大气西风带环流低指数状态是纬向气流弱,行星波振幅大;而西风带环流高指数状态是纬向气流强,行星波振幅小,实际大气中西风带高低指数循环约为2~6周的时间(Charney and DeVore, 1979;金飞飞和朱抱真,1986a)。国际上很多学者(Lorenz,1972; Hoskin and Hollingsworth, 1973; Gill, 1974; Deininger, 1982; Simmons et al., 1983)对西风环流的形成开展了卓有成效的研究,尤其是有限振幅波的发现,突破了以往小扰动线性理论的束缚,为西风环流不稳定发展的研究奠定了基础。叶笃正等(1958)将经向环流建立的动力原因归结为斜压不稳定。曾庆存等(1979)认为纬向环流的建立过程是大气的旋转适应过程。这些结果均对理解西风环流变化的本质具有重要意义,然而,对于西风带高低指数环流之间的转换过程,目前研究的还不是很多。
关于西风带高低指数循环的研究,Charney and DeVore(1979)把准地转β平面近似的正压模式的双稳态与大气中高低西风带指数联系起来,并且指出地形和热力强迫波引起的一类低指数达到稳定平衡态是大气阻塞现象的原因。Charney and Straus(1980)发现,在斜压模式中,高指数的平衡态是不稳定的,只有一类低指数的平衡态是稳定的。他们还通过数值计算发现,可以用平衡态不稳定来解释移动性行星波构成周期性振荡的过程。然而,他们并未研究高低指数平衡态之间的转换。Mitchell and Dutton(1981)指出在正压强迫模式中平衡态不稳定的周期解是一种恒幅行波,从而得到了一种最简单的振荡,并发现了一类既有定常的强迫运动,又有移动性的自由波运动的混合型环流,可以表示持续性准定常的阻塞形势。金飞飞和朱抱真(1986b)利用两层准地转低阶模式研究了强迫波、自由波与纬向气流的共振作用,解释了高低指数特征流型的维持和转换。这些结果从动力学的角度解释了西风带高低指数的维持和转换,为后来的数值模拟奠定了理论基础。
然而,以上这些研究更多的是关于截断模式中涡度系数随时间变化的稳定性。虽然涡度系数的稳定性对流型的转换有重要作用,但西风带高低指数环流之间的相互转换,实际上是环流在空间结构上的变化,因此,还需在分析涡度系数随时间变化的稳定性的基础上,进一步将涡度系数与表征流型的基函数结合起来,讨论流型的空间结构变化,以及涡度系数的稳定性对空间结构的影响。为此,将气象上常用的等值线通过切线的方式,转化为二维空间上的向量方程,探讨流型等值线的结构变化,获得与等值线分析方法一致的结果,并能将数值模拟和动力分析紧密的结合在一起。这一方法,目前在气象上仍鲜见应用。
对于影响流型转换机制的因子,除了地球自转引起的纬向环流以外,由β效应引起的经向风速切变带来的切变动量的传递,南北温度梯度引起位能转换的动量水平涡动输送是影响西风带变化的主要因素(王为德,1983)。为了研究在维持西风带高低指数循环的过程中,大气内部所应具有的动力作用,直接采用三角函数来表示水平涡动输送,而不讨论位能的转换及地形、热源等外源强迫的作用。流型转换过程中,当大气西风带处于低指数状态时,纬向气流弱,往往容易产生纬向环流断裂的情况(王为德,1983;罗德海,2001)。分析发现,只有扰动是不会出现纬向环流断裂现象。为此,需进一步分析波流相互作用对这一异常现象的影响。而大气环流带断裂的现象,从几何的角度上看,是由于大气的空间结构发生了变化,这种变化往往伴随着分岔现象(朱抱真等,1991),为此,本文将采用分岔的方法来研究纬向环流断裂这种异常现象。本文首先利用准地转正压涡度方程,得到正压模式流函数的等值线和向量形式,再结合涡度系数周期性变化,研究西风带流函数的空间结构变化,然后分析波流相互作用对纬向环流断裂的影响。最后给出本文的主要结论,并对这些结论可能存在的异议进行了讨论。
2 方法由于球坐标系中方程的形式复杂,因此,除了考虑全球范围内的大气运动时必须采用球坐标系外,通常都采用局地直角坐标系(吕美仲等,2004)。由于本研究集中在北半球西风带,为此,文章采用局地直角坐标系下的无热源和无地形的β平面近似的准地转正压涡度方程(Hoskins and Hollingsworth, 1973):
| $\frac{\partial }{{\partial t}}{\nabla ^2}\psi + \beta \frac{{\partial \psi }}{{\partial x}} + J(\psi, {\nabla ^2}\psi) = 0, $ | (1) |
来分析北极与中纬度及副热带能量相互输送的机制,其中,
| $J(\psi, {\nabla ^2}\psi) = \frac{{\partial \psi }}{{\partial x}}\frac{{\partial {\nabla ^2}\psi }}{{\partial y}} - \frac{{\partial \psi }}{{\partial y}}\frac{{\partial {\nabla ^2}\psi }}{{\partial x}}, $ | (2) |
而
| $\psi = \bar \psi + \psi '.$ | (3) |
同时,Hoskins and Hollingsworth(1973)认为,大气环流基本流是纬向不均匀的Rossby波。为此,将基本流
| $\bar \psi = - Uy + A\sin {k_0}(x - ct), $ | (4) |
其中,U为平均纬向风速,
| $\frac{\partial }{{\partial t}}{\nabla ^2}\psi ' + U\frac{{\partial {\nabla ^2}\psi '}}{{\partial x}} + \beta \frac{{\partial \psi '}}{{\partial x}} + \\ {k_0}A\cos {k_0}(x - ct)\left({\frac{{\partial {\nabla ^2}\psi '}}{{\partial y}} + k_0^2\frac{{\partial \psi '}}{{\partial y}}} \right) = 0.$ | (5) |
由于基本流
| $x' = x - ct.$ | (6) |
在新坐标系下,将基本流
| $\frac{\partial }{{\partial t}}{\nabla ^2}\psi ' + \left({\frac{\beta }{{k_0^2}}\frac{\partial }{{\partial x}} + {k_0}A\cos ({k_0}x)\frac{\partial }{{\partial y}}} \right)({\nabla ^2}\psi ' + k_0^2\psi ') = 0.$ | (7) |
方程(7)不容易求得精确解,采用如下方式对其近似计算:对函数
| ${\nabla ^2}\psi ' = {\psi '_B}\cos {l_1}y + {\psi '_C}\sin {l_1}y\sin ({k_0}x + \theta), $ | (8) |
其中,涡度系数
| $\psi ' = \frac{{{{\psi '}_B}}}{{l_1^2}}\cos {l_1}y + \frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\cos {k_0}x, $ | (9) |
其中,公式右侧第一项为对平均纬向气流的纬向不均匀扰动;公式右侧第二项为经向扰动,表征动量的水平涡动输送,由经圈环流引起的位能转换得到(王为德,1983)。
将公式(4)和(9)带入到公式(3)中,则有正压模式西风流函数表达式:
| $\psi = - Uy + A\sin {k_0}x + \frac{{{{\psi '}_B}}}{{l_1^2}}\cos {l_1}y + \frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\cos {k_0}x.$ | (10) |
下面,将利用公式(10),分析平均纬向气流
| 表 1 本文使用的假设条件的理由及可能存在的问题 Table 1 Reasons for the assumptions and possible problems used in this article |
为了分析平均纬向气流
| $\psi \equiv - Uy + A\sin {k_0}x + \frac{{{{\psi '}_B}}}{{l_1^2}}\cos {l_1}y + \\ \ \ \ \ \ \ \ \ \frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\cos {k_0}x = {\psi _0}, $ | (11) |
其中,
| $\frac{{\partial \psi }}{{\partial x}}{\text{d}}x + \frac{{\partial \psi }}{{\partial y}}{\text{d}}y = 0.$ | (12) |
由于
| $\frac{{{\text{d}}y}}{{{\text{d}}x}} = - \frac{{{{(\psi)}_x}}}{{{{(\psi)}_y}}} = - \frac{{A{k_0}\cos {k_0}x - {k_0}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\sin {k_0}x}}{{ - U - \frac{{{{\psi '}_B}}}{{{l_1}}}\sin {l_1}y + {l_1}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\cos {l_1}y\cos {k_0}x}}.$ | (13) |
由于
| $\begin{gathered} \left\{ \begin{gathered} \frac{{{\text{d}}x}}{{{\text{d}}t}} = U + \frac{{{{\psi '}_B}}}{{{l_1}}}\sin {l_1}y - {l_1}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\cos {l_1}y\cos {k_0}x, \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}t}} = A{k_0}\cos {k_0}x - {k_0}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\sin {k_0}x. \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \end{gathered} $ | (14) |
方程(14)的第二式除以第一式,为切线方程(13),故二维方程(14)的相轨线可以表示流函数等值线的切线向量。方程(14)的右边各项中,既有时间变量的涡度系数,也有空间变量的三角函数,但二者之间是相互独立的。因此,下面将不同时刻的扰动涡度系数看成参数,分别对基本流满足
根据上面的分析,本节首先讨论基本流
| $\left\{ \begin{array}{l} \frac{{{\text{d}}x}}{{{\text{d}}t}} = \frac{{{{\psi '}_B}}}{{{l_1}}}\sin {l_1}y - {l_1}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\cos {l_1}y\cos {k_0}x, \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}t}} = - {k_0}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\sin {k_0}x. \hfill \\ \end{array} \right.$ | (15) |
为了研究扰动方程(15)的几何结构,利用微分方程的稳定性来进行分析。首先,求方程(15)的平衡点,令(15)式右边等于零(Charney and DeVore, 1979;张锦炎,1981),计算得到对应的平衡点为
| $\left({\frac{m}{{2{k_0}}}{\rm{ \mathsf{ π} }}, \frac{n}{{{l_1}}}\pi } \right), {\text{ }}\left({\frac{m}{{{k_0}}}{\rm{ \mathsf{ π} }}, {\text{ arctg}}\left({\frac{{l_1^2}}{{l_1^2 + k_0^2}}\frac{{{\psi _C}^\prime }}{{{\psi _B}^\prime }}} \right)} \right).\\ m = 0, {\text{ }} \pm 1, {\text{ }} \pm 2 \cdots, n = 0, {\text{ }} \pm 1, {\text{ }} \pm 2 \cdots $ | (16) |
其次,通过分析平衡点处的特征值来获得扰动方程的几何结构。
(Ⅰ)对于平衡点
| ${\lambda ^2} - {\left({\frac{{{l_1}{k_0}}}{{l_1^2 + k_0^2}}{\psi _C}^\prime } \right)^2} = 0, $ | (17) |
特征方程有一正一负两实根,此时平衡点为鞍点。
(Ⅱ)对于平衡点
| ${\lambda ^2} + \frac{{l_1^2k_0^2({\psi _B}{{^\prime }^2} + {\psi _C}{{^\prime }^2})}}{{{{(l_1^2 + k_0^2)}^2}}}{\sin ^2}\vartheta = 0, $ | (18) |
其中,
| $\vartheta = {\text{arctg}}\left({\frac{{l_1^2}}{{l_1^2 + k_0^2}}\frac{{{\psi _C}^\prime }}{{{\psi _B}^\prime }}} \right), $ | (19) |
此时,特征方程有一对共轭纯虚根,此时平衡点为中心。从平衡点的表达式可以看出,中心的纵坐标
上面的讨论,是将扰动涡度系数
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{{\psi '}_B}}}{{{\rm{d}}t}} = - \frac{1}{2}{k_0}{l_1}{g_0}A{{\psi '}_C}, \\ \frac{{{\rm{d}}{{\psi '}_C}}}{{{\rm{d}}t}} = {k_0}{l_1}{g_1}A{{\psi '}_B}, \end{array} \right. $ | (20) |
其中,
| ${g_0} = 1 - \frac{{k_0^2}}{{k_0^2 + l_1^2}}, {g_1} = 1 - \frac{{k_0^2}}{{l_1^2}}, $ | (21) |
则方程(20)前两式对应的特征方程为
| ${\lambda ^2} + \frac{1}{2}l_1^2k_0^2{A^2}{g_0}{g_1} = 0.$ | (22) |
由于l1、k0、A均不为零,而
(Ⅰ)当
(Ⅱ)当
在实际大气运动中,扰动波数往往是大于基波波数(朱抱真等,1991),即
| $\frac{{{\text{d}}{{\psi '}_C}}}{{{\text{d}}{{\psi '}_B}}} = - \frac{{2{g_1}{{\psi '}_B}}}{{{g_0}{{\psi '}_C}}}, $ | (23) |
可以解得
| $ 2{g_1}\psi _B^{'2} + {g_0}\psi _C^{'2} = r_0^2. $ | (24) |
其中,
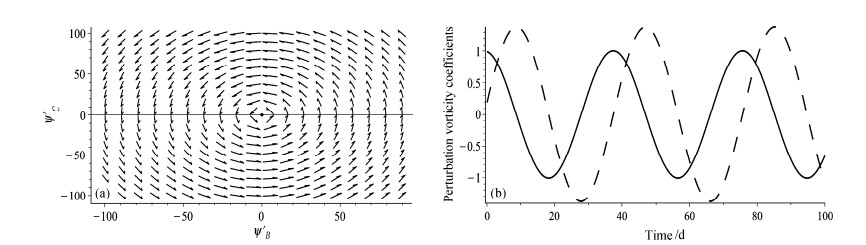
|
图 1 扰动涡度系数 |
进一步,对方程(20)的第一式微分,并将第二式代入第一式,得到关于
| $\frac{{{{\text{d}}^2}{{\psi '}_B}}}{{{\text{d}}{t^2}}} + {\omega ^2}{\psi '_B} = 0, $ | (25) |
其中,
| ${\omega ^2} = \frac{1}{2}l_1^2k_0^2{g_0}{g_1}{A^2}, $ | (26) |
| ${\psi '_B} = {A_B}\sin (\omega t + \phi), $ | (27) |
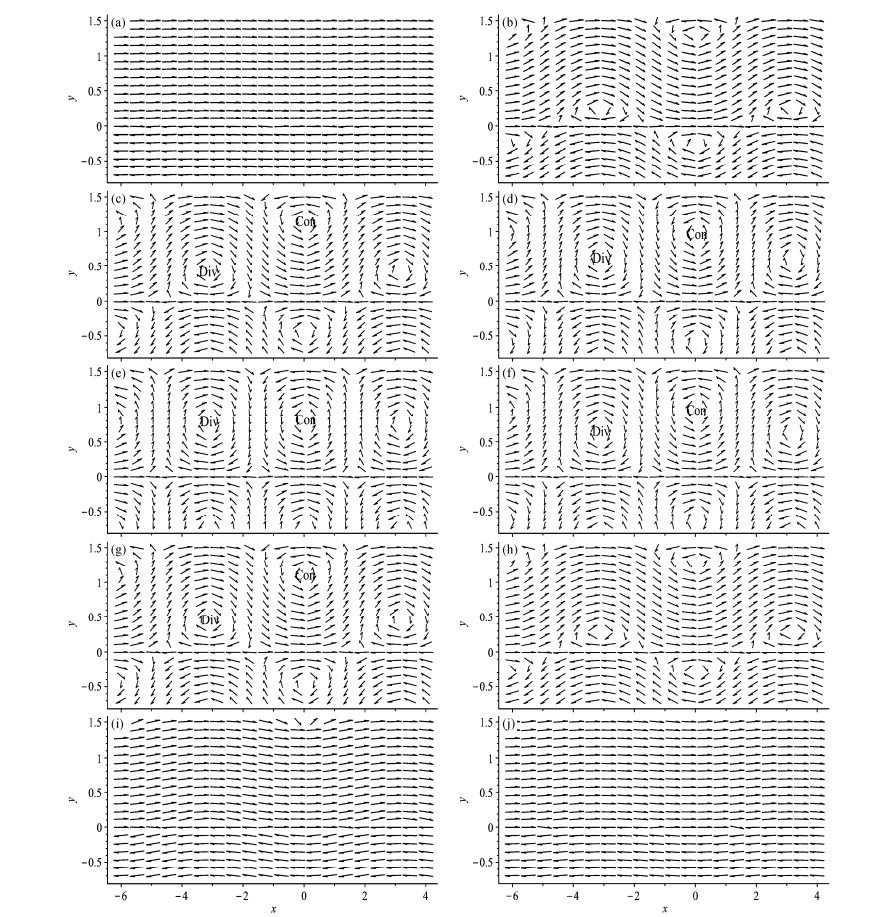
|
图 2 一个周期内的扰动环流 |
在只有扰动流作用下,西风带大气运动主要分两个阶段。在第一阶段,水平涡动输送
上述分析揭示:当基本流
上节讨论了基本流
| $\frac{{{\text{d}}{\boldsymbol{x}}}}{{{\text{d}}t}} = {\boldsymbol{G}}({\boldsymbol{x}}, \mathit{\boldsymbol{\alpha }}), $ | (28) |
其中,
| $\left\{ \begin{array}{l} \det [J({\boldsymbol{x}}, \mathit{\boldsymbol{\alpha }})] = 0, \hfill \\ {\boldsymbol{G}}({\boldsymbol{x}}, \mathit{\boldsymbol{\alpha }}) = 0, \hfill \\ \end{array} \right.$ | (29) |
其中,det(A)表示求矩阵A的行列式;
| $\left\{ \begin{array}{l} {G_1}(x, y) = U + \frac{{{{\psi '}_B}}}{{{l_1}}}\sin {l_1}y - {l_1}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\cos {l_1}y\cos {k_0}x, \hfill \\ {G_2}(x, y) = A{k_0}\cos {k_0}x - {k_0}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\sin {k_0}x. \hfill \\ \end{array} \right.$ | (30) |
| $ J({\boldsymbol{x}}, {\bf{\mathit{\boldsymbol{ \alpha }} }}) = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {G_1}}}{{\partial x}}}&{\frac{{\partial {G_1}}}{{\partial y}}}\\ {\frac{{\partial {G_2}}}{{\partial x}}}&{\frac{{\partial {G_2}}}{{\partial y}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{{l_1}{k_0}{{\psi '}_C}}}{{l_1^2 + k_0^2}}\cos {l_1}y\sin {k_0}x}&{{{\psi '}_B}\cos {l_1}y + \frac{{l_1^2{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\cos {k_0}x}\\ { - Ak_0^2\sin {k_0}x - \frac{{k_0^2{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}y\cos {k_0}x}&{ - \frac{{{l_1}{k_0}{{\psi '}_C}}}{{l_1^2 + k_0^2}}\cos {l_1}y\sin {k_0}x} \end{array}} \right]. $ | (31) |
根据方程(29),得到关于方程(14)分岔点
| $\left\{ \begin{array}{l} U + \frac{{{{\psi '}_B}}}{{{l_1}}}\sin {l_1}\bar y - {l_1}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\cos {l_1}\bar y\cos {k_0}\bar x = 0, \hfill \\ A{k_0}\cos {k_0}\bar x - {k_0}\frac{{{{\psi '}_C}}}{{l_1^2 + k_0^2}}\sin {l_1}\bar y\sin {k_0}\bar x = 0, \hfill \\ - \frac{{{{({l_1}{k_0})}^2}{{\psi '}_C}^2}}{{{{(l_1^2 + k_0^2)}^2}}}{\cos ^2}{l_1}\bar y{\sin ^2}{k_0}\bar x + Ak_0^2{{\psi '}_B}\sin {k_0}\bar x\cos {l_1}\bar y + \hfill \\ \frac{{Ak_0^2l_1^2{{\psi '}_C}}}{{2(l_1^2 + k_0^2)}}\sin {l_1}\bar y\sin 2{k_0}\bar x + \frac{{k_0^2{{\psi '}_B}{{\psi '}_C}}}{{2(l_1^2 + k_0^2)}}\sin 2{l_1}\bar y\cos \cdot \hfill \\ {k_0}\bar x + \frac{{l_1^2k_0^2{{\psi '}_C}^2}}{{(l_1^2 + k_0^2)}}{\sin ^2}{l_1}\bar y{\cos ^2}{k_0}\bar x = 0. \hfill \\ \end{array} \right.$ | (32) |
公式(32)共有三个方程、四个变量(
然而,由于方程(32)是复杂的代数方程组,解出的隐式方程
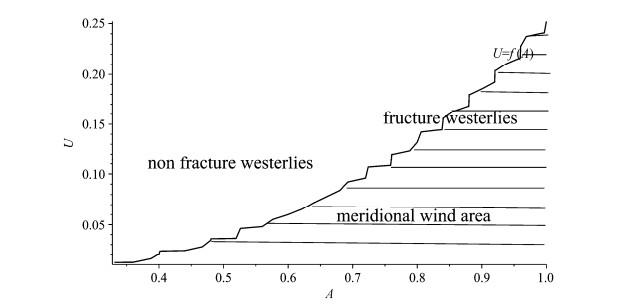
|
图 3 西风带的分类:断裂西风带[U=f(A)]、非断裂西风带[U>f(A)]和径向风带[U<f(A)] Fig. 3 Classification of in the westerlies: Fructure westerlies [U=f(A)], non fructure westerlies [U > f(A)], and meridional wind area [U < f(A)] |
根据图 3,可以看出,在整个
结构方程(14)中的扰动涡度系数
第1天,水平涡动量输送
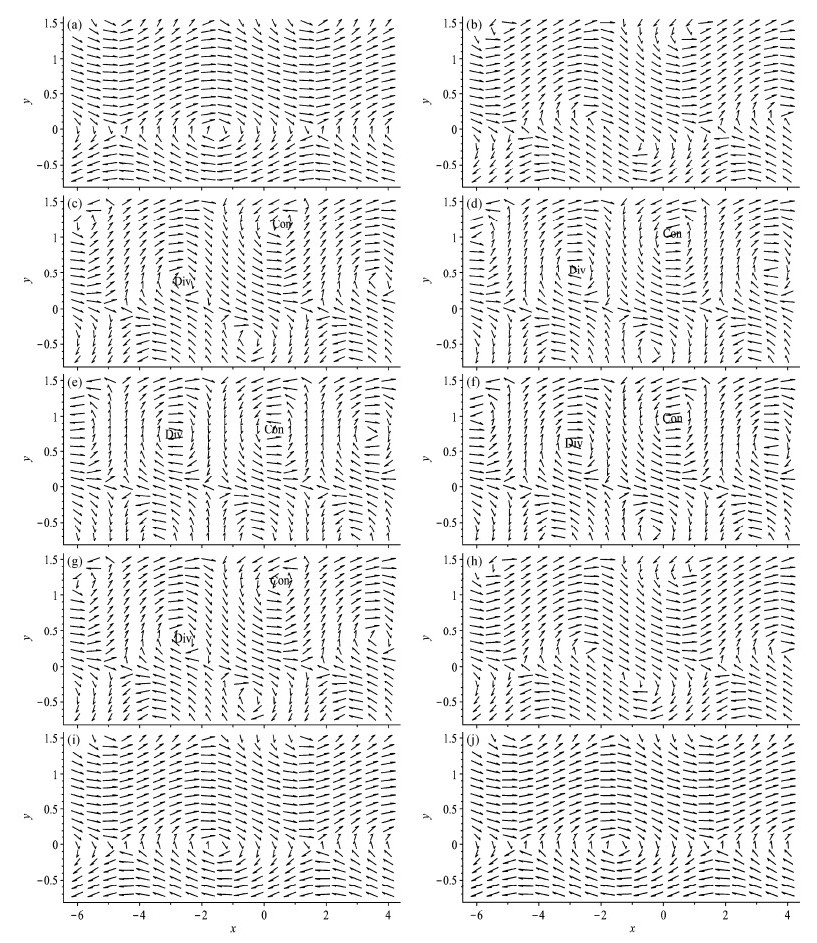
|
图 4 同图 2,但为西风环流 |
根据能量守恒原理,水平涡动量输送不可能无限增长,甚至不能长久维持,在一段时间后,水平涡动量输送
本研究运用准地转模式,通过等值投影的方法,将地转流函数的等值线转换为向量场结构,探讨西风带高低指数周期性转换的机制,结果表明:(1)仅有位能转化所引起的水平涡动输送,可以产生大振幅的行星波,但不会产生西风带的断裂;(2)波流相互作用下,平均纬向风速U与基波波幅
本文虽然较好地描述了高低指数间结构的变化及准周期循环,但仍然存在以下几个问题:(1)对流层高层的动能和热能输送对于西风带高低指数环流的形成、维持是重要的,也就是西风带具有一定的斜压性质,表明本研究的正压模式存在一定的局限性;(2)西风带高低指数环流之间的转换具有一定的跳跃性质,而本研究的转换是连续性的,没有体现突变这一特征;(3)外源强迫对于西风带高低指数环流的形成、维持的重要作用,模式中忽略了地形和热源等外源强迫的作用,只研究了大气内部动力机制,这些不完善有待今后深入的研究,从理论上进一步逼近实际大气中各个物理量相互作用后的结果。
Charney J G, DeVore J G. 1979. Multiple flow equilibria in the atmosphere and blocking[J]. J. Atmos. Sci., 36(7): 1205-1216. DOI:10.1175/1520-0469(1979)036<1205:MFEITA>2.0.CO;2
|
Charney J G, Straus D M. 1980. Form-drag instability, multiple equilibria and propagating planetary waves in baroclinic, orographically forced, planetary wave systems[J]. J. Atmos. Sci., 37(6): 1157-1176. DOI:10.1175/1520-0469(1980)037<1157:FDIMEA>2.0.CO;2
|
Deininger R C. 1982. Topographically forced wave instability at finite amplitude[J]. J. Atmos. Sci., 38(12): 2619-2625. DOI:10.1175/1520-0469(1981)038<2619:TFWIAF>2.0.CO;2
|
Ding Q H, Wallace J M, Battisti D S, et al. 2014. Tropical forcing of the recent rapid Arctic warming in northeastern Canada and Greenland[J]. Nature, 509(7499): 209-212. DOI:10.1038/nature13260
|
Ding Q H, Schweiger A, L'Heureux M, et al. 2017. Influence of high-latitude atmospheric circulation changes on summertime Arctic sea ice[J]. Nat. Climate Change, 7: 289-295. DOI:10.1038/nclimate3241
|
Francis J A, Chan W H, Leathers D J, et al. 2009. Winter Northern Hemisphere weather patterns remember summer Arctic sea-ice extent[J]. Geophys. Res. Lett., 36(7): L07503. DOI:10.1029/2009GL037274
|
Francis J A, Vavrus S J. 2012. Evidence linking Arctic amplification to extreme weather in mid-latitudes[J]. Geophys. Res. Lett., 39(6): L06801. DOI:10.1029/2012GL051000
|
高普云. 2005. 非线性动力学——分叉、混沌与孤立子[M]. 长沙: 国防科技大学出版社: 73-74. Gao Puyun. 2005. Nonlinear Dynamics-Bifurcations, Chaos, and Solitons[M] (in Chinese). Changsha: NUDT Press: 73-74.
|
Gill A E. 1974. The stability of planetary waves on an infinite beta-plane[J]. Geophys. Fluid Dyn., 6(1): 29-47. DOI:10.1080/03091927409365786
|
郭大钧. 2001. 非线性泛函分析[M]. 2版. 济南: 山东科学技术出版社: 34-36. Guo Dajun. 2001. Nonlinear Functional Analysis[M] (in Chinese). 2nd ed. Jinan: Shandong Science and Technology Press: 34-36.
|
Hoskins B J, Hollingsworth A. 1973. On the simplest example of the barotropic instability of Rossby wave motion[J]. J. Atmos. Sci., 30(1): 150-153. DOI:10.1175/1520-0469(1973)030<0150:OTSEOT>2.0.CO;2
|
金飞飞, 朱抱真. 1986a. 强迫波、自由波和纬向气流的相互作用——Ⅰ.平衡态环流的分支[J]. 中国科学B辑, (6): 663-672. |
Jin Feifei, Zhu Baozhen. 1988. Interaction of forced waves, free wave and zonal flow (Ⅰ)-Bifurcation of the equilibria[J]. Scientia Sinica (Series B), 31(4): 469-480.
|
金飞飞, 朱抱真. 1986b. 强迫波、自由波和纬向气流的相互作用——Ⅱ.高低指数的转换和振荡的定性分析[J]. 中国科学B辑, 16(8): 889-896. Jin Feifei, Zhu Baozhen. 1986b. The interaction of forced waves, free waves and zonal flow (Ⅱ)-Qualitative analysis of the conversion and oscillation about high and low index cycles[J]. Scientia Sinica (Series B) (in Chinese), 16(7): 889-896.
|
刘式达, 刘式适. 2011. 大气涡旋动力学[M]. 北京: 气象出版社: 212-213. Liu Shida, Liu Shishi. 2011. Atmospheric Vortex Dynamics[M] (in Chinese). Beijing: China Meteorological Press: 212-213.
|
刘式适, 刘式达, 谭本馗. 1996. 非线性大气动力学[M]. 北京: 国防工业出版社: 134-135. Liu Shishi, Liu Shida, Tan Benkui. 1996. Nonlinear Atmospheric Dynamics[M] (in Chinese). Beijing: National Defend Industry Press: 134-135.
|
Lorenz E N. 1972. Barotropic instability of Rossby wave motion[J]. J. Atmos. Sci., 29(2): 258-265. DOI:10.1175/1520-0469(1972)029<0258:BIORWM>2.0.CO;2
|
罗德海. 2000. 阻塞非线性动力学[M]. 北京: 气象出版社: 67. Luo Dehai. 2000. Blocking Nonlinear Dynamics[M] (in Chinese). Beijing: China Meteorological Press: 67.
|
吕美仲, 侯志明, 周毅. 2004. 动力气象学[M]. 北京: 气象出版社: 137-138. Lü Meizhong, Hou Zhiming, Zhou Yi. 2004. Dynamic Meteorology[M] (in Chinese). Beijing: China Meteorological Press: 137-138.
|
Mitchell K E, Dutton J A. 1981. Bifurcations from stationary to periodic solutions in a low-order model of forced, dissipative barotropic flow[J]. J. Atmos. Sci., 38(4): 690-716. DOI:10.1175/1520-0469(1981)038<0690:BFSTPS>2.0.CO;2
|
Namias J. 1950. The index cycle and its role in the general circulation[J]. J. Atmos. Sci., 7(2): 130-139. DOI:10.1175/1520-0469(1950)007<0130:TICAIR>2.0.CO;2
|
Overland J E, Wang M Y. 2010. Large-scale atmospheric circulation changes are associated with the recent loss of Arctic sea ice[J]. Tellus A, 62(1): 1-9. DOI:10.1111/j.1600-0870.2009.00421.x
|
Simmons A J, Wallace J M, Branstator G W. 1983. Barotropic wave propagation and instability, and atmospheric teleconnection patterns[J]. J. Atmos. Sci., 40(6): 1363-1392. DOI:10.1175/1520-0469(1983)040<1363:BWPAIA>2.0.CO;2
|
王为德. 1983. 瞬时经圈环流与西风带环流变化的关系[J]. 气象学报, 41(2): 138-146. Wang Weide. 1983. On the relation between the mid-latitude meridional cell and the change of zonal circulation[J]. Acta Meteorologica Sinica (in Chinese), 41(2): 138-146. DOI:10.11676/qxxb1983.016
|
叶笃正, 朱抱真. 1958. 大气环流的若干基本问题[M]. 北京: 科学出版社: 33-34. Ye Duzheng, Zhu Baozhen. 1958. Basic Problems of Atmospheric Circulation[M] (in Chinese). Beijing: Science Press: 33-34.
|
曾庆存. 1979. 旋转大气中运动的非线性相互作用和旋转适应过程[J]. 中国科学, 22(10): 986-995. Zeng Qingcun. 1979. On nonlinear interaction of motion and process of rotational adaption in rotating atmosphere[J]. Scientia Sinica, 22(8): 945-957.
|
张恭庆, 林源渠. 1987. 泛函分析讲义[M]. 北京: 北京大学出版社: 103-104. Zhang Gongqing, Lin Yuanqu. 1987. Functional Analysis Handout[M] (in Chinese). Beijing: Peking University Press: 103-104.
|
张锦炎. 1981. 常微分方程几何理论与分支问题[M]. 北京: 北京大学出版社: 64-65. Zhang Jinyan. 1981. Geometric Theory and Branch Problems of Ordinary Differential Equations[M] (in Chinese). Beijing: Peking University Press: 64-65.
|
朱抱真, 金飞飞, 刘征宇. 1991. 大气和海洋的非线性动力学概论[M]. 北京: 海洋出版社: 89-89. Zhu Baozhen, Jin Feifei, Liu Zhengyu. 1991. An Introduction to the Nonlinear Dynamics of the Atmosphere and Ocean[M] (in Chinese). Beijing: China Ocean Press: 89-89.
|
 2019, Vol. 43
2019, Vol. 43


