大气圈是一个复杂多变的多尺度非线性系统(Ji and Wang， 1995；Wang and Ji， 1995)，它的发展和演变受诸多因素(如动力、热力和化学等)的影响。综合考虑这些影响因素，我们可以把大气体系描述成一组非常复杂的非线性非齐次偏微分方程组。到目前为止，还没有人能从数学上求出这组方程的精确解。因此，用数值分析的方法来求解大气方程组从而研究大气运动规律成为目前大气科学领域的主要的研究手段之一(季仲贞，1986；季仲贞和王斌，1991；林万涛等，2008)。

数值模拟大气方程最终往往会归结为求解一个大规模离散系统，其中计算稳定性与计算速度是两个主要研究内容。对大规模离散系统的求解，是许多科学与工程计算中数值模拟的中心问题，而且通常在计算中是最耗时间的部分。在数值模拟过程中，为了保障模式的计算稳定性和准确性(Lilly，1965；Gravel et al., 1993；Ramage，1999)，所能选取的时间步长是较小的。针对不同的问题和不同的分辨率，其时间步长可能是几分钟，也可能是半小时，至多取一小时，其计算步数一般是较多的。此外，为了保证计算的精度，模式的空间分辨率又不能太低，所以其总的计算量是巨大的。面对如此巨大的计算量，在目前计算机资源远不能满足实际需要的情况下，人们只能借助于数值算法来达到减少计算机存储和加快计算速度的目标，而预处理迭代算法则是目前实现这个目标的重要手段。

预处理方法的优点体现在迭代次数与计算时间总量的减少。目前，预处理主要归结为代数预处理(Saad and Schultz， 1986; Chow，2000; Chen，2001; Benzi，2002; 王光辉等，2008)和基于PDES(Partial Differential EquationS)的预处理(Mousseau et al., 2000，2002；Reisner et al., 2001，2003)。前者对应的离散系统为线性系统。后者则对应非线性离散系统。代数预处理方法有简单、适应性广等特点，但离散系统的线性化要求会使非线性方程的求解失去无可挽回的精度。基于PDES的预处理方法能处理非线性离散系统，非线性离散系统往往更能反应原始方程，但其求解往往会很复杂。首先必须用迭代法处理其非线性，然后在每一时间步长内求解一个规模很大的线性方程组。应用预处理JFNK(Jacobian-Free Newton-Krylov)方法能有效地求解隐式非线性离散系统。这是一种对非线性系统进行双重循环求解的方法。外循环用Newton迭代方法将非线性离散系统在每一时间步内化为线性问题，而且无须计算和存储Jacobian迭代矩阵。内循环用Krylov迭代法求解每一时间步内的线性系统。两重循环联合起来就称为JFNK方法。该方法的成功应用主要取决于对每一时间步内线性系统的预处理。预处理的方法有很多，其最有效的是用原始方程的显式或半隐式等求解器作为预处理方法。有关这方面的研究取得了非常丰富的成果，如：Brown and Saad(1990)对相关Krylov子空间方法的基本原理和应用作了较为细致的研究；Mousseau et al.(2002)为有效地求解隐式非线性差分方程，并从理论上分析了预处理JFNK 方法的计算精度与计算可行性；Knoll and Keyes(2004)对预处理JFNK方法的应用和发展作了全面的总结；Mousseau et al.(2000)用算子分裂法作为预处理方法对非平衡辐射扩散问题进行求解；Mousseau et al.(2002)以二维浅水方程为应用背景，提出了隐式非线性相容求解技巧，该技巧的特点是用时间分裂求解法作为预处理方法，通过对系统中最大时间尺度的有效消除，Krylov迭代次数明显减少，使JFNK方法的整体有效性增加；Reisner et al.(2003)在求小尺度热驱动大气流的全隐式解时用半隐式离散预处理方法来减少Krylov迭代次数，并将该预处理方法用到了隐式平衡飓风模型JFNK方法的求解中，提出了所谓的隐式平衡方法(Reisner et al., 2005)。为了量化新方法对比传统方法的有效性和准确性，本文首次用降水湿泡模拟实验对隐式平衡求解器与半隐式方法进行了比较。降水湿泡试验显示：对于给定的精度，隐式平衡方法无论比一阶半隐式方法还是传统的蛙跳半隐式方法都更有效。此外，线性多重网格方法、非线性多重网格方法及快速Fourier变换法等也被作为预处理方法应用于JFNK方法。

本文第二部分介绍预处理JFNK快速算法及基本步骤。第三部分以一维浅水波方程为例，描述预处理矩阵的构造及预处理方法在JFNK算法中的应用。构造浅水波模型的隐式非线性差分格式及其半隐式差分格式。比较了应用预处理JFNK方法求解隐式非线型差分格式及直接求解半隐式差分格式的结果。文章的最后我们对预处理JFNK方法作了简单的总结并对有关问题作了初步探讨。

2 预处理JFNK方法2.1 预处理方法

JFNK方法是一种嵌套式迭代算法。一般有Newton修正迭代外循环与建立Krylov 子空间的内循环。在Krylov内循环内，通常需要一个预处理器，用以提高JFNK方法的有效性。预处理JFNK方法的目的是用来减少GMRES(Genera-lized Minimal RESidual)的迭代次数。GMRES是一种基于Arnoldi(或Householder)方法的非对称求解器(Saad and Schultz， 1986)，构造近似解的基础是Krylov子空间，而利用Arnoldi(或Householder)方法求Krylov子空间的标准正交基是实现这一算法的关键。它的收敛其决于矩阵的特征值而不是矩阵的结构。对线性系统采用左乘或右乘一个预先选定的矩阵，使其接近于单位矩阵，然后再进行迭代求解，这样能十分显著地减少求解的迭代次数，从而达到减少计算量的目的。预处理器的选取方法有许多，普通的方法是选择一个只需迭代几步的简单迭代方法作为预处理器。而一个有效的JFNK方法不但要回避Jacobian 矩阵的形成，而且其预处理器将比系统的Jacobian 矩阵更为简单。最近发展起来用来预处理JFNK的预处理器是一种叫做基于物理意义(或微分方程)的预处理方法。这种方法非常有效，其本质是基于描述物理问题的微分方程问题，用一种简易离散格式的求解法去预处理较为复杂的离散格式。例如：对于浅水波方程，我们可以用半隐式格式、半隐式-半拉格朗日格式等的求解器或用离散格式的不完全LU分解法、时间分裂法等作为预处理器去求解非线性隐式方程。

总之，对于非线性隐式格式的求解，需把预处理、Jacobian-Free和GMRES迭代法等几种有效工具结合起来才能达到在保证计算精度的前提下提高其计算效率。

2.2 算法的基本步骤2.2.1 Newton 迭代(Dembo et al., 1982)

设隐式非线性差分方程为：

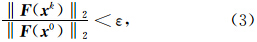
2.2.2 预处理

对线性方程(1)进行预处理以减少迭代求解时的迭代次数。设预处理阵为P，那么经过预处理后方程(1)变为(Mousseau et al., 2002)：

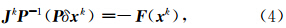
用重启动GMRES(m)(m表示重启动的次数)迭代算法求解方程(5)(Saad and Schultz， 1986)。

(1)输入F(x^k)及初始向量v₀，最大迭代次数m及精度要求ε。这里v₀=P^-1F(x^k)，在迭代过程中只用到J′与v的积，所以无需计算J′。

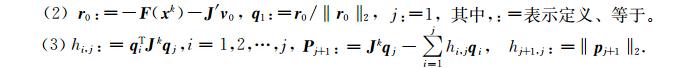
(4)如果h_j+1，j＜ε 或 j=m，则转下一步; 否则

(5)求解最小二乘问题

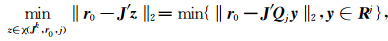
(6)如果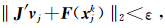，则输出v_j，结束; 否则v₀:=v_j，转第(2)步。

在上述GMRES(m)迭代求解方程(5)的过程中，正交向量组q₁，q₂，…，q_i的计算与存储不能回避，但可用重启动方法减少存储量。 而对Jacobian的计算与存储可以回避。很明显，在上面的GMRES(m)迭代中，我们只用到Jaco-bian矩阵与一个向量的乘积J′v，对于小规模问题，我们可以通过已知函数向量F。但由于F是一个满矩阵，对于大规模问题，若先求出J′，然后再计算J′v，则需占用巨大的空间存储J′。为此我们用差商来逼近乘积J′v，即：

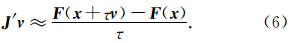
为了验证我们的预处理迭代方法的效果，这里我们以浅水模型的隐式非线性格式为例，用半隐式格式求解方法做预处理器进行预处理JFNK 求解。并与半隐式格式的求解比较其计算有效性。我们选择无地形通量形式的一维浅水波方程进行数值实验。我们增加了一项附加力以保证解析解的封闭性。微分方程为(Reisner et al., 2001):

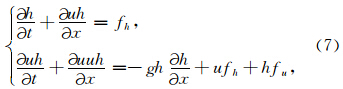
由文献Reisner et al.(2001)，方程组(1)有下列解析解：

下面对方程组(7)进行差分离散，获得全隐式非线性离散和半隐式线性格式(见3.2节和3.3节)。i取1，2，3…，N，0、N+1为边界点。

3.2 全隐式非线性格式

3.3 半隐式格式

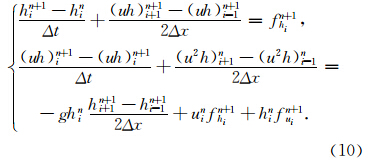
将半隐式方程写成Pδw=-F(w)形式。设δh=hⁿ⁺¹-hⁿ，δ(uh)=(uh)ⁿ⁺¹-(uh)ⁿ. 则上述半隐式方程写为:

差分方程组中的参数取值如下：g=1.0 m·s^-2，h₀=1.0 m，a_h=0.01 m，a_u=0.01 m·s^-1，k=2 m^-1，ω=0.0 s^-1，x∈[0，2π]，t∈[0，2π].

计算中取如下截断误差

3.5 预处理结果比较

这部分我们将简要地说预处理前后求解(9)的结果进行比较。先将半隐式差分格式(10)写成

首先我们通过方程组(12)求解方程组(10)，GMRES(m)迭代收敛误差取为ε＜10^-6，重启动参数m=10。然后用半隐式格式(10)的求解器做预处理器去求解全隐式非线性格式(9)，外循环Newton迭代收敛误差与内循环GMRES(m)迭代收敛误差均取为ε＜10^-6。

为测试预处理前后GMRES迭代次数、运算时间与时空分辨率及与收敛精度的关系，我们通过：固定时间步数，空间分辨率逐步提高；固定空间步数，时间分辨率逐步提高及时空步长按一定比率同步提高等3个试验比较预处理效果。

表 1为当时间步数固定为N=320时，随着空间分辨率的提高(m增大)，预处理前后，求解平均每时间步长GMRES迭代次数和总的CPU时间的比较。从表中的数字看出，随着空间分辨率的提高，预处理前后每时间步的平均迭代次数逐步增加，但预处理后的迭代次数及总的CPU时间减少幅度较大。而且，从变趋势看，随着计算规模增大，预处理后的平均迭代次数及总的计算时间减少的比率越大。如：当m=50，预处理后的平均迭代次数虽然只有预处理前的40%，但总的计算时间却相当。这是因为预处理所花的时间基本抵消了线性系统迭代次数减少所节省的时间。而当空间步数800时，其迭代次数为预处理前求解迭代次数的23%。所用总的CPU时间仅为预处理前的一半多一点。还有，由于我们在每次牛顿迭代和GMRES迭代所用的初值都是前一时间的数值解，所以，不用预处理求解线性系统所需的迭代次数就很少，尽管如此，预处理效果仍然很明显。

表 1(Table 1)

表 1 时间步数固定为N=320，预处理前后平均每时间步长Krylov迭代次数和总的CPU时间的比较Table 1 Comparison of averaged Krylov iterative number per time step and the total CPU time with and without precondition when the total number of the time steps is fixed as N=320 预处理前 预处理后 M 平均迭代次数 总CPU时间/s 平均迭代次数 总CPU时间/s 50 5 0.891000 2 0.875000 100 5 1.188000 2 1.172000 200 5 2.859000 2 2.406000 400 6 4.375000 2 3.000000 800 13 13.93800 3 7.578000

表 1 时间步数固定为N=320，预处理前后平均每时间步长Krylov迭代次数和总的CPU时间的比较 Table 1 Comparison of averaged Krylov iterative number per time step and the total CPU time with and without precondition when the total number of the time steps is fixed as N=320

表 2为当空间步数固定为m=400时，随着时间分辨率的提高(N增大)，预处理前后平均每时间步长GMRES迭代次数和总的CPU时间的比较。随着时间步长减小，预处理前后的平均迭代次数均呈现减少的趋势，这是因为时空步长的比在逐渐减小，迭代矩阵的条件数变好，故而有迭代次数由减少的变化。虽然如此，预处理后的效果仍然很明显。

表 2(Table 2)

表 2 空间步数固定为M=400，预处理前后平均每时间步Krylov迭代次数和总的CPU时间的比较Table 2 Comparison of averaged Krylov iterative number per spacial step and the total CPU time with and without precondition when the total number of the time steps is fixed as M=400 预处理前 预处理后 N 平均迭代次数 总CPU时间/s 平均迭代次数 总CPU时间/s 100 36 4.453000 3 1.125000 160 15 3.531000 2 1.625000 220 9 3.594000 2 2.266000 280 7 3.985000 2 2.891000 300 7 4.219000 2 3.234000

表 2 空间步数固定为M=400，预处理前后平均每时间步Krylov迭代次数和总的CPU时间的比较 Table 2 Comparison of averaged Krylov iterative number per spacial step and the total CPU time with and without precondition when the total number of the time steps is fixed as M=400

为了测试我们所采用的预处理迭代法是优化稳定的，我们用时空同步加密的办法计算了预处理前后总的GMRES迭代次数和求解所需总的CPU时间。 从表 3看出，平均每时间步的迭代次数随系数矩阵的规模增大而减少，预处理效果仍非常明显。

表 3(Table 3)

表 3 当时间步长和空间步长以一定的比率减少(即τ保持不变)时，预处理前后平均每时间步Krylov迭代次数和总的CPU时间的比较Table 3 Comparison of averaged Krylov iterative number per time step and the total CPU time with and without precondition when both the time step length and the spacial step length are reduced according as a certain ratio(i.e.τ keeps a constant) 时空步长按比率变化(M×N) 预处理前 预处理后 平均迭代次数 总CPU时间/s 平均迭代次数 总CPU时间/s 50×20 30 0.094000 3 0.047000 100×40 25 0.313000 3 0.125000 200×80 19 1.188000 3 0.563000 400×160 15 3.547000 3 1.641000 800×320 13 13.969000 3 7.609000

表 3 当时间步长和空间步长以一定的比率减少(即τ保持不变)时，预处理前后平均每时间步Krylov迭代次数和总的CPU时间的比较 Table 3 Comparison of averaged Krylov iterative number per time step and the total CPU time with and without precondition when both the time step length and the spacial step length are reduced according as a certain ratio(i.e.τ keeps a constant)

图 1 表示时空网格剖分因子(即：时空网格被等分成2^κ份，κ即为剖分因子)与近似解截断误差间的关系。反映了方程组(9)的数值解随着时空网格的加密将趋于方程组(7)的解。

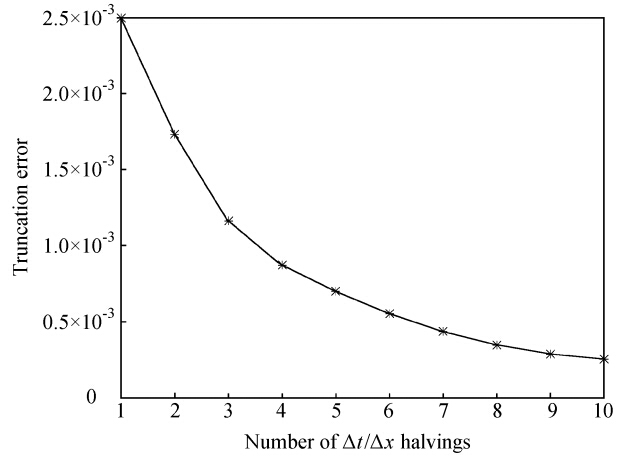图 1 剖分因子与截断误差的关系Fig. 1 The relation between the partition factor and the truncation error

图 2 表示迭代收敛误差的对数与平均每时间步长迭代次数的关系。图形反应了预处理JFNK 方法更快的收敛性。图 2中带有星号的连线是预处理前的结果，从图形的走向我们可看出：随着迭代收敛误差的减少，平均每时间步长的Krylov 迭代次数迅速增加。而经过预处理后(见图 2中带空心圆的连线)，平均每时间步长的Krylov迭代次数的增加则相对缓慢。

图 2 M=400，N=160时，迭代收敛误差的对数与平均每时间步迭代次数的关系Fig. 2 The relation between the logarithm of the iterative convergence error and the averaged iterative number per time step when M=400，N=160

本文以一维浅水方程为例对隐式非线性差分格式的求解作了一些初步尝试，对预处理JFNK快速算法从理论结果、具体构造及数值验证做了较为全面的分析。预处理JFNK快速算法虽然在实际应用中需用到双重迭代，但如果预处理方法及相关参数选取合适，将会带来非常高的计算效率。特别是超大规模的计算，这种效果会更明显。本文仅选取为半隐式差分格式的求解器做预处理方法，进行了数值试验。实际上类似的预处理方法有很多。从理论上讲，用连续方程构造的差分格式的求解器做预处理器比代数预处理方法构造的预处理器更为有效。所以是一种值得在数值天气预报中推广应用的快速算法。