2. 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室,北京 100029;
3. 中国科学院研究生院,北京 100049
2. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. Graduate University of Chinese Academy of Sciences, Beijing 100049
混沌动力系统的研究起源于Poincare(1890),而后被许多研究者逐步发展和完善。在微分方程定性理论中,Lyapunov 指数是一种常用的分析动力系统性质的方法(Oseledec,1968)。Lyapunov 指数可以刻画动力系统初始误差的整体(长期)平均增长速率,为分析动力系统的特性提供了重要信息。当动力系统至少存在一个正的Lyapunov 指数时,表示系统初始临近轨道随时间是发散的,系统是混沌的。如果初始误差为δ0 而允许的最大误差记为Δ,最大Lyapunov 指数λmax 可以用来定义混沌系统的可预报期限:
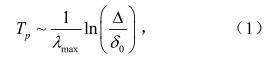
使用微分方程的定性理论在研究非线性动力系统轨道的空间结构、混沌吸引子等方面取得了巨大的成功,而使用非线性局部Lyapunov 指数在研究误差的发展规律、可预报性方面有着重要的应用价值。以往的误差理论在误差发展规律的研究方面多集中于切线性模式,为了避免线性近似的缺陷,借鉴误差的非线性发展理论的做法,我们对非线性的误差发展方程进行研究。本文将原始非线性方程和它对应的误差方程系统合在一起看作一个广义的微分动力系统,应用定性理论分析此误差系统长期的动力学行为和性质,进而研究误差发展空间中的吸引子的结构,这对认识误差发展的规律是有重要意义的。
2 Lorenz方程的误差方程及其稳定点Lorenz(1963)通过定性分析和数值试验指出一个确定的非线性动力系统可以有非常复杂的解,他所使用的 Lorenz63 方程被广泛用于混沌和可预报性方面的研究。Lorenz63 方程可以写为
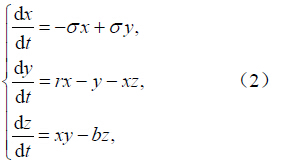
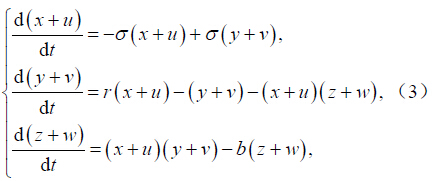
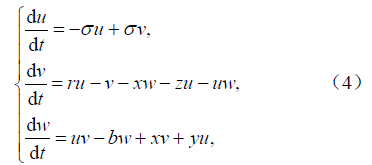
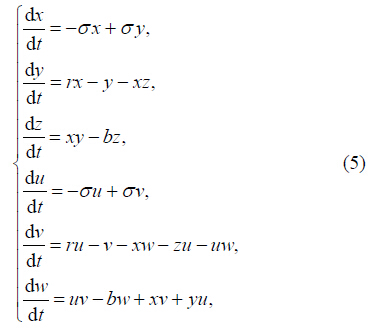
对于方程(5)可研究其稳定点问题,即求解
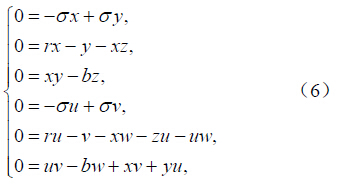
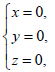 有3 组解:
有3 组解: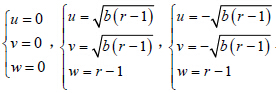 对于
对于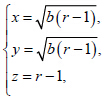 有3 组解:
有3 组解: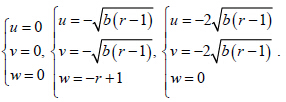 对于
对于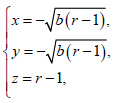 有另外3 组解:
有另外3 组解: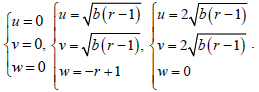
不考虑 (x,y,z) 的变化,只考虑 (u,v,w) 的吸引中心,可以发现误差的吸引子的中心有7 个(9个解中去掉2 个重合的误差中心点),分别为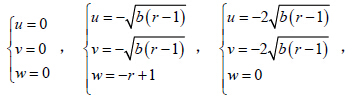
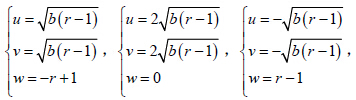
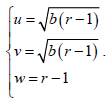 若只研究(u,v)的二维图形,不考虑w 的变化则为5 个中心区,这与解的吸引子中心在位置和数量上是不同的(解的定点个数为3)。
若只研究(u,v)的二维图形,不考虑w 的变化则为5 个中心区,这与解的吸引子中心在位置和数量上是不同的(解的定点个数为3)。
图 1a 为通过数值试验得到的误差(u,v,w)在(u,v)平面上的投影,可见较为明显的有 5 个中心区(由于不考虑w 的作用,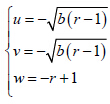 与
与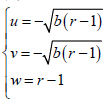 重合;
重合;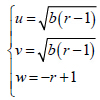 与
与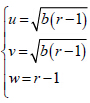 重合;与图 1b中解(x,y,z)在(x,y)平面上投影明显不同,图 1b 中的中心区域可以明显地看出来为3 个(0 点及两个吸引子中心)。误差的图像中除了中心区的位置和数量不同,轨迹的分布形式也更为复杂。
重合;与图 1b中解(x,y,z)在(x,y)平面上投影明显不同,图 1b 中的中心区域可以明显地看出来为3 个(0 点及两个吸引子中心)。误差的图像中除了中心区的位置和数量不同,轨迹的分布形式也更为复杂。
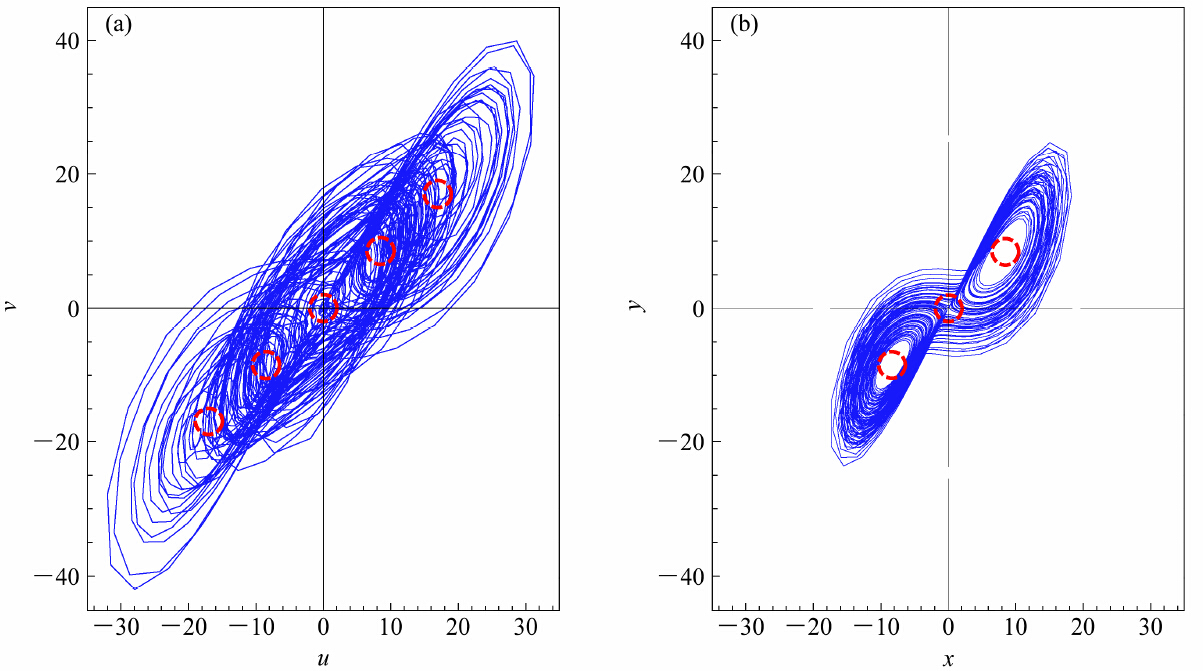 | 图 1 方程(5)计算所得的t ∈[0,100]时刻的数值解,初值为(x0,y0,z0)=(5,10,5)、(u0,v0,w0)=(0.01,0.01,0.01)(红色虚线所示区域为稳定点的位置):(a)误差(u,v,w)在(u,v)平面上的投影;(b)变量(x,y,z)在(x,y,)平面上的投影Fig. 1 The solution of Equation 5 for time t ∈[0,100] with the initial condition(x0,y0,z0)=(5,10,5) and (u0,v0,w0)=(0.01,0.01,0.01)(the red dashedline indicates the location of the stable points):(a)The projection of error (u,v,w) in (u,v) plane;(b)the projection of the variable (x,y,z) in (x,y,) plane |
方程(5)一共有9 个平衡点,知道了这些平衡点后,可以用经典的微分方程理论分析方程(5)在平衡点附近的变化趋势。对方程(5)在定点附近做小参数展开,略去高阶项得
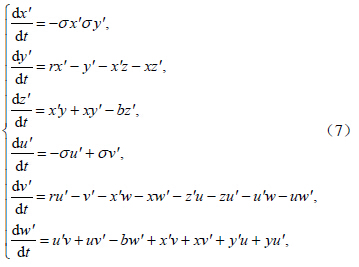
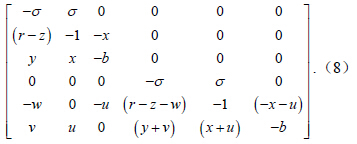
对于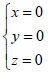 且
且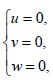 线性化矩阵(8)变为
线性化矩阵(8)变为
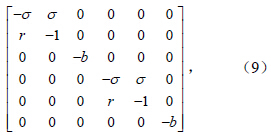
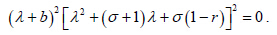
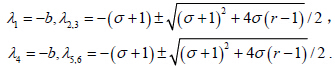
对于第二组解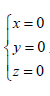 且
且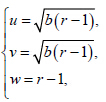 方程(8)变为
方程(8)变为
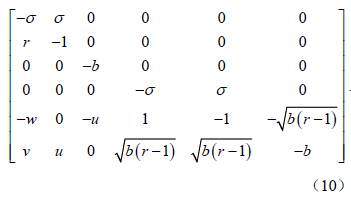
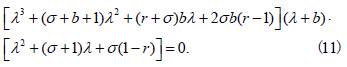
对于第三组解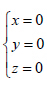 且
且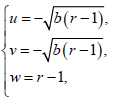 方程(8)变为
方程(8)变为
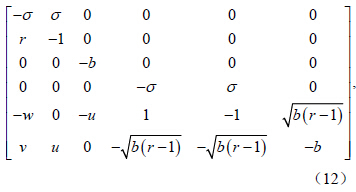
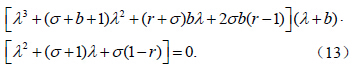
对其它的6 组解,重复这个过程可以发现:虽然线性化矩阵的阶数为6,但方程(8)特征根的值与Lorenz 方程的特征根值是一样的(详细证明见第5 节)。在进行稳定性分析时,关注的是复数根中实部的正负号问题,以确定系统是渐近稳定还是发散,因此关于Lorenz 方程中r 的取值范围经典分析也适用于这个误差方程。即当1< r < 24.74时,有稳定的平衡态,r > 24.74时为混沌状态。
4 误差方程的吸引性质证明一个光滑的微分动力系统存在吸引子和存在混沌吸引子是两个不同的问题。一般来说,证明存在吸引子只需要证明其轨道收敛到一个不变的点集即可。而混沌吸引子除了这个要求以外还需要证明其对初值的敏感性,因此是更为困难的。混沌吸引子的存在性证明一般使用的是Silnikov方法或判据(Silva,1993),而吸引子的存在性证明可以采用丑纪范(1983)、李建平和丑纪范(1997)的方法。
对方程组(5)做如下变换:
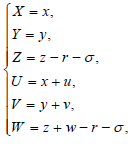
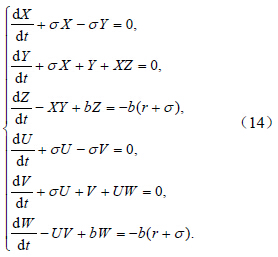

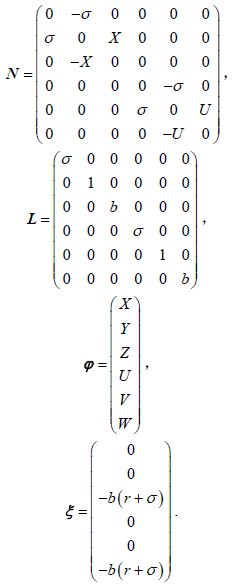
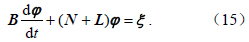
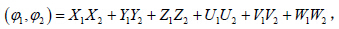
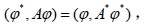
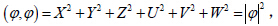
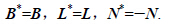
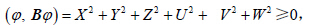
以 ϕ 对方程(15)做内积有:则方程(14)可以改写为算子方程:

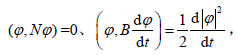
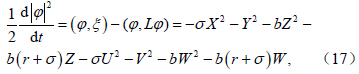
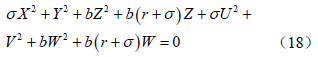
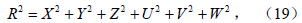
Kalnay(2002)研究Lorenz63 模型时以流的散度
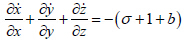
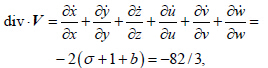
证明:记 E = uiu + vjv + wkw表示误差向量,定义模

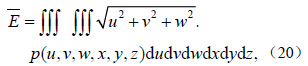
定义一个常微分系统:
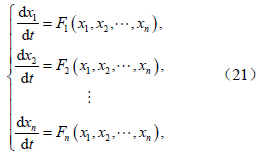
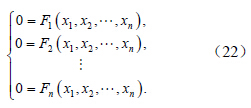
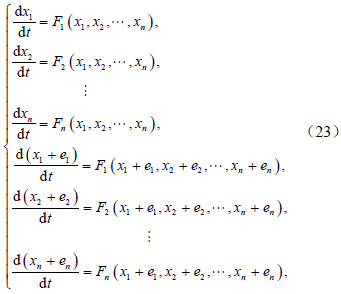

对方程组(24)中的后n 个方程,做变量替换yi=xi+ei,转化为:
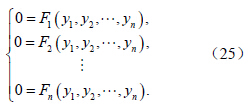
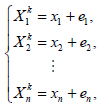
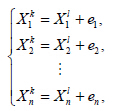
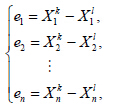
知道了误差的稳定点之后,根据动力系统稳定性的理论,只要研究方程组(23)的线性化系统的特征值问题,就能知道误差系统在稳定点附近的性质。
对应方程组(21)的线性化系数矩阵为:


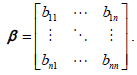
矩阵(26)对应的特征值方程为 λ I − A = 0,每个定点对应一组特征值 λ =(λ1,λ2,…,λn),共有 m组。误差方程(27)的特征值方程可化为:(λ I − A)(λ I − β ) = 0,而(λ I − β )= 0得到的 m 组特征值为 λ I − A = 0得到的 m 组特征值的另一个排列,因此并没有产生新的特征值,而且最大的特征值 λmax 也相同,因此对于矩阵(26)中各参数的取值而引起的平衡点特性的结果,也适用于误差方程。
6 小结将Lorenz 方程及其导出的误差方程作为联立方程来研究误差的性质,对联立方程的稳定性分析表明,Lorenz 系统的全误差方程共有9 个平衡点,如果只考虑误差定点的位置(不考虑解的定点位置),那么误差的平衡点为7 个。误差方程可以改写为一个特殊的算子方程,误差轨线将收敛于一个有限的区域,此外误差方程对应的流的散度为负值,因此其在相空间中的体积不断收缩,最终趋向一个低纬曲面,在相空间中趋向于体积为0 的不变点集,因此误差方程具有吸引子。当t→∞时,误差 (u,v,w) 的轨迹在吸引域中的概率分布是确定的,因此平均饱和误差 E 是确定的常数。这个结果可以解释小初始误差经过一段时间的发展之后,趋向饱和的现象。
除了讨论Lorenz 方程,本文还把针对Lorenz方程的误差联立方程方法拓展到一般的常微分动力系统,展示了对一般误差方程的特征矩阵进行分析研究其特征行列式性质的方法,得到了一般误差系统中相应的稳定点和平衡态性质与原动力系统的稳定点和平衡态性质的关系。结果表明,误差方程对应的特征方程并没有引入与原方程不同的特征值,而只排列顺序上有所不同,因此原方程的稳定性分析和判据也适用于误差方程。
将全误差方程看作一个广义的微分动力系统来进行研究的好处是明显的,这使得我们可以将全部的研究动力系统的理论、方法和工具直接用于误差的研究和分析。应用定性理论分析全误差系统长期的动力学行为和性质,进而研究误差发展空间中的吸引子的结构,这对认识误差发展的规律是有重要意义的。本文的研究中得到了Lorenz 系统误差发展的平衡点、稳定性判据、吸引性质等以前未被误差增长理论所描述的性质,其结果除了可以解释平均饱和误差趋于常数的现象外,还可以进一步用来讨论预报期限等可预报性问题。本文只证明了误差方程具有全局的吸引子,更进一步可以使用Silnikov 方法来研究这个吸引子是否为混沌吸引子,这些问题将在下一步的工作中予以研究。
致谢感谢两名审稿人提出的细致而且有价值的建议,对提高本文质量有很大帮助。
| [1] | 丑纪范. 1983. 初始场作用的衰减与算子的特征 [J]. 气象学报, 41 (4): 385-392. Chou Jifan. 1983. Some properties of operators and the effect of initial condition [J]. Acta Meteorologica Sinica (in Chinese), 41 (4): 385-392. |
| [2] | 丁瑞强. 2007. 非线性误差增长理论与可预报性研究 [D]. 中国科学院大气物理研究所博士学位论文, 192pp. Ding Ruiqiang. 2007. Nonlinear error dynamics and predictability study [D]. Ph.D. dissertation (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Sciences, 192pp. |
| [3] | Ding R Q, Li J P. 2007. Nonlinear finite-time Lyapunov exponent and predictability [J]. Physics Letters A, 364 (5): 396-400. |
| [4] | Eckmann J P, Ruelle D. 1985. Ergodic theory of chaos and strange attractors [J]. Reviews of Modern Physics, 57 (3): 617-656. |
| [5] | Kalnay E. 2002. Atmospheric Modeling, Data Assimilation, and Predictability [M]. Cambridge: Cambridge University Press, 364pp. |
| [6] | Kazantsev E. 1999. Local Lyapunov exponents of the quasi-geostrophic ocean dynamics [J]. Applied Mathematics and Computation, 104 (2-3): 217-257. |
| [7] | 李建平, 丑纪范. 1997. 大气吸引子的存在性 [J]. 中国科学 (D辑), 27 (1): 87-96. Li Jianping, Chou Jifan. 1997. Existence of atmosphere attractor [J]. Science in China (Ser. D) (in Chinese), 40 (2): 215-224. |
| [8] | 李建平, 丁瑞强, 陈宝花. 2006. 大气可预报性研究的回顾与展望,21世纪初大气科学前沿与展望 [M]. 北京: 气象出版社, 96-104. Li Jianping, Ding Ruiqiang, Chen Baohua. 2006. Review and Prospect on the Study of Atmospheric Predictability, Frontier and Prospect of Atmospheric Sciences at the Beginning of the 21th Century (in Chinese) [M]. Beijing: China Meteorological Press, 96-104. |
| [9] | Lorenz E N. 1963. Deterministic nonperiodic flow [J]. J. Atmos. Sci., 20 (2): 130-141. |
| [10] | Lorenz E N. 1996. Predictability: A Problem Partly Solved [M]. Proc. ECMWF Seminar on Predictability, Vol. I, Reading, United Kingdom, ECMWF, 1-18. |
| [11] | Oseledec V I. 1968. A multiplicative ergodic theorem: Lyapunov characteristic numbers for dynamical systems [J]. Transactions of the Moscow Mathematical Society, 19: 197-231. |
| [12] | Poincare H. 1890. Sur le Probleme des Trois Corps et les Equations de la Dynamique [J]. Acta Mathematica, 13 (1):A3-A270. |
| [13] | Silva C P. 1993. Shilnikov’s theorem—A tutorial [J]. IEEE Transactions on Circuits and Systems, 40 (10): 675-682. |
| [14] | Wolf A, Swift J B, Swinney H L, et al. 1985. Determining Lyapunov exponents from a time series [J]. Physica D, 16 (3): 285-317. |
| [15] | Yoden S, Nomura M. 1993. Finite-time Lyapunov stability analysis and its application to atmospheric predictability [J]. J. Atmos. Sci., 50 (11): 1531-1543. |
| [16] | Ziehmann C, Smith L A, Kurths J. 2000. Localized Lyapunov exponents and the prediction of predictability [J]. Physics Letters A, 271 (4): 237- 251. |
 2012, Vol.17
2012, Vol.17 

