2. 中国人民解放军94923部队气象台, 武夷山 354301
2. No. 94923 Army of PLA Meteorological Observatory, Wuyishan 354301
干旱作为最严重的自然灾害之一,一直是科学界研究的热点。为了充分反映干旱的强度和危害程度,科学家们提出了多种干旱指数来描述干旱的特征,如降水距平百分率、Palmer指数(Palmer,1965)、标准化降水指数SPI(McKee et al., 1993; 1995)、地表湿润指数H(马柱国等,2005)、Z指数(周后福等,2010)和其他综合指数(邹旭恺等,2010)等,其中应用较为广泛的有Palmer指数、SPI和H指数等。一般认为,干旱的形成和发展是地表水分亏缺缓慢积累的过程,干旱程度应是水分亏缺量及其持续时间的函数。在全球变暖的气候背景下,气温的持续上升使得地表蒸发量迅速增加,导致地表水分收支平衡发生了新的变化。以往简单地以降水量变化作为描述干旱程度的单因素指数,如降水距平百分率、SPI和Z指数等,已不能全面地反映这种新变化。因此,干旱研究不仅要考虑地表水分的收入,还要考虑水分的支出。尽管多因素干旱指数如Palmer指数等可以较为全面反映地表水分的收支变化,但由于Palmer指数在区域可比性方面存在不足(Guttman,1998),且计算Palmer指数所需的土壤湿度资料缺乏长时间大范围尺度的观测数据,所以还不适于大范围推广。马柱国等(2005)以年降水量与年潜在蒸发总量之差定义的地表湿润指数H很好地解决了这一问题,它计算简单,又能较为全面地反映地表水分平衡过程中降水和蒸发的变化,适于推广应用。
然而干旱程度还是持续时间的函数。多数干旱指数都只具有一个时间尺度,所以只对持续时间在某一时段内的干旱响应较好,如Palmer指数对9~12个月尺度的干旱响应最好(Guttman,1998),而干旱的持续时间是随机的,因此只具有单一时间尺度的干旱指数在对干旱持续时间的表征方面显然还不够完备。McKee et al.(1993)提出的干旱指数SPI在解决这一问题上是一个突破,SPI具备进行多个时间尺度分析的能力,可以满足多种水分监测需求,如1个月尺度的SPI与土壤水分密切相关;3个月尺度的SPI可用于季节降水估计;6~9个月尺度的SPI可反映出中期降水的变化趋势;12个月尺度的SPI则反映了长期降水变化,通常与河流水位、水库水位,甚至地下水位相关度较高(Ji and Peters, 2003)。Hayes et al.(1999)认为具有多尺度分析能力的SPI还可用于持续干旱的识别和监测。所以理想的干旱指数应该具备这样的能力——不仅能识别干旱是否发生或结束,充分反映实际干旱程度,而且可以表征不同持续时间对干旱程度的影响。
Vicente-Serrano et al.(2010)在SPI的基础上提出的标准化降水蒸发指数(SPEI)正是这样一 种指数。SPEI在计算中以月水分亏缺量(water surplus or deficit,Vicente-Serrano et al., 2010)——月降水量与月潜在蒸发量之差代替了SPI计算中的月降水量,从而可以更为客观地描述当前的地表干湿变化。由于不同时间、不同地区的水分亏缺量变化幅度很大,在不同时空尺度上难于相互比较,且其概率分布是一种偏态分布,因而采用log-logistic概率分布函数来描述水分亏缺量的变化,最后经正态标准化得到SPEI值。SPEI值实质上反映的是水分亏缺量变化的分布频率。SPEI干湿等级分类见表 1。Vicente-Serrano et al.(2010)通过对热带气候区、季风气候区、地中海气候区、半干旱气候区、大陆气候区、寒带气候区和海洋气候区的研究指出,SPEI序列的变化与sc-PDSI(自适应Palmer指数)序列在各种时间尺度和不同地区均有较好的一致性,而与SPI序列只在增温不显著的地区较为相似。SPEI与sc-PDSI均能较好地表征全球变暖以来的地表干湿变化,但SPEI在计算上则更为简单。综上所述,该指数的优点可归结为:1)考虑了地表蒸发变化的影响,对全球气温快速上升导致的干旱化加剧反映敏感;2)可进行多个时间尺度分析,适用于农业干旱和水文干旱等不同类型的干旱 分析;3)计算简单,仅需要月降水和月平均气温资料,适于大范围推广应用;4)作为标准化指数,便于不同时间、不同地区之间进行对比分析;5)可用于干旱识别和监测。
|
|
表 1 SPEI干湿等级分类 Table l Classification scale for st and ardized precipitation evapotranspiration index(SPEI) |
既然SPEI是在SPI的基础上发展而来的,那么在继承SPI优点的同时,是否完全克服了SPI的不足呢?类似SPI基于Gamma分布,SPEI是基 于log-logistic分布的分布频率值。而通过分布函数计算得到的分布频率值在某些特殊条件下会出现异常,如Wu et al.(2007)研究指出,在干旱区的枯水期,由于无降水月份(月降水量为0)过多,会导致小尺度的SPI指数偏大而无法表征实际干旱程度。尽管Vicente-Serrano et al.(2010)认为三参数log-logistic概率分布函数的使用显著改善了这一问题,但由于Vicente-Serrano et al.(2010)的研究区域中未包含干旱区,因此 SPEI在干旱区的适用性还有待检验。此外,Vicente-Serrano et al.(2010)选取的观测点中不包含中国区站点,所以SPEI在我国的适用性也需要进一步验证。本文旨在分析SPEI在我国不同等级降水区域的适用性,为这种新指数在我国推广应用提供参考。
2 资料与方法 2.1 资料本文所用资料来源于中国气象局整编的160个站1951~2010 年月降水和月平均气温资料。该资料是无缺值连续资料,在我国气候研究中已得到广泛认可和应用。
2.2 方法本文首先分析了多个时间尺度的SPEI在我国不同等级降水区域的适用性,然后对SPEI、SPI和H指数进行了比较分析。SPI和H的计算方法见Wu et al.(2007)和马柱国等(2005),下面给出SPEI的计算方法(Vicente-Serrano et al., 2010)。
首先,利用改进的Thornthwaite(1948)方法计算月潜在蒸发量PEj(单位:mm):
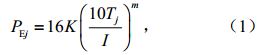


其中,j为月份,取1,…,12;Tj为月平均气温(单位:°C);Ij为月热量指数;I为年热量指数;常数m=0.492+1.79×10-2I-7.71×10-5I2+6.75×10-7I3,K为修正系数,计算公式为

其中,Ndm为该月总日数,N为可日照时数,计算公式为

其中
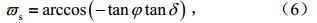
其中,

其中J是该月的平均日序,取值范围为[1,365]或[1,366],如1月1日取日序为1。
其次,构造不同时间尺度的累积水分亏缺量序列X,并计算其概率分布。某月的累积水分亏缺量为前k-1个月与当月水分亏缺量之和,k为时间尺度,k=1,...,48(McKee et al., 1993)。


其中,Pi为月降水量(单位:mm),Di为月水分亏缺量(单位:mm),i=1,...,n,n为时间序列的样本数。
引入三参数log-logistic概率分布函数计算累积水分亏缺量序列的概率分布。log-logistic概率密度函数为
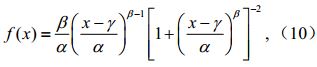
其中a、b和g 分别是尺度参数、形状参数和位置参数。b、a和g 分别由公式(11)~(13)计算
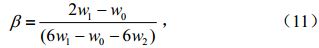
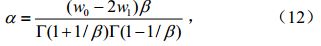
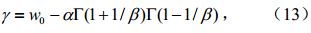
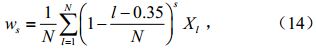
公式(14)中ws是概率权重矩(s=0,1,2),其中l是累积水分亏缺量序列X按升序排列(X1≤X2,···,≤Xn)的序数,N为样本总数,Γ(β)是Gamma函数。三参数log-logistic分布的 概率分布函数为

最后,对各月累积水分亏缺量序列的概率分布F(x)进行标准化处理。令P=1-F(x),当P≤0.5时,参数
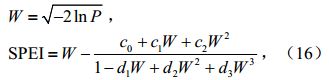
当P>0.5时,
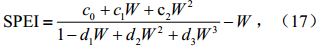
其中,c0 = 2.515517,c1 = 0.802853,c2 = 0.010328,d1 = 1.432788,d2 = 0.189269,d3 = 0.001308。 3 SPEI的适用性分析
SPEI的计算是基于这一假设:即某一时间尺度的累积水分亏缺量序列其概率分布服从log-logistic概率分布。因此,当某一时间尺度累积水分亏缺 量序列的经验概率分布与log-logistic概率分布近 似一致时,即认为该尺度SPEI分析适用于该序 列。为了检验SPEI在我国尤其是在干旱地区的适用性,在年均降水量(1981~2010年平均值)<100 mm、100~200 mm、200~300 mm、300~400 mm、400~600 mm、600~800 mm、800~1200 mm、>1200 mm的区域中各选取部分站点,对各站1、3、6、12、24、36个月多个尺度累积水分亏缺量序列的经验概率分布和log-logistic概率分布进行对比。
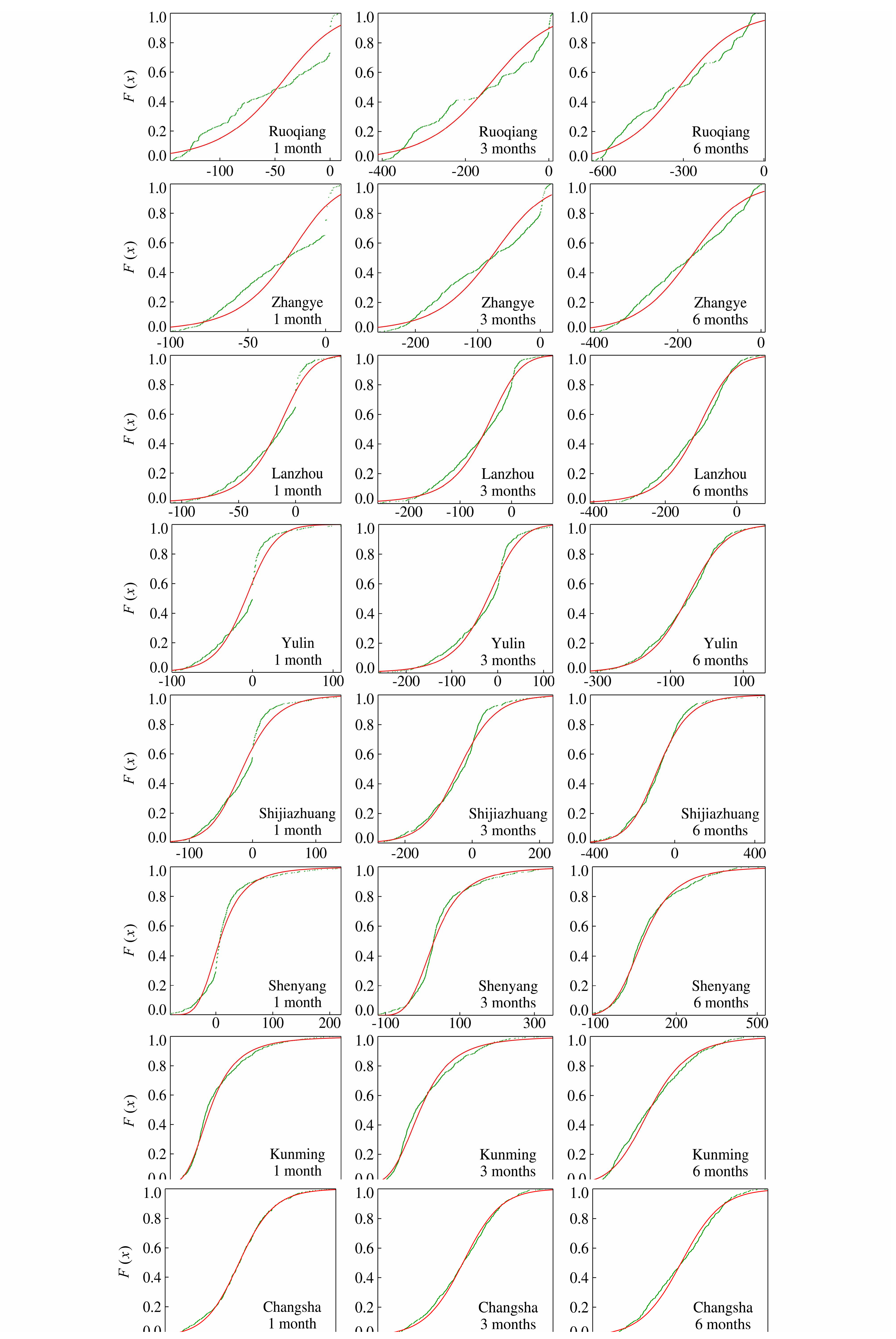
下面给出不同等级降水区域站点的具体分析:西北地区:若羌站(<100 mm)、张掖站(100~200 mm)和兰州站(200~300 mm);中部地区:榆林站(300~400 mm);华北地区:石家庄站(400~600 mm);东北地区:沈阳站(600~800 mm);西南地区:昆明站(800~1200 mm);东南地区:长沙站(>1200 mm)。1、3、6个月尺度累积水分亏缺量序列的概率分布曲线对比如图 1所示。图 1表明,在1个月尺度分析中,若羌站和张掖站水分亏缺量序列的log-logistic概率分布函数F(x)曲线和经验概率分布曲线的重合度较低,说明这两个站点1个月尺度的水分亏缺量序列不服从log-logistic概率分布;而兰州站、榆林站和石家庄站各自的曲线重合度较高,变化趋势比较一致,说明其1个月尺度的水分亏缺量序列近似服从log-logistic概率分布;沈阳站、昆明站和长沙站的曲线几乎完全重 合,说明其1个月尺度的水分亏缺量序列完全服从log-logistic概率分布。在3个月尺度分析中,除石家庄站3个月尺度的累积水分亏缺量序列由近似服从变为完全服从log-logistic概率分布外,其他站点3个月尺度的累积水分亏缺量序列概率分布情形与1个月尺度相似。在6个月尺度分析中,除兰州站和榆林站6个月尺度的累积水分亏缺量序列由近似服从变为完全服从log-logistic概率分布外,其他站点6个月尺度的累积水分亏缺量序列概率分布情形与3个月尺度相似。
|
图 1 1、3、6个月尺度log-logistic概率分布函数F(x)曲线(黑色)和经验概率分布曲线(灰色)对比 Fig. 1 Theoretical values according the log-logistic distribution(black line) and empirical(gray dots)F(x)values at the time scales of 1,3, and 6 months for the eight observatories |
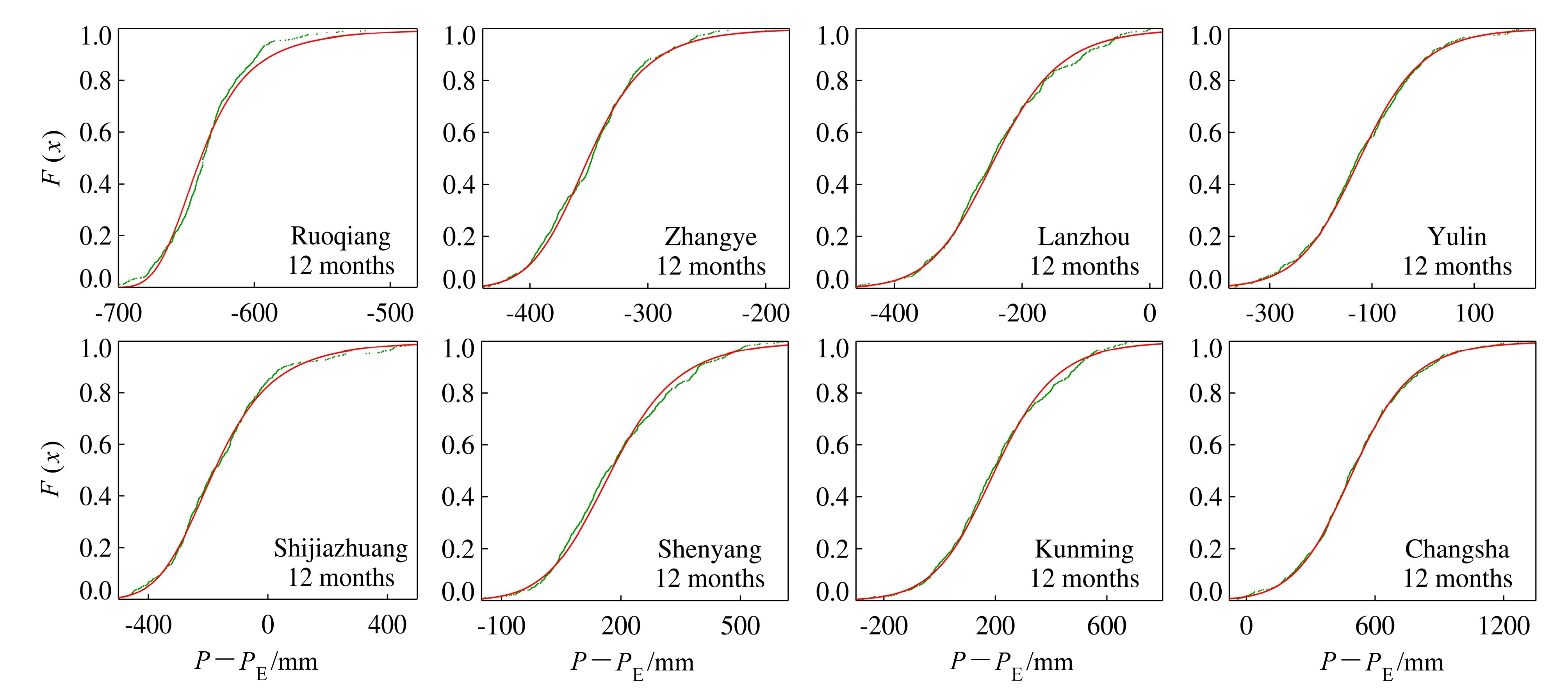
1 2个月尺度累积水分亏缺量序列的概率分布曲线对比如图 2所示。图 2表明,在12个月尺度分析中,各站的曲线重合度均很高,说明其12个月尺度的累积水分亏缺量序列完全服从log-logistic概率分布。24个月、36个月尺度分析与12个月尺度分析结果相同(图略)。通过对不同站点多个时间尺度分析对比可以得出,在干旱区(年均降水量小于200 mm),小于12个月的小尺度累积水分亏缺量序列概率分布均不服从log-logistic概率分布,即小于12个月的小尺度SPEI分析在该区不适用;而 在该区大于等于12个月的大尺度累积水分亏缺量序列概率分布则完全服从log-logistic概率分布,即大于等于12个月的大尺度SPEI分析在该区适 用;在降水量大于200 mm区域,各站小于12个月的累积水分亏缺量序列概率分布近似或完全服从log-logistic概率分布,大于等于12个月尺度的累积水分亏缺量序列概率分布完全服从log-logistic概 率分布,说明各种尺度的SPEI分析在该区均适用。通过不同时间尺度分析的对比发现,各站12个月尺度的累积水分亏缺量序列经验概率分布曲线与log-logistic概率分布曲线重合度均最高,说明12个月尺度的SPEI分析在各区适用性最好。
|
图 2 12个月尺度log-logistic概率分布函数F(x)线(黑色)和经验概率分布曲线(灰色)对比 Fig. 2 Theoretical values according the log-logistic distribution(black line)vs empirical(gray dots)F(x)values at the time scales of 12 months for the eight observatories |
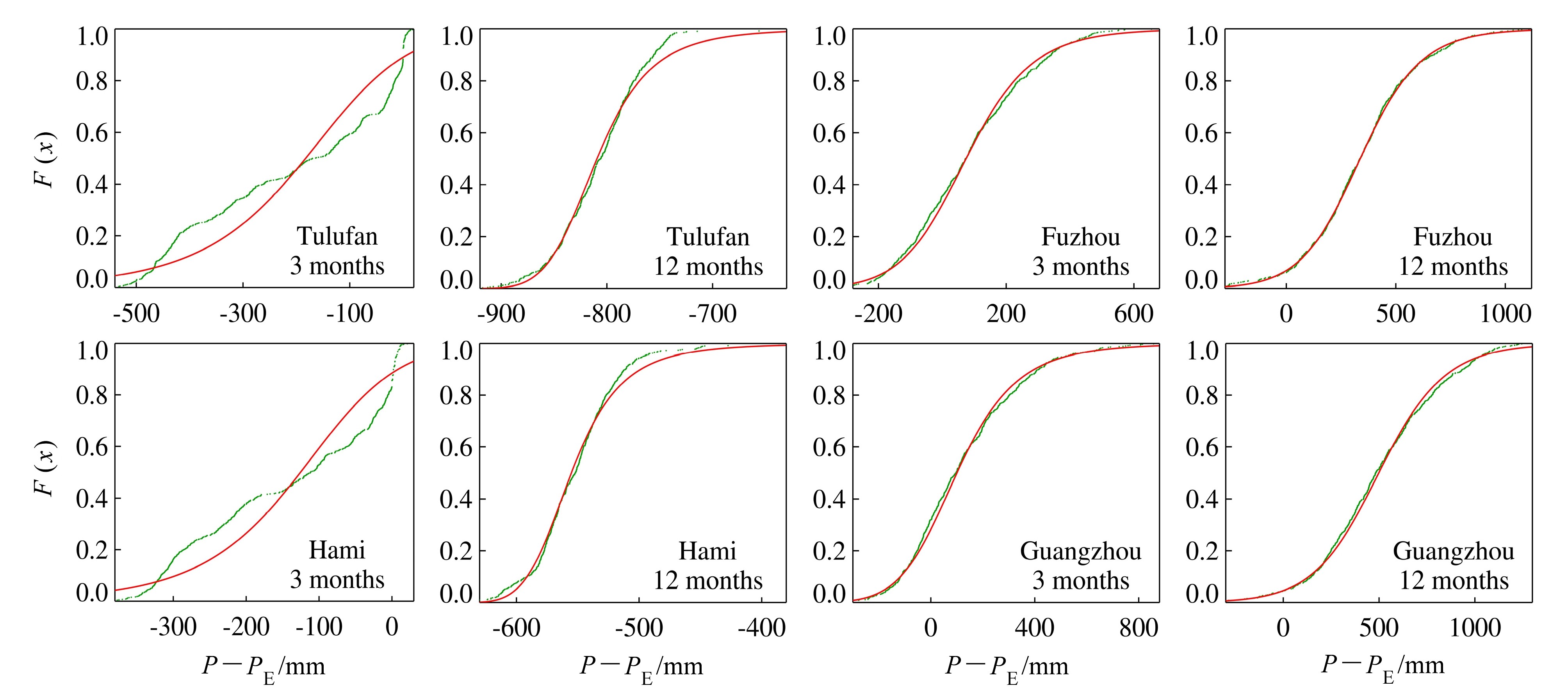
研究还发现,对于同一气候区的不同站点,相同尺度的SPEI分析其适用性是一致的(见图 3)。为了节约篇幅,只给出两个气候区4个站点对比结果,其他气候区及其他尺度分析所得结果相同。图 3为吐鲁番站、哈密站、福州站和广州站3、12个月尺度分析对比,其中吐鲁番站和哈密站属于干旱地区(<200 mm),福州站和广州站属于湿润地区(>1200 mm)。图 3显示,干旱地区两站3个月尺度SPEI分析均不适用,12个月尺度分析均适用;湿润地区两站3、12个月尺度分析均适用。
|
图 3 3、12个月尺度log-logistic概率分布函数F(x)线(黑色)和经验概率分布曲线(灰色)对比 Fig. 3 Theoretical values according the log-logistic distribution(black line) and empirical(gray dots)F(x)values at the time scales of 3 and 12 months for the four observatories |
综合以上分析得出,在我国降水量大于200 mm区域各种尺度SPEI分析均可适用,在干旱区只有大于12个月的大尺度SPEI分析适用较好,其中12个月时间尺度的SPEI分析在各区适用性最好;而在分析干旱区1、3、6个月的小尺度干旱时不建议使用SPEI。
对于在干旱区小于12个月的小尺度SPEI分析不适用的原因,将从SPEI的数学基础和物理意义两方面进行讨论。
首先,从SPEI计算公式的数学基础上分析,对该区小尺度累积水分亏缺量序列的log-logistic概 率密度和经验概率密度进行对比。若羌站和张掖站1、3个月尺度累积水分亏缺量序列概率密度如图 4。图 4显示,两站1、3个月尺度累积水分亏缺量序列的log-logistic概率密度函数f(x)对经验概率密度的拟合效果均较差,两站1、3个月尺度累积水分亏缺量序列经验概率密度均在0值附近异常偏高。该区6个 月尺度概率密度对比分析结果与3个月尺度相似。对两站降水和气温资料分析后认为,由于两站每年11月至次年2月平均气温常低于0 °C,潜在蒸发量为 0,而同期降水稀少,致使小尺度月累积水分亏缺量0值附近概率异常偏高,从而导致概率分布异常,降低了SPEI在该区小尺度分析中的可适用性。
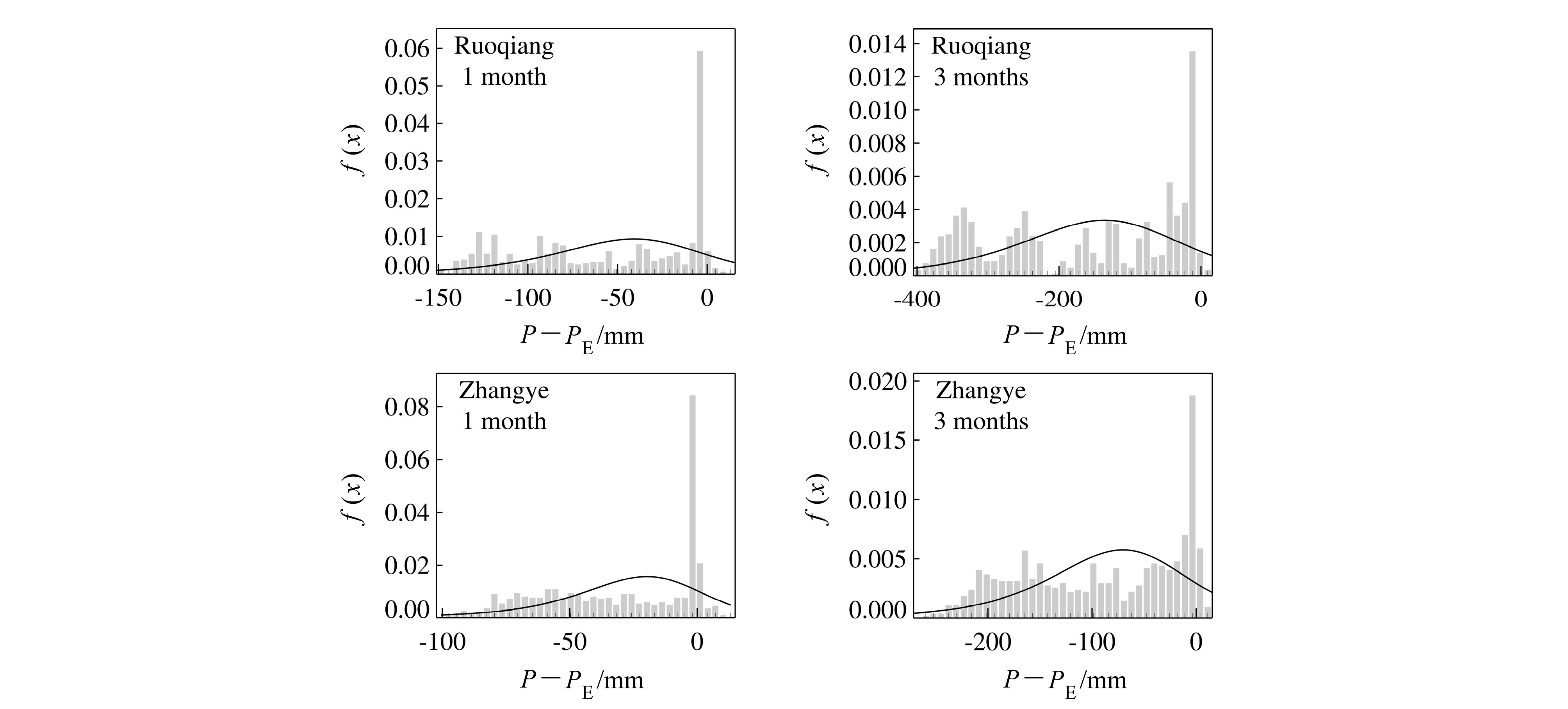
|
图 4 若羌站和张掖站 1、3个月尺度经验概率直方图(灰色)和log-logistic概率密度函数f(x)曲线(黑色)对比 Fig. 4 Empirical(grey) and modeled(black)f(x)values using the log-logistic distributions at the time scales of 1 and 3 months at Ruoqiang and Zhangye observatories |
其次,从物理意义上看,如图 4所示,在我国干旱区,水分亏缺量处于负值区的频率远大于正值区。这表明该区地表水分经常处于输出状态,且输入量远小于输出量。由物质守恒定律可知,地表水分不可能长期处于这种不平衡状态即输出状态。导致这种情况的可能原因有二:一是计算地表水分的输入时未考虑其他影响较大的源,如地表径流等;二是通过Thornthwaite(1948)方法计算得到的地表水分输出值即潜在蒸发量偏大,这涉及到使用Thornthwaite(1948)方法计算潜在蒸发量在干旱区的适用性问题。这些问题已超出本文研究的范围,将在后续工作中做更深入的研究。
4 SPEI与SPI、H 指数对比分析SPI和H指数是我国干旱研究中应用较为成熟的指数,通过比较SPEI与这两个指数在不同区域进行干旱分析中的异同,可以突显SPEI在表征干旱程度上的优越性。由于H指数只有年际尺度,仅能反映干湿变化趋势,因而在此重点比较SPEI和SPI的异同。为了便于对比,采用近于年际尺度的12个月SPEI和SPI序列进行分析。在干旱地区(降水量显著小于蒸发量)和湿润地区(降水量显著大于蒸发量)各选取一个站点,分别为张掖站和长沙站,比较其H指数、12个月尺度的SPEI和SPI序列。
张掖站12个月尺度的SPEI和SPI、H指数及年均气温序列如图 5。图 5表明,张掖站12个月尺度的SPEI 序列在60年代以前呈下降趋势,60~80年代呈上升趋势,80年代初至90年代中期处于大幅震荡中,在1997年以后出现大幅下降,部分SPEI值低于-2,表明该站所在地区在1997~2004年期间发生了几次极端干旱,之后的变化显示,旱情在2005年以后得到了缓解;12个月尺度的SPI 序列在60年代以前呈下降趋势,60~80年代呈上升趋势,80年代初至90年代中期处于大幅震荡中,在1997年以后未出现明显下降,2000年以后呈上升趋势,2005年以后呈明显上升趋势;H指数序列的变化趋势与SPEI序列总体趋势一致。
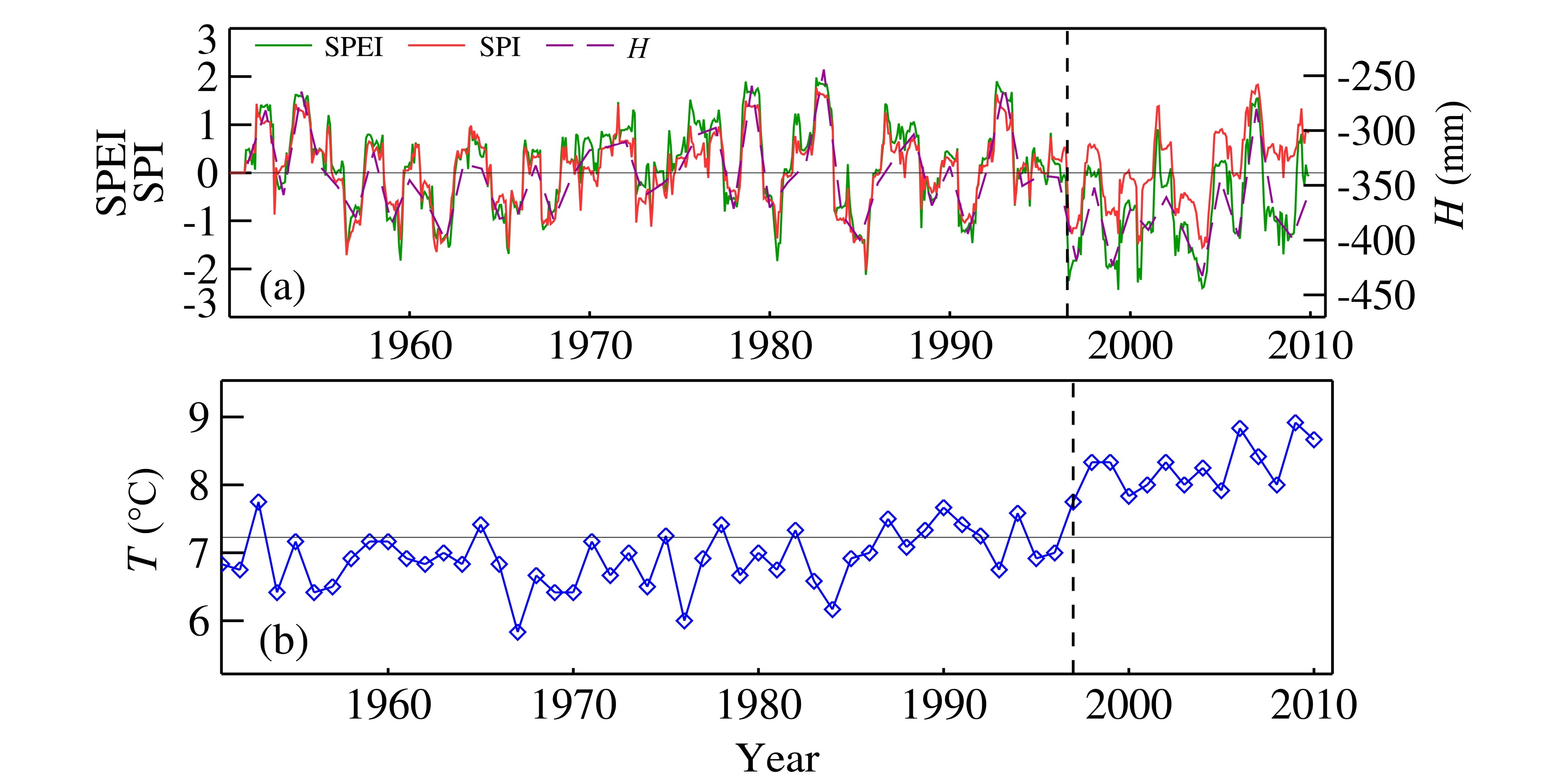
|
图 5 张掖站(a)12个月尺度SPEI、12个月尺度SPI、H指数及(b)年均气温1951~2010年时间序列 Fig. 5 The(a)12-month SPEI,12-month SPI, and H index and (b)annual temperature during 1951–2010 at Zhangye observatory |
对比发现,12个月尺度的SPEI和SPI序列在70年代以前变化几乎完全相同;70年代以后变化趋势一致,只是SPEI序列振幅略大于SPI;自1997年以后,SPEI序列变化趋势与SPI序列发现明显差异,SPEI值表明发生严重干旱,而SPI值显示轻度干旱,对比同期H指数,发现H指数值处于历史最低值附近,说明SPI未能真实反映这一时段的干旱严重程度;2005年以后,SPI序列呈现出明显的变湿趋势,而SPEI序列只是呈现弱的变湿趋势,H指数序列的变化趋势与SPEI相似,说明SPI对该时段干湿变化的表征已出现明显偏差。
对比气温序列变化发现,该站气温在1997年发生明显跃变,之后持续在高位震荡,即该区自1997年以后明显变暖。由此得出,在降水量显著小于蒸发量的地区,增温引起的干旱化确实加剧了 这些地区的干旱程度。而SPI只包含降水变化信息,不能反映气温的影响,难以表征真实干旱程度。
长沙站12个月尺度的SPEI和SPI、H指数及年均气温序列如图 6。图 6表明,长沙站12个月尺度的SPEI和SPI序列与同期H指数序列变化趋势一致,只是在1997年以后SPEI的低值点低于同期的SPI值。同期气温序列变化显示,该站所在地区气温在1997年也发生明显跃变,由此说明,在降水量显著大于蒸发量的地区,增温对干旱程度影响还比较有限。
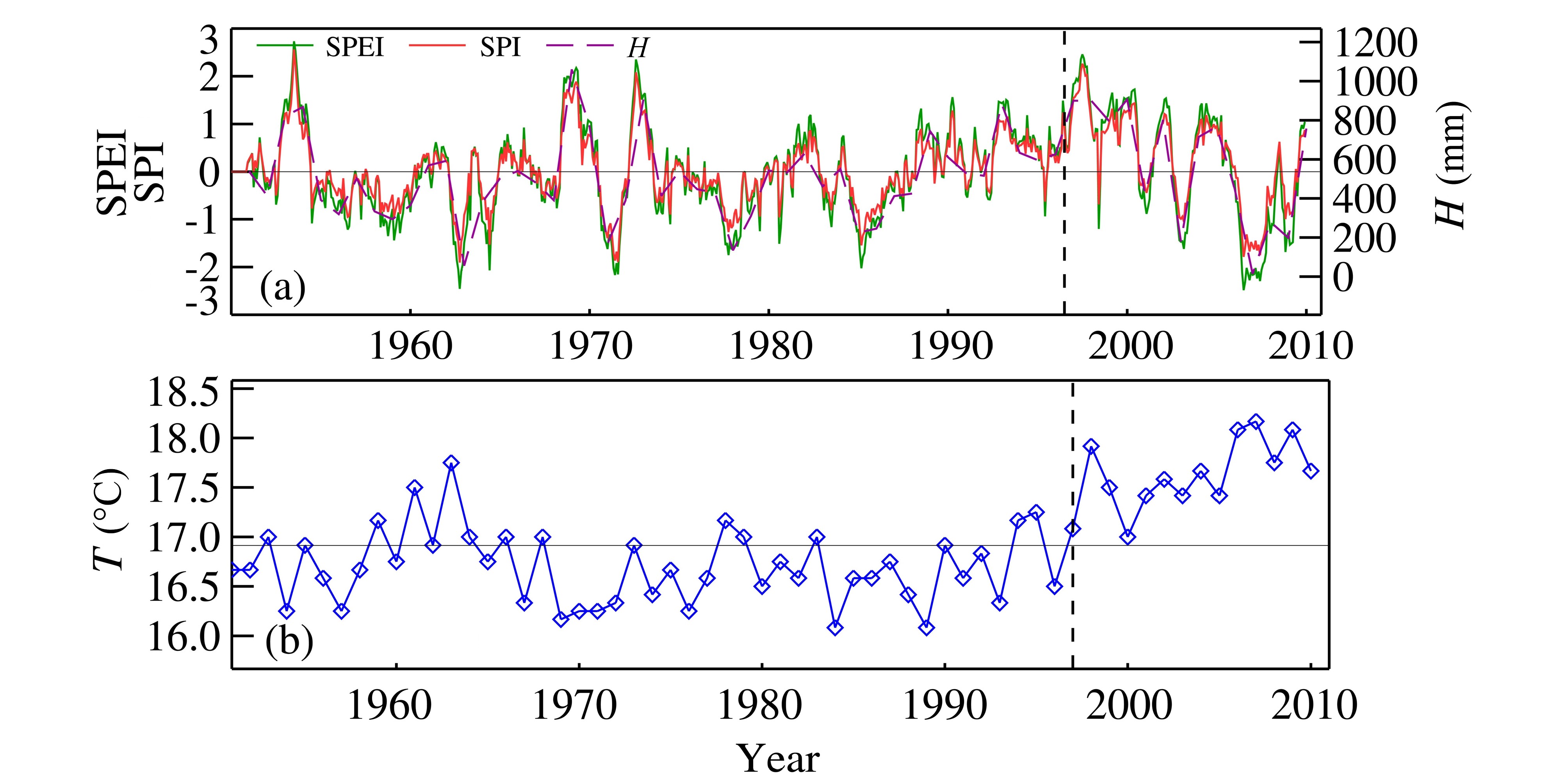
|
图 6 同图 5,但为长沙站 Fig. 6 Same as Fig. 5,but for Changsha observatory |
通过对比发现,SPEI序列与H指数序列在干旱地区与湿润地区均呈现一致变化趋势,说明SPEI能充分反映增温效应对干湿变化的影响;而SPEI与SPI序列只在湿润区和1997年以前的干旱地区呈现一致变化趋势,说明 SPI已不能较好地反映我国1997年气温跃变以来干旱地区干旱程度的新变化,而在湿润地区,SPI仍是一种较为有效的干旱指数。H指数虽能反映增温对干湿变化的影响,但只能反映年际尺度的趋势变化,无法作为一种监测指数识别干旱的发生与结束。
5 结论通过对SPEI计算方法的介绍并检验其在我国不同气候区的适用性,以及对SPEI、SPI与H指数的比较分析,得到主要结论如下:
(1)在我国年均降水量大于200 mm区域各种尺度SPEI分析均可适用,在干旱区只有大于12个月的大尺度SPEI分析适用较好,其中12个月时间尺度的SPEI分析在各区适用性最好。
(2)在年均降水量小于200 mm的干旱区,由于冬季月平均气温常小于等于0 °C,潜在蒸发量为0,且降水稀少,导致小于12个月的小尺度累积水分亏缺量序列0值附近概率异常偏高,不服从log- logistic概率分布,降低了SPEI在该区小尺度分析中的可适用性。所以,在分析我国干旱区1、3、6个月小尺度干旱时不建议使用SPEI。
(3)与SPI和H指数相比,SPEI在干旱区和湿润区均能充分反映增温引起的干旱程度的变化,并可作为监测指数识别干旱是否发生或结束,能较准确地表征干旱状况。
(4)1997年气温跃变以后,干旱区的干旱程度有所加剧,而只包含降水信息的单因素指数SPI不能反映这种变化;气温跃变对湿润区的影响尚不明显。
| [1] | Guttman N B. 1998. Comparing the Palmer drought index and the standardized precipitation index[J]. Journal of the American Water Resources Association, 34 (1): 113-121. |
| [2] | Hayes M, Wilhite D, Svoboda M, et al. 1999. Monitoring the 1996 drought using the standardized precipitation index[J]. Bull. Amer. Meteor. Soc., 80 (3): 429-438. |
| [3] | Ji L, Peters A J. 2003. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices[J]. Remote Sens. Environ., 87 (1): 85-98. |
| [4] | 马柱国, 黄刚, 甘文强, 等. 2005. 近代中国北方干湿变化趋势的多时段特征[J]. 大气科学, 29 (5): 671-681. Ma Zhuguo, Huang Gang, Gan Wenqiang, et al. 2005. Multi-scale temporal characteristics of the dryness/wetness over northern China during the last century[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 29 (5): 671- 681. |
| [5] | McKee T B, Doesken N J, Kleist J. 1993. The relationship of drought frequency and duration to time scales[C]./Proceedings of the Eighth Conference on Applied Climatology. Boston, MA: American Meteorological Society, 179-184. |
| [6] | McKee T B, Doesken N J, Kleist J. 1995. Drought monitoring with multiple time scales[C].//Proceedings of the Ninth Conference on Applied Climatology. Boston, MA: American Meteorological Society, 233-236. |
| [7] | Palmer W C. 1965. Meteorological droughts[C].//US Department of Commerce Weather Bureau Research Paper, 45-58. |
| [8] | Thornthwaite C W. 1948. An approach toward a rational classification of climate[J]. Geographical Reviews, 38 (1): 55-94. |
| [9] | Vicente-Serrano S M, Beguería S, López-Moreno J I. 2010. A multi- scalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index—SPEI[J]. J. Climate, 23: 1696- 1718. |
| [10] | Wu H, Svoboda M, Hayes M, et al. 2007. Appropriate application of the standardized precipitation index in arid locations and dry season[J]. International Journal of Climatology, 27: 65-79. |
| [11] | 周后福, 方茸, 张建军, 等. 2010. 基于SVD 和修正Z 指数的汛期旱涝预测及其应用[J]. 气候与环境研究, 15 (1): 64-72. Zhou Houfu, Fang Rong, Zhang Jianjun, et al. 2010. Predict ion for drought/flood during the flood season based on SVD method and modified Z index and its application[J]. Climatic and Environmental Research (in Chinese), 15 (1): 64-72. |
| [12] | 邹旭恺, 任国玉, 张强. 2010. 基于综合气象干旱指数的中国干旱变化趋势研究[J]. 气候与环境研究, 15 (4): 371-378. Zou Xukai, Ren Guoyu, Zhang Qiang. 2010. Droughts variations in China based on a compound index of meteorological drought[J]. Climatic and Environmental Research (in Chinese), 15 (4): 371-378. |
 2013,Vol. 18
2013,Vol. 18

