平均降水量是天气、气候、水文和遥感等诸多领域常用的特征量，其计算和应用是一个复杂的科学问题。某地域在特定时段的平均降水量定义式(王名才，1994)为：

其中，p为连续分布的点雨量，c是点雨量所代表的面积，A_c是区域面积。但是，降水量的观测并不是连续分布，而是离散的，若有N个观测值p_i(i=1，2，…，N)，那么(1)式可写成离散形式：

(2)式也可写为：

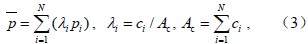
其中，λ_i为第i个观测值p_i的权重系数，显然，N值越大，由(2)式算出的结果就趋近于(1)式，因此，平均降水量的估算分为空间分析方法研究和观测技术研究两个方向；观测技术研究是通过卫星、雷达或其他非常规观测技术获得更为精细的降水量资料，本质上是提高(2)、(3)式中的N值，观测技术研究目前还有许多难题尚待解决；空间分析方法是平均降水量计算的基础，大致有算术平均法、V图法、三角形法、垂直平分法、等雨量线法、地统计学法等，算术平均法、垂直平分法、等雨量线法在流域平均雨量中应用较多；垂直平分法是将各相邻的雨量站直线相连，作各连线的垂直平分线，将流域划分成若干多边形；等雨量线法则是对于较大的流域，首先绘制等雨量线图，量出相邻等雨量线间的面积，以等雨量线间的平均雨量为该面积上的雨量。各种空间分析方法的差别主要体现在对(3)式中λ_i数值大小的影响，从而有不同的计算结果。

目前，对于大区域、较长时间序列的平均降水量的计算通常使用算术平均法，根据(3)式，算术平均法下各个观测站的权重系数λ_i都是相等 的，但实况观测站并非均匀分布，也就是说λ_i应该是变化的，因此，有必要通过更为合理的计算方法获得趋于客观的数值。Thiessen(1911)根据观测站点的降水量分布，讨论了以各站点代表的面积大小确定权重系数，分析了较小区域中有限点V图构造及平均降水量计算方法；Henry(1980)根据气候特点把阿拉斯加州(Alaska)划分成若干个小区域，并以每个小区域的面积除以总面积后的值作为权重系数，使用站点的观测，求出1931～1977年阿拉斯加州月(年)平均降水量；国内也有研究者使用泰森多边形法计算流域的面雨量(方慈安等，2003)；但是以上基于几何多边形确定λ_i方法缺乏严格的数学定义和完备的算法，起源于20世纪70年代的计算几何学为平均降水量提供了理论基础和算法实现，本文将使用区域Delaunay三角剖分法计算全国平均降水量。

使用1980年1月1日至2009年12月31日的全国2200个观测站点的24 h降水量资料，首先构建区域Delaunay三角网，然后计算三角片的面积，最后根据(3)式求得全国平均降水量。

Delaunay三角插值具有严格的数学定义和完备的理论基础；它起源于Voronoi图(简称V图)，1850年Dirichlet讨论了V图概念；Voronoi G于1908年在数学上定义了V图，V图主要用于分析空间点集或者其他几何对象和距离有关的问题；1934年，B. Delaunay在分析V图的基点间直线嵌入时，首次提出了Delaunay三角网络概念；1975年，Shamos和Hey讨论了使用计算机有效地构建V图，标志 着计算几何的诞生，V图和Delaunay三角网是计算 几何的重要基石。

Delaunay三角网是V图的对偶图，具有两个重要特性：(1)空外接圆性质：在点集P构建的Delaunay三角网中，每个三角形的外接圆中均不包含点集 P中其他任意点，即任意4点不共圆。(2)最大化最小角性质：三角网中每个三角形的角度尽可能最大，就是说，在两个相邻三角形构成的四边行中，当变换四边形的对角线时，6个内角的最小角不再增大，并且使三角形各边尽量接近等边。

根据上述性质，Delaunay三角剖分是最优的三角剖分，具有广泛的应用价值，也常用来作为其他三角剖分算法的初始剖分；Miles(1969)证明Delaunay三角网是性能优秀的三角网；Sibson(1978)认为在一个有限点集中，只存在一个局部等角的三角网，也就是Delaunay三角网；Lingas(1986)证明了Delaunay三角网是最优的；Tsai(1993)认为，在不多于3个相邻点共圆的欧几里德平面中，Delaunay三角网是唯一的。

Delaunay三角网构成的多边形属于凸集，但是中国陆地区域的外边界是凹集，如果直接使用Delaunay三角剖分，那么将有较多的三角形出现在中国区域之外；因此，针对凹集或者其他更复杂的多边形，需要采取区域Delaunay三角剖分法，使所得到的Delaunay三角网限定在研究的区域之内，由此可见，所谓区域Delaunay三角剖分法是指有限定条件的Delaunay三角剖分，其实现原理和普通的Delaunay三角剖分法大致相同，只是额外增加了限定条件并在原有算法基础上付诸实现。

经过多年的发展，Delaunay三角网生成算法已经趋于成熟，大致可以分成三类：分治算法、三角网生长法和随机增长法。

分治算法：基本思路是首先对原始数据点集进行递归分割成更容易实现三角化的子集，对每个子集进行三角剖分，并用局部优化(LOP，Local Optimization Procedure)算法进行优化，保证三角剖分为Delaunay三角网，然后，寻找每个子集凸壳的底线和顶线，由底线到顶线自下而上的合并，最终完成整个数据点集的三角形网络。

三角网生长法：从一个起始点开始，逐步形成覆盖整个点集的三角网，有两种趋势相反的生长过程，划分为扩张生长法和收缩生长法；扩张生长法是首先以点集中任一点为源，寻找和起始点距离最短的另一点，并连接两点产生初始三角片的一条边，然后使用判别准则搜索包含此边的另一个顶点，依次类推，向外层层推展，最后形成覆盖整个区域的三角网；收缩生长法，正好相反，先在数据点集的最外边界生成凸壳，以此为源，向内扫描逐步缩小并形成整个三角网。

3种生成算法各有优缺点，随机增长法较容易实现，占有内存小。本文将采用随机增长法进行Delaunay三角剖分(熊敏诠，2012)，基本步骤如下：

步骤一：在区域外边界上根据周边站点分布选取边界点，由边界点和观测站共同构成的点集P；另外再设置3点，令其连线形成的三角形能覆盖整个点集P，同时确保这3点不在点集P中任意3点的外接圆之中。

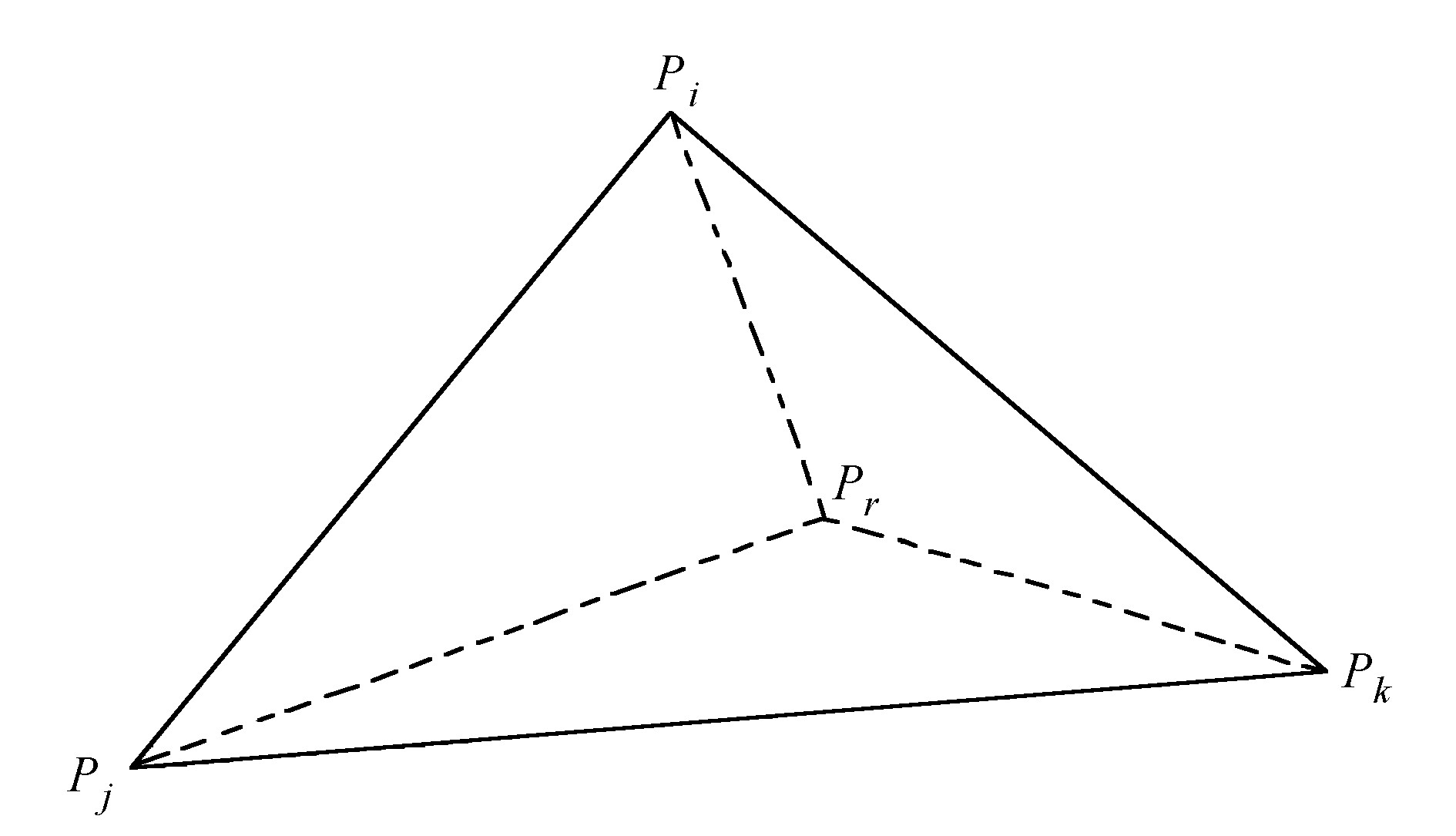
步骤二：从P中随机抽取任意点P_r，分析其和当前的三角形位置关系(如图 1)；若P_r位于ΔP_iP_jP_k内部，那么将P_r和ΔP_iP_jP_k的3个顶点建立连线，那么就形成新的边及其三角形；若P_r恰好落在ΔP_iP_jP_k的某条边上，那么将该边对应两个三角形顶点和P_r及该边的两端点连接，形成新的三角形。

图 1 新增点Pr位于ΔPiPjPk Fig. 1 New point Pr in the ΔPiPjPk

步骤三：得到新的三角剖分后，对非法边不断翻转，直到其满足Delaunay三角条件，成为合法边；因此需要不断地递归调用判据，实现当前Delaunay三角网的更新和维护。

步骤四：重复步骤二、步骤三，直到完成对所有点的Delaunay三角剖分。

步骤五：删除步骤一中初始添加的3点及其关联的边；删除边界上的离散点和其相关联的边。

上述5个步骤中有两个重要判别式需要列出。图 1显示了在步骤二中需要判断点P_r在ΔP_iP_jP_k中的位置，使用矢量叉积法分析，其表达式：

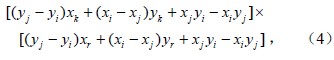
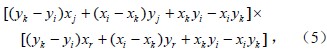
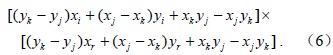
其中，x、y及其下标i、j、k分别表示三角平面上P_i、P_j、P_k各点对应的空间位置；当(4)–(6)式的计算结果均大于0，表示点P_r位于ΔP_iP_jP_k中；若3个数值至少有1个负数，那么P_r在ΔP_iP_jP_k之外；若3个值出现有零，那么P_r在ΔP_iP_jP_k某条边或顶点上。

步骤三必须判断每条边是否符合Delaunay三角条件，其判据如下(Leonidas and Jorge， 1985)：

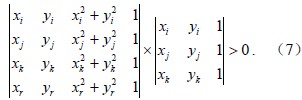
若满足(7)式，则P_r在ΔP_iP_jP_k外接圆内，需要通过对非法边的翻转直到符合Delaunay三角条件。

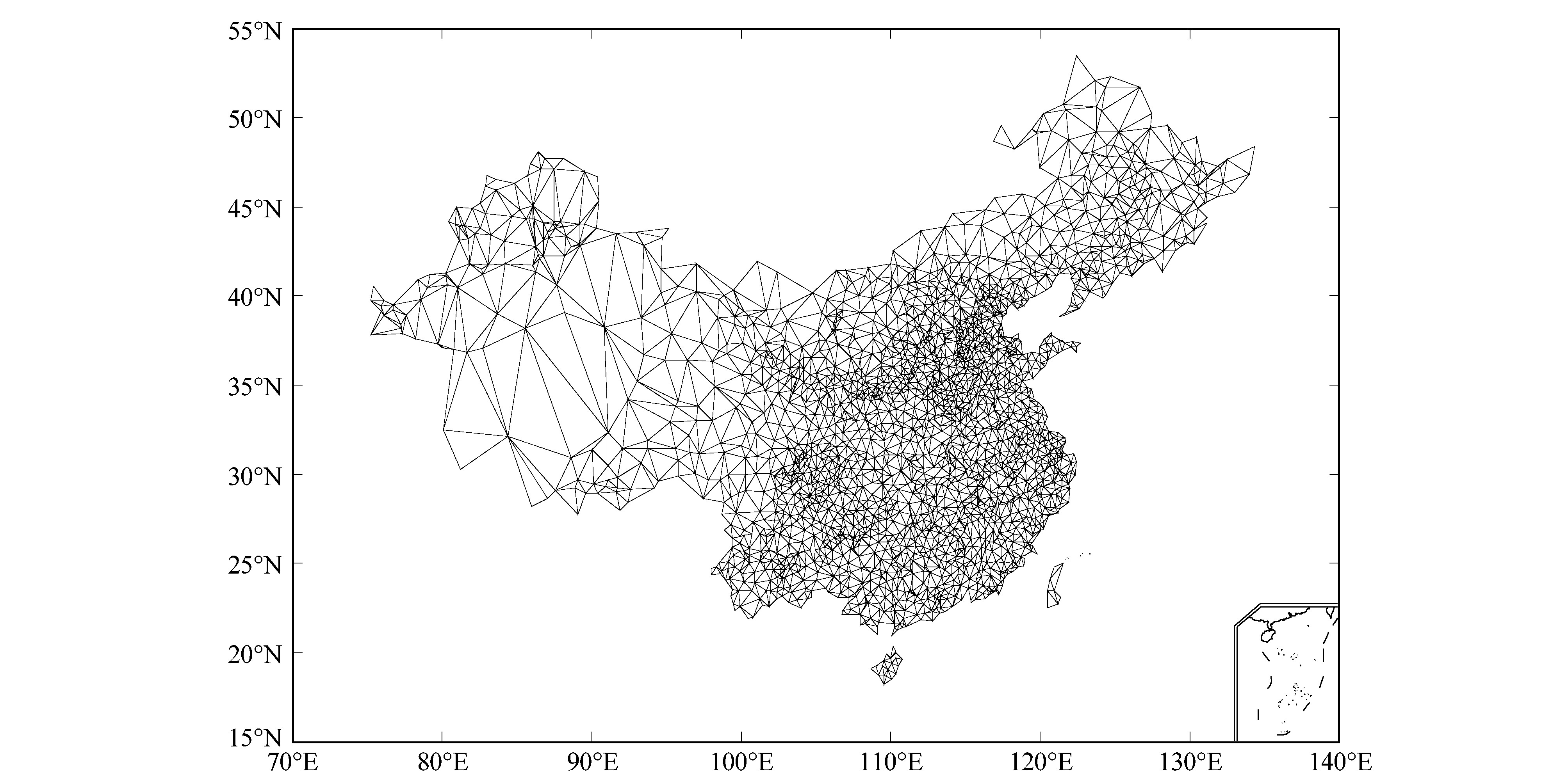
使用随机增长法，对全国陆地观测站进行区域的Delaunay三角剖分，如图 2所示，实现了较为理想的区域Delaunay三角网，其中，每个三角形的顶点都对应有观测站点。

图 2 根据全国2200个观测站的区域Delaunay三角剖分图 Fig. 2 Constrained delaunay triangulation of 2200 observation stations in China

通过Delaunay三角剖分后，在椭球面上得到以观测站点为顶点、由大地线组成的三角网，大地线是一条空间曲线，在椭球面上该曲线的各点曲率各不相同，因而要求解椭球上的三角形将十分复杂。基于Delaunay三角的平均降水量的研究和应用中需要考虑计算结果要有足够精度，同时计算过程简洁、高效；研究表明(陈健和晁定波，1989)，由于地球的扁率很小(大约0.003)，将地球表面上边长小于200 km的三角形和球面上的等角投影三角形进行比较，椭球面三角形与球面三角形对 应角的差异小于0.001"，边长的和差异小于1 mm，因此可以用球面三角形代替椭球面三角形进行解算。

球面三角面积公式属于球面几何内容，作为平均降水量较重要的步骤，下文简要地给出了推导。

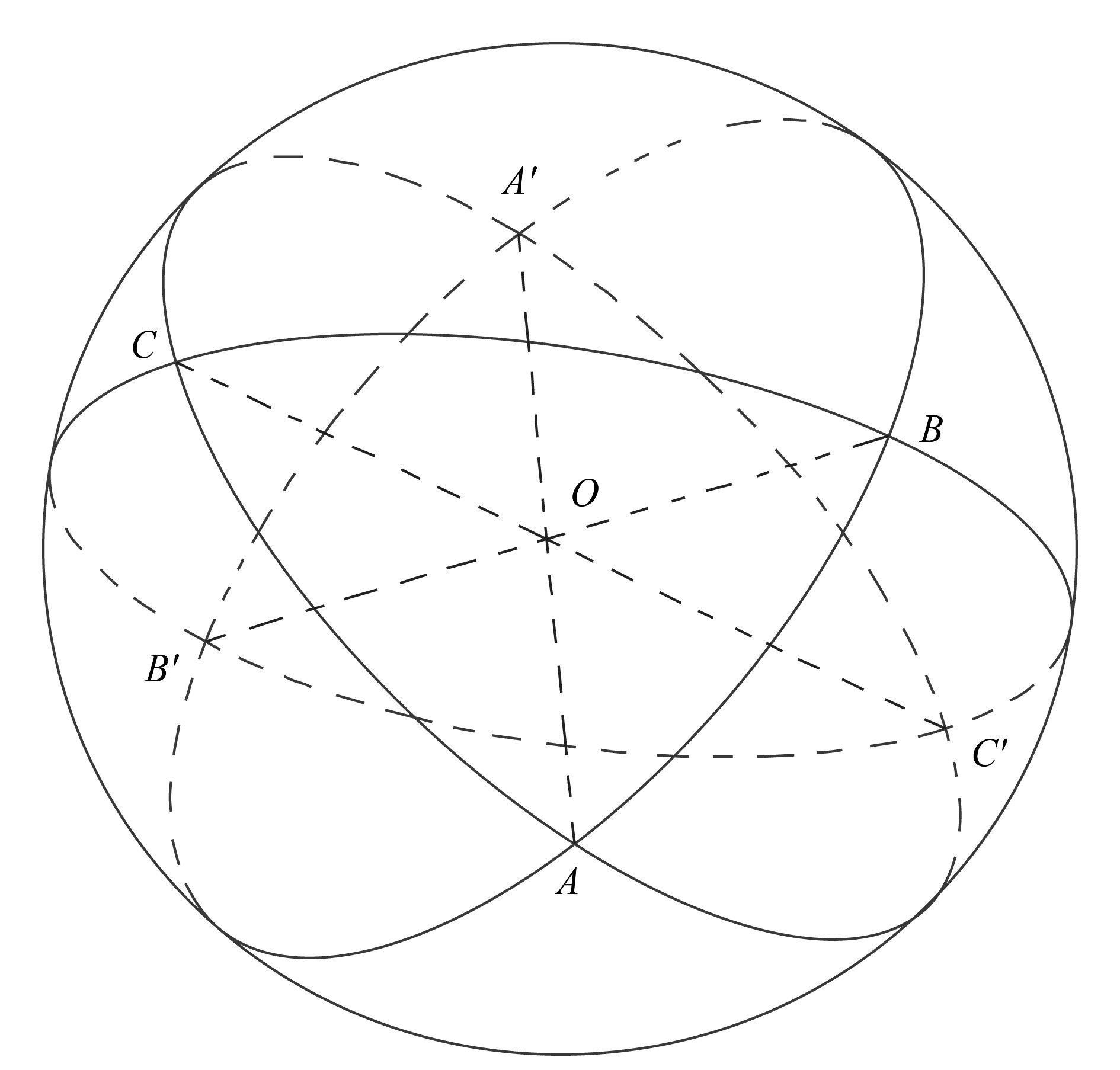
如任意球面三角形ABC，将其各边分别延长(图 3)，就形成3个球面二角形：C–AA'–B、C–BB'–A、A–CC'–B，根据球面三角学定理，球面二角形的面积(S)为：S=(x/90)πR²，其中x为球面二角形的夹角，R是半径。三角形的角度为A、B、C，可得：

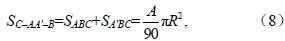
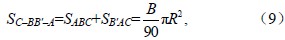
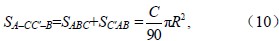
其中，S_C–AA'–B、S_C–BB'–A、S_A–CC'–B、分别表示球面二角形C–AA'–B、C–BB'–A、A–CC'–B的面积，S_ABC、S_B'AC、S_C'AB分别表示球面三角形ABC、B'AC、C'AB的面积。

图 3 球面三角形ABC示意图 Fig. 3 Spherical triangle ABC schematic

根据对顶角和半径的关系：∠BOA'=∠B'OA、∠COA'=∠C'OA、∠BOC=∠B'OC'、OC=OC'、OB=OB'、OA=OA'，所以球面三角形CBA'和C'B'A、B'AC和A'C'B、C'AB和A'B'C、ABC和A'B'C'两两对称，且面积相等，(8)、(9)、(10)式相加，得到：

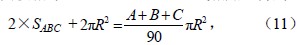
即：

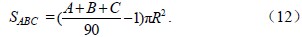
以上是在球坐标系中，得到了球面三角形的面积表达式；那么，只要知道三个内角的大小，就可以计算面积；但是在球坐标系中直接估算角度比较复杂，本文将在空间直角坐标系中求角度。由于已知量是观测站点的经纬度，这是大地坐标系上的空间位置，必须转换到以地球参考椭球的中心为原点的空间直角坐标系，其Z轴与地球自转轴平行并指向参考椭球的北极，X轴指向参考椭球的本初子午线，Y轴与X轴和Z轴相互垂直构成一个右手系。地球半径R_g，站点在大地坐标系中的经度Φ、纬度θ，大地坐标系到空间直角坐标系的转换公式如下：

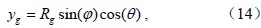
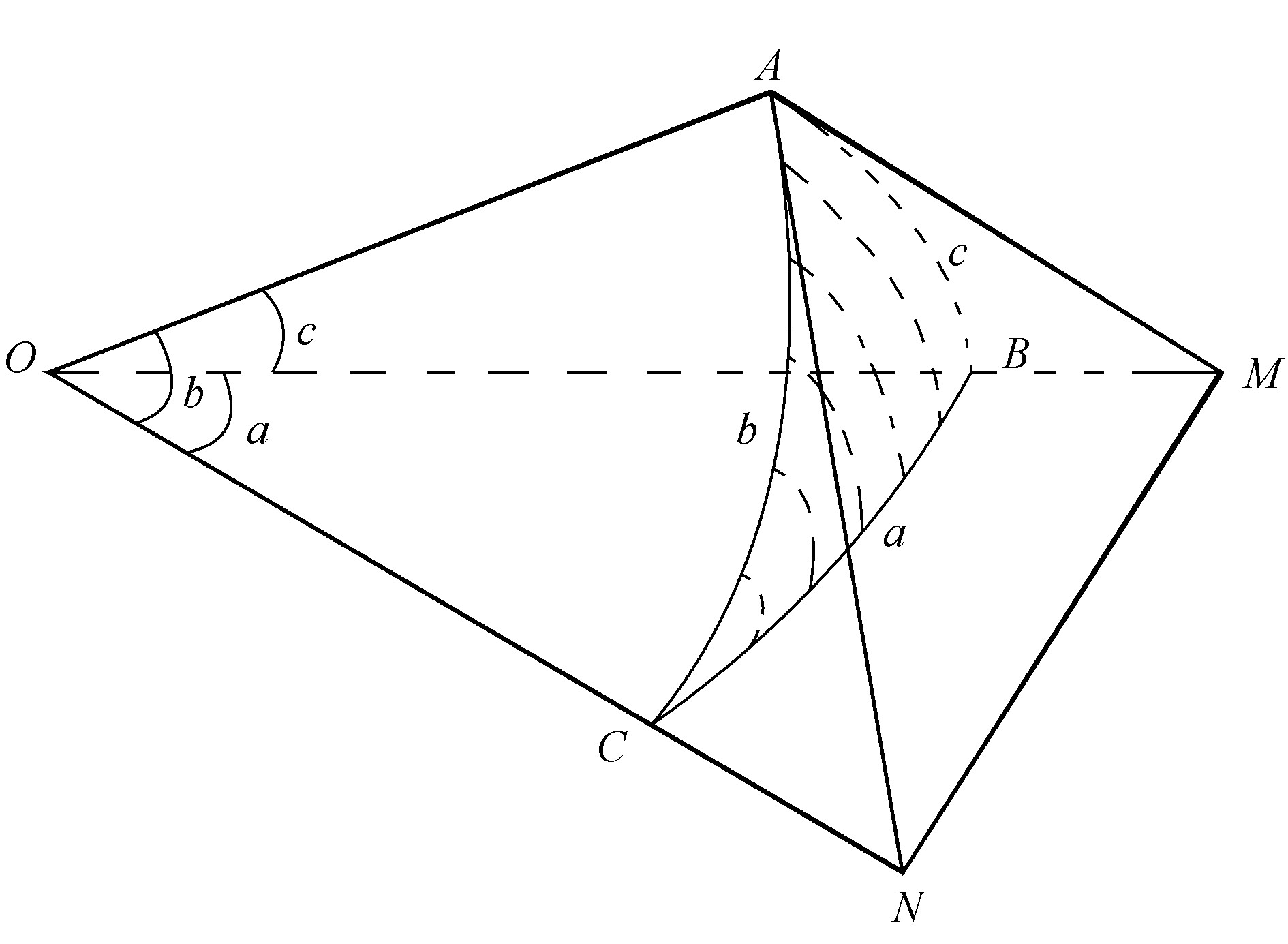
将空间直角坐标系的原点O和球面三角形ABC的顶点相连，可得一球心三面角O–ABC(图 4)过顶点A 做b、c 边的切线，分别交OC，OB 的延长线于N、M，由此得到两个平面直角三角形△OAM、△OAN和两个平面普通三角形△OMN、△AMN。

图 4 球心三面角O–ABC示意图 Fig. 4 Spherical trihedral corner O–ABC schematic

在平面三角形△OMN 中，应用平面三角的余弦定理(推导略)，得到a边的余弦公式：

同理，b边和c边的余弦公式：

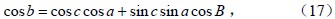
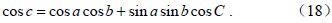
由(16)–(18)式，可以得到球面三角形的内角：

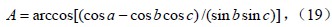
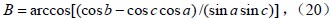
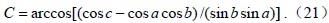
而球心三面角O-ABC中的夹角a、b、c，就可以通过向量的直角坐标运算求得，其中，点A(x₁,y₁,z₁)、B(x₂,y₂,z₂)、C(x₃,y₃,z₃)。

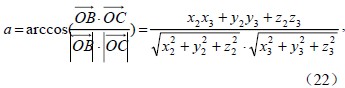
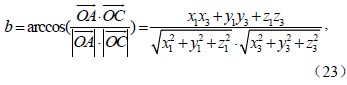
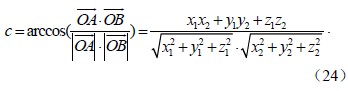
当要计算某个时刻或时段内降水量全国平均值，往往采用算术平均法(以下称为方法一)，那么本文将其计算所得的平均降水量和区域Delaunay三角剖分法(以下称为方法二)进行比较。

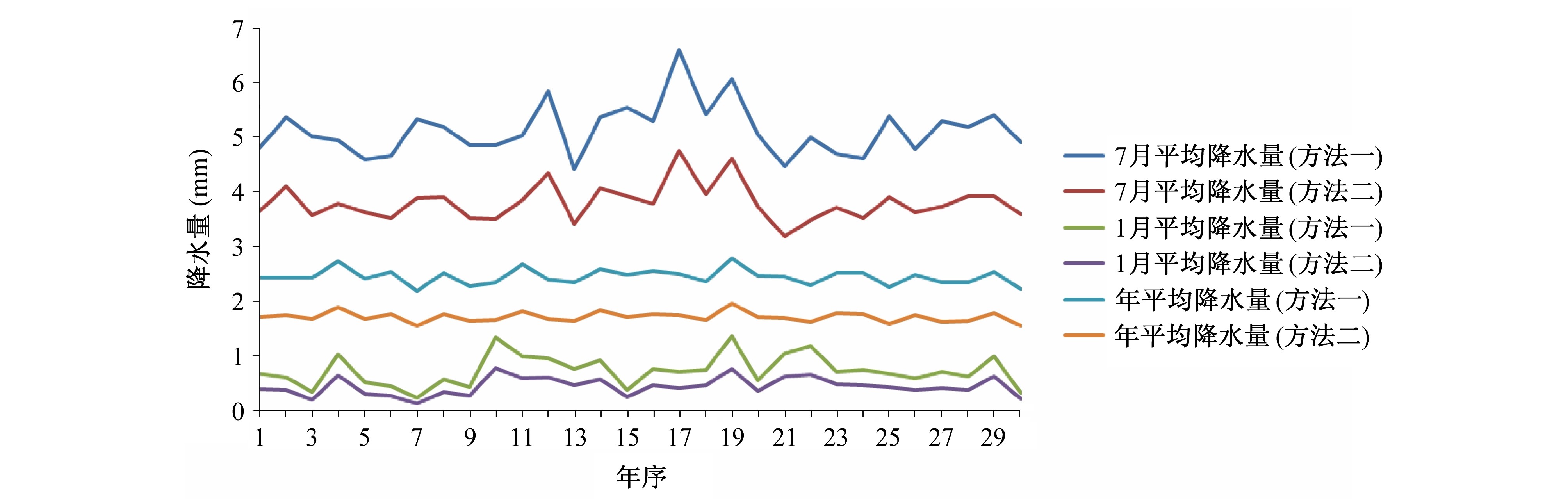
两种方法计算结果有较大差异(表 1)：方法一的全国平均降水量的均值都大于方法二对应值，大致达到了1.4倍；标准偏差是度量样本值的分散程度，方法一相应的标准偏差值也偏大。两方法计算结果间也存在较明显的共性：其相关系数均大于0.96，其中月平均降水量的相关系数高达0.995，这说明不同方法计算得到的全国平均降水量具有高度近似的变化特点。分别抽取全国7月、1月和年平均降水量，各有30个样本(1980～2009年)并绘制成图 5，在直观上展示了两种方法得到的平均降水值异同，可以看到7月、1月及年平均中，方法一对应的曲线都在方法二相应曲线的上方；同时，也看到这两两成对的曲线相同点：每组曲线的走势基本相同，也就是说有较高的相关性。形成两种方法有上述异同可能原因分析：根据公式(3)，方法一中对每个数据点的权重系数都是相等的，方法二则认为应根据站点对应面积大小而决定权重，参与计算观测站大多数位于我国东部，但站点稀疏的西部面积大，西部降水量普遍偏少，而在方法二中，西部站点将赋予更大的权重系数，所以方法二得到的全国平均降水量都偏小；方法一和方法二都是使用相同的站点资料进行计算，所以两种方法计算出的全国平均值表现出较高的相关性。

表1(Table 1)

表 1两种方法计算的全国日(月、年)平均降水量比较 Table 1 Comparison of daily，monthly， and annual average precipitation in China between two methods 全国日平均降水量 全国月平均降水量 全国年平均降水量 均值(mm) 标准偏差(mm) 均值(mm) 标准偏差(mm) 均值(mm) 标准偏差(mm) 方法一 2.459 2.310 2.452 1.621 2.449 0.141 方法二 1.719 1.552 1.714 1.218 1.712 0.092

表 1两种方法计算的全国日(月、年)平均降水量比较 Table 1 Comparison of daily，monthly， and annual average precipitation in China between two methods

图 5 两种方法计算的全国平均降水量对比 Fig. 5 Comparison of precipitation averaged over China between the two methods

在分析了平均降水量的两种方法计算结果异同时，只使用了30年的样本，因此，有必要考虑统计特性，进行总体估计，开展假设检验。

方法一和方法二计算出的年平均降水量进行总体均值比较分析，作为前提条件，首先要进行正态性检验和方差奇性检验。当8≤n≤50时(n为样本数)，可以利用Shapiro-Wilk方法，Shapiro-Wilk检验(Shapiro and Willk， 1965)是在对样本次序排列后进行正态性分析，将30个年均降水量值按由小到大循序排列：X₁≤X₂≤…≤X₃₀，若有样本值相等，将重复列出。

检验假设H₀：总体服从正态分布。Shapiro-Wilk检验中的W值计算式如下：

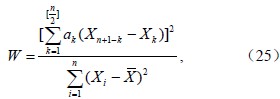
其中，X=(X₁+X₂+…X_n)/n；[n/2]即对n/2取整，当n为偶数时，[n/2]=n/2，n为奇数时，[n/2]=(n－1)/2；
(a₁+a₂+…a_k)=m^TV^-1/(m^TV^-1V^-1m)^1/2，m为标准正态分布次序统计量的数学期望值向量，V是相应的协方差矩阵。

从a_k系数表中查n=30时对应的a_k值，并代入方程，求得方法一的W₁=0.975、方法二相应的W₂=0.973；使用W检验p分位数表，在检验水平a=0.05、样本容量n=30时，查表得到统计量W的a分位数W_0.05=0.927；方法一和方法二对应的W₁、W₂都大于0.927，所以不拒绝原假设，认为两种计算方法求得的年平均降水量总体服从正态分布。

方差奇性检验：检验假设为H₀:σ₁²=σ₂²，H₁:σ₁²≠σ₂²(σ₁²和σ₂²分别为方法1和方法2的总体方差)；检验统计量F=s₁²/s₂²(s₁²和s₂²分别为方法1和方法2的样本方差)，v₁=v₂=29查表F_0.05(29,29)=2.09，F>F_0.05(29,29)=2.09，所以在α=0.05水平上拒绝原假设，认为方法1和方法2求得的全国年平均降水量总体方差非奇性。

两方法求得的全国年平均降水量分别服从正态总体N(μ₁,σ₁²)和N(μ₂,σ₂²)(μ₁和μ₂分别为方法1和方法2的总体均值)，其中μ₁、σ₁²、μ₂、σ₂²均未知，要在一定信度，分析方法1得到的总体均值是否高于方法2。

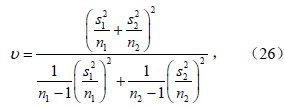
通常将自由度取整[v]，可得[v]=49；查t分布临界值表t_0.05(49)=1.677。

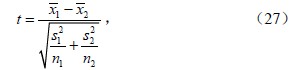
计算得t=24.116>t_0.05(49)=1.677，在α=0.05的水平上拒绝H₀，即认为方法1计算出的年平均降水量总体均数要大于方法2相应值。

某个区域的平均降水量，可以使用不同方法得到数值各异的计算结果，那么就需要有合理的手段分析其结果的客观性。通常是采用有较可靠、高分辨率的数值预报作为分析的依据；欧洲中心数值模式的地面降水预报，由于有较高的准确率，被广泛应用于我国气象预报业务中；若假设欧洲中心的降水预报为“真值”，就可以对不同方法计算下的全国平均降水量的合理性进行一定的分析。

使用2009年的欧洲中心的降水预报产品，选择每天的24 h时效的日降水量预报近似为“真值”；由于数值模式产品是均匀分布的网格点上的预报，对于某日的全国平均降水量，就可以使用简单的算术平均法求出；欧洲中心的地面降水预报分辨率为0.5°(纬度)×0.5°(经度)，位于中国陆地上的格点数是3834，可以分别计算出日、月、年的全国平均降水量。

全国月平均降水量比较中(表 2)：在多数月份，方法二得到的全国月平均降水量和数值模式的降水量预报更接近，夏季(6～8月)是全国降水量最多的季节，方法二得到的平均降水量明显比方法一更接近数值预报；但是，在冬季(1、2、12月)，方法一得到的平均降水值和数值预报更近似。全国年平均降水量比较中(表 2)：方法二计算的结果(1.57 mm)要比方法一(2.25 mm)更接近于数值预报(1.86 mm)。

表2(Table 2)

表 2 数值预报和两种方法计算的2009年全国逐月平均和年平均降水量对比 Table 2 Comparison of monthly and annual average precipitation in China among numerical weather prediction and the two methods in 2009 平均降水量(mm) 欧洲中心数值预报 日本数值预报 方法一 方法二 1月 0.39 0.45 0.33 0.22 2月 0.98 1.08 0.98 0.56 3月 1.27 1.42 1.63 1 4月 1.83 2.06 2.41 1.54 5月 2.3 2.53 3.02 2.11 6月 3.47 3.63 4.23 3.11 7月 3.91 3.82 4.91 3.59 8月 3.44 3.07 4.18 3.08 9月 2.11 1.98 2.35 1.67 10月 1.05 1.05 0.98 0.71 11月 0.91 1 1.4 0.84 12月 0.6 0.67 0.65 0.41 全年 1.86 1.9 2.25 1.57

表 2 数值预报和两种方法计算的2009年全国逐月平均和年平均降水量对比 Table 2 Comparison of monthly and annual average precipitation in China among numerical weather prediction and the two methods in 2009

依据公式(3)，不同方法得到的平均降水值和站点疏密度及降水分布特点有密切关系，所以我国西部稀疏的站点形成两种方法计算结果差异的原因之一。由于我国东部观测站数量上要远多于西 部，故方法一中东部站点降水量整体权重就很大；相反，在方法二中，就单个观测站而言，西部的观测站权重系数要高于东部；因为东部降水量通常大于西部，所以方法一得到的全国平均降水量始终是大于方法二。通过数值模式降水预报得到的平均降水量基本介于方法一和方法二之间，其可能的原因是：我国西部在极为有限的观测站的情况下，就会有不少中小尺度的降水过程无法观测到；但是在 均匀网格分布下的数值预报，却能反映出西部这些降水过程，相当于增加了西部降水量，结果是数值降水预报计算得到的全国平均降水量要高于方法二；也由于数值预报是均匀格点上的预报，相对于方法一，就降低了东部密集站点对应的权重系数，所以其相应的全国平均降水量往往低于方法一。

冬季，全国降水量都偏少，处于“旱季”，例如数值预报对应的2009年1、2、12月的月均值分别是0.39 mm、0.98 mm、0.6 mm(表 2)，我国东部和西部的日降水量在强度上相差并不大，那么西部极为有限的观测对应的缺点就凸显了，因为有很多降水过程无法观测到；另外一个因素是2009年我国发生了较严重的旱灾，北方30年一遇的旱灾(对应1月和2月)，南方50年一遇的秋旱，极端干旱事件频发，这些旱灾大部分发生在站点密集的东部地区；这两方面因素促使数值预报对应的全国月平均降水量高于方法二，接近甚至略大于方法一，这个特点在2009年秋季也有一定程度的表现(表 2)。从上述角度来看，方法一是通过东部站点有较大的权重达到有较高的全国平均降水值；数值预报是通过获得不同尺度的降水量，特别是广大西部区域精细的降水量，从而出现大于方法二的全国平均值；所以，即使数值预报在冬季的全国平均降水值和方法一近似，但产生这种结果的原因是不同的，不能凭此认为方法一就比方法二计算更合理。

夏季，我国各地降水偏多，处于全年的“主汛期”；东部和西部的降水特点有较大的差异：在降水量级、持续时间、影响范围来看，东部地区都要大于西部；虽然数值预报中“增加”了西部更为精细的降水量，但这些降水量数值上是要远小于东部地区的降水，所以，在夏季，更能反映出不同方法的客观、合理性。

日本的数值模式预报格距为1.25°(经度/纬度)，以其每日的24 h预报中的日降水量预报为参考值，共有605个格点位于我国陆地区域，通过算出这605个格点的平均值，可以求得2009年日本数值模式在我国陆地区域上的月、年平均降水量(表 2)；在两个数值模式计算结果比较上：全年平均来看，日本(1.9 mm)和欧洲中心(1.86 mm)的数值模式平均降水量基本接近；在有些月份(7、8、9月)欧洲中心对应的月平均值略大，而其他月份又略小，这种差异可能和数值模式性能和使用的资料有关，两个数值模式的月平均降水量数值总体上相差不大。

由表 2，方法一、方法二和日本数值模式相应的平均降水量比较中，可以得到和欧洲数值预报值相近的分析结果：在降水量较大的月份(例如在全国平均降水量大于3 mm的月份)，方法二算得的月、年平均降水量更为接近日本数值模式，尤其在8月，方法二(3.08 mm)和日本数值模式(3.07 mm)的平均降水量值近似相等。

根据国家气象中心的气候区划，西南地区和西藏分界线是100°E；本文也将100°E以西地区设为我国西部地区，从站点分布来看，在此区域的测站是稀疏的，这样，有利于不同方法的对比分析。在100°E以西的我国大陆地区，欧洲数值模式有1593个格点，日本数值模式格点数为234个，西部测站共有195个。同样以2009年为例，对不同模式和方法进行对比；需要说明的是，表 3是使用西部地区的降水量乘以不同方法中的权重得到的值，从表 3的数值上来看：欧洲和日本的数值模式关于我国西部降水量十分接近，例如全年值分别是0.53 mm、0.45 mm，在降水量较少月份的两者数值上差异较小；在数值上，方法二是方法一的2～3倍，两种方法计算结果有着较大的差别；同方法一比较，方法二的计算值更接近数值模式降水量预报值。

表3(Table 3)

表 3 数值预报和两种方法计算的2009年100°E以西地区月平均和年平均降水量 Table 3 Average precipitation in the region west of 100°E from numerical weather predictions and the two methods in 2009 平均降水量(mm) 欧洲中心数值预报 日本数值预报 方法一 方法二 1月 0.14 0.12 0.01 0.02 2月 0.28 0.25 0.03 0.05 3月 0.27 0.33 0.03 0.06 4月 0.37 0.49 0.07 0.13 5月 0.68 0.74 0.12 0.34 6月 0.86 0.72 0.16 0.41 7月 1.18 0.89 0.2 0.71 8月 1.02 0.69 0.21 0.66 9月 0.72 0.5 0.14 0.36 10月 0.44 0.31 0.05 0.14 11月 0.25 0.23 0.04 0.09 12月 0.16 0.16 0.01 0.03 全年 0.53 0.45 0.09 0.25

表 3 数值预报和两种方法计算的2009年100°E以西地区月平均和年平均降水量 Table 3 Average precipitation in the region west of 100°E from numerical weather predictions and the two methods in 2009

由于表 3是全国平均降水量的西部份额，把表 3和表 2结合分析才更为合理，使用表 3中的数值除以表 2相应的数，并用百分数比较，例如：欧洲中心数值模式2009年计算全国年平均降水量的西部比例是(0.53/1.86)×100%，可得28%。依据上述比较方法，欧洲中心数值模式在夏季(6～8月)相应值是25%、30%、30%，日本数值模式夏季对应值是20%、23%、22%，方法一是4%、4%、5%，方法二是13%、20%、21%，方法二中西部对应的百分比和两个数值模式比较接近，方法一计算出的西部百分比则相差悬殊；2009年全国年平均降水量，欧洲中心数值模式、日本数值模式、方法一、方法二中西部百分值分别是28%、24%、4%、16%，可见，在年平均比较上，方法二和数值模式计算结果相对较接近，方法一有较大差异。所以，在计算全国范围的平均降水量时，方法二更为客观。

虽然本文是从全国范围内分析不同计算方法求得的平均降水量差异，由于不同地区气候差异和观测站点疏密度不同，有必要了解更小的区域中，在不同站点密度分布情况下，对两种方法异同进行比较。由于长江中下游地区是我国降水较强的区域，也是观测站点比较密集的地区；下文将针对长江中下游地区，在不同密度的观测站情况下，分析不同方法计算出的平均降水量差异；长江中下游范围是根据国家气象中心通常使用的气候区域划分方法，其所在的范围为：25°N～35°N，110°E以东地区；此区域有647个观测站，可以设计出4组观测站数据；第一组为全部的观测站，共有观测站数为647个；第二组是从第一组中随机抽取出二分之一的站，得到323个观测站；第三组是从第二组中随机抽取出一半的站，得到161个观测站；第四组同样也在第三组中随机抽出一半的站，共有80个站。根据以上四组观测，可以分析在密度不同的观测站分布对区域平均降水量计算的影响。

表 4展示了长江中下游地区，在4组不同观测密度情况下，两种计算方法得到的2009年平均和月平均降水量；同表 2类似，表 4也列出了欧洲数值模式和日本数值模式的降水量预报，都是使用其24 h的日降水量预报进行分析，其中欧洲数值模式在长江中下游地区有442个格点，日本数值模式有63个格点。首先，在不同密度的观测情况下，区域的月、年平均降水量差异较小，也就是说，观测站点的疏密度对长江中下游的月、年平均降水量影响不大；例如方法一中，从第一组(647个测站)到第四组(80个测站)区域月、年平均降水量变化较小，方法二中也呈现相似的变化特点。其次，方法一和方法二计算得到的长江中下游地区月、年平均降水量比较接近，这和全国平均降水量的比较有着较大的差别。最后，欧洲中心和日本的数值模式来看，和使用实况观测计算出的月、年平均降水量也没有明显的差异；由于第一组有647个观测站，相对于长江中下游地区而言是足够密的，由实况观测算出的平均降水量可近似认为是“真值”，那么在某种程度上也说明数值模式降水量预报的合理性。

表4(Table 4)

表 4 数值预报和两种方法计算的2009年长江中下游地区月平均和年平均降水量 Table 4 Comparision of monthly and annual average precipitation in the middle and lower reaches of the Yangtze River among numerical weather prediction and the two methods in 2009 平均降水量(mm) 欧洲中心 数值预报 日本数 值预报 方法一 方法二 1月 0.53 0.62 0.74 0.74 0.73 0.73 0.75 0.76 0.75 0.75 2月 3.06 3.02 2.52 2.49 2.46 2.52 2.47 2.45 2.46 2.54 3月 3.29 3.16 3.44 3.45 3.43 3.46 3.59 3.61 3.64 3.63 4月 4 3.68 3.9 3.94 3.95 3.99 4.14 4.25 4.26 4.24 5月 4.11 3.7 4.19 4.25 4.24 4.31 4.42 4.51 4.45 4.46 6月 6.04 4.86 5.52 5.55 5.53 5.7 5.71 5.79 5.78 5.91 7月 5.77 5.58 6.07 6.11 6.08 6.31 5.92 5.96 6.02 6.25 8月 4.99 4.65 5.02 5.07 4.98 5.16 4.8 4.76 4.75 4.88 9月 2.31 1.92 2.1 2.18 2.26 2.36 2.05 2.12 2.14 2.15 10月 0.73 0.72 0.6 0.6 0.58 0.61 0.65 0.65 0.61 0.6 11月 2.24 2.78 3.08 3.06 3.05 3.03 3.09 3.06 3.07 3.06 12月 1.26 1.38 1.48 1.49 1.49 1.5 1.5 1.52 1.52 1.53 全年 3.19 3.01 3.22 3.24 3.23 3.31 3.26 3.29 3.29 3.33

表 4 数值预报和两种方法计算的2009年长江中下游地区月平均和年平均降水量 Table 4 Comparision of monthly and annual average precipitation in the middle and lower reaches of the Yangtze River among numerical weather prediction and the two methods in 2009

由表 4中的长江中下游平均降水量呈现出上述变化，其初步分析如下：首先，对于较小的区域，会有相似的气候特点，也就是说，在长江中下游地区的大部分测站观测到的月、年总降水量差异较小；那么，既使在测站分布疏密变化、平均值计算方法不同，在一定条件下，使用两方法计算出的区域月、年平均降水量相差不大。其次，当平均值取的时间越长，两种方法计算结果差异也越小，因为平均降水量还和区域降水量分布特点有关；平均 值取的时间长度越短，降水量空间分布差异性较大，那么对不同的面积加权法影响也就越大，相 反，则越小。

(1)对于较大范围的区域，通常是使用简单的算术平均法计算平均降水量，但是观测站点分布并不均匀分布，根据平均降水量定义，应当考虑站点的疏密度，即站点所代表的局部区域面积大小。我国幅员辽阔、东部和西部气象观测站点分布极不均匀，因此使用Delaunay三角法得到的全国平均降水量较传统的算术平均法更为合理。

(2)全国陆地外边界构成的多边形是一个凹集，因此，需要进行区域的Delaunay三角剖分，本文采用的方法是对外边界收集采样点，然后和观测点构成一个初始点的集合，以此为基础，使用随机增量法剖分，最后生成一个较理想的全国区域的Delaunay三角网。由于有完备的算法支撑，可以随着测站的变化动态生成Delaunay三角网，不受资料时空变化的影响，提高了方法研究和应用价值。

(3)根据球面三角面积公式，将站点位置经纬度表达的大地坐标转换到空间直角坐标系中，应用平面三角余弦定理，求出球面三角的内角，实现了区域Delaunay三角网中每个三角片面积的计算，利用三角片面积大小，可以确定每个观测值的权重系数，最终完成全国平均降水量的计算。

(4)使用全国2200个观测站30年的日降水量资料，两种方法在不同时间尺度(日、月、年)的全国平均降水量的比较中，Delaunay三角法得到的全国平均降水量之均值明显低于算术平均法，表明在较大区域、测站分布不均时，基于传统的算术平均降水量计算方法必须进行适当的修正，以便获得更为合理、精确的数值；同时，两方法计算的平均降水量也有较高的相关性。

(5)对于两方法计算的全国平均年降水量进行了统计检验。通过建立在次序值基础上的Shapiro- Wilk检验，在显著性α=0.05时，认为两方法相应的全国平均年降水量总体服从正态分布；F检验表明其总体方差的非奇性；在显著性α=0.05时，可以认为使用算术平均法计算出的全国年平均降水量之总体均数偏大。

(6)使用欧洲中心和日本2009年数值预报，同两方法对应的全国和长江中下游地区平均降水量进行了比较，分析表明：在夏季，方法二计算结果和数值预报相近，总体上，方法二较方法一更具合理性。不同的方法得到的平均降水量差异大小主要受以下因素影响：取平均的时间长度、降水量分布特点、站点疏密度等；对于较小区域(长江中下游地区)，大部分测站有相似的气候特点，在不同疏密度的站点分布情况下，两方法求得的年(月)平均降水量差异较小；对于大区域(全国范围)，两方法的计算结果有较大差别。

(7)观测站点有较丰富的信息，除了空间位置(经纬度坐标)外，还有降水量的多少、海拔高度、地形特点和区域气候背景等，本文在Delaunay三角剖分时，只考虑了站点空间位置；当要考虑每个点的其他性质时，则将每个点赋予一个“权”，将原来的欧氏距离转换成Power距离，并在此基础上剖分，称之为Regular三角化，这是三角剖分法的研究热点；充分发挥Regular三角法的优势，逐步提高平均降水量计算的精度，是下一步研究的方向。

致谢 中国科学院大气物理研究所的朱江研究员指导了本项研究，对本文提出了许多珍贵的建议和修改意见，在此谨向他表示诚挚的敬意和衷心的感谢。