2 中国科学院大气物理研究所中层大气与全球环境探测重点实验室, 北京 100029
2 Laboratory of Middle Atmosphere and Global Environmental Observation, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
20世纪80年代起时间序列的非线性分析有了长足的发展和进步。1980年,Packard et al. (1980) 提出从实验数据中重构奇异吸引子的思想,这一思想以及后来Takens (1981) 的“嵌入定理”,奠定了从 实际资料入手,研究非线性系统的理论基础。此后,一系列单变量时间序列分析方法和预报方法在此理论基础上发展起来。
然而,被分析的时间序列能否很好地重构动力系统?事实上,描述气候过程的时间序列,其长度是非常有限的,远远少于理论依据所要求的资料数量,这个问题被称为时间序列理论的应用瓶颈,即 “数量瓶颈”(Ellner, 1991; Smith, 1992)。从本质上讲,预测系统未来的状态,预测精度取决于对其历史状态的了解程度,过短的时间序列不可能完整地重构系统的动力系统。
为了解决上述问题,科学家们开展了一些“场时间序列”的试验研究。他们尝试利用空间资料来弥补时间序列长度的不足,以此来重构动力系统,这些研究首先从气候吸引子的维数估计开始,并取得了成功( Tsonis and Elsner, 1988; Yang et al., 1994)。Yang et al.(2000)利用场时间序列思想,通过神经网络建模方法对大气O3浓度垂直总量的月平均值在我国的分布进行了预测试验,结果表明其预测精度达43%以上。另外,根据场时间序列分析的思想,Chen et al.(2003)改进月动力延伸预报,得到了较好的预测精度;Wang et al.(2004)建立“场时间序列”的局域近似预测模型对北半球500 hPa月平均高度场进行预测试验,同样得到了令人鼓舞的结果。应该说,“场时间序列”预测理论可以有效地改善系统的遍历性,在很大程度上提高了气候预测的水平,对进一步弄清空间信息对时空序列的预测精度的影响,改善预测结果有着重要的意义。
另外,在一些天气和气候过程中,人们发现了大气过程的平稳性被改变的事实。例如,Tsonis (1996)通过对近百年的全球降水过程的年际变率的分析,发现降水平均值的涨落有明显地增大(表明旱涝极端事件的频发),说明全球降水资料描述了一个非平稳过程。考虑到,系统非平稳行为的根本原因在于外部强迫随时间的变化(Manuca and Savit,1996),王革丽等(2011)发展了一个建立在外强迫基础上的预测模型,并应用于一些单变量时间序列及气候时间序列上,试验结果表明该方法可以有效的提高预测精度。
因此,本文尝试将外强迫信号的引入及场时间序列分析这两种建模思想结合起来,将外强迫信息和空间信息嵌入到重建的系统之中,建立非平稳场时间序列的区域预测模型,对33模Lorenz系统得到的“理想”非平稳场时间序列进行预测试验分析,检验外强迫信息和空间信息对预报结果的影响。
利用时间序列建立非线性预报模式的研究是在20世纪80年代后半期发展起来的,非线性预报方法大体上分为两类,即状态空间动力学预报模式和神经网络预报模式,它们都是以重构动力系统的理论和方法为基础的。
状态空间动力学预报模式在本质上是利用历史上相似状态的演变来预报当前状态未来的演 变,即建立在寻求动力学相似的基础之上。当恢复了一个给定的时间序列原来系统的动力学以后,我们就拥有一条描述系统状态演变并缠绕在状态空间中的吸引子的轨线,系统状态就按照这个轨线演变发展。因此,需要在当前状态附近找出一个点域,通过结合这些邻近相点的信息,根据猜测或者已有的物理学上的知识构造一个映射,并用它来预测当前点未来的演变。通常根据用以构造映射点集的规模,分为局部近似、全局近似以及介于二者之间的辐射函数基近似3种方法。其中全局近似法是局部近似方法的一种延伸,用以产生映射的点集包含了吸引子上的全部相点,对任何的当前点而言,它只是一种形式,是依次构成的,也就是说,它不需要随着当前点的变更而改变映射的形式或参数。一般情况下,它需要使用更高阶的多项式逼近,因而也就有更高的预报精度。因此,将本文采用了全局近似法对33模Lorenz系统得到的“理想”的非平稳场时间序列进行预测实验分析。
首先,以多项式作为标准函数基,并以外推预报一步为例,来说明单变量时间序列的全局近似法的基本步骤(吕金虎等,2005)。首先假定时间序列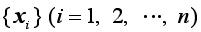 已被嵌入到一个m维的空间中,其轨线记为
已被嵌入到一个m维的空间中,其轨线记为
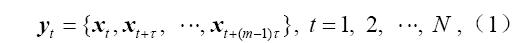
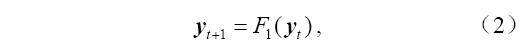
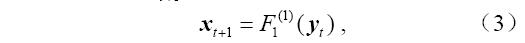
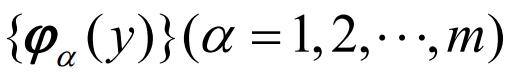 ,然后预报方程的映射F展开成
,然后预报方程的映射F展开成
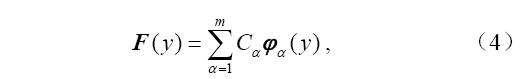
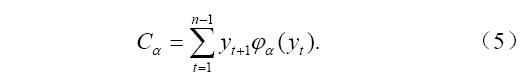
由此,求近似的系数问题转化成一个求经验正交函数展开式的系数问题,后者系数的数目要远小于前者,从而使问题大大简化。
上面概括了单变量时间序列全局近似建立预测方程的一些基本思想及方法。考虑到,外强迫因子随时间的变化是导致动力系统产生非平稳行为的根本原因。鉴于此,王革丽等(2011)给出在建模过程中,外强迫因子直接参与了预测方程的构建,下面简要给出此方法的思路:
考虑包含两个时间序列{xi}(i=1,2···,n)和 {ai}(i=1,2···,n)的一个非线性、非平稳过程,前者是系统的状态随时间的变化,而后者表示其外强迫随时间的演变。借助于一个适当的时滞参数t,可以将它们嵌入到m1+m2维的状态空间中,并得到如下的状态轨线:
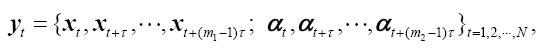
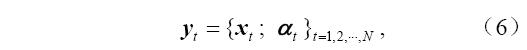
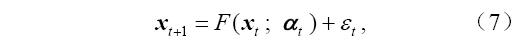
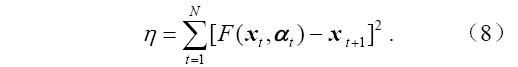
另一方面,作为单变量时间序列的推广,场时间序列的基本思想是,对空间区域的某一个点,重构其状态空间,恢复原来系统的动力学,如果空间区域上的所有点都是处在同一个动力学系统控制之下,那么经过状态空间重构后,这些描写系统动力学的轨线段都将缠绕在同一个吸引子上。也就是说,对于空间区域内的某一个点,它的动力信息不仅保留在它自身的发展序列中,而且还应保留在整个区域内的其他空间点中。
因此,在上述两种方法的思想下,不仅将外强迫因子引入到重建的系统中,同时利用场时间序列思想,将预测相点空间区域四周相点的信息也引入到系统中,仿照公式(7),其预测方程可以写为
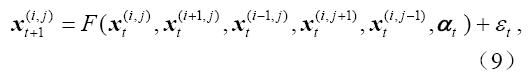
在此意义下的状态轨线,参照单点时间序列,通过寻找映射关系来建立预测模型,也就是说,要综合考虑空间区域其他点的信息,用空间资料来弥补时间资料的不足;另一方面,在预测模型中,引入外强迫因子,让外强迫因子与状态变量在预测中扮演同等重要的角色。下面通过两个预测试验来检验该预测技术的效果。
为了叙述方便,在下面的预测试验中,把不包含外强迫因子的预测模型称为平稳性模式,包含外强迫因子变化的预测模型称为外强迫模式,包含外强迫因子变化和四周空间信息的预测模型称为空间外强迫模式。
由于观测上或技术上的某些原因,大多数来自实际的时空序列,都不可避免地受到噪声的污染及时间序列数量的限制。因此,通常会从一些“理想”的实验资料上进行分析。
1963 年,Lorenz(1963)在研究长期天气的可预报性问题时,发现了著名的Lorenz系统,即把二维Benard对流问题变成了一个只包含3个谱模分 量的方程组,Curry(1978)和杨培才(1987)又分别将谱模增加到14和33个,并充分证明了模态的增加将引起解在参数空间中分布的重大变化。基于上面的这些工作,选择33模Lorenz系统作为二维Benard对流的截谱方程,并用它给出的对流系统的流场随时间变化作为“理想”非平稳场时间序列(杨培才,1987;王革丽等,2006)。对于得到的时空序列,它们满足以下条件:1)场时间序列几乎没有无污染;2)在积分过程中,改变Rayleigh的值,使其随时间变化,这样得到的时间序列是非平稳的;3)改变参数,可以得到不同空间分辨率所对应的流场分布。
对于由33模Lorenz系统所得到的时空序列,将采用前面介绍的平稳性模式,外强迫模式和空间外强迫模式分别进行预测检验。为了检验各个模式的预报能力,给出两个非平稳时间序列的区域预测的试验例子。
利用Hamming算法求解33模Lorenz系统,积分步长取h=0.001,积分110000 步,剔除前 100000步积分的过渡期,这样可以得到33个谱模分量,把33个谱模分量带入对流方程可以得到不同时刻的流场和扰动温度场。取时空参数k=5,用一个5×5的格点网格来刻画流场的空间结构,这样就得到了我们所需的时空序列。图 1为Rayleigh数r=1000sin(10t)+1001时33 维Lorenz系统的状态轨迹在(φ11,θ11)相平面上投影,在这里 Rayleigh 数在1~2001变化,相应地,系统的状态在定常解、周期解、准周期解和混沌解之间非周期地变化着,在这样条件下,系统具有非平稳性质。
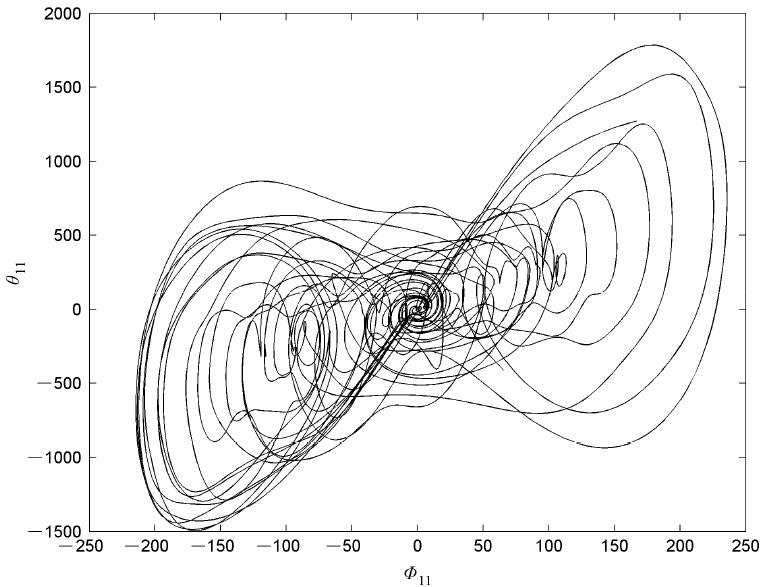 |
图 1 r=1000sin(10t)+1001时33模Lorenz系统的状态轨道在(Φ11,θ11)相平面上的投影 Fig.1 Projection for the state trajectories of 33 mode Lorenz system in(Φ11,θ11)when r=1000sin(10t)+1001 |
下面利用平稳性模式,外强迫模式和空间外强迫模式对上述分辨率为5×5的时空序列进行预测分析,依次预测25个点,用每个点所对应的时间序列的前9500个数据构造映射,后500个数据用于检验预测效果。待预测的时间序列的嵌入维数为m1,本文选择对系统相空间结构研究广泛的Lorenz系统,这些系统的混沌吸引子的维数有很多的研究工作,在此工作基础上进行试探分析,取m1值取为2~6;外强迫因子和空间信息所对应的时间序列的嵌入维数为m2,m2 = 0时表示预测方程中不考虑外强迫因子和空间信息,即采用平稳性模式,而在外强迫模式及空间外强迫模式中m2均取为1。预测的时间序列的延滞时间为τ,根据自相关函数法,求得τ值为1。另外,外强迫模式和空间外强迫模式中外强迫信息为Rayleigh随时间变化的序列,空间信息为预测点四周的时间序列,且所模拟的区域的边界点的四周相点只用到外强迫信息。
从图 2可以看出,利用平稳性模式预测的流场图与真实场有一定的差异,外强迫模式预测的流场图与真实场相差甚微,空间外强迫模式预测出的流场图与真实场几乎重合。
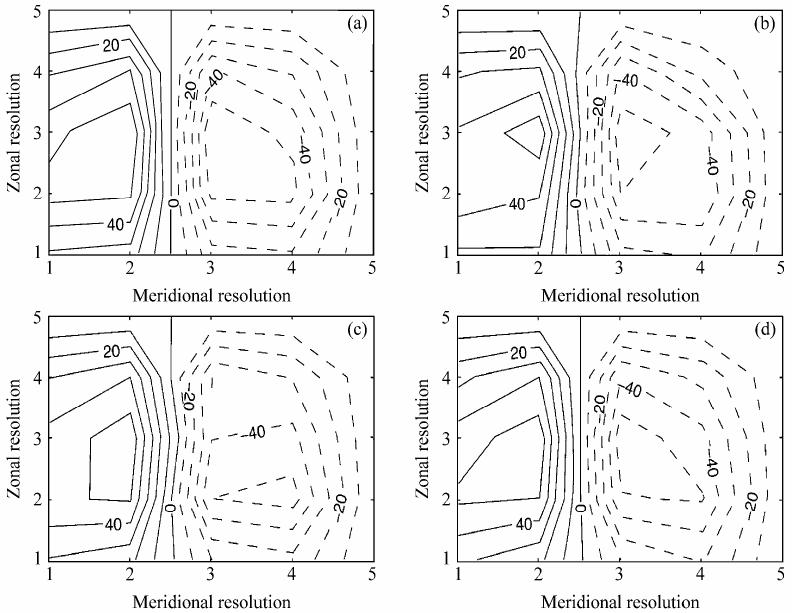 |
图 2 预报步数为6时,(a)实际流场与(b)平稳性模式、(c)外强迫模式、(d)空间外强迫模式预报场的对比(实线和虚线分别表示正值和负 值) Fig.2 The comparison of(a)live field and forecast fields of(b)stationary mode,(c)external forcing mode,and(d)space external forcing mode for the sixth prediction step(solid lines and dashed lines denote positive and negative values,respectively) |
图 3给出了流场的平均相关系数随预报步数的变化情况,可以看出3种预报模式的预测效果都是很好的,在第6步之前3种预报模式与实况的相关系都可以达到0.98以上,但在随后的预报中,随着预报步数的增加,相关系数逐渐降低。当预报步数为10时,空间外强迫模式的相关系数仍可达0.96以上,外强迫模式的相关系数降到0.95,而平稳性模式此时的相关系数已降到0.94。这表明,对于非平稳时间序列的预测,空间信息和外强迫信息的嵌入可以有效修补原来的动力系统,改善系统的可预报性。
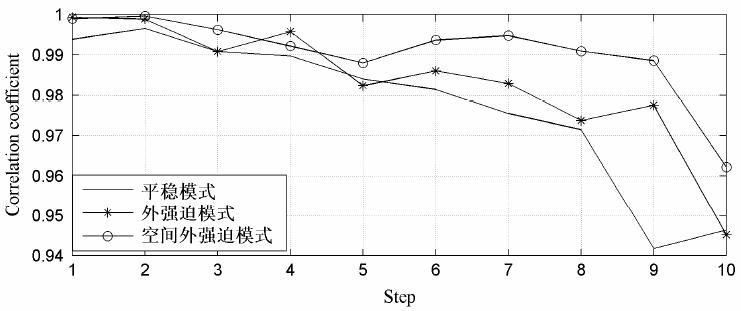 |
图 3 r=1000sin(10t)+1001时平稳性模式、外强迫模式、空间外强迫模式平均相关系数比较 Fig.3 The comparison of the predicted average correlation coefficients from forecast fields of stationary mode,external forcing mode,and space external forcing mode when r=1000sin(10t)+1001 |
另外,由平稳性模式、外强迫模式、空间外强迫模式得到的平均1~10步的均方根误差列在表 1中,空间外强迫模式和外强迫模式的均方根误差分别为1.75%和2.26%,而平稳性模式的均方根误差为2.49%。这表明当考虑外强迫因子及周围相点信息,并将它们引入预测模型时,预测精度可以有所提高。
| 表 1 r=1000sin(10t)+1001时平稳性模式、外强迫模式、空间外强迫模式1~10步预报平均均方根误差的比较 Table 1 The predicted average root-mean-square errors within 1–10 step from forecast fields of stationary mode, external forcing mode, and space external forcing mode when r=1000sin(10t)+1001 |
同样利用Hamming 算法求解33模Lorenz 系统,改变时空参数k为7,得到一个空间分辨率为7×7的格点网格来刻画流场的空间结构。图 4为Rayleigh数r=20t+9时,33模Lorenz系统的(φ11,θ11)分量在相平面上投影,在这里r在29~2209变化,即系统的状态在定常解、周期解、准周期解和混沌解之间非周期地变化着,在这样的情况下,系统处于非平稳状态。
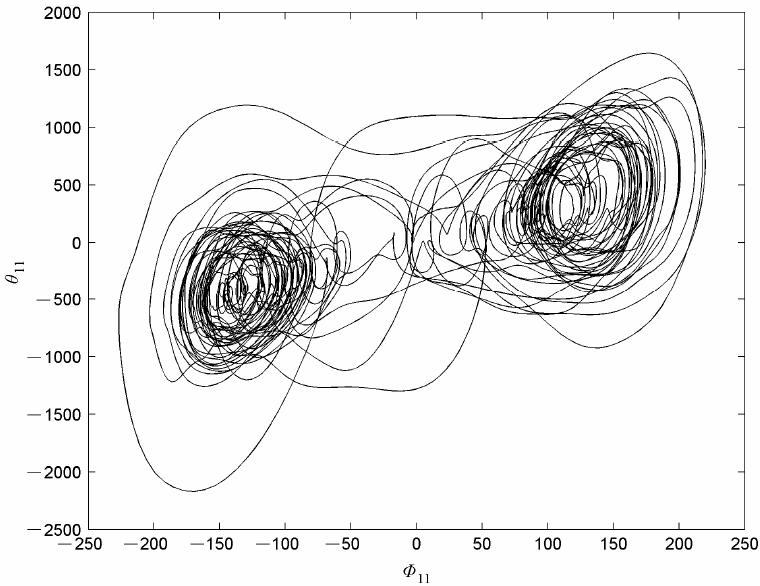 |
图 4 r=20t+9时33模Lorenz系统的状态轨道在(Φ11,θ11)相平面上的投影 Fig.4 Projection for the state trajectories of 33 mode Lorenz system in(Φ11,θ11)when r=20t+9 |
利用平稳性模式、外强迫模式和空间外强迫模式对上述得到的7×7时空序列进行预测分析,试验参数及重构参数皆取与上面的试验相同的值。从图 5可以看出,空间外强迫模式预测出的流场图与真实场几乎重合,利用外强迫模式和平稳性模式预测的流场图与真实场总的分布还是较一致,但仍有一些差异。
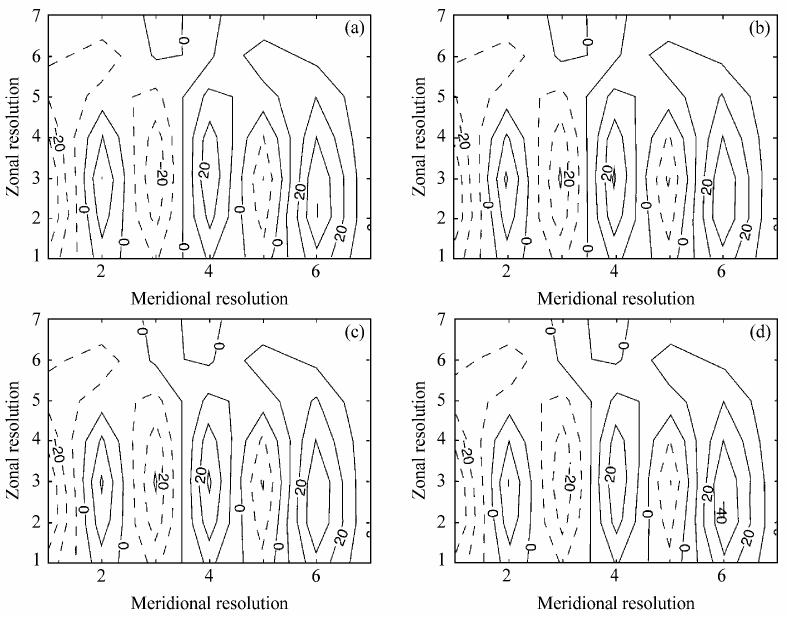 |
图 5 同图 2,但预报步数为7 Fig.5 Same as Fig.2,but for the seventh prediction step |
从图 6可以看出平稳性模式、外强迫模式、空间外强迫模式在第5步之前与实况的相关系数较好。另外,随着预报步数的增加,空间外强迫模式与实况的相关系数减少速度要低于外强迫模式,外强迫模式与实况的相关系数减少速度要远低于平稳性模式。
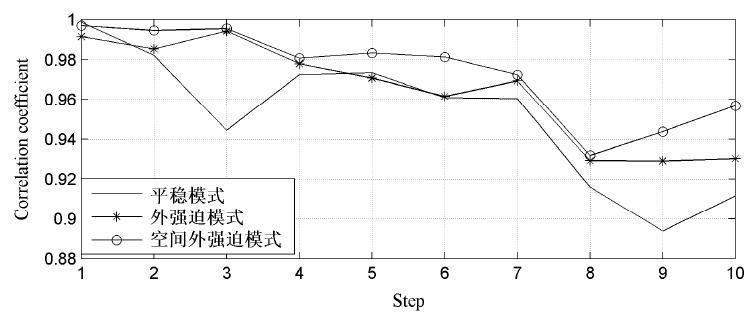 |
图 6 r=20t+9时平稳性模式、外强迫模式、空间外强迫模式平均相关系数比较 Fig.6 The comparison of the predicted average correlation coefficients from forecast fields of stationary mode,external forcing mode,and space external forcing mode when r=20t+9 |
为了便于比较,平稳性模式、外强迫模式、空间外强迫模式得到的平均1~10步的均方根误差列在表 2中。在这组预测试验中,由平稳性模式得到的均方根误差为6.67%,通过外强迫模式及空间外强迫模式得到的均方根误差降低为5.59%及4.53%。
| 表 2 r=20t+9时平稳性模式、外强迫模式、空间外强迫模式1~10步预报平均均方根误差的比较 Table 2 The predicted average root-mean-square errors within 1-10 steps from forecast fields of stationary mode, external forcing mode, and space external forcing mode when r=20t+9 |
综合上述结果,可以得到如下两个结果:1)外强迫模式与实况的相关系数要高于平稳性模式,这说明外强迫信息的嵌入可以有效地改善预测结果;2)空间外强迫与实况的相关系数要比外强迫模式高,这表明同时引入空间和外强迫信息可以进一步提高预测精度。
本文尝试将外强迫信号的引入及场时间序列分析这两种建模思想结合起来,建立非平稳场时间序列的区域预测模型,综合考虑空间区域其他点的信息,用空间资料来弥补时间资料的不足;另一方面,在预测模型中引入外强迫因子,让外强迫因子与状态变量在预测中扮演同等重要的角色。
作为一个初步尝试,本文从“理想”非平稳场时间序列入手,将外强迫信息和空间信息嵌入到重建的系统之中,通过平稳性模式、外强迫模式和空间外强迫模式3种方法,对33模Lorenz 系统得到的“理想”场时间序列发生器建立预测模型,进行预测试验研究。结果表明,外强迫模式和空间外强迫模式对非平稳场时间序列都有较好的预报能 力,且空间外强迫模式能够进一步提高预测技巧,一方面我们可以理解为嵌入外强迫因子是对重构动力系统的某种修补,即更好地重构出原来的动力系统,另一方面在重建的动力系统中引入空间信息,利用空间数据来弥补时间序列长度的不足。
诚然,上述结果是基于理想的场时间序列得到的。对于实际气候资料而言,由于资料的数量以及噪音等因素的存在,其预测效果可能会在一定程度上受到限制,这是我们以后需要关注的科学问题。为了进一步完善非平稳时间序列的区域预测,还需要考虑以下几个问题:1)怎么样去选取外强迫信息,是依据气候因子之间的关联性来确定他们之间的关系,还是直接从时间信号中去提取外强迫信息;2)针对外强迫信息和空间信息的嵌入维数增加的问题,可能对观测数据和质量提出新的要求。因此发展合适的场时间序列建模技术需要我们进一步的探讨和研究。
| [1] | Chen B M, Ji L R, Yang P C, et al. 2003. An approach to improving the dynamical extended-range (monthly) prediction [J]. Chinese Science Bulletin, 48 (7): 696-703. |
| [2] | Curry J H. 1978. Order and disorder in two and there dimensional Benard convection [J]. J. Fluid Mech. , 147:1-38. |
| [3] | Ellner S. 1991. Detecting Low-dimensional Chaos in Population Dynamics Data: A Critical Review [M]// Does Chaos Exist in Ecological System? Charlotteville: University Press of Virginia, 65-92. |
| [4] | Lorenz E N. 1963. Deterministic nonperiodic flow [J]. J. Atmos. Sci. , 20: 130-141. |
| [5] | 吕金虎, 陆君安, 陈士华. 2005. 混沌时间序列分析及其应用 [M]. 武汉: 武汉大学出版, 57-66. Lü Jinhu, Lu Jun'an, Chen Shihua. 2005. Analysis and Application of Chaotic Time Series (in Chinese) [M]. Wuhan: Wuhan University Press, 57-66. |
| [6] | Manuca R, Savit R. 1996. Stationarity and nonstationarity in time series analysis [J]. Physica D, 99 (2-3): 134-161. |
| [7] | Packard N H, Crutchfield J P, Farmer J, et al. 1980. Geometry from a time series [J]. Physical Review Letters, 45 (9): 712-715. |
| [8] | Smith L A. 1992. Estimating dimension in noisy chaotic time series [J]. Journal of the Royal Statistical Society: Series B, 54 (2): 329-351. |
| [9] | Takens F. 1981. Detecting strange attractors in turbulence [M]// Warwick 1980. Dynamical Systems and Turbulence. Berlin, Heidelberg: Springer-Verlag, 366-381. |
| [10] | Tsonis A A. 1996. Widespread increases in low-frequency variability of precipitation over the past century [J]. Nature, 382 (6593): 700-702. |
| [11] | Tsonis A A, Elsner J B. 1988. The weather attractor over very short time scales [J]. Nature, 333 (6173): 545-547. |
| [12] | Wang G L, Yang Peicai, Lü Daren. 2004. On spatiotemporal series analysis and its application to predict the regional short term climate process [J]. Advances in Atmospheric Sciences, 21 (2): 296-299. |
| [13] | 王革丽, 杨培才, 吕达仁. 2006. 33模Lorenz系统的混沌特征及其可预报性分析 [J]. 高原气象, 25 (1): 9-15. Wang Geli, Yang Peicai, Lü Daren. 2006. Chaotic characters and predictability of 33 mode Lorenz system [J]. Plateau Meteorology (in Chinese), 25 (1): 9-15. |
| [14] | 王革丽, 杨培才, 卞建春, 等. 2011. 一个包含外强迫因子的非平稳时间序列的预测方法 [J]. 科学通报, 56(25): 2107-2110. Wang Geli, Yang Peicai, Bian Jianchun, et al. 2011. Forecasting methods with An external forcing factor of non-stationary time [J]. Chinese Science Bulletin (in Chinese), 56 (25): 2107-2110. |
| [15] | 杨培才. 1987. 33模Lorenz系统的某些总体特征 [J]. 大气科学, 11 (1): 48-57. Yang Peicai. 1987. Some gross features of 33-mode Lorenz system [J]. Scientia Atmospherica Sinica (in Chinese), 11 (1): 48-57. |
| [16] | Yang P C, Brasseur G P, Gille J C, et al. 1994. Dimensionalities of ozone attractors and their global distribution [J]. Physica D, 76 (4): 331-343. |
| [17] | Yang P C, Zhou X J, Bian J C. 2000. A nonlinear regional prediction experiment on a short-range climatic process of the atmospheric ozone [J]. J. Geophys. Res. , 105 (D10): 12253-12258. |
 2014, Vol. 19
2014, Vol. 19

