气候与环境研究  2014, Vol. 19 Issue (3): 362-370   PDF    
引用本文
吴晓.2014.从FY-4静止气象卫星估算晴空地表下行长波辐射通量的反演模式[J].气候与环境研究,19(3):362-370,doi:10.3878/j.issn.1006-9585.2013.13032.  
WU Xiao. 2014. Retrieval Model for Estimating Clear-Sky Downward Longwave Radiation at the Surface from the FY-4 Geostationary Satellite[J].Climatic and Environmental Research(in Chinese),19(3): 362-370,doi:10.3878/j.issn.1006-9585.2013.13032.  
从FY-4静止气象卫星估算晴空地表下行长波辐射通量的反演模式
吴晓1,2    
1. 中国气象局中国遥感卫星辐射测量和定标重点开放实验室, 北京100081;
2. 国家卫星气象中心, 北京100081
收稿日期: 2013-2-18 收到, 2013-7-8 收到修定稿.
资助项目： 国家卫星气象中心风云四号静止气象卫星地面应用系统工程-产品算法开发项目
作者简介：吴晓，女，1964年出生，高级工程师，主要从事气象卫星遥感反演。E-mail：wuxiao@cma.gov.cn
摘要：通过红外辐射传输模拟，计算了446183条全球晴空大气廓线的地表下行长波辐射通量以及FY-4成像仪通道亮温，应用统计回归分析模拟结果，建立了通道亮温与低层大气有效辐射温度的回归关系、大气柱总可降水量与低层大气比辐射率的回归关系，依据黑体辐射定律建立了由卫星观测估算地表下行长波辐射通量的反演模式。初步地，模式应用于FY-4成像仪代理资料Meteosat-8卫星的SEVIRI（Spring Enhanced Visible and Infared Imager）仪器观测数据，估算了2006年8月1日00：00（协调世界时，下同）、06：00、12：00、18：00地理范围在（45°S～45°N，45°W～45°E）的地表下行长波辐射通量，结果与用ECMWF 6 h预报场资料经验计算的通量相比，系统均方根误差（RMS）依次为12.1、13.0、20.7、12.5 W/m2，相关系数分别为0.9256、0.9291、0.9042、0.9325，相比于GOES-R同类产品（RMS=13.7 W/m2），这一直接把卫星通道亮温与低层大气温度相联系的反演模式，其精度性能达到了应用研究对其反演产品的质量要求。
关键词： 地表下行长波辐射     辐射传输     统计回归    
Retrieval Model for Estimating Clear-Sky Downward Longwave Radiation at the Surface from the FY-4 Geostationary Satellite
WU Xiao1,2    
1. Key Laboratory of Radiometeric Calibration and Validation for Environmental Satellites, China Meteorological Administration, Beijing 100081;
2. National Satellite Meteorological Center, China Meteorological Administration, Beijing 100081
Abstract: Based on the infrared radiative transfer calculations for 446183 atmospheric profiles, the downward longwave radiation flux at surface and channel brightness temperatures for the FY-4 Imager were simulated. From a regression analysis of the simulated data, a retrieval model relating the flux with channel temperatures and atmospheric precipitable water was established. The model was then applied to Meteosat-8 SEVIRI (Spring Enhanced Visible and Infared Imager) data, adopted as a proxy of the FY-4 Imager, and the downward longwave flux was estimated over an area of (45°S-45°N, 45°W-45°E), at 0000 UTC, 0600 UTC, 1200 UTC, and 1800 UTC Aug 1 2006. The fluxes were then compared with those calculated using empirical equations on ECMWF data. The RMS errors were 12.1, 13.0, 20.7, 12.5 W/m2, respectively. Compared with the RMS 13.7 W/m2 value from GOES-R, the estimates from the model developed in this study would satisfy future climate research requirements.
Key words: Downward longwave radiation     Radiative transfer     Statistical regression    

1 前言

预计于2016年发射的风云四(FY-4)号静止气象卫星，是我国第2代地球同步轨道卫星，星上将载有垂直探测仪和扫描成像仪，完成对地的三维和二维气象观测，成像仪(IMAGER)有14个探测通道，包括6个短波和8个红外通道，除了提供图像产品外，还将处理出30多个气象参数产品，晴空地表下行长波辐射通量是其中之一。地表下行长波辐射(又称大气逆辐射)是指大气向下发射的到达地表的长波辐射通量密度(Downward Longwave Radiation，DLR)，是地表能量收支的参量，对于陆面模式、区域气候模式、大气环流模式具有重要意义。

从气象卫星反演地表下行长波辐射通量源于上世纪80年代，那时科学家利用NOAA卫星TOVS(TIROS Operational Vertical Sounder)仪器的垂直温湿廓线产品通过辐射传输方程计算下行通量(Darnell et al., 1983)，这一方法即为如今的物理反演方法，如Wang W H and Liang(2009)研究的Terra和Aqua卫星MODIS(MODerate-resolution Imaging Spectroradiometer)仪器的DLR产品，但该方法由于计算耗费机时而不被业务产品处理所采用；后来发展的统计反演模式(Ellingson，1995；Lee and Ellingson， 2002；Tang and Li， 2008；Wang W H and Liang(2009))有两类，一类是直接建立卫星通道辐射率与下行通量的统计回归关系，但这一反演模式的产品精度较差，RMS在16～25 W/m2(Wang W H and Liang(2009)；Tang and Li， 2008)，二类是建立卫星通道观测与某些气象参数如近地层气温、水汽含量的统计经验关系，再由地表下行通量的气象经验公式(Wang K C and Liang， 2009)计算通量，目前美国GOES-R的业务产品算法基本上是在后者基础上发展起来的，其产品精度RMS达到14 W/m2。参考了GOES-R的经验，在FY-4产品研制阶段，我们建立了针对FY-4 IMAGER通道的DLR反演模式，这篇文章即是关于这一反演模式建立过程以及初步应用结果的介绍。

2 反演模式提出的理论依据

根据黑体辐射定律，任何温度为T的物体发射的辐射通量密度F可写为

其中，ε是物体的比辐射率，σ是斯蒂芬—玻尔兹曼常数，T是物体的绝对温度。地球大气的辐射是灰体辐射，其比辐射率由大气中吸收气体含量决定，由于到达地面的大气逆辐射99%来源于地面至700 hPa以内的近地层(Darnell et al., 1983)，因此DLR可以近似地写为

其中，FDLR是地表下行长波辐射通量密度即DLR，εa是低层大气比辐射率，Te是低层大气有效辐射温度。因此如果能由卫星通道观测反演得到εa和Te，就可由(2)式计算出DLR，建立反演模式的任务就是建立通道观测与εa、Te的关系。

3 回归模式的建立

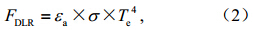
反演模式的建立主要是通过大气廓线的通量模拟、卫星通道亮温模拟、廓线大气柱总可降水量模拟，用统计回归的方法建立通量与亮温、总水汽含量之间的关系。

3.1 红外辐射传输方程及通量模拟

由2010年全年ECMWF(欧洲中心中尺度天气预报)资料整理出的共446183条全球晴空大气廓线用于红外辐射传输模拟，通过辐射传输方程模拟计算逐条廓线的下行辐射率，再由统计经验公式计算逐条廓线的下行通量。

忽略大气散射，到达地表的大气向下长波辐射率由如下辐射传输方程(Lee and Ellingson.，2002)计算：

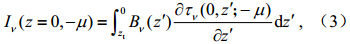
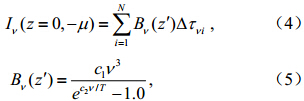
其中，Iv(z=0,-μ)是地表大气向下长波辐射率，v是波数，μ=cosθ，θ是当地天顶角，z是高度，z'是某层大气的高度，zτ是大气顶高度，τv(0,z';-μ)是从z'高度到地表的透过率，关于透过率的详细计算见参考文献(吴晓，1998)，Bv(z')是z'高度上的普朗克函数，(3)式写成级数型式有

其中，Δτv1=τi+1-τi，N=101，文中廓线从大气顶到地表分为101层，c1=1.191066×10-5、c2=1.43833为普朗克常数，如图 1是用2010年7月4日位于(31.00°S，136.25°E)大气廓线计算得到的到达地表的下行辐射率。

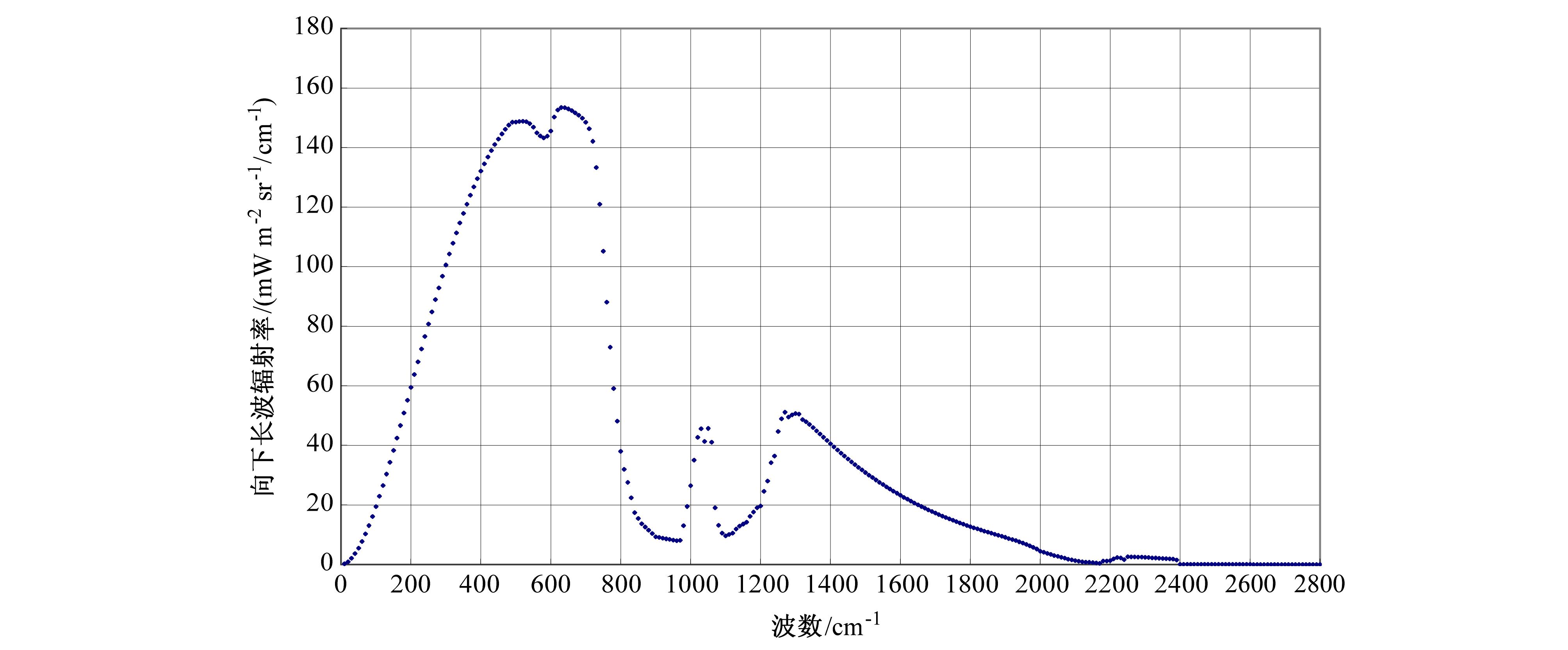图 1 用2010年7月4日(31.00°S，136.25°E)的大气廓线计算的到达地表的向下长波辐射率Fig. 1 The computed downward specific spectral intensities at for atmospheric profile located at(31.00°S，136.25°E)

地表大气逆辐射通量是总波段下行辐射率在下半球立体角的积分，计算公式如下：

4 46183条廓线的总波段下行辐射率I(z=0,-μ)与天顶角θ有如下经验关系(Wark et al., 1962)：

其中，I(z=0,-1)是天顶角θ=0°的总波段下行辐射率。

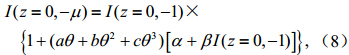
将(8)代入(6)得

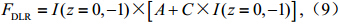
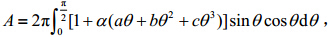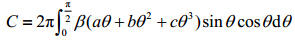其中，，，α、β、a、b、c是446183条廓线的统计回归系数，通过(9)式可以模拟计算出地表下行通量DLR。

3.2 FY-4 IMAGER通道亮温模拟

4 46183条廓线的FY-4 IMAGER通道亮温由如下方程模拟计算得到：

其中，Iv0(z=zt,μ)是通道辐射率，Iv(z=zt,μ)是大气顶射出辐射率，zt是大气顶高度，f(V)是通道光谱响应，v0是通道中心波数，通道亮温TB由普朗克公式的反函数计算：

大气顶射出辐射率Iv(z=zt,μ)由以下辐射传输方程计算(Matricardi and Saunders， 1999)：

其中，εvτ是地表光谱比辐射率，Bv(Ts)是地表温度为Ts的普朗克函数，c1、c2是辐射常数，v是波数，τv是单色透过率，式(12)写为级数型式有

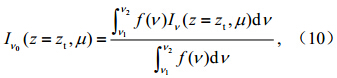
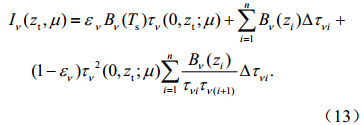
用红外辐射传输方程式(13)编制软件就计算出廓线大气顶射出辐射率，图 2是用2010年4月15日位于(27.25°N、156.25°E)的大气廓线计算出的大气顶射出辐射率。在本文反演模式的建立过程中，通道亮温的模拟最终采用了美国Wisconsin大学开发的RTM软件。

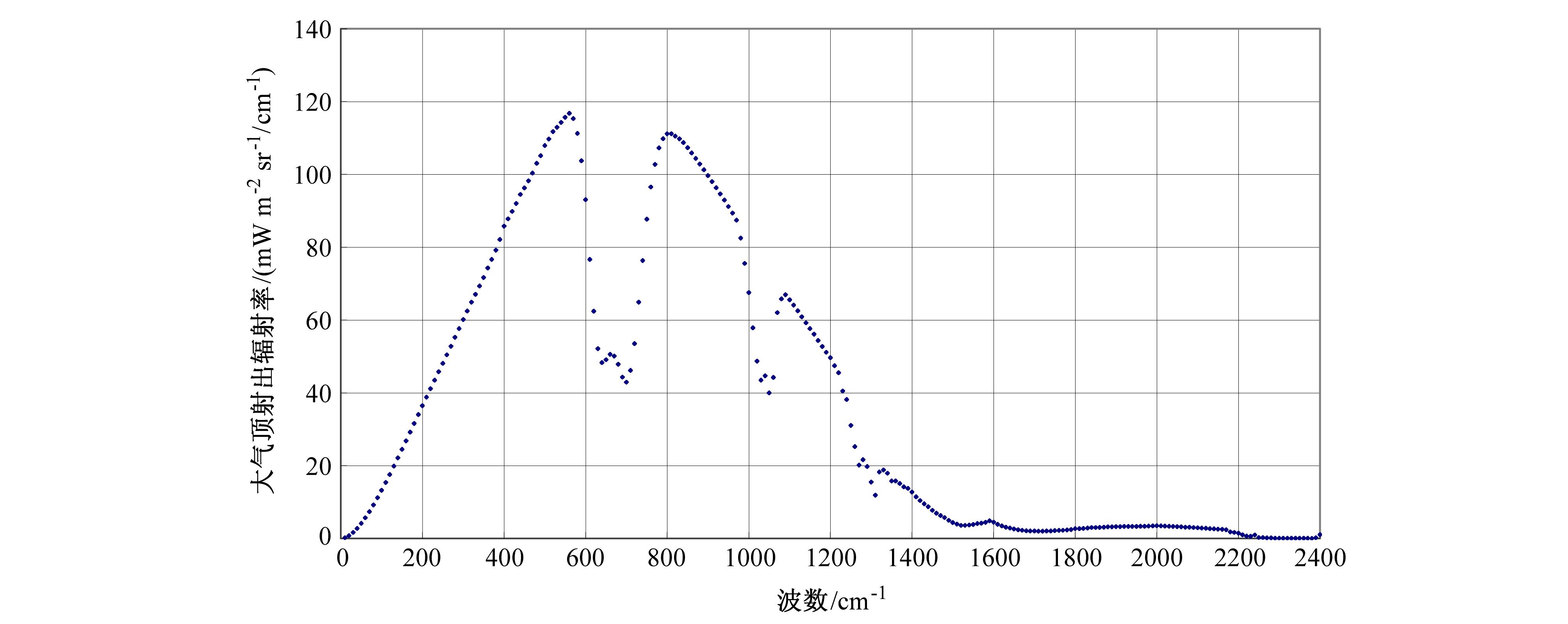图 2 2010年4月15日(27.25°N，156.25°E)廓线大气顶射出辐射率Fig. 2 The computed outgoing spectral intensities at the top of atmosphere(TOA)for atmospheric profile located at(27.25°N，156.25°E)

3.3 建立通道亮温与大气低层有效辐射温度的回归关系

FY-4 IMAGER有14个通道，其光学特性如表 1，与近地层温度相关的有通道12、13、14，这里我们定义低层大气有效辐射温度：

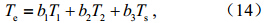
表 1 FY-4 IMAGER通道光谱特性 Table 1 The spectrums of FY-4 IMAGER

其中，T1是地面(若地面气压为1013 hPa)至850 hPa空气层的平均温度，T2是850～700 hPa空气层的平均温度，地表温度Ts可由通道12亮温TB12代替(即Ts=TB12)，T1=(T931+T852)/2，T2=(T777+T706)/2，T931、T852、T777、T706分别是931、852、777、706 hPa层(当地面气压不为1013 hPa时取与地面气压差为75、150、225、300 hPa的层次)空气温度，权重函数b1、b2、b3分别取为0.5、0.3、0.2。由于通道14敏感900～700 hPa的温度，因此可以通过统计的方法寻求通道14亮温与近地层各层温度的关系，图 3是地面气压为904 hPa组廓线上空4个气压层的空气温度与FY-4 IMAGER通道14亮温的回归关系(这里说明一点，由于不同地表高度上气体压力加宽作用对辐射的影响不同，即相同温湿、气体含量等条件下不同高度上大气逆辐射不同，因此将446183条廓线按地面气压ps=1013、958、904、852、802、753、706、661、617、575、535 hPa分为11组分别处理，分别建立各组廓线的统计回归关系，DLR反演时则按不同地面气压查找不同的回归系数)，图 3A、3B中空气温度与通道亮温的回归关系在240 K处分为2段不同线性关系。

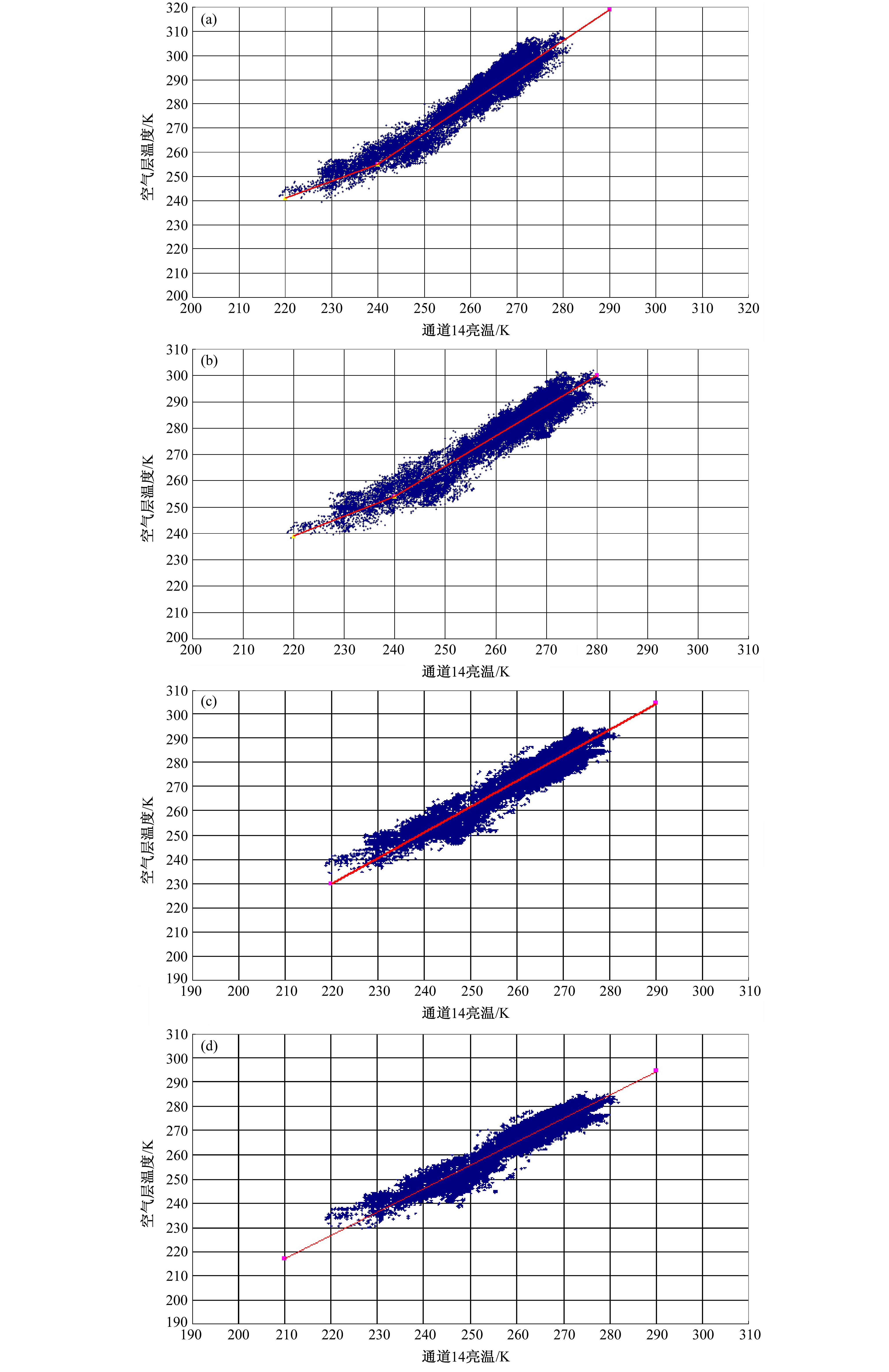图 3 通道14亮温与距地面气压差为(a)75、(b)150、(c)225、(d)300 hPa的空气层温度的关系Fig. 3 The scatter plots between brightness temperature of channel 14 and the air temperature at the level of(a)75-hPa，(b)150-hPa，(c)225-hPa， and (d)300-hPa pressure differences above the surface

由图 3得出低层大气空气温度与通道14亮温的经验关系如下：

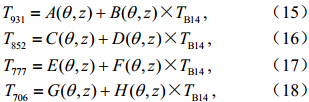
其中，A、B、C、D、E、F、G、H是回归系数，随卫星天顶角θ及地表气压(即海拔高度)而变。

3.4 建立大气柱总可降水量与低层大气比辐射率的回归关系

低层大气比辐射率可由下式求出：

由于在低层大气中，辐射气体CO2、O3相对于H2O含量较为稳定，水汽则随天气气候、地理位置变化，而水汽是0～2500 cm−1光－谱区红外辐射的主要贡献者，因此我们寻求低层大气比辐射率与水汽含量的变化关系，如图 4，从图 4得出εa与大气柱总可降水量w有如下关系：

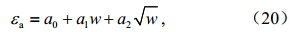
其中，a0、a1、a2是回归系数，随地表高度而不同。从图 4上看出随着总水汽含量w的增大εa出现大于1的现象，这是由于w越大到达地面的DLR来自 于大气更低的层次，文中模拟的与地面气压差300 hPa层内平均有效温度Te小于实际气层的有效辐射温度引起。

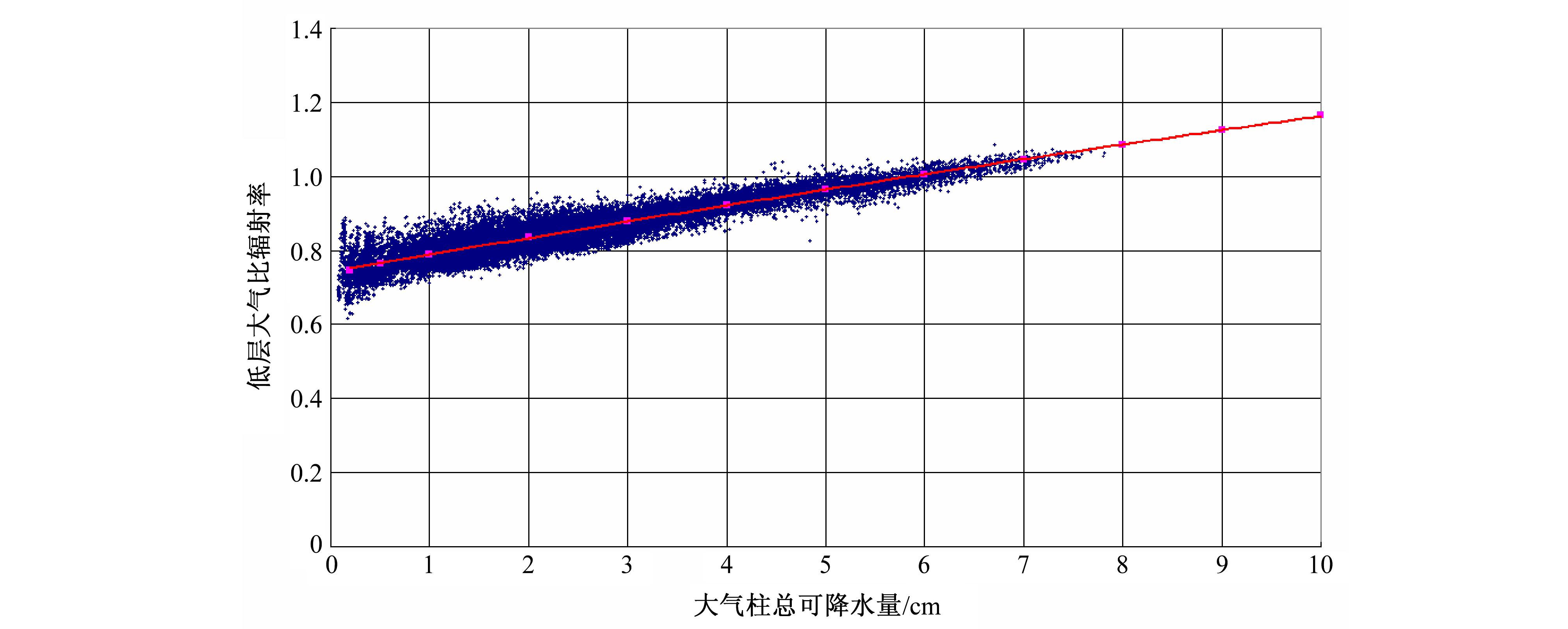图 4 地面气压1013 hPa组廓线低层大气比辐射率与总可降水量的经验关系Fig. 4 The regression plot of precipitable water and lower atmosphere emissivity at 1013 hPa

3.5 模式精度估计

总结以上过程，FY-4 IMAGER的DLR反演模式为

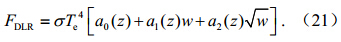
由于式中回归系数随地表气压而异，在实际产品处理时，将卫星观测像点的海拔高度按5个US标准大气廓线转换为对应的地面气压，根据地面气压查找对应的回归系数，w则由FY-4 IMAGER晴空大气可降水量产品(由FY-4 IMAGER通道9、10、11反演得到)提供。

图 5是模式(21)估算DLR与廓线模拟DLR的差值图，对于这组地面气压为1013 hPa的廓线，模式的RMS=8.3W/m2，相关系数R=0.9890。

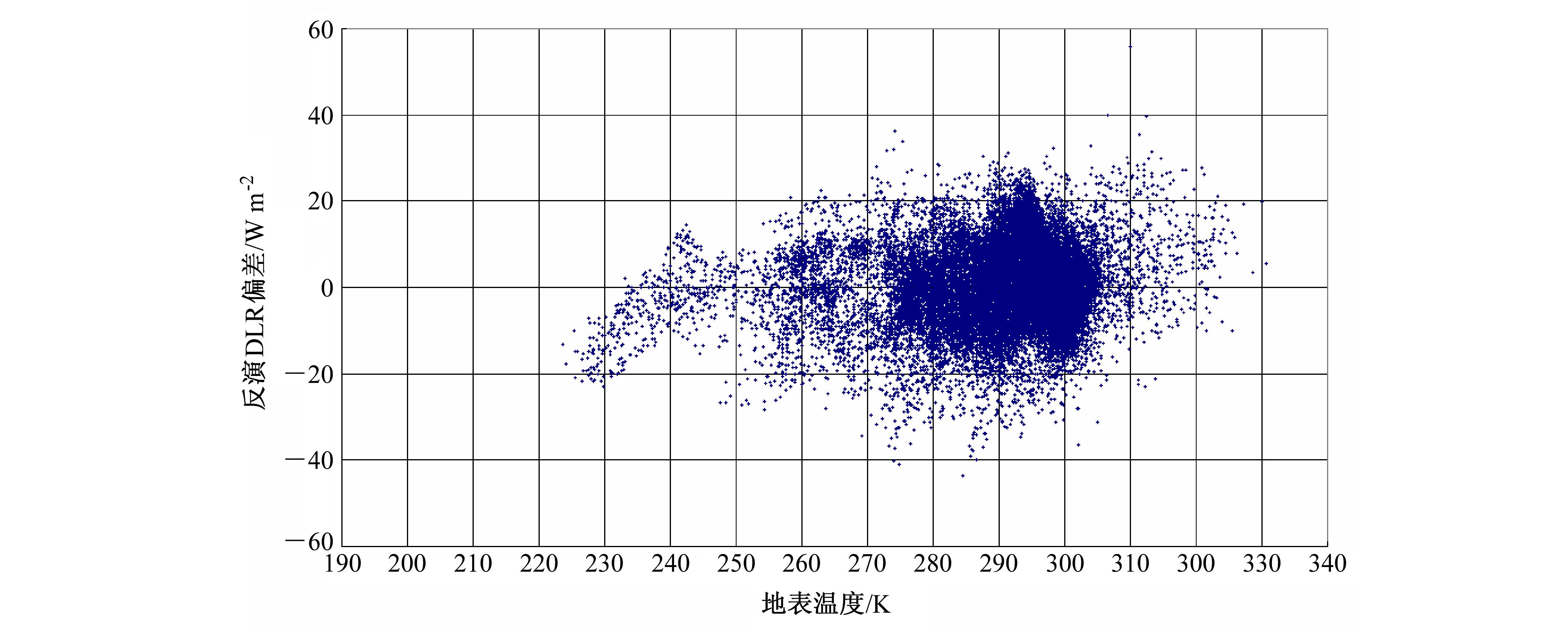图 5 模式估算DLR与模拟DLR的差值随地表温度的分布Fig. 5 The residual plot of the modeled and estimated DLR(Downward Longwave Radiation)varying with surface temperaure

4 模式应用的初步结果

由于目前尚处于FY-4产品算法研制阶段，所使用的试验资料均是Meteosat-8的SEVIRI(Spring Enhanced Visible and Infared Imger)仪器(通道光学特性与FY-4 IMAGER类似)观测数据，因此重复以上模式建立过程，我们建立了SEVIRI的DLR反演模式，利用模式和2006年8月1日00:00(协调世界时，下同)、06:00、12:00、18:00的SEVIRI L1数据文件，处理了卫星覆盖范围(45°S～45°N，45°W～45°E)，数据分辨率为0.25°(纬度)×0.25°(经度)的DLR，并用相同时间的ECMWF 6 h预报场资料地面气温和地面水汽压数据，经验计算了这一区域的DLR，气象经验计算公式如下(Wang K C and Liang， 2009)：

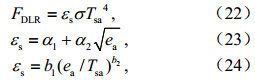
其中，Tsa是地面气温，ea是地面水汽压，a1=0.605，b1=1.24，b2=0.1429，地表海拔小于1000 m用式(23)，地表海拔大于1000 m用式(24)。图 6是SEVIRI资料反演的DLR与ECMWF经验计算结果的比较，图中 RMS分别是12.1、13.0、20.7、12.5 W/m2，发现误差最大出现在正午12:00，主要由于这时撒哈拉沙漠剧烈增温，沙漠和南非大陆地区的空气温度与地表温度差距很大，而仪器通道亮温[不论是SEVIRI通道14(通道中心波数930 cm−1)还是通道16(通道中心波数752 cm−1)]或多或少均受地表温度影响，由模式反演出的低层平均气温高于真实大气温度，计算出的DLR大大偏高，这是DLR反演模式自身的结果，这一误差在GOES-R的地表下行长波通量产品中也反映明显(Lee，2010)，GOES-R的DLR产品误差有日变化规率，12:00至14:00最大。

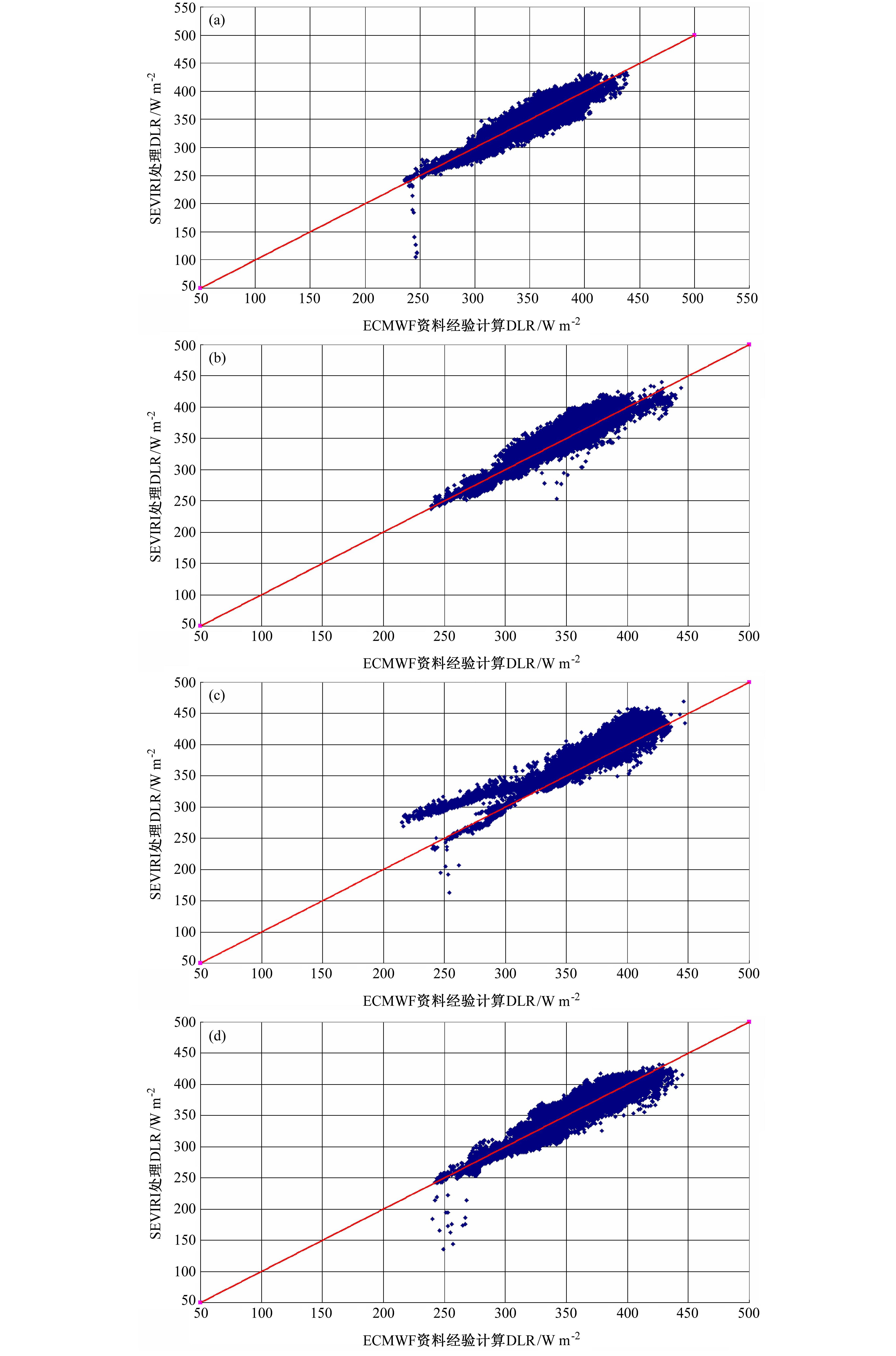图 6 SEVIRI处理DLR与ECMWF资料经验计算DLR比较(图中卫星反演DLR<250 W/m2的点为受云影响的卫星反演值)：(a)2006年8月1日00:00；(b)2006年8月1日06:00；(c)2006年8月1日12:00；(d)2006年8月1日18:00Fig. 6 Comparison between the DLR estimated with SEVIRI observations and that calculated empirically by ECMWF data(DLR less than 250 W/m2 were the satellite observations contaminated by clouds):(a)0000 UTC 1 Aug 2006;(b)0600 UTC 1 Aug 2006;(c)1200 UTC 1 Aug 2006;(d)1800 UTC 1 Aug 2006

5 结论

目前国际上用于业务的DLR统计回归模式有2种，一是线性模式：用卫星多通道辐射率的线性组合直接反演DLR(比如MODIS的DLR反演模式)，其物理原理是不同波段的通道辐射率包含了地球大气不同高度上的温度和水汽信息，MODIS DLR反演选用了6～7个通道的辐射率，模式生成的产品精度为RMS=16～25 W/m2，这一结果显然还不能满足气候研究要求(月平均DLR RMS<10 W/m2)；而第二种非线性模式采用了黑体辐射定律，把大气视为一个整体，其温度与比辐射率可由卫星通道辐射观测来反演得到，美国GOES-R的DLR反演模式及本文的DLR反演模式基本上是根据这一思路来建立的，与GOES-R不同的是本文选用了FY-4通道14、12来直接反演低层大气的温度。

本文根据黑体辐射定律，给出了计算地表下行长波辐射通量的基本方程，通过对全球大气廓线的辐射传输计算，模拟了地表下行长波辐射通量及FY-4卫星IMAGER仪器通道亮温，应用回归分析得到了通道亮温与低层大气有效辐射温度的统计关系，以及低层大气比辐射率与大气柱总可降水量的统计关系，建立了由卫星通道观测估算地表下行长波辐射通量的反演模式。将建立的SEVIRI DLR模式初步应用于Meteosat-8卫星SEVIRI仪器观测数据，处理了大西洋及非洲和地中海地区的DLR，把处理结果与由ECMWF预报场资料通过气象经验公式计算得到的DLR比较，RMS在12～20 W/m2，由于预报场资料本身及经验公式计算的DLR与真实尚有一些差异，我们预计将来FY-4的DLR产品误差会比现在试验的更小一些，从文中DLR模式自身RMS以及初步产品验证结果看来，FY-4卫星的DLR产品将满足气候研究的需求。由于地球表面的辐射能量收支决定了地表的热状况以及海洋与大气的环流运动，卫星地表长波辐射产品对于改善气候模式、长期天气预报模式将具有重要的应用价值。

本文模式尚有需要改进之处：由一个FY-4 IMAGER通道14亮温回归低层各层大气温度，误差不免较大，如果仪器通道增多，增加在900 hPa、700 hPa的温度探测通道，通过多元线性回归低层大气温度，将改进模式精度、减小模式的RMS；另

外红外辐射传输模拟计算也有进一步精确的必要。


致谢  感谢国家“千人计划”的科学家李俊博士对本文的完成给予了极大的帮助。

参考文献
[1] Darnell W L, Gupta S K, Staylor W F. 1983. Downward longwave radiation at the surface from satellite measurements [J]. J. Climate Appl. Meteor., 22 (11): 1956-1960.
[2] Ellingson R G. 1995. Surface longwave fluxes from satellite observations: A critical review [J]. Remote Sensing of Environment, 51 (1): 89-97.
[3] Lee H T. 2010. Downward longwave radiation-surface [C].//GOES-R 2010 AWG Annual Meeting, Proceedings of the Meeting, Madison, WI, 2010.
[4] Lee H T, Ellingson R G. 2002. Development of a nonlinear statistical method for estimating the downward longwave radiation at the surface from satellite observations [J]. J. Atmos. Oceanic Technol., 19 (10): 1500-1515.
[5] Matricardi M, Saunders R. 1999. Fast radiative transfer model for simulation of infrared atmospheric sounding interferometer radiances [J]. Applied Optics, 38 (27): 2367-2393.
[6] Tang B H, Li Z L. 2008. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data [J]. Remote Sensing of Environment, 112 (9): 3482-3492.
[7] Wang K C, Liang S L. 2009. Global atmospheric downward longwave radiation over land surface under all-sky conditions from 1973 to 2008 [J]. J. Geophys. Res., 114 (D19): D19101.
[8] Wang W H, Liang S L. 2009. Estimation of high-spatial resolution clear-sky longwave downward and net radiation over land surfaces from MODIS data [J]. Remote Sensing of Environment, 113 (4): 745-754.
[9] Wark D Q, Yamamoto G, Lienlsch J H. 1962. Methods of estimating infrared flux and surface temperature from meteorological satellites [J]. J. Atmos. Sci., 19 (5): 369-384.
[10] 吴晓. 1998. 地球大气透过率及辐射率计算 [J]. 应用气象学报, 9 (1): 124-128. Wu Xiao. 1998. Calculation of earth atmospheric transmissivity and radiance [J]. Quarterly Journal of Applied Meteorology (in Chinese), 9 (1): 124-128.