2 聊城大学环境与规划学院, 聊城252059
2 School of Environment and Planning, Liaocheng University, Liaocheng 252059
当前e指数地形指数模型TOPMODEL(Topographic Index Model,以下简称为经典的e指数TOPMODEL)已被应用于陆面过程模式研究中,对改善陆面过程模式模拟水文过程、从而提高陆面过程模型性能起到了一定的作用(Stieglitz et al.,1997;Gedney and Cox,2003;Douville,2003,2004;Niu et al.,2005;Reto et al.,2007)。早期发展的经典e指数TOPMODEL虽有较好的物理基础,但包含使其应用范围受到较大限制的若干假设,其中饱和导水率随土壤深度变化服从e指数分布和流域性质为空间均匀(假定流域土壤表层饱和导水率K0、导水率有效衰减系数m和地下水补给速率R等物理参数空间均匀)是两个十分重要的限制性假设(Beven and Kirkby,1979;Beven,2000)。由于实际下垫面的饱和导水率随深度变化并不一定服从e指数规律,而且实际下垫面的流域性质一般为非均匀的,为了今后有可能将地形指数模型更好、更真实地用于全球和区域气候模式的陆面模式中,放宽经典的e指数TOPMODEL假设限制、拓宽其应用范围的研究显得十分必要。Saulnier et al.(1997)推导了m在空间上可变情况下的e指数TOPMODEL;Duan and Miller(1997)、Iorgulescu and Musy(1997)、Wang et al.(2006)推导了均匀下垫面下的土壤饱和导水率随土壤深度作幂指数变化的地形指数模型(后简称幂指数TOPMODEL)。这些研究都从不同方向拓宽了地形指数模型的应用范围,但并没有完全脱离均匀下垫面的限制。在上述研究工作的基础上,Deng and Sun(2010)推导了K0、m、R空间可变的e指数TOPMODEL和幂指数TOPMODEL。对于非均匀下垫面的e指数TIOPMODEL,已有研究工作(Deng and Sun,2010),本文针对非均匀下垫面下的幂指数TOPMODEL进行K0、m和R空间非均匀条件下流域水量平衡的模拟,研究分析K0、m和R的空间变化对流域水量平衡模拟结果的影响。同时利用已有的非均匀下垫面下的e指数TOPMODEL模拟结果,对两种不同地形指数模型在空间非均匀条件下模拟结果的异同作一初步比较,为发展合理简化便于应用于大尺度陆面过程模型的地形指数水文模型提供依据。
2 下垫面性质非均匀的幂指数TOPMODEL作者在Saulnier et al.(1997)推广的m可变的e指数TOPMODEL和Duan and Miller(1997)提出的空间均匀的幂指数TOPMODEL的工作基础上,放弃了K0、m和R空间均匀的假定,推导出空间各点的土壤饱和导水率K0i、衰减系数mi和地下水补充速率Ri都可随空间变化的空间非均匀的幂指数TOPMODEL的理论关系(Deng and Sun,2010),以下给出主要的关系表达式:
(1)局地的土壤饱和缺水量Di与流域平均土壤饱和缺水量 之间的关系(Deng and Sun,2010):
之间的关系(Deng and Sun,2010):
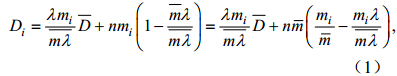
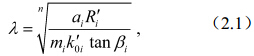

 为流域面积)的比值,即
为流域面积)的比值,即 是i点处单位面积地下水补给速率。k'0i为k0i与流域平均土壤表层饱和导水率
是i点处单位面积地下水补给速率。k'0i为k0i与流域平均土壤表层饱和导水率 的比值,
的比值, 为mi的流域平均值,ai为流经坡面任一点i处沿等高线单位长度的上坡汇流面积,βi为i点处地面的坡降梯度。当mi、K0i、Ri空间均匀时,公式(1)~(3)返回到空间均匀的幂指数分布的地形指数模型公式。
为mi的流域平均值,ai为流经坡面任一点i处沿等高线单位长度的上坡汇流面积,βi为i点处地面的坡降梯度。当mi、K0i、Ri空间均匀时,公式(1)~(3)返回到空间均匀的幂指数分布的地形指数模型公式。
(2)基流:
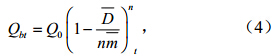
 =0时的基流,t为时刻。
=0时的基流,t为时刻。
(3)退水曲线为
1)当n>1,有
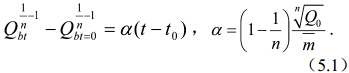
2)当n=1,有
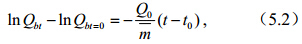
由公式(1)~(3)可得各种mi、K0i、Ri组合情况下地形指数及相应的Di公式。本文仅给出以 下几种mi、K0i、Ri不同组合情况下的地形指数及相应的Di公式:
(1)当mi、K0i、Ri均不随空间变化时,地形指数为TIO,根据公式(1)~(3)有
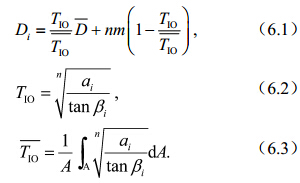
(2)当mi、K0i、Ri均随空间变化时,地形指数为TIKRM,根据公式(1)~(3)有
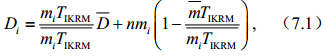
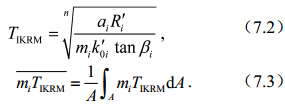
(3)当mi、Ri不随空间变化而K0i空间非均匀时,地形指数为TIK,根据公式(1)~(3)有

(4)当mi、K0i不随空间变化而Ri空间非均匀时,地形指数为TIR,根据公式(1)~(3)有

(5)当K0i、Ri不随空间变化而mi空间非均匀时,地形指数为TIM,根据公式(1)~(3)有

关于下垫面性质空间非均匀对流域水量平衡影响,从局地的土壤饱和缺水量与流域平均土壤饱和缺水量之间的关系可以看出它们都与地形指数值[见公式(7.2)、(8.2)、(9.2)和(10.2)]大小和分布密切相关。所以首先要分析对于特定流域、特定的下垫面性质空间非均匀对于地形指数值大小和分布的影响。为进行敏感性分析,本文对幂指数地形指数模型中K'0i、mi、R'i空间分布形式做以下假定:
对于mi采用Saulnier et al.(1997)的假定,mi随海拔高度hi线性减小。

 产生各点的mi,经归一化后的mi满足
产生各点的mi,经归一化后的mi满足 。将根据退水曲线确定的m作为m,本文中研究对象梭磨河流域有长年观测数据,可得该河流域的m(取4~10月的60 mm和5~9月的39 mm),分别生成mi的空间分布。
。将根据退水曲线确定的m作为m,本文中研究对象梭磨河流域有长年观测数据,可得该河流域的m(取4~10月的60 mm和5~9月的39 mm),分别生成mi的空间分布。
饱和导水率大小与土壤质地有关,土壤质地粗饱和导水率大,土壤质地细饱和导水率小。从河源到河口水流搬运能力下降,沉积物颗粒从河源到河口逐渐变细。因此假定k'0i随海拔高度hi线性增加(Deng and Sun,2010),由下式先计算出k'0i的分布:
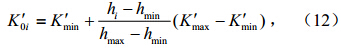
获得各点的k'0i,统计出流域平均值k0,然后由k'0i=k'0i/k0产生各点的k'0i,经归一化后的k'0i满足流域平均等于1的条件。
地形指数大的区域地下水埋深浅,水分易于补充地下水,因此假定补给速率r'i随经典的地形指数r'线性增加,先由下式计算出 的空间分布(Deng and Sun,2010):
的空间分布(Deng and Sun,2010):

本文研究流域为位于长江上游地区的梭磨河流域,其流域面积为2500 km2,平均海拔4000 m,流域内海拔最高处约5200 m,最低海拔约2600 m,是一典型的森林山区流域(Sun and Deng,2004)。由于幂指数TOPMODEL中n和m可有不同组合,在这里以n=16和m(4~10月为60 mm、5~9月为39 mm)为例来说明这种影响。根据公式(11)-(13)规定产生的k'0i、mi、R'i的空间分布和上述的m和n(=16)取值,可由公式(6.2)计算原始地形指数TIO,由公式(7.2)、(8.2)、(9.2)和(10.2)分别计算出各种地形指数和TIKRM、TIK、TIR和TIM值,其分布列于表 1(m取值39 mm),图 1则给出这些地形指数的分布函数(m取值39 mm),m大小变化对地形指数分布的影响比mi间变化产生的影响要弱;m取值60 mm生成的mi和m取值39 mm生成的mi,相应的地形指数分布差异并不大(图略)。
|
|
表 1 各种地形指数的分布 Table 1 Distributions of topographic indices |
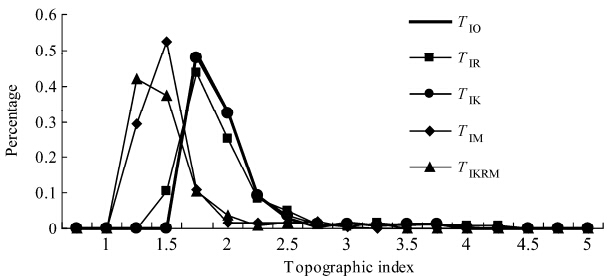 | 图 1 5种情形的地形指数分布 Fig. 1 Distribution curves of topographic indices for five cases |
从表 1和图 1可以看出由公式(11)~(13)设定的mi、Koi和Koi分布使该流域的地形指数分布函数有以下几个特点:1)TIK和TIR的分布与TIO分布差异并不大,但TIK和TIR分布函数的峰值低于TIO分布函数的峰值,而它们的地形指数值分布范围比TIO宽,可发现地形指数值在4.0~5.0范围内TIO的百分比已接近为0.0,而TIK和TIR的百分比还高于0.0,说明由公式(12)和(13)设定的Koi和R'i空间分布增加了地形指数高值区的百分比;2)TIM的最大值、最小值和平均值明显小于TIO的最大值、最小值和平均值,其分布函数的峰值高于TIO分布函数的峰值,峰值出现的位置向地形指数减小的方向偏移,这表明mi的空间变化使地形指数分布变得集中;3)在该流域中,mi的空间非均匀性对地形指数分布的影响比Koi和R'i空间非均匀性要显著,所以TIKRM的分布与TIM很接近,只是分布曲线的峰值稍小于TIM,同样TIKM和TIRM的分布也与TIKRM很相似(图略)。
3.2 空间非均匀对梭磨河流域水量平衡影响的敏感性试验本研究以经典的e指数TOPMODEL 的FORTRAN程序TOPT9502.for(TOPMODEL DEMONSTRATION PROGRAM VERSION 95.02,revised for distribution 1995 by Keith Beven)为基础进行调正改建,发展成适用于空间非均匀下垫面的幂指数分布的TOPMODEL程序。对于空间非均匀下垫面的幂指数分布,将经典e指数分布TOPMODEL中Di和Qbt表达式改写成空间非均匀的幂指数分布TOPMODEL中Di和Qbt表达式,即用公式(1)~(10.3)分别取代e指数分布TOPMODEL相应的公式。同时经典e指数模型中地形指数TIC=lnαi/tanβi也换成非均匀下垫面的幂指数分布导出的相应的地形指数(如TIK、TIR、TIM、TIKRM等)。为了估计非饱和区对地下水的补给量R,还增嵌了简单的陆面过程模型的子程序块(Sun and Deng,2004),它耦合植被截留对到达地面的降水和冠层截留和蒸发的影响,也考虑了降水透过土壤大孔隙和土壤裂隙的补给(bypassing or channeling flow)功能对非饱和层土壤湿度的影响(Sun and Deng,2004),在TOPMODEL中所需的非饱和层对饱和层的补给量ri则是由以下的经验公式来计算(Beven,2000):

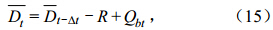
模型主要参数有:冠层的最大截留量SD和到达土壤表面的降水补给根系层下非饱和层蓄水量的比例PMAX,根系层的最大持水量SRZMAX,td,流域平均土壤饱和缺水量为零时的地表以下径流Q0、参数m,模型参数列于表 2(Sun and Deng,2004)。
|
|
表 2 TOPMODEL模型参数值 Table 2 Values of parameters of TOPMODEL model |
为研究空间非均匀对水量平衡模拟结果的影响,根据上述的n(n=16)值和设定的空间非均匀的K'oi、mi、R'i求得的梭磨河流域各种地形指数分布函数,对该流域4种不同空间非均匀性所对应的地形指数(TIK、TIR、TM和TIKRM等)进行模拟研究,通过与空间均匀的模拟结果的比较,分析空间非均匀对水文模拟结果产生的影响。
由模型相应的公式(6.1)-(10.1)计算Di,然后根据表 2给定的参数值,分别模拟了梭磨河流域1960~1999年逐日流量。计算中需对整个流域按地形指数离散成N分块,各个分块的mi值可取mi在该分块内的统计平均值,然后用于计算每个分块相应的平均Di。
从40年的模拟结果来看,与空间均匀的地形指数TIO模拟结果相比较,流域4种不同地形指数(TIK、TIR、TIM和TIKRM)模拟的逐日流量是有差异的,但差异各不相同,这说明TIK、TIR、TIM和TIKRM所对应的空间非均匀性对逐日流量有影响且影响程度各不相同。这里以1992年为例具体说明。图 2给出了TIO、TIK、TIR、TIM和TIKRM模拟的1992年逐日流量,可以看出TIR和TIK模拟的该年逐日流量比较接近,但与TIM和TIKRM模拟的逐日流量有一定的差别。再与TIO模拟的1992年逐日流量相比较,TIR、TIK的模拟结果与TIO的结果差别较小,但TIM和TIKRM模拟的洪峰流量明显高于TIO的模拟值,说明是否考虑下垫面非均匀性对于模拟水文过程会带来不同的结果。为了进一步了解空间非均匀对地表径流和地下径流的影响,图 3给出了TIR、TIK、TIM和TIKRM模拟的1992年逐日地表径流深与TIO模拟的地表径流深之差,图 4给出了TIR、TIK、TIM和TIKRM模拟的1992年逐日基流深与TIO模拟的基流深之差。一年中TIK模拟的地表径流深有时大于有时又小于TIO模拟的地表径流深,TIR和TIM模拟的地表径流深总体说来大于TIO模拟的地表径流深,说明不同的下垫面非均匀对地表径流的影响是不相同的。至于空间非均匀性对逐日基流的影响,与地表径流深呈相反趋势。
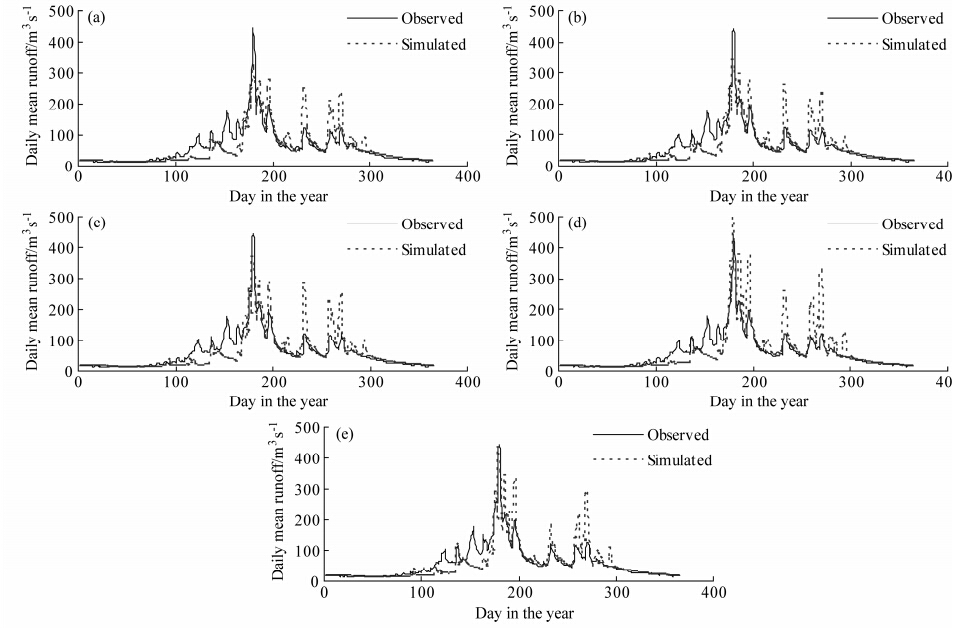 | 图 2 地形指数(a)TIO、(b)TIR、(c)TIK、(d)TIM、(e)TIKRM模拟的逐日流量 Fig. 2 Simulated daily runoffs for different topographic indices(a)TIO,(b)TIR,(c)TIK,(d)TIM,and (e)TIKRM |
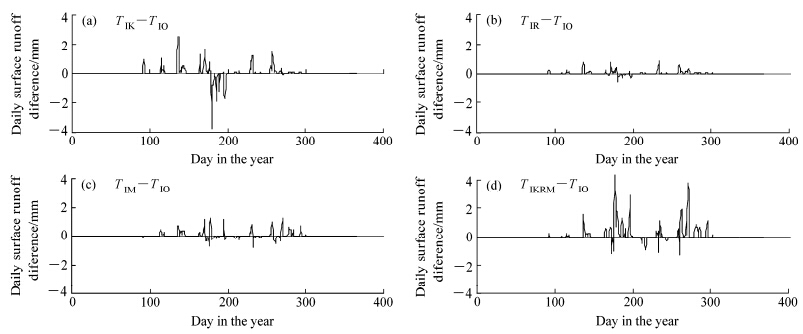 | 图 3 空间非均匀性对逐日地表径流深的影响 Fig. 3 The impacts of spatial heterogeneity on daily surface runoff simulations |
 | 图 4 同图 3,但为基流 Fig. 4 Same as Fig. 3,but for baseflow simulations |
再看空间非均匀性对流域水文过程各分量多年平均结果的影响。表 3是下垫面非均匀性下TIK、TIR、TIM和TIKRM模拟的流域40年平均的年蒸散发E、年地表径流深Qof、年基流深Qb、年总径流深Q以及年平均水量平衡的余量,其中N是模拟时流域的分块数。
|
|
表 3 地应力预测地震实例 Table 3 Examples of earthquake prediction based on field stress measurement |
由表 3 可见:1)对于多年平均的地表径流深,TIR明显高于TIO的模拟结果,TIM略高于TIO的模拟结果,TIK和TIKRM的模拟结果与TIO的模拟结果很接近。2)对于多年平均的基流,TIR模拟的基流明显低于TIO,TIM模拟的基流则高于TIO的,TIK和TIKRM模拟的基流与TIO的模拟结果接近。3)对于多年平均的年总径流深,由于地表径流和基流的互补作用,下垫面非均匀性下的TIK、TIR、TIM和TIKRM的模拟结果相差不大,与均匀下垫面对应的TIO的模拟结果差别也不大,相较之下,TIM的总径流深高于TIO的,且差别最大,TIR的总径流深则小于TIO,差别次之,TIK与TIO差别很小。4)对流域总蒸发,下垫面非均匀性的模拟结果相互间以及与均匀下垫面对应的TIO的模拟结果差别均不大。5)总体说来,K0i空间变化对水量平衡各分量影响较小;Ri的空间变化改变了地形指数分布函数,增加了地表径流而减小了基流;mi的空间变化一方面改变了地形指数的分布,另一方面也改变土壤饱和导水率随土壤深度衰减大小,这两方面变化的综合效果影响地表径流和基流的模拟结果,在这个流域数值试验中,mi的空间变化对水量平衡各个分量多年平均的模拟结果影响显得并不大。与非均匀的e指数TOPMODEL模拟结果比较,在相同的K0i、mi、Ri的空间非均匀分布下,mi的空间变化明显增加了地表径流而减小了基流,地表径流深增加了55.6 mm,约增加了50%,而基流减小了50.2 mm(Deng and Sun,2010)。而在相同的K0i、mi、Ri的空间非均匀分布下,单独的mi的空间变化或者K0i、mi、Ri的联合变化对n取值16的幂指数TOPMODEL模拟的地表径流和基流结果的影响明显小于对e指数TOPMODEL模拟结果的影响。至于两类模型对空间非均匀性尤其是对mi空间变化的敏感程度表现出的明显差异的内在原因,还有待于进一步的分析研究。
4 结论(1)对于幂指数TOPMODEL,R0i的空间变化改变了地形指数分布函数,明显增加了多年平均年地表径流深而减小了多年平均基流。
(2)K0i的空间变化对地形指数分布以及多年 平均年地表径流深和基流的模拟结果影响均不大。
(3)mi的空间变化明显影响了地形指数的分布,但对多年平均年水量平衡各分量的模拟结果 影响不及R0i的空间变化的影响,这与e指数TOPMODEL模拟结果很不一样。
(4)由于地表径流与基流的互补作用,K0i、R0i和mi的空间变化对流域多年平均年总径流和多年平均年蒸发模拟结果影响不大。
(5)K0i、R0i和mi的空间变化对流域逐日地表径流,基流和总径流模拟结果有影响,但影响程度不一。以上的工作仅是来自一个特定的流域,而且设定的K0i、mi、Ri的变化也是一特例,所以得到结果的适用性还有待在其他流域应用中进一步分析研究。
| [1] | Beven K J, Kirkby M J. 1979. A physical based variable contributing area model of basin hydrology [J]. Hydrological Science Bulletin, 24 (1): 43-69. |
| [2] | Beven K J. 2000. Rainfall-Runoff Modelling [M]. New York: John Wiley & Sons., LTD. |
| [3] | Deng H P, Sun S F. 2010. Extension of TOPMODEL applications to the heterogeneous land surface [J]. Advances in Atmospheric Sciences, 27 (1): 164-176. |
| [4] | Douville H. 2003. Assessing the influence of soil moisture on seasonal climate variability with AGCMs [J]. Journal of Hydrometeorology, 4: 1044-1066. |
| [5] | Douville, H. 2004. Relevance of soil moisture for seasonal atmospheric predictions [J]. Climate Dyn., 22: 429-446. |
| [6] | Duan J F, Miller N L. 1997. A generalized power function for the subsurface transmissivity profile in TOPMODEL [J]. Water Resour. Res., 333 (11): 2559-2562. |
| [7] | Gedney N, Cox P O. 2003. The sensitivity of globle climate model simulations to the representation of soil moisture heterogeneity [J]. Journal of Hydrometeorology, 4: 1265-1275. |
| [8] | Iorgulescu I, Musy A. 1997. Generalization of topmodel for a power law transmissivity profile [J]. Hydrological Processes, 11 (9): 1353-1355. |
| [9] | Niu G Y, Yang Z L, Dickinson R E, et al. 2005. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models [J]. J. Geophys. Res., 110, D21106, doi: 10.1029/ 2005JD006111. |
| [10] | Reto S, Vidale P L, Boone A, et al. 2007. Impact of scale and aggregation on the terrestrial water exchange: Inregrating land surface models and rhone catchment observations [J]. Journal of Hydrometeorology, 8 (5): 1002-1015. |
| [11] | Saulnier G, Beven K, Obled C. 1997. Including spatially variable effective soil depths in TOPMODEL [J]. J. Hydrol., 202: 158-1721. |
| [12] | Stieglitz M, Rind D, Famiglieth J, et al. 1997. An efficient approach to modeling the topographic control of surface hydrology for regional and global climate modeling [J]. J. Climate, 10 (1): 118-137. |
| [13] | Sun S F, Deng H P. 2004. A study of rainfall-runoff response in a catchment using TOPMODEL [J]. Advances in Atmospheric Sciences, 21 (1): 87-95. |
| [14] | Wang J, Endreny T A, Hassett J M. 2006. Power function decay of hydraulic conductivity for a TOPMODEL-based infiltration routine [J]. Hydrological Processes, 20: 3825-3834. |
 2014, Vol. 19
2014, Vol. 19




