2 解放军93811部队, 兰州730020
2 No. 93811 Unit of People's Liberation Army, Lanzhou 730020
20世纪80年代以来,在许多陆面试验和通量观测站中发现地表能量存在明显的不闭合现象,不闭合度接近20%(Wilson et al.,2002;李正泉等,2004;Oncley et al.,2007;Foken,2008)。这一现象与自然界普遍存在的能量守恒定律是相悖的,从而使地表能量不闭合问题受到了气象学家的广泛关注。大量研究表明,地表能量不闭合现象在很大程度上与地表土壤热通量计算不准确有关(Heusinkveld et al.,2004;Gao,2005;左金清等,2010;缪育聪等,2012;徐自为等,2013)。因此,研究不同土壤热通量计算方法的优劣及其对地表能量闭合度的影响具有重要意义。
目前,地表土壤热通量的计算方法有很多种,这些方法大致可以分为两类。一类是基于热传导方程通过积分土壤温湿廓线来计算地表土壤热通量,如PlateCal法(Liebethal et al.,2005)、TDEC法(阳坤和王介民,2008)。另一类是根据土壤温度的振幅、相位随土壤深度的变化特点来推算地表土壤热通量,如谐波法(Heusinkveld et al.,2004)、热传导对流法(范新岗和汤懋苍,1994;Gao,2005)、振幅法和相位法(Bhumralkar,1975)。此外,还有经验法(张立杰等,2006)、双层热传导模型(魏东平等,1992)等。
国内外许多学者基于以上计算方法研究了地表土壤热通量对地表能量闭合度的影响。Heusinkveld et al.(2004)使用谐波法计算了干旱区沙丘的地表土壤热通量,发现该方法对土壤温度和热通量的计算效果比较理想,地表能量闭合度高达96%。Jacobs et al.(2008)对比了PlateCal法和谐波法对地表能量闭合度的影响,结果表明谐波法的计算结果更好。Gao(2005)使用热传导对流法计算了西藏那曲地区的地表土壤热通量,并指出该方法相比PlateCal法提升了地表能量闭合度。左金清等(2010)使用PlateCal法、TDEC法、谐波法计算了半干旱草地的地表土壤热通量,发现TDEC法与谐波法的计算结果比较接近,与PlateCal法的偏差达到9%左右。赵静(2013)分析了PlateCal法、TDEC法在干湿不同条件下对地表能量闭合度的影响,结果表明从干燥条件到湿润条件,TDEC法对地表能量闭合度的提升更大。左洪超等(2012)认为大气运动越接近湍流时,近地层能量越接近于闭合;并在此基础上研究了PlateCal法和TDEC法得到的地表能量闭合度与相对垂直湍强的关系,发现地表土壤热通量计算方法会影响地表能量闭合度的大小,但不影响能量闭合度决定于大气运动状态的本质。这些研究表明,不同计算方法计算的土壤热通量存在显著差异,当然也会对地表能量闭合度产生显著影响。研究造成计算土壤热通量差异的原因是加深理解土壤内物质和能量传输的关键。这种差异主要由3部分原因引起,首先,不同计算方法的理论差异,如谐波法和热传导对流法分别将土壤温度看作是多个正弦波的叠加和单个正弦波的变化;其次,这种差异还与复杂的地表状况有关,如植被覆盖、根系吸水、非均匀下垫面等的影响;最后还可能与观测资料的准确程度有关。为此本研究利用在均匀裸土下垫面的观测资料来比较现有几种方法计算土壤热通量的性能,以期揭示哪种计算方法计算更准确、且具有更好的适用性。
本文利用“内蒙古微气象观测蒸发试验”的观测资料,采用6种热通量计算方法,即PlateCal法(PlateCal Method,PCM)、TDEC法、谐波法(Harmonic Method,HM)、热传导对流法(Conduction−Convection Method,CCM)、振幅法(Amplitude Method,AM)和相位法(Phase Method,PM),开展有关土壤热流量计算及其对近地层能量闭合影响的研究。首先对这6种方法的计算结果进行详细对比,分析了6种方法在不同干湿地表状况下的适用性,最后研究了这6种方法计算地表土壤热通量的差异及其对地表能量闭合度的影响。
2 观测试验和资料处理 2.1 试验简介“内蒙古微气象观测蒸发试验”位于中国内蒙古自治区阿拉善左旗巴润霍德乡(37°45′N,103°55′E),该地区处在中国西北干旱区,腾格里沙漠南缘。该地区年平均降水量为185.8 mm,年平均气温为6.0~8.5 °C。试验下垫面是均匀平坦的戈壁荒漠,植被以稀疏的骆驼刺为主,并有零星的蒿类低矮杂草。观测场的地理位置和下垫面状况如图 1所示。
 | 图 1 观测场的(a)地理位置及(b)下垫面状况Fig. 1(a)Location and (b)underlying surface of the observation field |
本次试验的观测期为2012年6月21日至9月27日。在试验观测场内架设有梯度观测塔、涡动相关观测系统(EC)、四分量辐射计、自动气象站、土壤观测系统等,观测项目包括近地层的基本气象要素、物质通量、能量通量以及土壤温湿度等。试验中所用仪器的详细情况如表 1所示。
| 表 1 相关仪器的描述和安装情况Table 1 Description and installation of the related instruments |
涡旋相关系统的观测需要建立在湍流平稳、气象要素水平均匀、近地面层存在常通量层、仪器能够观测到各种尺度的涡旋等假设基础上。但实际观测中,这些条件难以满足,如大气运动的非定常、仪器安装倾斜等。为了控制观测数据的质量,保证湍流数据的可靠性和有效性,利用英国爱丁堡大学发明的EdiRE 软件对采样频率为10 Hz的原始湍流数据进行了再处理。处理过程包括:野点去除(Hojstrup,1993;Vickers and Mahrt,1997)、坐标旋转(Wilczak et al.,2001)、时间延迟订正、超声虚温订正(Kaimal and Gaynor,1991)、频率损失订正(Massman,2000; Massman and Lee,2002)和WPL订正(Webb et al.,1980)等。最后根据涡旋相关理论(Swinbank,1951),平均时间取30 min,计算出各时间段内的平均感热通量和潜热通量等物理量。
3 研究方法 3.1 土壤热通量计算方法现有地表土壤热通量计算方法大多都是基于一维热传导方程发展而来。土壤的一维热传导方程为
| $\frac{{\partial {\rho _{\rm{s}}}{c_{\rm{s}}}T}}{{\partial t}} = - \frac{{\partial G}}{{\partial z}}$ | (1) |
| $G = - \lambda \frac{{\partial T}}{{\partial z}}$ | (2) |
| ${\rho _{\rm{s}}}{c_{\rm{s}}} = {\rho _{\rm{d}}}{c_{\rm{d}}}(1 - {\theta _{{\rm{sat}}}}) + {\rho _{\rm{w}}}{c_{\rm{w}}}\theta $ | (3) |
PlateCal法(Liebethal et al.,2005)通过积分土壤中的储存热,并将其叠加到热通量板的观测结果上得到地表土壤热通量。在TDEC法(阳坤和王介民,2008)中,将地表和土壤底层的观测温度作为一维热传导方程的上下边界条件求解土壤温度廓线,然后利用实测土壤温度资料对求解出的温度廓线进行校正,得到一个更合理的温度廓线,最后积分土壤温湿廓线得到地表土壤热通量。谐波法(Heusinkveld et al.,2004)是将一维热传导方程公式(2)代入公式(1)从而得到一个关于土壤温度的方程,将其上边界条件取为傅里叶级数的形式并计算土壤温度的解析解,把土壤温度的解析解代入公式(2)即得到土壤热通量的计算式。热传导对流法(Gao,2005)是考虑到一维热传导方程虽然描述了土壤中的分子热传导过程,但土壤中的水分运动造成的热量传输也不可忽视(Gao et al.,2003),因而该方法耦合了土壤中的热传导和热对流过程。振幅法和相位法(Bhumralkar,1975)与谐波法类似,但求解土壤温度方程时的上边界条件是正弦函数的形式,且这两种方法分别根据土壤温度的振幅
和相位计算土壤热扩散率$\kappa $($\kappa = \lambda /{\rho _{\rm{s}}}{c_{\rm{s}}}$,单位:${{\rm{m}}^2}{\rm{ }}{{\rm{s}}^{ - 1}}$)。
6种土壤热通量计算方法在计算过程中使用的观测数据如表 2所示。其中,地表温度(T0)根据向上、向下长波辐射反演得到,即
| ${T_0} = {\left[ {\frac{{{R_{{\rm{lu}}}} - (1 - {\varepsilon _{\rm{g}}}){R_{{\rm{ld}}}}}}{{{\varepsilon _{\rm{g}}}\sigma }}} \right]^{\frac{1}{4}}},$ | (4) |
| 表 2 不同热通量计算方法的数据使用情况Table 2 Data used by different soil heat flux calculation approaches |
地表能量平衡表达式一般写为(Wilson et al.,2002;Oncley et al.,2007):
| ${R_{\rm{n}}} - {G_0} = H + {L_{\rm{E}}}$ | (5) |
采用能量平衡比率(EBR)表示地表能量闭合度的大小:
| ${E_{{\rm{BR}}}} = \frac{{H + {L_{\rm{E}}}}}{{{R_{\rm{n}}} - {G_0}}}$ | (6) |
为了避免平均风较小时,垂直湍强会变得异常大的影响,采用相对垂直湍强(RIw)表征大气湍流的强度(左洪超等,2012):
| ${R_{{\rm{Iw}}}} = \frac{{\sqrt {\overline {{{w'}^2}} } }}{{\sqrt {\overline {{{w'}^2}} } + \overline u }}$ | (7) |
采用均方差(RMS)对计算结果进行误差分析:
| ${R_{{\rm{MS}}}} = \sqrt {\frac{1}{N}\sum\limits_{j = 1}^N {{{({x_i} - {y_i})}^2}} } $ | (8) |
“内蒙古微气象观测蒸发试验”使用的HFP01SC型热通量板具有一定的在线自校正功能(http://www.hukseflux.com/downloads/thermalScience/applicAndSpec.pdf[12]),且观测精度较高(Van Loon et al.,1998;Cobos and Baker,2003)。本实验在土壤2 cm处埋设有此种型号的热通量板,所以可以用不同方法计算2 cm处的土壤热通量,通过与观测结果的比较来评价不同方法的优劣。计算过程中使用的2 cm土壤温度,由地表和5 cm土壤温度线性插值得到。选取2012年6月22~26日无降水情况下共5 d的数据,比较6种土壤热通量计算方法的性能。并选取6月27~29日、7月14~16日、8月1~3日的数据,分析6种方法在不同干湿地表状况下的适用性。
4.1.1 不同方法的计算性能利用PlateCal法、TDEC法、谐波法、热传导对流法、振幅法和相位法计算2 cm土壤热通量,计算值与观测值的比较如图 2和3所示。由图 2可以看出,6种方法计算的2 cm土壤热通量与观测值的日变化趋势一致,不同方法的最大差别可以达到119.9 W/m2。其中,PlateCal法计算的2 cm土壤热通量与观测值最接近。TDEC法、谐波法和热传导对流法的计算结果比较一致,但在白天和夜间都比观测值(绝对值)偏大较多。振幅法和相位法计算的土壤热通量都是正弦波的形式,白天与观测值的变化趋势基本一致,但在夜间与观测值相差较大。
 | 图 2 2 cm土壤热通量计算值与观测值对比Fig. 2 Comparison of calculated and observed soil heat fluxes at 2-cm depth |
2 cm土壤热通量计算值与观测值的散点对比图如图 3所示。图 3表明,PlateCal法计算的土壤热通量与观测值相比在1:1线附近均匀分布。TDEC法、谐波法和热传导对流法的计算结果偏大。振幅法和相位法在夜间(G<0时)明显偏离1:1线,计算结果偏小。从均方差和相关系数来看,PlateCal法计算的2 cm土壤热通量与观测值相关性最好,相关系数为0.99,均方差最小,为6.9 W/m2。TDEC法、谐波法和热传导对流法的计算结果分别比观测值偏大41%、39%、46%,均方差都在30.0 W/m2左右,但相关系数都在0.97以上。振幅法和相位法计算的2 cm土壤热通量与观测值的相关性较差,相关系数分别为0.91和0.90,均方差分别为28.8 W/m2和28.0 W/m2。通过比较可以看出,PlateCal法计算的2 cm土壤热通量与观测值最接近。
 | 图 3 2 cm土壤热通量(a)PlteCal法、(b)TDEC法、(c)谐波法、(d)热传导对流法、(e)振幅法、(f)相位法计算值与实测值散点图Fig. 3 Scatter diagram of calculated soil heat fluxes from(a)PlateCal method,(b)TDEC method,(c)harmonic method,(d)conduction−convection method,(e)amplitude method,and (f)phase method versus measured soil heat fluxes at 2-cm depth |
以上对比分析表明,不同热通量计算方法计算的2cm土壤热通量存在明显差异。下面对计算结果存在差异的可能原因从土壤温度、土壤热参数和土壤环境的复杂性3个方面进行简单讨论。
土壤温度会影响土壤热通量的准确计算。PlateCal法直接使用观测温度计算土壤热通量,但浅层土壤温度变化剧烈,用观测温度计算的平均土壤温度可能难以反映土壤的实际热力状况;TDEC法根据一维热传导方程计算土壤温度廓线,然后用观测温度对其进行校正,最终得到的温度廓线与实际情况较为接近;谐波法根据谐波理论将土壤温度的变化看作是多个正弦波的叠加,对土壤温度的计算精度较高(Heusinkveld et al.,2004);热传导对流法、振幅法、相位法用正弦波描述土壤温度的变化,计算误差的大小取决于实际温度的变化是否接近于正弦波的形式。6种热通量计算方法在温度计算方面存在差异,导致最终得到的温度廓线及其日变化会有明显区别,从而影响土壤热通量的计算。
土壤热参数对土壤热通量的计算结果也有影响。土壤热参数包括土壤热容量、热传导系数、热扩散率等。土壤热容量一般由公式(3)计算,6种方法之间不存在差异,但TDEC法需要计算深层土壤热容量,土壤热容量的计算误差主要来源于土壤孔隙度,下层土壤孔隙度设置偏小会导致土壤热容量偏大,这可能是TDEC法计算结果偏大的主要原因。热传导系数表征土壤传递热量的能力,TDEC法涉及土壤热传导系数,但该方法对土壤热传导系数不敏感(阳坤和王介民,2008),一般将其给定为一常数1.0${\rm{W }}{{\rm{m}}^{ - {\rm{1}}}}{\rm{ }}{{\rm{K}}^{ - 1}}$。土壤热扩散率是表征土壤热力性质的重要参量,热传导对流法将土壤的热传导和热对流作用分开考虑,计算的热扩散率只包含热传导作用(高志球等,2002);振幅法和相位法根据土壤温度的振幅和相位信息估算热扩散率,计算方法粗略;而谐波法在计算过程中充分利用土壤温度信息,并且对土壤温度的计算精度较高,因此,谐波法的计算结果通常作为土壤热扩散率的最优估计(缪育聪等,2012)。谐波法、热传导对流法、振幅法和相位法计算的平均土壤热扩散率分别为$3.66 \times {10^{ - 7}}$、$1.78 \times {10^{ - 7}}$、$2.15 \times {10^{ - 7}}$、$1.80 \times {10^{ - 7}}$ ${{\rm{m}}^2}{\rm{ }}{{\rm{s}}^{ - 1}}$ $$,可以看出,热传导对流法、振幅法和相位法计算的平均土壤热扩散率比谐波法分别偏小51.4%、41.3%和50.8%。此外,热传导对流法需要计算土壤水通量密度,其计算结果为$4.4 \times {10^{ - 7}}$ ${\rm{m }}{{\rm{s}}^{ - 1}}$,但该方法是使用单一的正弦波拟合土壤温 度来估算水通量密度,准确性较差,而且仅计算水通量密度的日平均值,不能反应其日变化(缪育聪等,2012),该方法还有待改进。
土壤环境的复杂性也会影响土壤热通量的计算。现有热通量计算方法大多基于0~5 cm的土壤观测资料计算地表热通量,0~5 cm土壤层较薄,但其温度、湿度变化剧烈,加上干湿变化、季节变化以及植被覆盖等因素的影响,给浅层土壤热通量的测量和计算带来很大不确定性。另外,一些热通量计算方法假设整层土壤各向同性,如谐波法、振幅法和相位法,这些方法更容易受到土壤环境复杂性的影响。
4.1.2 6种方法在不同干湿地表状况下的适用性为了进一步研究这6种热通量计算方法在不同干湿地表状况下的适用性,在相对干燥、相对湿润和降水条件下各选取3 d数据作为典型个例(图 4),对比6种方法在不同干湿地表条件下的计算性能。从图 4可以看出,7月14~16日感热占主导(图 4a),可以作为干燥条件;8月1~3日潜热较大(图 4b),可以作为湿润条件;6月27~29日存在密集降水(图 4c),可以作为降水条件进行分析。
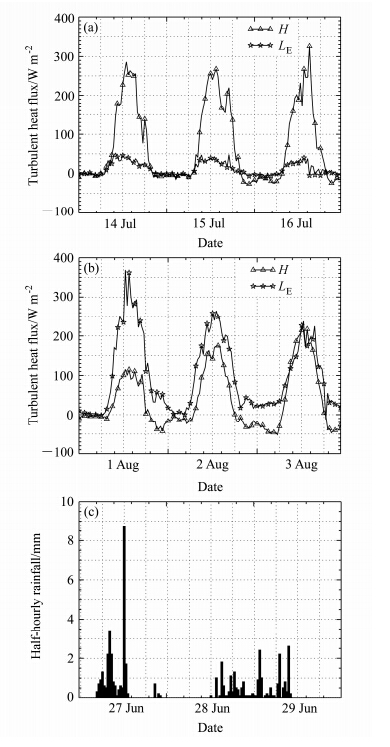 | 图 4 反映不同干湿地表状况的典型个例:(a)干燥条件;(b)湿润条件;(c)降水条件Fig. 4 Typical examples for different surface conditions:(a)Dry condition;(b)wet condition;(c)rainy condition |
| 表 3 干燥、湿润和降水条件计算2 cm土壤热通量计算值与观测值的均方差和相关系数Table 3 Root-mean-square errors and correlation coefficients of the calculated and measured soil heat fluxes at 2-cm depth under dry,wet,and rainy conditions |
干燥、湿润和降水条件下,6种方法计算的2 cm土壤热通量与实测值的比较如图 5和表 3所示。结合图 5和表 3可以看出,干燥条件下(图 5a),PlateCal法的计算结果与观测值最接近,均方差为14.0 W/m2,相关系数为1.00。其他方法计算2 cm土壤热通量的特征与前面的分析结果基本一致。湿润条件下(图 5b),谐波法计算的2 cm土壤热通量与观测值最接近,均方差最小,为21.4 W/m2,与观测值的相关性也最好,相关系数为0.98。而PlateCal法、TDEC法和热传导对流法的计算结果比观测值(绝对值)偏大,振幅法和相位法的计算结果比观测值偏小。降水条件下(图 5c),PlateCal法的计算结果与观测值最接近,均方差最小,为30.1 W/m2,与观测值的相关性也相对较好,相关系数为0.93。其他方法的计算结果与观测值偏离较多。
 | 图 5(a)干燥、(b)湿润和(c)降水条件下的2 cm土壤热通量Fig. 5 Soil heat fluxes at 2-cm depth in(a)dry,(b)wet,and (c)rainy conditions |
对比6种方法计算地表土壤热通量的差异,仍然采用6月22~26日的数据。6种方法计算的地表土壤热通量如图 6所示,由图可以看出,不同方法计算的地表土壤热通量的特征和2 cm土壤热通量情况基本一致,只是地表土壤热通量的变化更加剧烈。白天,热传导对流法比其他方法相位滞后,振幅法和相位法有时会相位超前(如6月23日),不同方法计算的地表热通量在12:00(北京时间,下同)左右达到最大值,6种方法之间的差别可达到100 W/m2左右;日出和日落前后,PlateCal法、TDEC法、谐波法、热传导对流法计算的向上热通量偶尔会出现峰值,这一现象在23日17:30左右最为明显;夜间,PlateCal法、TDEC法、谐波法、热传导对流法计算的地表热通量变化平稳,不同方法的差别在50 W/m2左右,而振幅法和相位法的变化趋势与其它4种方法存在明显差别。
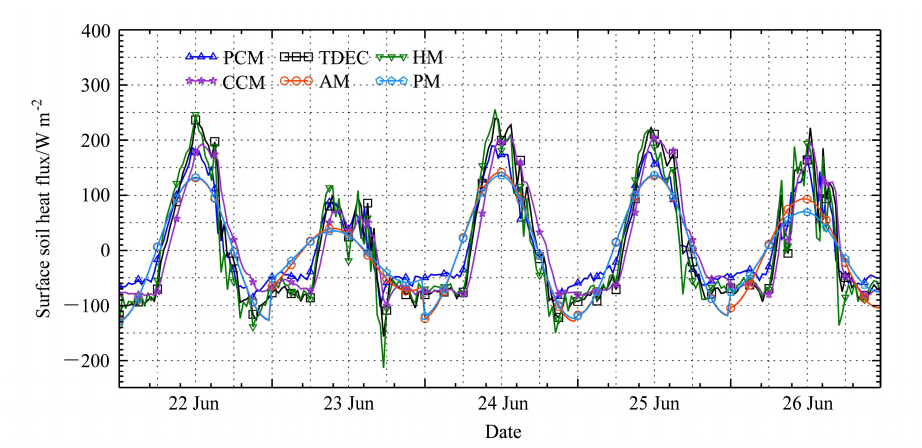 | 图 6 地表土壤热通量Fig. 6 Surface soil heat fluxes |
借助统计方法定量分析6种方法计算地表土壤热通量的差异。图 7给出了6种方法计算地表土壤热通量的最大差值相对于平均值的变化以及最大差值的频率分布。图 7a表明,6种方法计算地表土壤热通量的最大差值在17.6~178.6 W/m2之间,当平均值小于-30 W/m2时,最大差值基本在20~100 W/m2之间,平均值大于-30 W/m2时,基本在60 W/m2以上。图 7b表明,6种方法计算地表土壤热通量的最大差值主要分布在25~100 W/m2之间,占样本的83.8%,有12.5%的样本最大差值超过了100 W/m2。通过比较可以看出,6种土壤热通量计算方法对土壤热量传输过程的描述存在明显差异。由此可知,在地气相互作用涉及土壤热流量计算等问题的研究中,采用不同方法计算地表土壤热通量对研究结果会有重要影响。
 | 图 7 6种方法计算地表土壤热通量的(a)最大差值随平均值的变化及其(b)频率分布Fig. 7(a)Maximum differences between surface soil heat fluxes calculated by the six methods against the average and (b)their frequency distributions |
为了研究不同热通量计算方法对地表能量闭合度的影响,使用2012年6月21日至9月27日的数据,按照白天(Rn>0)和夜间(Rn<0)分为两组,将每组数据按照相对垂直湍强从小到大排序并分成20等份,为了避免异常值的影响,对每份数据取0~1范围内的EBR闭合度计算平均值,并将每份数据的相对垂直湍强平均值作为该份数据的相对垂直湍强,进而分析不同热通量计算方法对地表能量闭合度的影响。
由图 8可知,对于6种土壤热通量计算方法来说,白天的闭合状况都好于夜间,不同方法得到的地表能量闭合度存在明显差异;但随着相对垂直湍强增大,6种方法得到的地表能量闭合度总体上都是增大的。当RIw增大到一定程度时,EBR闭合度随RIw增大的规律不再明显,甚至出现下降,原因可能是当近地面存在较强的垂直对流时,涡动相关系统无法完全观测到这种较大尺度的水热通量。以上结果表明不同热通量计算方法能够影响近地层能量闭合度的大小,但不会影响地表能量闭合度随湍流混合增强而增大的规律,这进一步验证了左洪超等(2012)的结论。
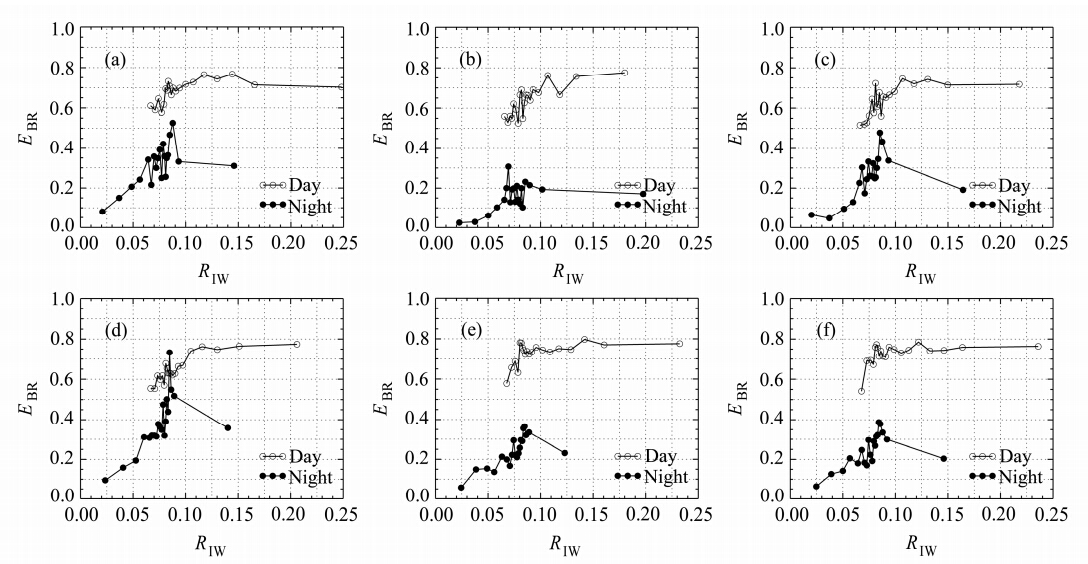 | 图 8(a)PlateCal法、(b)TDEC法、(c)谐波法、(d)热传导对流法、(e)振幅法、(f)相位法计算的EBR闭合率随相对垂直湍强(RIW)的变化Fig. 8 EBR calculated by(a)PlateCal method,(b)TDEC method,(c)harmonic method,(d)conduction−convection method,(e)amplitude method,and (f)phase method against the relative vertical turbulence intensity(RIW) |
本文利用“内蒙古微气象观测蒸发试验”的观测资料,研究了6种热通量计算方法(PlateCal法、TDEC法、谐波法、热传导对流法、振幅法和相位法)在干旱区均匀裸土下垫面的计算效果,分析了6种方法在不同干湿地表状况下的适用性,并比较了6种方法计算地表土壤热通量的差异及其对地表能量闭合度的影响。得到以下主要结论:
(1)一般情况下,PlateCal法计算的2 cm土壤热通量相对于观测值的均方差最小,为6.9 W/m2。
(2)干燥和降水条件下,PlateCal法的计算结果与观测值最接近,计算结果的均方差分别为14.0 W/m2和30.1 W/m2;湿润条件下,谐波法的计算结果与观测值最接近,计算结果的均方差为21.4 W/m2。
(3)6种方法计算地表土壤热通量的最大差别可以达到178.6 W/m2,最大差值达到25.0 W/m2以上的时次占样本的96.3%。
(4)地表土壤热通量计算方法对地表能量闭合度的大小有明显影响,但不影响近地层能量闭合度随湍流混合增强而增大的规律。
准确计算地表土壤热通量,对于深入理解陆气相互作用过程,解决近地层能量不闭合问题,改进陆面过程模式等都有重要帮助。近几年来,国内外的许多学者针对土壤热通量计算方法做了大量研究,并取得了重要成果。本研究在均匀裸土下垫面比较6种土壤热通量计算方法,试图在消除复杂下垫面影响的基础上,研究不同土壤热通量计算方法的性能。研究表明,通常情况下,PlateCal法计算土壤热通量的精度较高,但在不同的干湿地表状况下,其计算性能又会受到影响,如干燥条件下,PlateCal法的计算结果较好,湿润条件下,谐波法的计算精度反而较高,而降水情况下,6种方法的计算误差都比较大。这表明现有土壤热通量计算方法尚不能稳定可靠地描述土壤中的热量传输过程,准确计算土壤热通量仍然存在诸多困难。为了更好地研究土壤热通量计算方法,今后可以在实验室开展不同土壤热通量计算方法的对比试验。在控制某些变量(如土壤质地、有机质含量等)的基础上,对不同土壤热通量计算方法展开更为详细和深入的对比研究,进而发展一种更加稳定可靠的土壤热通量计算方法。
| [1] | Bhumralkar C M. 1975. Numerical experiments on the computation of ground surface temperature in an atmospheric general circulation model [J]. J. Appl. Meteor., 14 (7): 1246-1258. |
| [2] | Cobos D R, Baker J M. 2003. In situ measurement of soil heat flux with the gradient method [J]. Vadose Zone Journal, 2 (4): 589-594. |
| [3] | 范新岗, 汤懋苍. 1994. 土壤传导—对流热通量计算的初步结果 [J]. 高原气象, 13 (1): 14-19. Fan Xingang, Tang Maocang. 1994. A preliminary study on conductive and convective soil heat flux [J]. Plateau Meteorology (in Chinese), 13 (1): 14-19. |
| [4] | Foken T. 2008. The energy balance closure problem: An overview [J]. Ecological Applications, 18 (6): 1351-1367. |
| [5] | Gao Z Q. 2005. Determination of soil heat flux in a Tibetan short-grass prairie [J]. Bound.-Layer Meteor., 114 (1): 165-178. |
| [6] | 高志球, 卞林根, 张雅斌, 等. 2002. 土壤热传导方程解析解和那曲地区土壤热扩散率研究 [J]. 气象学报, 60 (3): 352-360. Gao Zhiqiu, Bian Lingen, Zhang Yabin, et al. 2002. Study on analytical resolution to soil thermal conductive equation and soil thermal diffusivity over Nagqu area [J]. Acta Meteorologica Sinica (in Chinese), 60 (3): 352-360. |
| [7] | Gao Z Q, Fan X G, Bian L G. 2003. An analytical solution to one-dimensional thermal conduction-convection in soil [J]. Soil Science, 168 (2): 99-107. |
| [8] | Heusinkveld B G, Jacobs A F G, Holtslag A A M, et al. 2004. Surface energy balance closure in an arid region: Role of soil heat flux [J]. Agricultural and Forest Meteorology, 122 (1-2): 21-37. |
| [9] | Hojstrup J. 1993. A statistical data screening procedure [J]. Measurement Science and Technology, 4 (2): 153-157. |
| [10] | Jacobs A F G, Heusinkveld B G, Holtslag A A M. 2008. Towards closing the surface energy budget of a mid-latitude grassland [J]. Bound.-Layer Meteor., 126 (1): 125-136. |
| [11] | Kaimal J C, Gaynor J E. 1991. Another look at sonic thermometry [J]. Bound.-Layer Meteor., 56 (4): 401-410. |
| [12] | 李正泉, 于贵瑞, 温学发, 等. 2004. 中国通量观测网络(ChinaFLUX)能量平衡闭合状况的评价 [J]. 中国科学(D辑), 34(增刊II):46-56. Li Zhengquan, Yu Guirui, Wen Xuefa, et al. 2005. Energy balance closure at China FLUX sites [J]. Science in China (Ser. D), 48 (Suppl. II): 51-62. |
| [13] | Liebethal C, Huwe B, Foken T. 2005. Sensitivity analysis for two ground heat flux calculation approaches [J]. Agricultural and Forest Meteorology, 132 (3-4): 253-262. |
| [14] | Massman W J. 2000. A simple method for estimating frequency response corrections for eddy covariance systems [J]. Agricultural and Forest Meteorology, 104 (3): 185-198. |
| [15] | Massman W J, Lee X. 2002. Eddy covariance flux corrections and uncertainties in long-term studies of carbon and energy exchanges [J]. Agricultural and Forest Meteorology, 113 (1-4): 121-144. |
| [16] | 缪育聪, 刘树华, 吕世华, 等. 2012. 土壤热扩散率及其温度、热通量计算方法的比较研究 [J]. 地球物理学报, 55 (2): 441-451. Miao Yucong, Liu Shuhua, Lü Shihua, et al. 2012. A comparative study of computing methods of soil thermal diffusivity, temperature and heat flux [J]. Chinese Journal of Geophysics (in Chinese), 55 (2): 441-451. |
| [17] | Oncley S P, Foken T, Vogt R, et al. 2007. The energy balance experiment EBEX-2000. Part I: Overview and energy balance [J]. Bound.-Layer Meteor., 123 (1): 1-28. |
| [18] | Swinbank W C. 1951. The measurement of vertical transfer of heat and water vapor by eddies in the lower atmosphere [J]. Journal of Atmospheric Sciences, 8: 135-145. |
| [19] | Van Loon W K P, Bastings H M H, Moors E J. 1998. Calibration of soil heat flux sensors [J]. Agricultural and Forest Meteorology, 92 (1): 1-8. |
| [20] | Vickers D, Mahrt L. 1997. Quality control and flux sampling problems for tower and aircraft data [J]. J. Atmos. Oceanic. Technol., 14: 512-526. |
| [21] | Webb E K, Pearman G I, Leuning R. 1980. Correction of the flux measurements for density effects due to heat and water vapour transfer [J]. Quart. J. Roy. Meteor. Soc., 106: 85-100. |
| [22] | 魏东平, 石耀霖, 汤懋苍, 等. 1992. 利用气象地温资料反演大地热流 [J]. 地球物理学报, 36 (6): 733-739. Wei Dongping, Shi Yaolin, Tang Maocang, et al. 1992. Calculation of heat flow from meteorological data [J]. Acta Geophysica Sinica (in Chinese), 36 (6): 733-739. |
| [23] | Wilczak J M, Oncley S P, Stage S A. 2001. Sonic anemometer tilt correction algorithms [J]. Bound.-Layer Meteor., 99: 127-150. |
| [24] | Wilson K, Goldstein A, Falge E, et al. 2002. Energy balance closure at FLUXNET sites [J]. Agricultural and Forest Meteorology, 113 (1-4): 223-243. |
| [25] | 徐自为, 刘绍民, 徐同仁, 等. 2013. 不同土壤热通量测算方法的比较及其对地表能量平衡闭合影响的研究 [J]. 地球科学进展, 28 (8): 875-889. Xu Ziwei, Liu Shaomin, Xu Tongren, et al. 2013. The observation and calculation method of soil heat flux and its impact on the energy balance closure [J]. Advances in Earth Science (in Chinese), 28 (8): 875-889. |
| [26] | 阳坤, 王介民. 2008. 一种基于土壤温湿资料计算地表土壤热通量的温度预报校正法 [J]. 中国科学(D辑), 38 (2): 243-250. Yang Kun, Wang Jiemin. 2008. A temperature prediction-correction method for estimating surface soil heat flux from soil temperature and moisture data [J]. Science in China (Ser. D), 51 (5): 721-729. |
| [27] | 张立杰, 江灏, 李磊. 2006. 利用气象要素计算五道梁地区土壤热流量的试验 [J]. 高原气象, 25 (3): 418-422. Zhang Lijie, Jiang Hao, Li Lei. 2006. A test of the soil heat flux calculation in Wudaoliang area using meteorological elements [J]. Plateau Meteorology (in Chinese), 25 (3): 418-422. |
| [28] | 赵静. 2013. 干湿状况下黄土高原半干旱区荒草下垫面能量闭合特征 [D]. 兰州大学硕士学位论文, 24-46. Zhao Jing. 2013. The characteristics of energy balance closure under wet/dry conditions over native grassland in semi-arid loess plateau [D]. M. S. Thesis (in Chinese), Lanzhou University, 24-46. |
| [29] | 左洪超, 肖霞, 杨启东, 等. 2012. 论近地层大气运动特征与观测和计算能量不平衡的成因 [J]. 中国科学(D辑), 42 (9): 1370-1384. Zuo Hongchao, Xiao Xia, Yang Qidong, et al. 2012. On the atmospheric movement and the imbalance of observed and calculated energy in the surface layer [J]. Science China (Ser. D), 55 (9): 1518-1532. |
| [30] | 左金清, 王介民, 黄建平, 等. 2010. 半干旱草地地表土壤热通量的计算及其对能量平衡的影响 [J]. 高原气象, 29 (4): 840-848. Zuo Jinqing, Wang Jiemin, Huang Jianping, et al. 2010. Estimation of ground heat flux for a semi-arid grassland and its impact on the surface energy budget [J]. Plateau Meteorology (in Chinese), 29 (4): 840-848 |
 2015, Vol. 20
2015, Vol. 20




