2 湖南省防雷中心,长沙 410007
3 南京信息工程大学,南京 210044
4 山西省人工降雨防雹办公室,太原 030002
2 Hunan Province Lightning Protection Centre, Changsha 410007
3 Nanjing University of Information Science and Technology, Nanjing 210044
4 Shanxi Province Weather Modification Office, Taiyuan 030002
雨滴谱观测是云和降水物理观测研究的重要项目之一,通过地面雨滴谱准确测量单点降水、直接获取观测资料,可以分析降水的物理结构及其演变特征,对于进一步研究降水微观物理过程有着重要的意义(黄美元和徐华英,1999;郭学良等,1999;胡朝霞等,2003;濮江平等,2007)。利用天气雷达可以连续监测大范围降水及其分布,而在较小体积范围内、较小尺度的降雨,天气雷达的探测能力有限,其在定量测量小降水方面存在很大的不确定性。自从Marshall and Palmer(1948)提出雨滴谱分布模型以来,寻找不同自然云雨的滴谱分布以及雷达反射率因子Z与降雨率R之间的Z-R关系一直是云降水物理学中的重要研究课题。因此,通常需要联合雨滴谱和雷达,来定量估测降水分布和降水量。
雷达定量测量降水的理论虽然开始很早,但是直到20世纪70年代后期雷达数字化技术迅速发展之后,研究工作才有坚实的基础。目前雷达测量降水主要依据是雷达反射率因子Z与降雨率R之间的Z-R关系式,关键技术之一是Z-R关系式参数的准确确定。关于Z-R关系的论述,国内已有不少报道,但所用雨滴谱资料大多是滤纸法得到(如,张培昌等,2001;班显秀等,2008a;冯雷和陈宝君,2009)。染色滤纸法简单方便,一直受到广泛使用,利用其观测资料统计Z-R关系也有报道,但其不足之处在于会发生大滴的溅散和雨滴重叠,同时工作量大(冯雷和陈宝君,2009),且时效性差,不能实时地反馈信息。而激光雨滴谱仪,能够连续自动观测,可获取大量的观测样本,其对小滴段的观测令人满意,近年来得到国内广泛使用(濮江平等,2007;班显秀等, 2008a,2008b)。并且,激光雨滴谱仪能实时地将雨滴谱样本数据传输至计算机,可供快速处理,并可与远端的雷达扫描信息进行融合,提高雷达定量测量降水的能力,因此在科学技术高速发展的今天将有更为广阔的应用前景。
研究发现,当雨滴直径大于1 mm时,雨滴在下落过程中会发生明显的形变,由圆球形变成椭球状或者扁球状(Brandes et al., 2002)。偏振雷达正是利用了扁球体的扁率对水平入射波和垂直入射波的作用不同来获取反射率差及差分传播相位移等偏振参数(Bringi and Ch and rasekar, 2001)。同时,雨滴的形状对反演雨滴谱分布及雷达估测降水量也有重要影响。可以说,雨滴轴比上较小的偏差能导致滴谱分布、降雨率测量较大的误差。因此,有必要考虑雨滴轴比对雷达参量的影响。这对于提高雷达定量估计降水精度具有重要的意义。然而,目前有关雨滴轴比对雷达参量的影响研究尚不多见且主要是理论方面的模拟研究(张培昌和刘传才,1998;吴莹等,2007),因此,有必要考虑雨滴轴比对雷达参量的影响。本文尝试性应用雨滴谱观测数据,探讨雨滴轴比订正对雷达参量及参量关系的影响,并定量给出雷达参量在雨滴轴比订正前后的关系。
考虑到后续的联合雷达估测降水,本文选取了距离山西省太原雷达站200 km范围内的祁县、介休两地2008年7、8月Parsivel激光雨滴谱仪观测数据,对比分析两地的总雨滴样本谱特征,统计雷达参量的分布概率,研究雨滴轴比订正对降雨率R、反射率因子Z的影响,确定两地的Z-R关系及反射率因子Z与雨水含量W的Z-W关系,有别于以往的理论模拟研究,同时也为当地雷达定量测量降水、人工增雨作业效果评估和雷电监测预警提供更加准确的科学数据。
2 滴谱资料来源与处理
选用山西省人工降雨防雹办公室2008年7、8月在山西省祁县、介休两地利用德国OTT公司Parsivel激光雨滴谱仪采样的数据。Parsivel激光雨滴谱仪将采样粒子的粒径和下落末速度各划分为32档[具体划分情况见文献(Loffler-Mang,1998; Loffler-Mang and Joss, 2000)],每次采样中统计1024(32×32)个档位中出现的雨滴数目。Parsivel雨滴谱仪在小滴段、小速率段的分档较细,对速率较小的小滴的观测较多,因此可以满足人们对小滴段的观测要求。本文分析了祁县、介休两地总的雨滴谱样本特征(图 1a、1b)。在图 1 a、1b中还显示了根据Brandes et al.(2002)给出了雨滴的下落末速度v和直径D之间的v-D关系曲线[具体表达式如公式(1)所示] 。由图 1可见,祁县、介休两地的雨滴样本个数n[具体表述形式见公式(2)、(3)、(4)]都集中处于一个较为连续的区域,并且此区域内雨滴的末速度v和直径D之间的v-D关系大致满足公式(1)。该结果也进一步验证了Brandes获取的v-D关系 [公式(1)]的正确性。
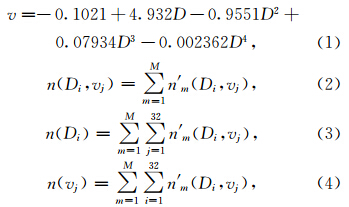
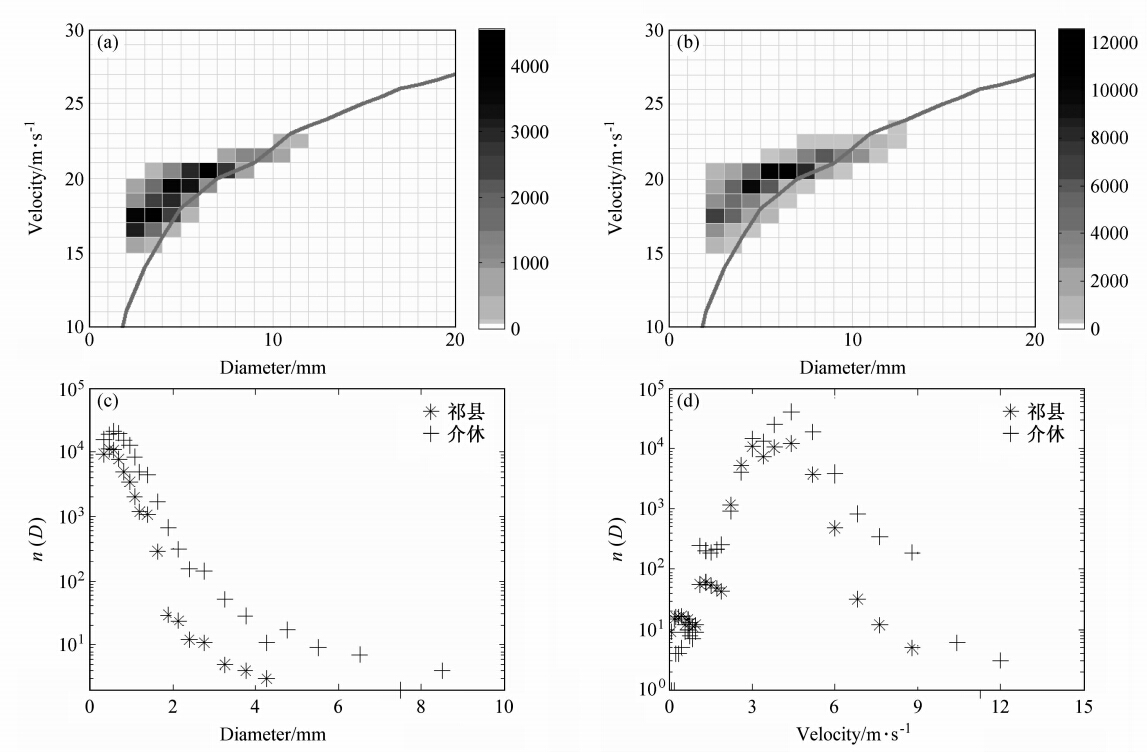 | 图 1 雨滴样本特征:(a)祁县、(b)介休的雨滴数n的样本分布图;祁县、介休的(c)尺度谱n(D)和(d)速度谱n(v)Fig. 1 Sample characteristics of raindrops: Raindrops distribution charts in(a)Qixian and (b)Jiexiu;(c)diameter distributions n(D) and (d)velocity spectra n(v) in Qixian and Jiexiu |
另外,图 1c和1d显示的是两地的尺度谱n(D)和速度谱n(v)。结果表明,尺度D在1 mm以下(第8档以下)的雨滴数目是相当多的,随着雨滴尺度的增大,雨滴数目逐渐减少。在祁县观测到的雨滴尺度D主要为1~20档,即集中于尺度0.25~5.0 mm范围,出现尺度大于5 mm的雨滴极少;就速度谱而言,祁县雨滴速度峰值出现在5 m·s-1附近,根据公式(4)的v-D关系可得出速度为5 m·s-1的雨滴尺度大致为1.0~1.6 mm范围,经过这样处理的数据结果在统计上是合理的。
比较两地总的雨滴样本谱特征发现,介休所有样本中各个档位所对应的雨滴总个数n的分布形式与祁县较为相似,而其尺度谱n(D)、速度谱n(v)则与祁县不相同,表现为:尺度分布中(图 1c),介休的谱分布比祁县的高,祁县的n(D)峰值(104 个)小于介休的峰值(2×104 个),同时介休的尺度谱较连续、尺度范围较宽,其尾巴也延伸到较大的大滴处。两地的尺度分布差异规律也适用于两地的雨滴末速度谱,但二者的速度谱峰值对比更为明显。
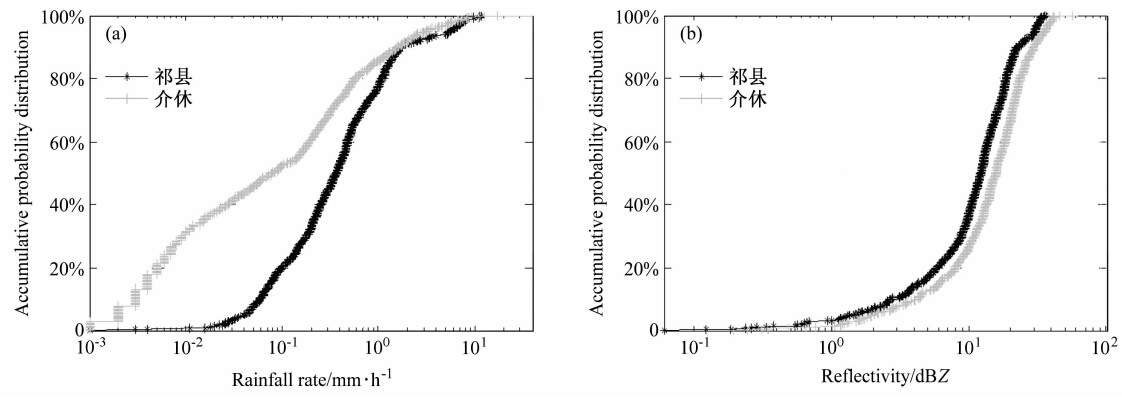 | 图 2 祁县、介休两地的累积概率分布(CPD):(a)降雨率R;(b)雷达反射率因子ZFig. 2 Cumulative probability distribution(CPD)of(a)rain rate R and (b)reflectivity Z in Qixian and Jiexiu |
为了解祁县、介休两地2008年7、8月降雨的整体状况,本文给出了两地降雨率R
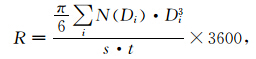
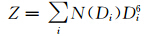
研究山西省祁县、介休两地的雨滴样本的尺度分布、速度谱分布,可初步了解两地的滴谱特征。分析两地的雷达参量的分布概率,可明确当地的季节性降水情况,为人工影响天气做科学准备工作。
3 雨滴轴比订正对降雨率R和雷达反射率因子Z的影响
大家知道,较大雨滴在下落过程中,受空气阻力作用而近似成扁椭球形,而偏振雷达正是利用雨滴水平与垂直方向的差异来获取雨滴的后向散射特性和差分传播相位移等偏振信息,进而通过这些参量反演出滴谱参数的。因此,雨滴形状和轴比对反演雨滴谱分布和偏振雷达定量估测降雨影响较大。Parsivel雨滴谱仪观测雨滴时,能测量出水平方向的尺度D,但不能给出垂直方向的尺度。因此,若直接引用测量值D代替等效体积直径Deq,就会影响滴谱的 n 矩参数Mn [ Mn=∫∞0DneqN(Deq)dDeq]计算值,而使雷达参数的计算有较大的误差。当轴比b/a=f(Deq)(a为形变雨滴水平方向上的长半轴,即雨滴谱仪和水平偏振雷达的观测值,b为垂直方向的短半轴,a、b的单位是mm)为已知时,再联合Deq=2a2/3b1/3,就可以求得等效体积直径Deq,从而实现形变订正(郑娇恒和陈宝君,2007)。
Pruppacher and Beard(1970)通过风洞试验建立了轴比函数关系:
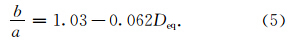
图 3和图 4分别给出了祁县、介休两地轴比订正前后的降雨速率R和雷达反射率因子Z的变化。由图可知,在祁县、介休两地,当降雨率较小时(R<1 mm·h-1),订正前后的R值相差不明显;而在降雨率R较大时(R>5 mm·h-1),订正前后差异较大,例如,R=6 mm·h-1时,祁县、介休订正后的R值分别为5.79 mm·h-1、5.53 mm·h-1,即订正后R值分别减小了3.46%、7.76%。这种随着R值增大,订正效果越明显的现象也适用于雷达反射率因子Z。当反射率因子Z=2000 mm6·m-3时,祁县、介休两地订正后的Z值变成了1773.95 mm6·m-3、1609.77 mm6·m-3,即订正后Z值分别减小了11.30%、19.51%。分析发现,由于介休采样到了更多大降雨率R的样本,降雨率R的订正效果也较祁县的更为明显(7.76%>3.46%,19.51%>11.30%)。在同一个地区中,因为受大滴的影响程度不同,Z、R变化也不一样,表现为:正比于尺度的3.67次方的R订正前后相差不大,但是正比于尺度的6次方的Z值订正前后相差较大。就整体而言,这两个参数的订正效果都随降雨率增大而越来越明显。这种参数R、Z的订正效果随降雨率增大而明显的现象,可解释为:降雨率较小的降雨过程,其小滴较多而大滴较少,小滴更接近球形,因此订正前后的雨滴尺度变化不大,因而轴比订正对降雨率R和雷达反射率因子Z的影响就较小;反之,降雨率较大的降雨过程,其大滴较多,因此订正前后的雨滴尺度变化大,轴比订正对降雨率R和雷达反射率因子Z的影响效果明显,表现在数值上都减小较多。
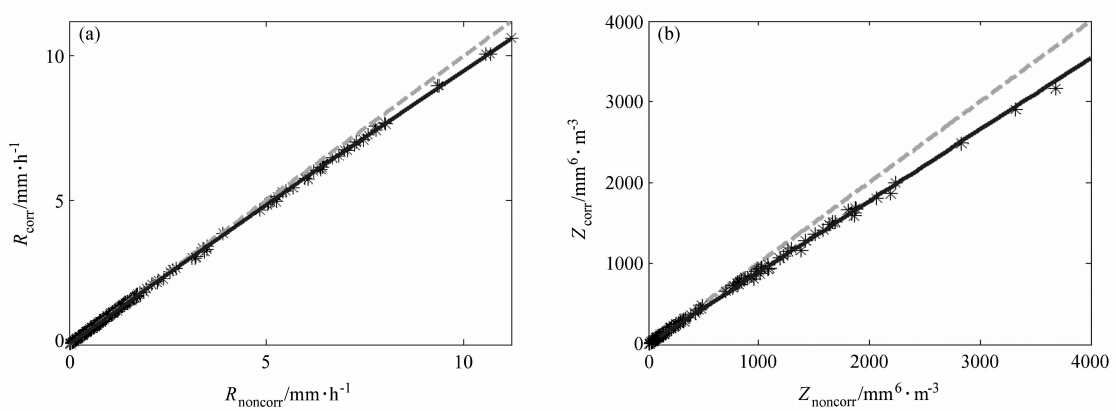 | 图 3 祁县形变订正前后(a)降雨率R、(b)反射率因子Z变化。图中,实线为线性拟合曲线,下标uncorr表示订正前的参量,corr表示订正后的参量Fig. 3 Dependences of(a)R and (b)Z upon axis ratio between noncorrection and correction at Qixian,where the solid line is for linear fitting curve,the subscript uncorr st and s for noncorrection and corr for correction |
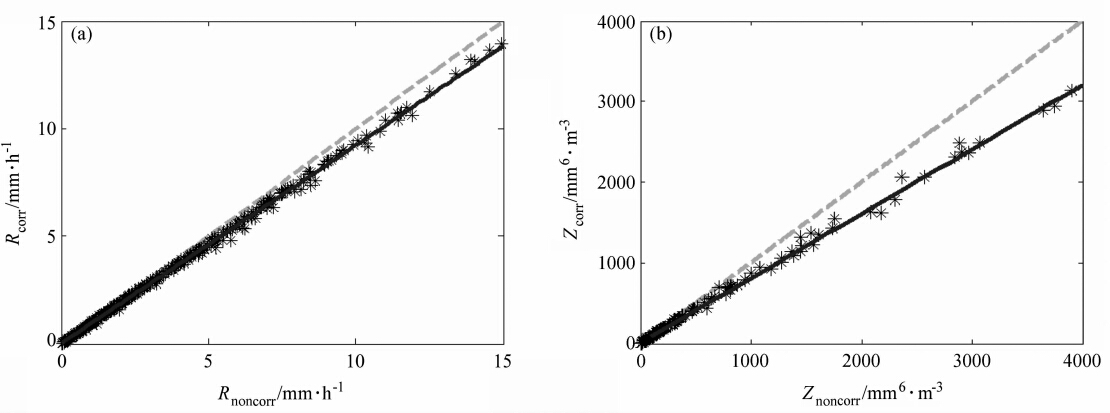 | 图 4 同图 3,但为介休Fig. 4 Same as Fig. 3,but for Jiexiu |
同时,本文也分析了祁县、介休雨滴轴比订正前、后的降雨率R之间以及雷达反射率因子Z之间的关系(见图 3和图 4),其关系分别为
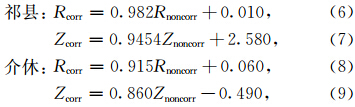
4 Z-R关系、Z-W关系研究
考虑了雨滴形状而进行形变订正后,可分析订正后的反射率因子与降雨率之间的Z-R关系、反射率因子与雨滴含水量之间的Z-W关系。在Z-R关系研究历程中,国内外研究(Mason,1971;许绍祖等,1990;)表明Z-R关系可用Z=cRd形式表示(其中,Z单位:mm6·m-3,R单位:mm·h-1,c、d是系数),其测量准确度在很大程度上取决于该Z-R关系式中系数c、d的确定。但是c、d随地点、季节以及不同降水类型而变,二者的变化范围很大(许绍祖等,1990),c变化范围为16.6~730,d的取值范围为1.16~2.87。
本文在确定Z-R关系时,将形变订正后的雨滴等效成体积相等的球体,计算了采样时间内的R值和Z值,在这里假设雨滴的电学特性是各向同性的,并且符合瑞利散射条件。根据上述观测数据,在考虑了雨滴轴比订正的基础上,对祁县、介休两地采样的多个(R,Z)数据点进行拟合得到Z-R关系。从图 5a、5b可知,介休因为降雨过程稍多,探测到极小降雨的过程(R<0.1 mm·h-1)的样本也多,其Z-R关系的离散度也稍大些(两地的曲线拟合系数平方R2分别为0.951、0.852)。祁县、介休的Z-R关系分别为:
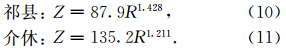
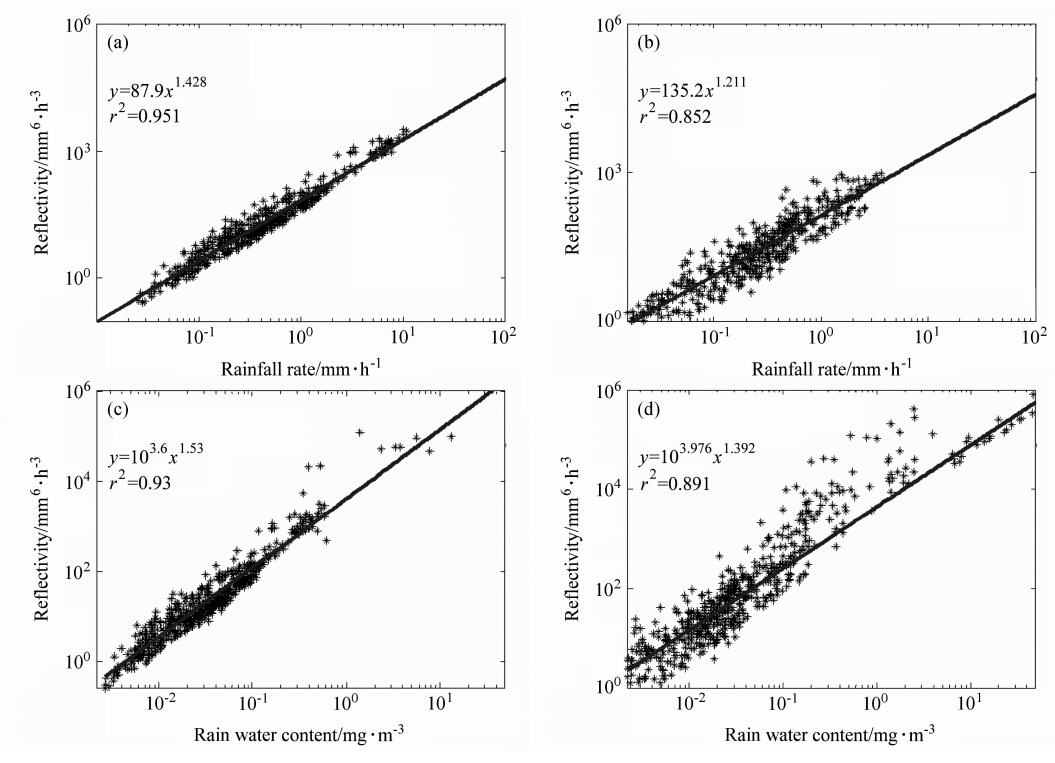 | 图 4(a、c)祁县、(b、d)介休的(a、b)Z-R关系和(c、d)Z-W关系Fig. 5(a,b)Z-R relationships and (c,d)Z-W relationships at(a,c)Qixian and (c,d)Jiexiu |
实际操作中,在缺少雷达数据的情况下,可提取雨滴谱仪的反射率因子Z观测值作为未进行订正的Znoncorr。基于轴比订正,本文也尝试研究未订正的雷达反射率因子Znoncorr与进行了订正的降雨率Rcorr之间的Znoncorr-Rcor关系,以提高雷达测量降水的精度和稳定度。祁县、介休两地的Znoncorr-Rcorr关系分别为:
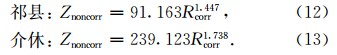
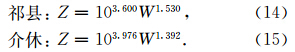
5 小结与讨论
(1)祁县、介休两地总的雨滴谱特征较为相似,但介休的谱分布较连续、雨滴分布范围相对较宽。二地的雨滴尺度范围主要集中在0.25~5.0 mm,雨滴末速度峰值出现在5 m·s-1附近,这些雨滴的v-D关系分布与Brandes et al.,(2002)所给的v-D关系式〔公式(1)〕很吻合。
(2)雨滴轴比对雷达参量影响不可忽略。在降雨率R较大(R>5 mm·h-1)时,订正前后的降雨率R大小差异较大;当降雨率较小(R<1 mm·h-1)时,差异不明显。这种规律也适用于雷达反射率因子Z。这个特征可解释为:降雨率较小的降雨过程,其雨滴尺度也不大,那么轴比订正对降雨率R和雷达反射率因子Z的影响就较小,反之,参量R、Z在进行轴比订正后会减少很多。
(3)在雨滴轴比订正的基础上,分析给出了祁县、介休两地未经过轴比订正的雷达反射率因子Z和订正后的降雨率R的Znoncorr-Rcorr关系,这对有效地联合雷达和雨滴谱仪进行定量估测降雨分布具有重要意义。
在分析大量可用数据的基础上,可探讨M-P分布、Gamma分布、有约束的Gamma分布(constrained Gamma distribution)3种分布形式对滴谱拟合的影响,它将是需要进一步研究的课题。
| [1] | 班显秀, 耿树江, 袁健. 2008a. 基于激光粒子探测仪探测结果的Z-I关系分析[J]. 安徽农业科学, 36(33): 14674-14679. Ban Xianxiu, Geng Shujiang, Yuan Jian. 2008a. Analysis on relationships of radar reflectivity and rain rate based on the raindrop spectra[J]. Journal of Anhui Agricultural Sciences (in Chinese), 36(33): 14674-14679. |
| [2] | 班显秀, 袁健, 王永亮. 2008b. 沈阳一次西风槽降水过程的雨滴谱特征分析[J]. 沈阳农业大学学报, 39(2): 145-151. Ban Xianxiu, Yuan Jian, Wang Yongliang. 2008b. Features of raindrop size distributions of a westly through in Shenyang[J]. Journal of Shenyang Agricultural University (in Chinese), 39(2): 145-151. |
| [3] | Brandes E A, Zhang G F, Vivekanandan J. 2002. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment[J]. J. Appl. Meteor., 41: 674-685. |
| [4] | Bringi V N, Chandrasekar V. 2001. Polarimetric Doppler Weather Radar: Principles and Applications[M]. Cambridge: Cambridge University Press, 636pp. |
| [5] | 冯雷, 陈宝君. 2009. 利用PMS的GBPP-100型雨滴谱仪观测资料确定Z-R关系[J]. 气象科学, 29(2): 192-198. Feng Lei, Chen Baojun. 2009. The radar reflectivity-rainrate relationships as inferred from ground-based raindrop spectra observed by GBPP-100 probe[J]. Scientia Meteorologica Sinica (in Chinese), 29(2): 192-198. |
| [6] | 郭学良, 黄美元, 徐华英, 等. 1999. 层状云的雨滴谱分档数值模拟研究[J]. 大气科学, 23(4): 411-421. Guo Xueliang, Huang Meiyuan, Xu Huaying, et al. 1999. The raindrop category model study on raindrop distribution of stratiform clouds[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 23(4): 411-421. |
| [7] | 胡朝霞, 李宏宇, 肖辉. 2003. 旬邑冰雹云的数值模拟及累积带特征[J]. 气候与环境研究, 8(2): 196-208. Hu Zhaoxia, Li Hongyu, Xiao Hui. 2003. Numerical simulation of hailstorms and the characteristics of accumulation zone of supercooled raindrops in Xunyi County[J]. Climatic and Environmental Research (in Chinese), 8(2): 196-208. |
| [8] | 黄美元, 徐华英. 1999. 云和降水物理[M]. 北京: 科学出版社, 291pp. Huang Meiyuan, Xu Huaying. 1999. Clouds and Precipitation Physics[M]. (in Chinese). Beijing: Science Press, 291pp. |
| [9] | Loffler-Mang M. 1998. A laser-optical device for measuring cloud and drizzle drop size distributions[J]. Meteorologische Zeitschrift, 7: 53-62. |
| [10] | Loffler-Mang M, Joss J. 2000. An optical disdrometer for measuring size and velocity of hydrometeors[J]. J. Atmos. Oceanic Technol., 17: 130-139. |
| [11] | Marshall J S, Palmer W. 1948. The distribution of raindrops with size[J]. J. Atmos. Sci., 5: 165-166. |
| [12] | Mason B J. 1971. The Physics of Clouds[M]. Oxford: Oxford University Press, 671pp. |
| [13] | Pruppacher H R, Beard K V. 1970. A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air[J]. Quart. J. Roy. Meteor. Soc., 96: 247-256. |
| [14] | 濮江平, 赵国强, 蔡定军, 等. 2007. Parsivel激光降水粒子谱仪及其在气象领域的应用[J]. 气象与环境科学, 30(2): 3-8. Pu Jiangping, Zhao Guoqiang, Cai Dingjun, et al. 2007. Parsivel precipitation particle spectrometer and application in meteorological realm[J]. Meteorological and Environmental Sciences (in Chinese), 30(2): 3-8. |
| [15] | 吴莹, 王振会, 陈钟荣, 等. 2007. 椭球雨滴群旋转轴呈正态分布情况时雷达反射率因子的修正[J]. 高原气象, 26(1): 128-134. Wu Ying, Wang Zhenhui, Chen Zhongrong, et al. 2007. Radar meteorological equations for groups of rotating spheroidal raindrops under normal distribution of their rotatory axes and correction for rainfall measurement[J]. Plateau Meteorology (in Chinese), 26(1): 128-134. |
| [16] | 许绍祖, 朱国江, 尹球, 等. 1990. 武汉和宜昌地区降水的Z-R关系[J].南京气象学院学报, 12(4): 572-575. Xu Shaozu, Zhu Guojiang, Yin Qiu, et al. 1990. The Z-R relationship of precipitation in Wuhan and Yichang areas[J]. Journal of Nanjing Institute of Meteorology (in Chinese), : 572-575. |
| [17] | 张培昌, 杜秉玉, 戴铁丕. 2001. 雷达气象学[M]. 北京: 气象出版社, 177-188. Zhang Peichang, Du Bingyu, Dai Tiepi. 2001. Meteorology[M]. (in Chinese). Beijing: China Meteorological Press, 177-188. |
| [18] | 张培昌, 刘传才. 1998. 旋转椭球雨滴群的雷达气象方程及测雨订正[J]. 南京气象学院学报, 21(3): 307-312. Zhang Peichang, Liu Chuancai. 1998. Radar meteorological equation for groups of rotating spheroidal raindrops and correction for rainfall measurement[J]. Journal of Nanjing Institute of Meteorology (in Chinese), 21(3): 307-312. |
| [19] | 郑娇恒, 陈宝君. 2007. 雨滴谱分布函数的选择: M-P和gamma分布的对比研究[J]. 气象科学, 27(1): 17-25. Zheng Jiaoheng, Chen Baojun. 2007. Comparative study of exponential and Gamma functional fits to observed raindrop size distribution[J]. Scientia Meteorologica Sinica (in Chinese), 27(1): 17-25. |
 2012, Vol. 17
2012, Vol. 17


