2. 兰州大学数学与统计学院,兰州 730000;
3. 兰州大学大气科学学院,半干旱气候变化教育部重点实验室, 兰州 730000
2. School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000;
3. Key Laboratory for Semi-Arid Climate Change of the Ministry of Education, College of Atmospheric Science, Lanzhou University, Lanzhou 730000
风电是世界上增长最快的可再生能源。根据欧洲风能协会和绿色和平组织签署的《关于2020年风电达到世界电力总量的12%的蓝图》的报告预测,2020年全球风电装机容量将达到12.31×109kW,风电将占到全球发电量的12%。我国风能资源十分丰富,可开发利用的风能储量约10×109kW。随着我国能源结构调整,无污染可再生的风电日益得到重视。中国丰富的风力资源及经济增长带来的能源需求增加,风机技术和规模不断进步,充分表明中国风电市场在未来10年内会以更快的速度增长(王永熙和张源,2003)。
风电场风速预报是风力发电研究中的关键问题,也是一个难题,其预测技术还有待进一步提高(雷亚洲等,2002)。随着风电场穿透功率(即风电功率占系统总发电功率的比例)的增加,风电场并网运行会给电网带来严重影响,足以破坏电力系统经济、安全、稳定、可靠运行的状态。风电的原动力是风能,而风能具有较强的随机性和波动性,使得接入电网的风电穿透功率呈现剧烈的波动特性(林海涛,2010)。对风速和风力发电功率进行准确的预测,则有利于电力系统调度部门及时调整调度计划,从而可有效地减轻风电对电网的影响,减少电力系统运行成本和旋转备用,提高风电穿透功率极限,为风电场参与发电竞价奠定基础。
目前,我国风电场风速预测的误差在25%~40%,这不仅与预测方法有关,还与预测周期以及预测地点的风速特性有关。一般来说,预测周期越短,预测地点的风速变化越缓和,预测误差就会越小;反之,预测误差就会越大(杨秀媛等,2005)。目前为风电场提供风速预报的方法主要是统计方法和数值天气预报方法。统计方法,即只根据历史数据预报风电场风速的方法,主要包括:持续法(王晓兰和李辉,2010)、卡尔曼滤波法(Bossanyi,1985)、时间序列法(Box and Jenkins, 1976;Pinson et al., 2003)、模糊逻辑算法(Alexiadis et al., 1999)、空间相关法(Barbounis et al., 2006)及人工神经网络方法(Carolin and Fernandez, 2007)等人工智能方法。统计方法只需风电场的风速时间序列即可建立模型并对风速进行预测。但是,统计方法缺少影响风速变化的动力学信息,故只能用于超短期预测,即只能预测当前时刻后一步或几步内的风速,否则预测结果很难令人满意。
在预测长度大于6 h的短期风力时,通常采用数值天气预报方法。数值天气预报在一定的初值和边值条件下,通过大型计算机作数值计算,求解描述天气演变过程的流体力学和热力学方程组,预测未来一定时段的大气运动状态(沈桐立等,2003)。数值模式能够较好地预报风电场区域风速的变化状况,较准确地捕获天气系统特征,给出较好的短期预报(孙川永等,2009)。但大气数值模式是一个离散化的数值模型,只是物理和数学意义上的近似,其描述的大气过程与真实大气过程存在误差。这种误差会随着模式积分时间的延长而增加,完全准确的数值模式不可能出现(郑飞,2007)。因此,模式误差是制约数值预报准确性提高的一个关键因素。在时间间隔为10 min的超短期风速预测中,统计方法预测的步长比较短,预测约50步后精度就开始降低了,而模式方法预测的步长较长,可以预测432步(3 d)。所以在超短期预测中,统计方法明显优于模式方法。对日平均风速预测、周平均和月平均风速预测,模式方法和统计方法效果相差无几。
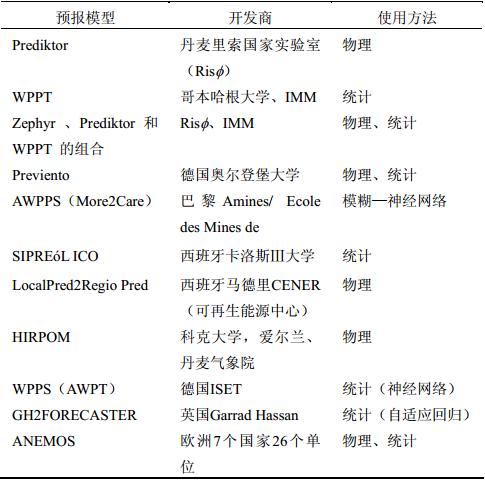
丹麦、德国、西班牙、英国及美国等风电发展较为成熟的国家,已经研发出数个用于风电场出力短期预报系统(表 1),并在多个风电场在线运行。
| 表 1 具有代表性的风电场出力短期预报系统 Table 1 The representative powerful short-term forecasting system of wind farm |
这些系统有的使用统计模型,有的使用物理模型。第一个风电场出力短期预报系统是丹麦里索国家实验室(Risφ)开发的Prediktor,使用的物理模型方法;德国有两个系统使用物理模型方法,由Eurowind GmbH开发的SOWIE系统和由Energy & meteo systems GmbH奥尔登堡大学开发的Privi- ento;美国True Wind开发的Ewind模型也是使用物理模型方法,但最后又使用自适应统计方法来消除系统误差(刘永前等,2007)。
丹麦、德国、西班牙等风电技术较发达国家,已经普遍应用风电场出力预报技术,成为欧洲国家不断提高风电比重的前提。美国近年来也在这方面投入大量研究费用,并取得了一些初步成果。与国外相比,我国还没有专门用于风电场短期风速预报的数值天气预报(NWP),短期风速预报尚处于初步探索和研究阶段。
目前我国正在发展的风电场大部分是集中在一个区域内的大型风电场。这些大型风电场对电网产生的影响必然比分散的小型风电场要大。此外,我国风资源丰富、适合建设大型风电场的地区,电网建设相对薄弱,大容量的风电接入电网,对电网的影响将更为强烈,以至于不得不采取限制风电场发电功率的措施来保证电网的安全稳定运行。
由此可见,开展风电场出力短期预报研究与开发对于我国大规模开发风电场已变得十分必要和迫切。风电场出力预报系统算法和结构与风电场的特点密切相关,欧洲和美国的系统不能直接应用到我国,必须自主研究与开发适用于我国风电场的出力短期预报系统(刘永前等,2009)。2 方法
按照风电调度以及风电厂并网的技术标准发展要求,最理想的情况是对每个风力发电机提供准确的72 h瞬时风速预报,这样就能从容地进行风电调度。事实上,这在实际操作过程中很难实现。目前一些风电发达国家的业务应24 h风速预报日平均相对误差是20%~25%,我国24 h风速预报的日平均相对误差在25%~40%之间,低于国际水平。目前国内仍然缺少成熟的风电风速预报系统,与发达国家相比存在很大差距。2.1 统计预测方法
近年来我们一直致力于风电场风速预测方法研究,针对单一统计预测模型误差较大的局限性提出了一些组合优化模型。这些组合优化模型已被成功地应用到河西走廊地区马鬃山、武威、张掖、酒泉、民勤5站点的风速预测(见表 2)。实验表明:与传统方法相比,这些组合优化模型较大地提高了该地区的风速预测精度。
| 表 2 河西走廊5站点风速预测方法及其预测误差 Table 2 The method and forecasting error of fiveobservation stations in Hexi Corridor |
相对于25%~40%这个误差范围来说,表 2所 示的3种组合优化模型都取得了较好的预测精度,在一定程度上说是风速预测又取得一大进步。通过大量的模拟实验发现:预测时间间隔越短,单位时间内所包含的预测样本点就越多,数据所体现出来的随机性以及非线性就越强,数据波动就越剧烈,规律性就越弱,这就给预测带来极大的困难。目前国内外对于时间间隔为10 min的风速预测研究很少,并且现存研究方法均难以取得良好的预测效果,该类型风速预测的研究至今还是一个世界性的难题。因此,如何有效地利用统计预测方法提高超短期风速预测精度,并对风电场及所接入的电网系统进行合理调度,就有着重大的现实意义。2.2 模式预测方法
采用WRF(Weather Research and Forecasting)模式进行数值模拟试验,重点考虑从云尺度到天气尺度等重要天气预报。该模式是一个完全可压非静力模式,控制方程组都写为张量形式。网格采用Arakawa C格点,有利于在高分辨率模拟中提高准确性;垂直方向采用地形追随气压静力坐标系统。模式采用的积分方案为Runge-Kutta 2阶和3阶时间积分方案,水平和垂直方向上采用2~6阶计算方案,对声波和重力波采用时步分离计算方案。该模式包含多种辐射、微物理、积云对流、边界层、陆面过程参数化方案,经过多次验证证明其具有优秀的气象模拟能力。
本文采用的WRF版本为WRF(ARW)3.2版。数值模拟试验模拟区域为(33.67°N~50.22°N,104.876°E~129.70°E),模拟时间为2010年4月1日08:00(北京时间,下同)至9月3日08:00,如图 1所示。图中标记处为承德红松风电场。共设计4种数值模拟实验。除方案3外,其余模拟方案水平分辨率均为30 km。所有的模拟方案均采用WSM5云物理参数化,Kain-Fritsch积云对流参数化,MYJ边界层参数化方案等相同物理参数和方案。为强化边界层内的模拟能力,所有模拟方案垂直分层均为48层,层间平均距离为200 m。其中,边界层150 m以下为8层,平均层间距为18 m。
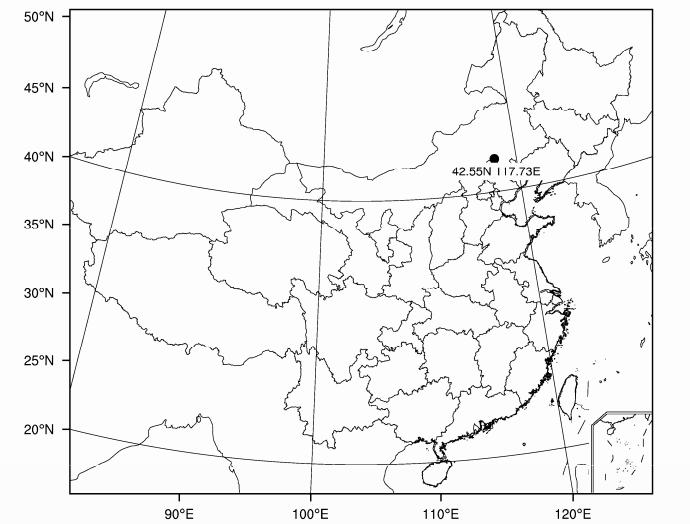 | 图 1 数值模式模拟区域Fig. 1 The simulation region of numerical model |
多资料集对比模拟试验,时间为7月2日至7月6日。该实验分别使用GFS分析资料及GFS预报资料作数值模式的初始场和边界条件,以对比分析采用两种不同资料集时模式模拟结果的差异,从而进一步研究方案1所得结论应用于实时业务预报时的可行性和科学性。GFS分析资料集以全球谱模式数值预报产品为主,经过同实时大气观测数据的资料同化订正,具有较高的空间分辨率[0.5°(纬度)×0.5°(经度)],可以认为能够准确的描述实际大气状态。
图 2为数值模拟方案1的对比结果。由图 2可知,在3日14:00之前两种方案所得结果非常相似,即可用于对比研究的有效预报时间约为36 h。为进一步精确了解两种资料集模拟结果差异,对模拟结果以8 h为单位做秩和检验,检验结果见表 3。表中p为相等概率,越大则表示两结果越接近。H表示是否具有显著差异,0表示在显著水平为0.05时两结果间无显著差异,反之,1表示在显著水平为0.05时两结果间存在显著差异。由表中数据可知,两种模拟结果直至第40 h在统计上都可认为无显著差别。因此,采用GFS分析资料作为数值模式的初始场和边界条件,来研究预报时限40 h以内的风速数值模拟统计规律并将此规律应用于优化实际业务预报结果是可行的。
 | 图 2 两种资料集模拟结果对比分析 Fig. 2 The comparing analysis of simulation results with two kind datasets |
| 表 3 秩和检验结果 Table 3 The results of rank-sum test |
实时数值气象预报模拟试验,时间为8月21日至9月2日。采用GFS全球谱模式实时数值预报产品,并通过实时风速数值模拟以检验WRF模式在实际风速预报应用中的性能。图 3为数值模拟方案2中K01号风机的对比结果,由图可知WRF模式在实际风速预报应用中有较好的效果。
 | 图 3 中尺度气象模式在实际风速预报中的应用Fig. 3 The application of mesoscale meteorological model in real wind speed forecasting |
高水平分辨率数值模拟试验,时间为观测资料质量较好的4月9日至4月12日。采用GFS分析资料作为数值模式的初始场和边界条件,空间三重嵌套模拟方案对风电场区域进行短期高分辨率模拟,以检验不同空间水平分辨率下数值模式对边界层风速的预报能力。嵌套分辨率分别为30 km、15 km、5 km。图 4为数值模拟方案3的对比结果,由图可知空间三重嵌套模拟结果非常相似,这和张宇等(2010)的研究结论是一致的。
 | 图 4 空间三重嵌套模拟结果对比分析 Fig. 4 The comparing analysis of spatial triple nested simulation results |
历史观测对比模拟试验,时间为4月1日至7月31日。采用GFS分析资料作为数值模式的初始场和边界条件,通过对风电场风速较长时间的数值模拟,并同历史观测资料进行对比以得出数值模式同观测风速差异的统计规律。2.2.4.1 数据的采样与收集
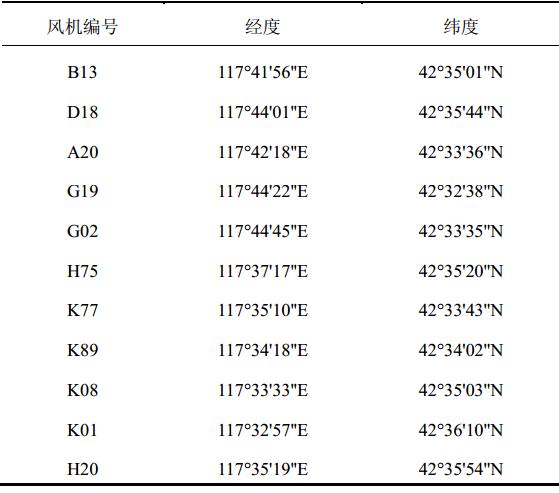
本方案所采用的风速历史数据来源于承德市红松风电场11个风机上的测风仪。采用的这11个风机上的数据,采样周期均为10 min。 采样时间始于2010年4月1日08:00,终于2010年8月2日07:50。现将这11个风机的经度以及纬度列表如表 4。
| 表 4 承德市风电场11个风机的经纬度 Table 4 The latitude and longitude of eleven aero-generators in Chengde wind farm |
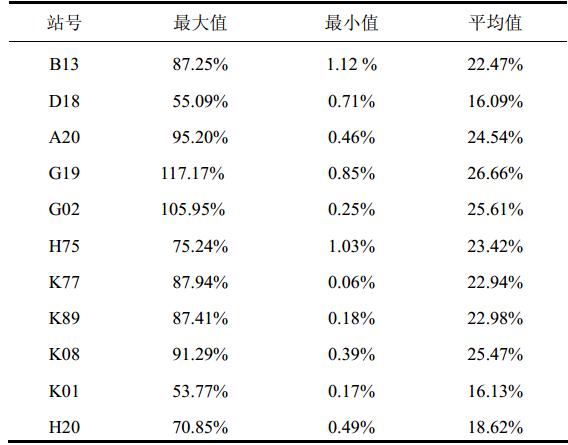
利用WRF模式预测了2010年4月1日到2010年7月31日的风速数据,其中预测时间间隔为10 min。每次预测3 d的风速数据。由于观测数据中存在大量的缺测,我们对数据进行了拼接,剔除了观测数据少于90点的观测资料(每日的观测数据应为144个)。计算了11个风机的首日预测值与对应观测风速值之间的月平均、周平均和日平均误差(表 5至表 7)。
| 表 5 月平均模式预测误差 Table 5 The monthly average forecasting error |
| 表 6 周平均模式预测误差 Table 6 The weekly average forecasting error |
| 表 7 日平均模式预测误差 Table 7 The daily average forecasting error |
从以上11 个风机的统计数据可以得出,日平均误差的均值为20.63%,周平均误差的均值为18.43%,月平均误差的均值为20.63%。对11个风机总体进行统计,日平均误差小于20%的天数占到总数的56.83%,大于50%的占到10.05%。周平均误差小于20%的周数占到总数的44.83%,大于20%的周数占到总数的为55.17%。
以B13风机为例,其中日平均误差小于10%的天数为18 d,占到总数的31.58%,平均误差在10%~20%的天数占到总数的29.82%,平均误差在20%~50%的天数占到总数的29.83%,平均误差大于50%的天数占到总数的8.77%。结果表明,WRF模式对于时间间隔为10 min的风速预测,具有较好的预报能力。2.2.4.3 预测效果
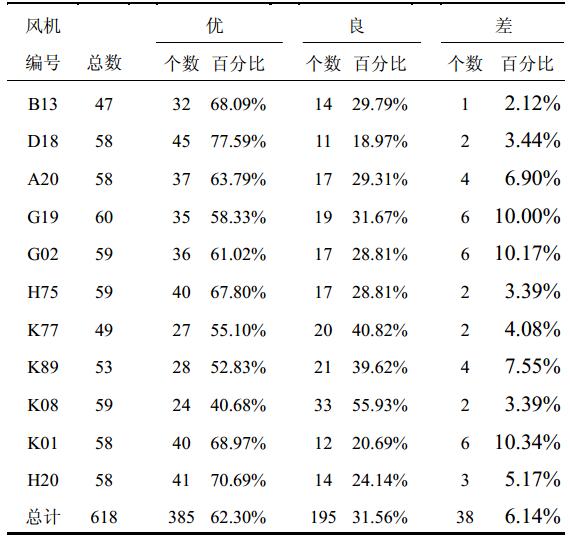
将模式方法用于风速预测研究,并将预测值与观测值进行对比。模式预测的风速值与观测风速值之间拟合优度性分为3个等级:优、良、差,详细情况如表 8所示。
| 表 8 模式预测风速值与观测风速值之间拟合优度等级评判表 Table 8 The fitting goodness degree judging table of wind speed value of model forecasting and observation |
从表 8可以看出,除了K08以外,其他10个风机均有50%以上的拟合优度占优,而除了G02和K01两个风机外,拟合优度中等级为差的所占比例均在10%以下(不包括10%)。此外,上表最后一行显示,这11个风机可用于对比的组中,62.30%的拟合性能属优,其余的占31.56%。
我们对预测结果进行了大体的分类,分为优、良、差3种。优,即3 d的预测结果与真实数据的趋势大致相符;良,即有1 d的预测结果与趋势不符;差,即有2 d的预测结果与趋势不符。现从每个等级中选取两个附图(图 5),从图 5可以看出,无论是优、良、差哪个等级,第1天的模式预测效果都是比较理想的,与第1天相比,第2、3天的预测效果均有所下降。
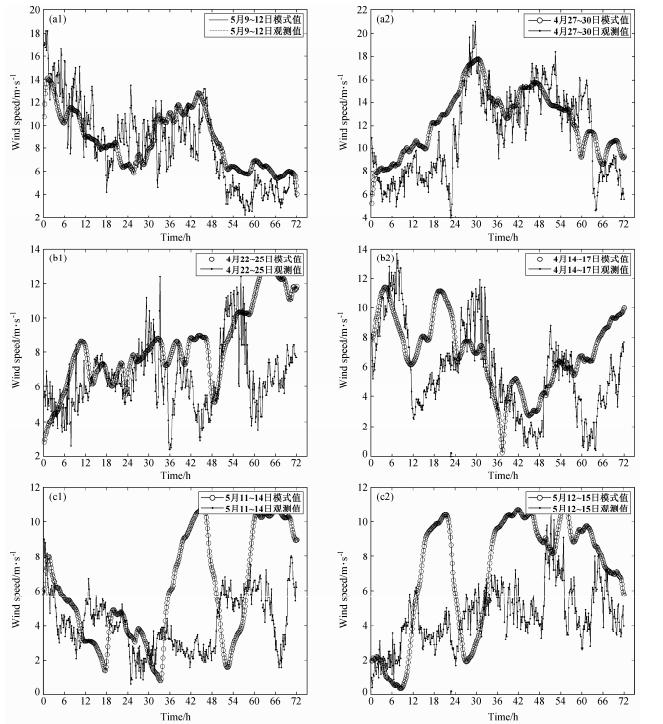 | 图 5(a1、a2)优、(b1、b2)良、(c1、c2)差性能图例 Fig. 5 The three cases for(a1,a2)excellent,(b1,b2)good,(c1,c2)bad performance |
尽管上述模式预测方法取得了较理想的结果,但是某些时段的模式预测值与观测值之间仍有很大的偏差。通过假设检验发现,这种偏差具有一定的统计规律。因此下面将采用智能优化技术对这种偏离进行校正与拟合。2.3 智能优化技术对模式误差的校正方案
针对WRF模式的误差特点,探讨一种新的修正模式误差的方法。即应用关联规则方法,挖掘出模式风速模拟数据与气压、温度、湿度及较大风速预测误差之间的关联关系,进而用统计及智能优化方法修正模式误差。
利用WRF模式,对承德红松风电场的风速进行预报,预报时效为72 h,时间分辨率为10 min。再利用智能优化方法对模拟结果进行订正。为了验证方法的普适性,我们将对与承德风能变化情况相似的内蒙古风电场的风速进行预报和订正。2.3.1 峰的定义
智能优化技术主要是针对峰提出的,首先给出峰的定义。峰的定义:类似于图 6中第213个数据到第322个数据之间的部分。
 | 图 6 峰的示意图Fig. 6 The schematic diagram of peak |
通过以下4个指标来判断是否应对于现存的峰进行智能优化:(1)爬坡率:峰的左端点A到顶点B之间的所有相邻点的斜率的平均;(2)下坡率:峰的顶点B到右端点C之间的所有相邻点的斜率的平均;(3)宽度:峰所包含的观测值个数;(4)高度:峰的最大值与最小值的垂直差。
通过对大量已有的观测数据及其相应的模式数据的统计分析及假设检验,我们发现对于满足表 9的模式数据的峰需要进行智能优化。
| 表 9 需要智能优化的峰的条件 Table 9 The condition of peak needing intelligent optimization |
为了研讨智能优化技术的有效性,我们拟定利用支持向量机或神经网络技术对峰进行识别与分类。2.3.2 用关联规则算法挖掘温度、湿度、气压与风速之间关系2.3.2.1 过滤WRF模式模拟序列
将WRF模式预报的第k个72 h模拟风速序列记为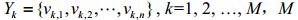 为预报总天数,vk,i是序列中第i时刻的风速值。利用盒式过滤器对模拟序列进行过滤。积分过滤过程可用如下公式表示:
为预报总天数,vk,i是序列中第i时刻的风速值。利用盒式过滤器对模拟序列进行过滤。积分过滤过程可用如下公式表示:

其中,过滤函数可写为:

其中,θ是台阶函数,
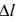 是积分过滤边长。对应的离散形式为:
是积分过滤边长。对应的离散形式为:
当
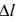 为奇数时,
为奇数时, ,其中,fix(n)的意义是取小于n的整数。
,其中,fix(n)的意义是取小于n的整数。以2010年5月22日08:00至2010年5月25日08:00 的模拟风速序列为例。令过滤器的长度 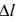 =25,25对应的时间长度为4 h。经过滤波,小尺度运动已经过滤掉了,只剩下大于尺度
=25,25对应的时间长度为4 h。经过滤波,小尺度运动已经过滤掉了,只剩下大于尺度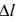 的可解尺度运动。休斯提出在可解尺度中可以进一步分解为可解大尺度和可解小尺度。我们对序列进行4次过滤。由于序列两端(小于
的可解尺度运动。休斯提出在可解尺度中可以进一步分解为可解大尺度和可解小尺度。我们对序列进行4次过滤。由于序列两端(小于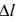 /2的序列)未过滤,取3为滤波边长,对两段序列进行4次过滤。过滤后的序列记为
/2的序列)未过滤,取3为滤波边长,对两段序列进行4次过滤。过滤后的序列记为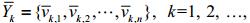 M。得到的过滤结果如图 7。
M。得到的过滤结果如图 7。
 | 图 7 2010年5月22日08:00至2010年5月25日08:00风速序列过滤前后的比较Fig. 7 The comparison of wind speed sequences before and after filter from 0800 LST 22 May to 0800 LST 25 May 2010 |
加速度:风速的变化量与对应的时间的比值。公式如下:

这里取
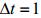 ,则加速度公式简化为
,则加速度公式简化为 。函数的导数为零的点称为函数的驻点,在驻点处的单调性会改变,通过驻点可以划分出函数的单调区间。由过滤后的风速模拟序列
。函数的导数为零的点称为函数的驻点,在驻点处的单调性会改变,通过驻点可以划分出函数的单调区间。由过滤后的风速模拟序列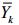 的加速度,计算出驻点位置。每72 h预报有432个数据。以2010年4月21日08:00至2010年4月24日08:00的风速预报序列为例,驻点位置如表 10。
的加速度,计算出驻点位置。每72 h预报有432个数据。以2010年4月21日08:00至2010年4月24日08:00的风速预报序列为例,驻点位置如表 10。| 表 10 序列中驻点的位置 Table 10 The position of stagnation point in sequence |
通过驻点划分函数的单调区间。由单调区间区分出不同的波形,定义从一个驻点单调递增到下一个驻点再单调递减到第3个驻点的序列为一个完整波段。分解的波段,记为,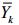 (t)(i=1,2,…,n),n为分解出的波段总数,如图 8所示,图中将一个72 h的观测序列分解为4个波段。
(t)(i=1,2,…,n),n为分解出的波段总数,如图 8所示,图中将一个72 h的观测序列分解为4个波段。
 | 图 8 2010年4月21日08:00至2010年4月24日08:00风速预报序列分解波段图Fig. 8 The resolved b and image of wind forecasting sequence from 0800 LST 21 Apr to 0800 LST 24 Apr 2010 |
计算各风速预报序列分解波段的预测误差。之后用多维关联规则中的Apriori算法,挖掘较大的分解波段误差与其对应的温度、湿度、气压及之间的关系。它包括两个方面:(1)找到所有支持度大于最小支持度的频集,即通过循环模式对所有频集进行过滤,略去支持度小于限定值的频集(frequent itemset)。(2)以(1)中产生的频集为基础,产生满足最小置信度的关联规则。原始的Apriori算法只适用于单层单维数据库,而风电信息系统均为多层多维结构,因此必须对Apriori算法进行改进。常用的方法是将数据立方体中的每个维看作一个谓词,这样就可以挖掘多层多维数据库的关联规则了。
2.3.2.4 评价关联规则
用支持度、置信度和增益来评价上述所建立的关联规则。其中支持度和置信度是评价关联规则是否成立所必须参考的条件,增益则属于附加条件,用于帮助去除看似合理但实际并不成立的伪关联。在使用中应尽量综合考虑3个因素(其中支持度和置信度为必需),单独以其中一个或两个进行评价都可能产生偏差。2.3.2.5 实现关联规则挖掘
运用Access2003和VBA 语言建立数据库,依据约束原则并结合Apriori算法思想,对数据库中曲线进行挖掘,探求符合实际的关联规则,根据实际情况设定min_sup(最小支持度)和min_con(最小置信度)的百分比。2.3.2.6 关联规则应用
利用上述多维关联规则所挖掘的信息以更好的确定模式预测中的参数和初始值,确保所建模型在在风速预测中具备良好的外推、内插能力。3 结论与讨论
按照风电调度以及风电厂并网的技术标准发展要求,最理想的情况是对每个风力发电机提供准确的72 h瞬时风速预报,这样可以从容调度。事实上,这一点在实际操作过程中很难实现。目前一些风电发展发达国家的业务应用24 h风速预报日平均相对误差在20%~25%(杨秀媛等,2005),我国24 h风速预报的日平均相对误差略低于国际水平。目前国内仍然缺少成熟的风电风速预报系统,这与发达国家的水平存在很大的差距。
本文提供了一种新的基于WRF模式和关联规则优化的风电厂短期风速预报方法。首先利用WRF模式,预测了承德红松风电场的风速。预报时效为72 h,时间分辨率为10 min。之后,本文针对WRF模式的误差特点,利用模式与统计及数据挖掘相结合的方法提高风电场风速预报精度。结合中国风电场的气候特征,提出一种新的修正模式误差的方法,即应用关联规则方法挖掘出模式风速模拟数据与气压、温度、湿度及较大风速预测误差之间的关联关系,进而用统计及智能优化方法修正模式误差。在模式方法与统计方法及智能优化算法相结合的基础上,提出了建立有效的适合中国风力发电场的风速预报系统方案,给出了该预报系统具体应用的案例。
| [1] | Alexiadis M C, Dokopoulos P S, Sahsamanoglou H S. 1999. Wind speed and power forecasting based on spatial correlation models [J]. IEEE Transactions on Energy Conversion, 14 (3): 836-842. |
| [2] | Barbounis T G, Theochairs J B, Alexiadis M C, et al. 2006. Long-term wind speed and power forecasting using local recurrent Neural Network Models [J]. IEEE Transactions on Energy Conversion, 21 (l): 273-284. |
| [3] | Bossanyi E A. 1985. Short-term wind prediction using Kalman filters [J]. Wind Engineering, 9 (l): 1-8. |
| [4] | Box G E P, Jenkins G M. 1976. Time Series Analysis: Forecasting and Control [M]. San Francisco: Holden-Day, 101-120. |
| [5] | Carolin M M, Fernandez E. 2007. Analysis of wind power generation and prediction using ANN: A case study [J]. Renewable Energy, 32: 814-831. |
| [6] | 雷亚洲, 王伟胜, 印永华, 等. 2002. 风电对电力系统运行的价值分析 [J]. 电网技术, 26 (5): 10-14. Lei Yazhou, Wang Weisheng, Yin Yonghua, et al. 2002. Analysis of wind power value to power system operation [J]. Power System Technology (in Chinese), 26 (5): 10-14. |
| [7] | 林海涛. 2010. 考虑气象因素的风电场风速及风电功率短期预测研究 [D]. 上海交通大学硕士学位论文, 97pp. Lin Haitao. 2010. Research on Short-Term Wind Speed and Wind Power Forecasting Considering Meteorological Factors in Wind Farm [D]. M. S. thesis (in Chinese), Shanghai Jiao Tong University, 97pp. |
| [8] | 刘永前, 韩爽, 胡永生. 2007. 风电场出力短期预报研究综述 [J]. 现代电力, 24 (5): 6-11. Liu Yongqian, Han Shuang, Hu Yongsheng. 2007. Review on short-term wind power prediction [J]. Modern Electric Power (in Chinese), 24 (5): 6-11. |
| [9] | Pinson P, Siebert N, Kariniotakis G. 2003. Forecasting of Regional Wind Generation by a Dynamic Fuzzy-Neural Networks Based Up scaling Approach [C]. Madrid: European Wind Energy Conference & Exhibition EWEC, 2003. |
| [10] | 沈桐立, 田永祥, 葛孝贞, 等. 2003. 数值天气预报 [M]. 北京: 气象出版社, 471pp. Shen Tongli, Tian Yongxiang, Ge Xiaozhen, et al. 2003. Numerical Weather Prediction (in Chinese) [M]. Beijing: China Meteorological Press, 471pp. |
| [11] | 孙川永, 陶树旺, 罗勇等. 2009. 高分辨率中尺度数值模式在风电场风速预报中的应用 [J]. 太阳能学报, 30 (8): 1097-1099. Sun Chuanyong, Tao Shuwang, Luo Yong, et al. 2009. The application of high resolution mesoscale model in wind speed forecatting in wind farm [J]. Acta Energiae Solaris Sinica (in Chinese), 30 (8): 1097-1099. |
| [12] | 王晓兰, 李辉. 2010. 风电场输出功率年度预测中有效风速预测研究 [J]. 中国电机工程学报, 30 (8): 117-122. Wang Xiaolan, Li Hui. 2010. Effective wind speed forecasting in annual prediction of output power for wind farm [J]. Proceedings of the Chinese Society for Electrical Engineering (in Chinese), 30 (8): 117-122. |
| [13] | 王永熙, 张源. 2002. 风力发电 [M]. 北京: 中国电力出版社, 34-35. Wang Yongxi, Zhang Yuan. 2002. Wind Power (in Chinese) [M]. Beijing: China Electric Press, 34-35. |
| [14] | 杨秀媛, 肖洋, 陈树勇. 2005. 风电场风速和发电功率预测研究 [J]. 中国电机工程学报, 25 (11): 1-5. Yang Xiuyuan, Xiao yang, Chen Shuyong. 2005. Wind speed and generated power forecasting in wind farm [J]. Proceedings of the Chinese Society for Electrical Engineering (in Chinese), 25 (11): 1-5. |
| [15] | 张宇, 郭振海, 张文煜, 等. 2010. 中尺度模式不同分辨率下大气多尺度特征模拟能力分析 [J]. 大气科学, 34 (3): 653-660. Zhang Yu, Guo Zhenhai, Zhang Wenyu, et al. 2010. Analysis of mesoscale numerical model’s ability of atmospheric multi-scale characteristics simulation in variety resolution [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 34 (3): 653-660. |
| [16] | 郑飞. 2007. ENSO集合预报研究 [D]. 中国科学院大气物理研究所博士学位论文, 174pp. Zheng Fei. 2007. Research on ENSO Ensemble Predictions [D]. Ph. D thesis (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Sciences, 174pp. |
 2012, Vol.17
2012, Vol.17