2 南京信息工程大学气象灾害预报预警与评估协同创新中心, 南京 210044;
3 江苏省大数据分析技术重点实验室, 南京 210044
2 Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044;
3 Jiangsu Key Laboratory of Big Data Analysis Technology, Nanjing 210044
气象观测资料的质量控制是气象资料服务与应用的基础,对数值天气预报以及气候研究具有重要的作用。地面气象站在数据采集过程中容易受到粗大误差、随机误差和系统性偏差的干扰,而质量控制的主要任务和目的是从众多的观测资料中识别出粗大误差和较大的随机误差(陶士伟等,2009)。为了保障地面观测资料有效真实地反应地表信息,对地面观测资料进行质量控制是必不可少且至关重要的(Alexander et al.,2006)。
传统的质量控制方法已经被广泛地应用于地面气象观测资料控制,包括极值范围检查、内部一致性检查、时间一致性检查、空间一致性检查等,Feng et al.(2004)对其作了详细描述。地面气象观测资料的质量控制分为两种情况,一种是单站质量控制(叶小岭等,2014),另一种则是多站质量控制。对于多站质量控制,国内外学者提出了很多种方法,如空间回归法(Hubbard and You,2005)、反距离权重法(Barnes,1964; Wade,1987)、内插法(Dodson and Marks,1997)等。多站质量控制方法是充分利用与目标站邻近的多个台站同时刻的观测资料,对目标站观测资料进行质量控制的方法。熊安元(2003)介绍了北欧国家对实时和非实时气象资料进行质量控制的流程以及所采用的方法和技术等。Eischeid et al.(1995,2000)介绍了统计学方法中的多种回归方法来寻求无偏估计。尹嫦姣等(2010)提出了空间差值法,并给出空间差值法优于空间回归法的结论。王海军和刘莹(2012)提出了基于线性回归数据估计方法的质量检查方法,具有第一类错误率较低以及时间和空间一致性的特点,有较高的错误数据检测性能。Xu et al.(2014)提出了基于空间回归测试的概率时空法(probabilistic spatiotemporal approach based on a spatial regression test,SRT-PS),该方法利用概率时空方法对气温资料的不确定性进行估计,并指出此方法优于空间回归法,但由于其是基于SRT方法的,会受限于台站密度及气温随机波动的影响。
基于以上研究,本文提出的方法先在空间维度上利用反距离加权(inverse distance weighting,IDW)方法通过邻站对目标站的值进行估计,再在时间维度上对目标站的观测值和IDW的估计值进行回归,通过拟合优度(确定系数,coefficient of determination,R-square)和均方根误差(root-mean- square error,RMSE,记为RMSE)两项指标确定模型阶数,从而形成了一种空间质量控制方法——AI方法。
2 资料选择本文涉及的地面气象资料为江苏省2007年地面逐时气温资料,数据是经过单站质量控制后的基本站数据,可信度较高;选取连云港58044站、徐州58027站、南京58238站、无锡58353站为中心观测站,90 km为半径的区域范围内的观测站作为邻站,各中心站邻站数目如表 1所示。为了检验所提出的方法的可行性,本文采用内布拉加斯大学Hubbard et al.(2005)提出的人为误差插入法,即在被检数据中随机选取3%的数据插入错误值(Hubbard et al.,2007):
| ${K_x} = {s_x}{p_x}$ | (1) |
| 表 1 90 km 范围内 4 个地区的邻站数目 Table 1 The numbers of neighboring stations for the four regions within a 90-km range |
其中,$K$为插入错误值的大小,s为目标站的地面逐时气温观测值的标准差,x为错误值插入的位置,p为服从区间[-3.5,3.5],且均值为0的均匀分布的随机数。
3 方法 3.1 自回归模型自回归(AR)模型预测是根据历史时间序列 数据构建回归方程达到对未知数据进行预测的目的。AR模型一般形式可表示为
| $\tilde y(t)= \sum\limits_{i = 1}^p {{\beta _i}y(t - i)+ \varepsilon(t)} $ | (2) |
其中,$\tilde y(t)$为AR方法得到的t时刻的预测变量,${\beta _i}$为回归系数,p为模型阶数,y(t−i)为t时刻观测值y(t)的i阶滞后项,$\varepsilon(t)$为模型的随机误差。
3.2 反距离加权模型IDW模型是一种通过邻站观测值对目标站的值进行距离权重估计的一种多站质量控制方法:
| $\hat y\left(t \right)= \frac{{\sum\limits_{i = 1}^n {{w_i}{y_i}\left(t \right)} }}{{\sum\limits_{i = 1}^n {{w_i}} }}$ | (3) |
其中,$\hat y(t)$为由IDW方法得到的t时刻的预测变量,${y_i}(t)$为第$i$个邻站t时刻的观测值,本文中权重函数${w_i}$是第$i$个邻站距目标站距离${d_i}$的倒数,即${w_i} = {d_i}^{ - 1}$。
3.3 AI方法本文在基于自回归模型与反距离加权模型的基础上提出了一种新的质量控制方法(AI方法),该方法兼顾了时间维度和空间维度两个方面对气象数据进行质量控制:
| ${y^*}(t)= \sum\limits_{i = 1}^p {{\beta _i}y(t - i)+ \alpha \hat y(t)+ \varepsilon(t)} $ | (4) |
其中,${y^*}(t)$是由AI方法得到的t时刻的预测变量,$\alpha $为回归系数。
模型阶数的选择直接影响着AI方法的精度,本文采用R-square和RMSE两个指标来选取适合本文的最佳模型阶数,仿真结果如图 1所示。图 1a中R-square在$p = 2$处达到一个较大稳定值;图 1b中RMSE在$p = 2$处跳跃至一个较小值并随后又缓慢变大,直至$p = 14$时开始变小,在$p = 17$时达到稳定。鉴于此,综合考虑R-square和RMSE,本文选择$p = 2$作为模型阶数(R-square值为0.97,RMSE值为0.08)。公式(4)可简化为:
| ${y^*}(t)= \sum\limits_{i = 1}^2 {{\beta _i}y(t - i)+ \alpha \hat y(t)+ \varepsilon(t)} $ | (5) |
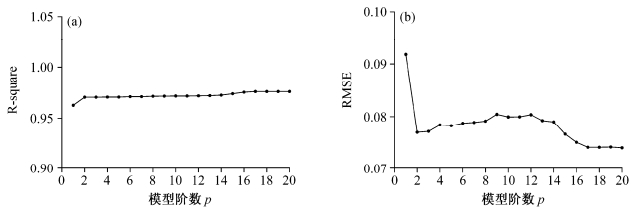 | 图 1 AI 方法在不同模型阶数 p 下的(a) R-square 值和(b) RMSE 值 Fig. 1 Values of (a) coefficient of determination (R-square) and (b) RMSE in different orders of spatial quality control method AI |
运用AI方法对各个目标站2007年的地面逐时气温进行质量控制,若预测值满足公式
| $\left| {{y_{{\rm{obs}}}} - {y_{{\rm{est}}}}} \right| \le f \cdot \delta $ | (6) |
(其中,${y_{{\rm{obs}}}}$为目标站的实际观测值,${y_{{\rm{est}}}}$为目标站的预测值,$\delta $为目标站观测值与预测值间的标准误差,$f$为质量控制参数)则认为数据可信,反之则标记为存疑数据(刘小宁等,2006)。
3.4 评价指标Nash-Sutcliffe模型系数(Nash-Sutcliffe model efficiency Coefficient,NSC,记为NSC)(Nash and Sutcliffe,1970)是用来作为实际观测值和预测值之间拟合程度的度量,其表示形式如下:
| ${N_{{\rm{SC}}}} = \frac{{\sum\limits_{i = 1}^n {({y_{{\rm{obs}}}} - \tilde y} {)^2} - \sum\limits_{i = 1}^n {({y_{{\rm{est}}}} - {y_{{\rm{obs}}}}} {)^2}}}{{\sum\limits_{i = 1}^n {({y_{{\rm{obs}}}} - \tilde y} {)^2}}}$ | (7) |
其中$\tilde y$是目标站n个样本的算术平均值。NSC的取值范围为$(- \infty,1)$,NSC越小,则目标站的实际观测值与预测值间的偏差越大,若NSC的值为负,则意味着${y_{{\rm{est}}}}$失去了其有效性。
平均绝对误差(mean absolute error,MAE,记为MAE)克服了平均误差的缺陷,能比较准确地反映预测误差的大小:
| ${M_{{\rm{AE}}}} = \frac{1}{n} \cdot \sum\limits_{i = 1}^n {\left| {{y_{{\rm{est}}}} - {y_{{\rm{obs}}}}} \right|} $ | (8) |
RMSE又叫标准误差,它对一组测量中的特大或特小误差反映非常敏感,能够很好地反映出测量的精密度:
| ${R_{{\rm{MSE}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left({{y_{{\rm{obs}}}} - {y_{{\rm{est}}}}} \right)}^2}} }}{n}} $ | (9) |
为了检验AI质量控制方法的有效性及实际控制效果,利用AI质量控制方法、SRT及IDW质量控制方法对江苏省4市地面逐时气温观测数据进行检查,各站年平均检错率如图 2所示。从图 2中可以看出AI质量控制方法在南京站、连云港站、无锡站、徐州站的平均错误检出率均高于SRT和IDW质量控制方法的平均错误检出率,SRT方法的平均检错率高于IDW方法的平均检错率,表明AI的质量控制效果优于SRT和IDW的质量控制效果,能够有效地检验出人为误差,且SRT的质量控制效果优于IDW的质量控制效果。从图 2中还可以看到,不同地区平均错误检出率差异较大,这主要是受地形和观测站分布情况影响。南京处于中纬度地区,且多低山丘陵区域,地貌形态多样;连云港地处山东中南部丘陵与淮北平原的结合部,境内平原、海洋、高山齐观,河湖、丘陵、滩涂俱备;无锡受太湖水体和宜兴南部丘陵山区复杂地形的影响,局部地区小气候条件多样,足够复杂,台站分布密集;徐州以平原为主,其台站分布在东西方向上,台站分布稀疏。AI方法、SRT方法及IDW方法均受到地形和台站分布情况的影响,但从图 2中可以看出AI方法相对于SRT和IDW方法具有更强的适应性。
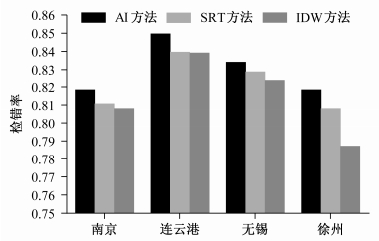 | 图 2 AI、 SRT 及 IDW 方法在不同地区对人为误差的检验结果 Fig. 2 Comparisons of AI, SRT, and inverse distance weighting (IDW) test results to human error in different regions |
图 3分别从3项指标(MAE、RMSE、NSC)来评价AI、SRT及IDW的质量控制效果(以无锡为例),从图 3中可以看出3种方法具有相同的变化趋势,但AI方法的3项性能指标均明显优于SRT和IDW方法,具有更好的表现效果。SRT方法的3项性能指标除了在1月、2月、12月低于IDW方法外,其在绝大多数月份均优于IDW方法,这3个月出现的不一致性主要在于观测数据概率分布的影响。
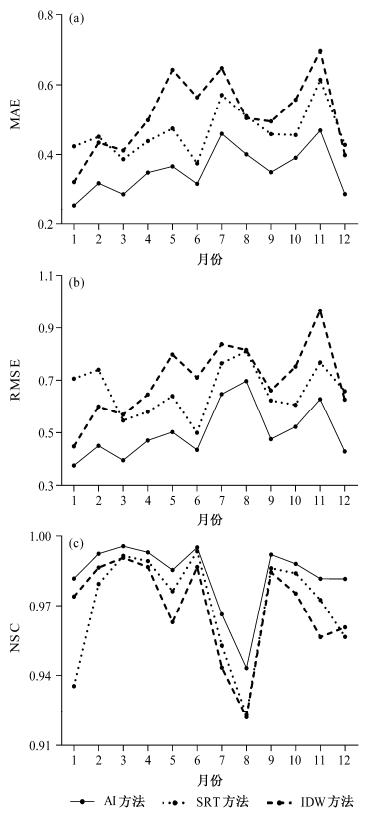 | 图 3 AI、 SRT 及 IDW 方法的 3 项性能指标在不同月份对比(以无锡为例) Fig. 3 Performance index comparisons of the AI, SRT, and IDW methods in different months (take Wuxi as an example) |
为了进一步比较AI、SRT、IDW方法在不同地区的质量控制效果,分别考察3种方法对江苏省4市2007年地面逐时气温资料的质量控制效果。如图 4所示,AI方法在4市的各项性能指标均优于SRT和IDW方法,在连云港和徐州表现尤为突出。这主要是因为连云港和徐州两市相对于南京和无锡台站数量不足且分布稀疏,无锡、南京的地形相对于连云港、徐州要稍微复杂,不利于观测资料的有效控制,但密集的台站分布弥补了地形的不足,因此在图 4中可以看到3种方法的性能指标在无锡、南京两市的差距不是很大;另一方面,AI方法的性能指标曲线相对于SRT和IDW方法的性能指标曲线变化平缓,SRT和IDW方法的性能指标曲线表现出较大的波动性,说明SRT和IDW方法相对AI方法而言更容易受到地形复杂程度及台 站密度的影响,因此AI方法的表现具有稳定性 高,适应性强的特点;另外,SRT方法在徐州地区的表现逊色于IDW方法,说明SRT方法优于IDW方法并不是绝对的,应该考虑到台站密度等的影响。
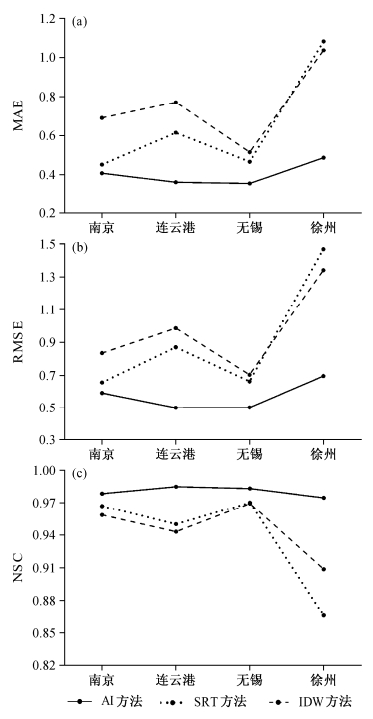 | 图 4 AI、 SRT 及 IDW 方法的 3 项性能指标在不同地区的对比图 Fig. 4 Performance index comparisons of the AI, SRT, and IDW methods in different regions |
以上试验及分析都是AI方法针对逐时或季节尺度上气温资料的质量控制,为了判别AI方法对长期气候序列中存在的质量问题的识别能力,分别用IDW、SRT和AI方法对4市2007年全年气温数据进行质量控制。如表 2所示,4种方法在4市的检错率都在70%上下浮动,且3种方法无论是对同一城市还是对不同城市,它们的检错率大小相差不大,所以AI方法对长期气候序列中存在的质量问题有识别能力,但是相对于SRT和IDW方法体现不出明显的优越性。
| 表 2 2007 年 AI、 SRT 及 IDW 方法对 4 个城市气温观测值的检错率 Table 2 Ratio comparison among the AI, SRT, and IDW methods for temperature observations in 2007 |
为了判别不同的f取值对检验效果的影响,本文运用AI质量控制法对南京站、连云港站、无锡站、徐州站2007年地面逐时气温资料进行质量控制检验,在保证对原观测资料添加人为误差保持不变的情况下,分别令f等于0.5、1、1.5、2、2.5、3、3.5,表 3为不同f值情况下AI方法的年平均检错率。从表 3中可以看出,错误检出率随着f的增大而减小;当f=0.5时,每个台站的年平均检出率都超过了0.8,表明AI方法对错误数据比较敏感;随着f的逐渐变大,错误检出率大幅度降低;当f=3.5或大于3.5时,无法检验出错误数据。
| 表 3 台站不同 f 条件下的检出率 Table 3 Human error detection rate for each station under different values of f |
在质量控制的统计检验中,当检验一个假设时会出现两种类型的错误:1)如果数据正确而被拒绝,则产生“第一类错误”,即“把真当假”;2)在数据是错误时而被接受,产生“第二类错误”,即“以假充真”。对质量控制方法来说,需要在控制第一类错误概率的前提下,尽量使第二类错误的概率达到最小(屠其璞等,1984)。图 5是运用AI方法所得的第一类错误概率和第二类错误概率随f值变化的折线图。从图 5中可以看出第一类错误的概率随着f的增大而减小;相反,第二类错误的概率随着f的增大而增大。
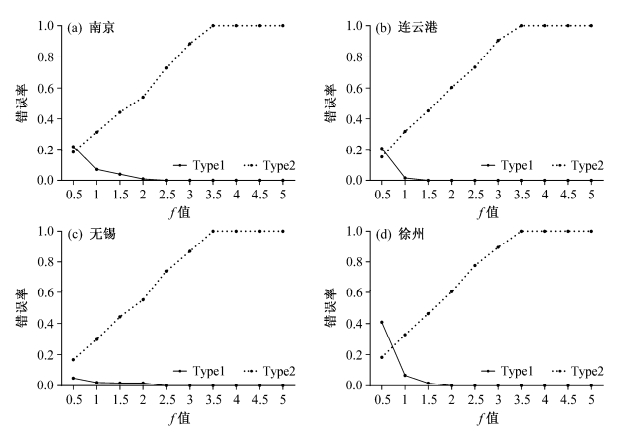 | 图 5 各台站不同 f 条件下第一类和第二类错误率 Fig. 5 Mistake rates of type 1 and type 2 errors for different stations under different values of f |
综合考虑表 3和图 5的数据与曲线,f与错误检出率存在极大的相关关系,但由于错误检出率受到样本随机抽样和插入错误值的大小的影响,我们应该根据具体要求选择合适的f值。若对数据要求较高,则f应取小一些;若要尽可能保留所有可用数据,则f应取大一些。
5 结论本文提出了一种新的质量控制方法AI方法对2007年地面逐时气温资料中的存疑数据进行检验,利用3项性能指标MAE、RMSE、NSC来评估其性能,并与IDW方法进行比较,试验表明AI方法具有更好的稳定性和适应性,能够有效地检测出地面气象观测数据中的存疑数据。通过不同的试验可以得到以下结论:
(1)总体来看,AI质量控制方法相对于SRT和IDW具有较好的质量控制效果,能够有效地标记出存疑数据。这是因为SRT方法是根据目标站与邻站的均方根误差来确定权重的,IDW方法是根据目标站与邻站的距离来确定权重的,受地理环境和台站分布密度的影响较大。而在AI方法中,各种因素对预测目标的影响是通过它们在时间维度和空间维度两个方面来体现的。
(2)AI方法在不同地区质量控制效果的性能指标曲线平缓,表明 AI方法具有稳定性高、适应性强的特点。
(3)从以上分析可以看出,AI质量控制方法比较适合用在平原或丘陵地带,而对地形复杂地区台站的数据质量控制存在局限性。针对这一点在今后的研究中我们可以在此方法的基础上将各个邻站的经纬度、海拔高度、建筑物的影响因子等作为解释变量考虑在内,对方法做适当的调整提出新的质量控制方法,从而尽可能地改善因地形复杂这一因素对质量控制的影响程度,提高方法的有效性。
(4)AI方法适合于逐时或季节尺度上气温资料的质量检验和控制,对长期气候序列中存在的质量问题也有识别能力,但是相对于SRT和IDW方法体现不出明显的优越性。
以上只是新方法在地面气温观测数据的初步研究,工作尚不全面,对于该方法在其它气象数据控制领域的应用还有待深入研究。
| [1] | Alexander L V, Zhang X B, Peterson T C, et al. 2006. Global observed changes in daily climate extremes of temperature and precipitation[J]. J. Geophys. Res., 111 (D5):D05109, doi:10.1029/2005JD006290. |
| [2] | Barnes S L.1964. A technique for maximizing details in numerical weather map analysis[J]. J. Appl. Meteor., 3(4):396-409, doi:10.1175/1520-0450(1964)003<0396:ATFMDI>2.0.CO;2. |
| [3] | Dodson R, Marks D. 1997. Daily air temperature interpolated at high spatial resolution over a large mountains region[J]. Climatic Research, 8 (1):1-20, doi:10.3354/cr008001. |
| [4] | Eischeid J K, Baker C B, Karl T R, et al. 1995. The quality control of long-term climatological data using objective data analysis[J]. J. Appl. Meteor., 34(12):2787-2795, doi:10.1175/1520-0450(1995)034<2787:TQCOLT>2.0.CO;2. |
| [5] | Eischeid J K, Pasteris P A, Diaz H F, et al. 2000. Creating a serially complete, national daily time series of temperature and precipitation for the western United States[J]. J. Appl. Meteor., 39 (9):1580-1591, doi:10.1175/1520-0450(2000)039<1580:CASCND>2.0.CO;2. |
| [6] | Feng S, Hu Q, Qian W H. 2004. Quality control of daily meteorological data in China, 1951-2000:A new dataset[J]. International Journal of Climatology, 24 (7):853-870, doi:10.1002/joc.1047. |
| [7] | Hubbard K G, You J S. 2005. Sensitivity analysis of quality assurance using the spatial regression approach-A case study of the maximum/minimum air temperature[J]. J. Atmos. Oceanic Technol., 22 (10):1520-1530, doi:10.1175/JTECH1790.1. |
| [8] | Hubbard K G, Goddard S, Sorensen W D, et al. 2005. Performance of quality assurance procedures for an applied climate information system[J]. J. Atmos. Oceanic Technol., 22 (1):105-112, doi:10.1175/JTECH-1657.1. |
| [9] | Hubbard K G, Guttman N B, You J S, et al. 2007. An improved QC process for temperature in the daily cooperative weather observations[J]. J. Atmos. Oceanic Technol., 24 (2):206-213, doi:10.1175/JTECH1963.1. |
| [10] | 刘小宁, 鞠晓慧, 范邵华. 2006. 空间回归检验方法在气象资料质量检验中的应用[J]. 应用气象学报, 17 (1):37-43. Liu Xiaoning, JuXiaohui, Fan Shaohua. 2006. A research on the applicability of spatial regression test in meteorological datasets[J]. Journal of Applied Meteorological Science (in Chinese), 17 (1):37-43, doi:10.3969/j.issn.1001-7313.2006.01.005. |
| [11] | Nash J E, Sutcliffe J V. 1970. River flow forecasting through conceptual models part I-A discussion of principles[J]. J. Hydrol., 10(3):282-290, doi:10.1016/0022-1694(70)90255-6. |
| [12] | 陶士伟, 仲跻芹, 徐枝芳, 等. 2009. 地面自动站资料质量控制方案及应用[J]. 高原气象, 28(5):1202-1209. Tao Shiwei, Zhong Qiqin, Xu Zhifang, et al. 2009. Quality control schemes and its application to automatic surface weather observation system[J]. Plateau Meteorology (in Chinese), 28 (5):1202-1209. |
| [13] | 屠其璞, 王俊德, 丁裕国, 等. 1984. 气象应用概率统计学[M]. 北京:气象出版社, 198pp. Tu Qipu, Wang Junde, Ding Yuguo, et al. 1984. Meteorological Application of Probability and Statistics (in Chinese)[M]. Beijing:China Meteorological Press, 198pp. |
| [14] | Wade C G. 1987. A quality control program for surface mesometeorological data[J]. J. Atmos. OceanicTechnol., 4(3):435-453, doi:10.1175/1520-0426(1987)004<0435:AQCPFS>2.0.CO;2. |
| [15] | 王海军, 刘莹. 2012. 综合一致性质量控制方法及其在气温中的应用[J]. 应用气象学报, 23 (1):69-76. Wang Haijun, Liu Ying. 2012. Comprehensive consistency method of data quality controlling with its application to daily temperature[J]. Journal of Applied Meteorological Science (in Chinese), 23 (1):69-76, doi:10.3969/j.issn.1001-7313. 2012. 01.008. |
| [16] | 熊安元. 2003. 北欧气象观测资料的质量控制[J]. 气象科技, 31(5):314-320. Xiong Anyuan. 2003. Quality control of meteorological observational data in Nordic countries[J]. Meteorological Science and Technology (in Chinese), 31 (5):314-320, doi:10.3969/j.issn.1671-6345. 2003.05.013. |
| [17] | Xu C D, Wang J F, Hu M G, et al. 2014. Estimation of uncertainty in temperature observations made at meteorological stations using a probabilistic spatiotemporal approach[J]. Journal of Applied Meteorology and Climatology, 53 (6):1538-1546, doi:10.1175/JAMC-D-13-0179.1. |
| [18] | 叶小岭, 周建华, 熊雄. 2014. 一种基于GEP的地面气温观测资料的质量控制方法[J]. 热带气象学报, 30(6):1196-1200. Ye Xiaoling, Zhou Jianhua, XiongXiong. 2014. A GEP-based method for quality control of surface temperature observations[J]. Journal of Tropical Meteorology (in Chinese), 30(6):1196-1200, doi:10.3969/j.issn.1004-4965.2014.06.021. |
| [19] | 尹嫦姣, 江志红, 吴息, 等. 2010. 空间差值检验方法在地面气象资料质量控制中的应用[J]. 气候与环境研究, 15(3):229-236. Ying Changjiao, Jiang Zhihong, Wu Xi, et al. 2010. A research on the application of spatial difference method in quality control of surface meteorological data[J]. Climatic and Environmental Research (in Chinese), 15(3):229-236. |
 2016, Vol. 21
2016, Vol. 21


