在全球变暖背景下,地表蒸发加剧,全球和区域水循环加剧,造成极端降水事件增多(Trenberth, 1998; Trenberth et al., 2003)。江淮流域是东亚季风降水的核心区域(Ding, 1994;胡娅敏和丁一汇,2009;梁萍等,2008),研究该地区的降水事件,对提高防灾减灾能力、制定应对气候变化的策略和措施具有重要科学意义和实际应用价值。目前,全球气候模式(global climate models,简称GCM)能够较好地模拟大尺度环流场及气候要素的平均特征(江志红等,2009;许崇海等,2010),但由于空间分辨率有限(王冀等,2008),GCM难以准确模拟区域尺度气候要素的时空变化(高学杰等,2006;郭彦和李建平,2012)。因此,弥补GCM的不足,获取较为精确的区域气候信息十分必要。
对全球模式进行降尺度是得到区域尺度精细信息较可行的方法。降尺度方法主要有动力降尺度和统计降尺度两种方法。其中统计降尺度主要利用多年观测资料建立区域气候要素与大尺度大气环流的统计关系,并用独立的观测资料检验这种关系,最后将这种关系应用到模式输出的环流中,从而预测未来的气候变化(范丽军等,2005)。相对于动力降尺度,统计降尺度所需的计算资源小,能较快运用到不同的GCM,灵活性很强(范丽军等,2007)。如贾小龙等(2010)采用典型相关分析的方法,建立了我国冬季平均降水量与东亚500 hPa高度场的统计降尺度模型。Zhu et al.(2008)利用EOF和SVD(singular value decomposition)结合的方法,建立了夏季东亚平均降水量距平和500 hPa位势高度场的统计降尺度模型。崔妍等(2010)利用典型相关分析的方法,建立了江淮流域极端降水指数和温度场、海平面气压场和比湿场的统计降尺度模型。但这些统计降尺度方法都仅考虑了月(季节)平均环流及其与相关要素的关系,由于极端降水事件的气候特征(如强度、频率的变化)与天气尺度环流型态关系密切,月以上尺度要素的降尺度无法体现上述关系,因此非常有必要建立逐日天气型态与局地降水条件分布的联系,以便提高日降水概率分布及其极端降水特征的模拟能力。
自组织映射神经网络(SOM)是一种无监督的人工神经网络模型,Kohonen于1982年提出了SOM的算法并介绍了算法的具体实现过程(Kohonen, 1982, 2000),该方法主要是基于神经网络原理反复进行自我学习、训练,可以对高维气象场变化数据进行聚类,得到各类优势环流模态(获胜神经元)及其演变(Hewitson and Crane, 2002; Radić and Clarke, 2011; Wang et al., 2015)。Hewitson and Crane(2006)将该方法引入统计降尺度研究中,通过建立环流模态及其演变与日降水量分布的联系,进行了南非逐日降水降尺度试验。后来Yin et al.(2011)将该方法应用到澳大利亚的降水模拟中,发现该方法不仅能再现观测降水的平均统计特征,还能重现极端降水,并能模拟出降水的年际变化。Ning et al.(2012a)利用该方法对美国宾夕法尼亚州13个台站的降水量进行统计建模,并将降尺度模型运用到9个CMIP3模式中,得到历史时期模式的降尺度结果。发现与全球模式的模拟结果相比,降尺度结果能够模拟出与观测更一致的降水概率分布和日、月尺度上的降水时空特征。但SOM降尺度建模在国内尚未见到相关应用。
本文利用1961~1990年ERA-40再分析数据和同期台站逐日观测降水量数据,引入SOM统计降尺度方法,建立江淮流域56个台站的夏季逐日降水的降尺度模型,并由独立样本(时期1991~2002年)的观测资料评估该模型的模拟性能。同时考察其对BCC-CSM1.1(m)模式当前气候模拟的降尺度效果,研究该方法对我国江淮流域夏季逐日降水进行降尺度的适用性,为进一步利用SOM进行极端降水的未来变化预估提供基础。
2 资料与方法 2.1 资料利用欧洲中心ERA-40逐日再分析资料(分辨率为2.5°×2.5°,时间为1961~2002年夏季6~8月)(Uppala et al., 2005)和同期中国气象局台站逐日降水量观测资料。模式选取BCC-CSM1.1(m)模式,该模式是国家气候中心研发的大气—海洋—陆面—海冰耦合的全球气候模式,水平分辨率为T106波谱截断(全球分辨率近似为1.125°(纬度)×1.12°(经度)),时间选取1986~2005年,该模式对我国东部环流和降水具有较好的模拟能力,具体可参见文献(Wang et al., 2015;陈晓晨等,2014;黄海玲等,2015)。降尺度区域为江淮流域(27.5°N~32°N, 110°E以东),图 1为该区域台站分布。

|
图 1 江淮流域56个代表台站的分布 Fig. 1 Geographic locations of the 56 representative stations over Yangtze–Huaihe River basin |
参考Hewitson and Crane(2006)、Yin et al.(2011)和Ning et al.(2012a)的研究,用于描述天气型态的要素主要有高、低层纬向风速(u)和经向风速(v)、海平面气压、温度、比湿和相对湿度。我们选取ERA-40逐日再分析数据中850 hPa相对湿度和比湿、地面温度、850 hPa~500 hPa温度直减率(由850 hPa和500 hPa温度计算得到)、850 hPa纬向风速(u)和经向风速(v)以及海平面气压7个气象要素,用于获取与逐日降水联系的天气型态。BCC-CSM1.1(m)模式中选用的要素同上,并且还使用了模式原始模拟的降水进行对比分析。
2.2 SOM降尺度方法简介SOM能够根据原始高维气象数据的拓扑关系,对样本进行自组织学习,反复调整连接输入和输出的权重系数,使系数反映样本间相互距离的关系,得到优势模态(Kohonen, 1982, 2000),该网络由输入层和竞争层组成,竞争层是由a×b个神经元组成的二维平面阵列。SOM优势模态的具体计算过程可参见Wang et al.(2015)和Chu et al.(2012)。
SOM的降尺度方法中,首先利用SOM建立天气模态与日降水分布的关系,对模拟期的环流采用投影的方式确定其对应的降水分布,进而利用Monte-Carlo方法模拟得到降水量。这里我们简述SOM降尺度方法的主要步骤,详细介绍可参见Hewitson and Crane(2006):
(1) 主要天气模态的提取。定义SOM竞争层神经元个数为4×5,将目标台站所在区域的天气分为20种类型。即对目标台站附近区域的地面温度、海平面气压、850 hPa相对湿度和比湿、850 hPa的纬向风速(u)和经向(v)风速、850 hPa~500 hPa温度直减率7个气象变量组成的逐日天气模态进行SOM训练,得到20(4×5)种主要天气模态。
(2) 建立主要天气模态与各台站降水条件概率分布的联系。
(3) 独立样本检验期天气模态的确定。根据独立样本检验期天气场与SOM最佳匹配神经元的距离最小原则(Yin et al., 2011),确定独立样本检验期逐日的主要天气模态。
(4) 降水量的随机模拟。根据(3)确定的独立样本试验期的天气模态,利用(2)中主要天气模态与台站降水量的关系,通过Monte-Carlo模拟方法(Lall and Sharma, 1996),得到各台站的逐日降水量。SOM降尺度效果与随机模拟次数有关,综合考虑各台站的模拟效果和计算时间,我们取模拟次数为500。
2.3 降水指数为进一步考察SOM降尺度方法对不同降水特征的模拟,我们选取了6个降水指数进行降尺度效果评估,降水指数分别为:降水日数(R1mm)、中雨日数(R10mm)、夏季总降水量(PRCPTOT)、日降水强度(SDII)、极端降水阈值(P95)和极端降水贡献率(R95t),具体定义如表 1所示(Frich et al., 2002; Zhang et al., 2011;陈晓晨等,2015)。
|
|
表 1 降水相关指数定义 Table 1 Definition of precipitation-related indices |
采取可靠、有效的评估指标,对统计降尺度方法的模拟效果进行评估,是进一步利用该方法进行未来预估的基础。我们分别从降水量的概率分布、空间分布和时间变化三方面考察SOM降尺度模型对江淮流域夏季逐日降水的模拟效果。
引入定量评估日降水量概率分布模拟能力的Brier评分(Brier Score,简称SBrier)指标和显著性评分(Significance Score,简称Ss)指标(Perkins et al., 2007; Fu et al., 2013),其中SBrier定义为
| ${{S}_{Brier}}={{{\sum\nolimits_{i=1}^{n}{({{P}_{mi}}-{{P}_{oi}})}}^{2}}}/{n}\;$ | (1) |
式中,n表示区间个数,Pmi和Poi分别为降尺度和观测日降水量在第i个区间的概率。SBrier指标定量表示模拟与观测概率分布函数(probability distribution function,简称PDF)不重合的部分,SBrier越接近0,模拟与观测的PDF差异越小。Ss定义为
| ${{S}_{s}}=\sum\nolimits_{i=1}^{n}{Mini({{P}_{mi}},{{P}_{oi}})}$ | (2) |
表示所有区间模拟和观测概率最小值的累加,定量表示两种PDF的重合部分。若模拟与观测的PDF重合,Ss的值为1;反之,Ss的值越小。
另外,我们也通过Q-Q图(Quantile-Quantile Plot)对比观测样本分位数与模拟样本的分位数的一致性,由此更直观评估模拟降水分布的精度。
降水的时间变率通过标准差来衡量,根据Gleckler et al.(2008)和Santer et al.(2009)的研究,引入变率指标IMV,用于描述模拟场上每一点的时间序列与该点观测时间序列的时间变率,定义为
| ${{I}_{MV}}={{\left( \frac{{{S}_{TD}}_{m}}{{{S}_{TD}}_{o}}-\frac{{{S}_{TD}}_{o}}{{{S}_{TD}}_{m}} \right)}^{2}}$ | (3) |
式中,STDm和STDo分别为SOM降尺度和观测降水量的标准差。当模拟变率为观测变率的X倍和1/X倍时,二者具有一样的IMV值。IMV等于0,表明SOM降尺度模拟时间变率等于观测时间变率;反之IMV越大,模拟时间变率的能力越差(Chen et al., 2011)。
我们还计算了相对误差百分率、空间场相关系数来评估SOM降尺度对降水量的空间分布和时间变化的模拟能力,并采用泰勒图法直观表示SOM降尺度和模式对不同降水指数空间分布的模拟能力(Taylor,2001)。
3 SOM降尺度模型的建立利用1961~1990年的ERA-40再分析数据及同期台站观测的夏季降水量数据,建立降尺度模型,1991~2002年作为独立样本检验期,将该时段的ERA-40数据代入降尺度模型,模拟得到台站的日降水量并与观测降水量对比分析,以评估SOM降尺度模型对江淮流域夏季降水的模拟效果。
3.1 SOM模态的提取按照2.2节中SOM降尺度方法步骤1,设置竞争层神经元个数20(4×5),对各降尺度目标台站附近区域7个气象变量组成的逐日天气模态进行SOM训练,得到该台站对应的20种主要天气模态。以海平面气压场为例,图 2给出建模期武汉站20种主要SOM模态对应的海平面气压场分布,其中h表示天气型的出现频率,qe(quantization error)为量化误差,表示某一模态对应样本与该模态最佳匹配神经元参照向量的平均欧氏距离,类似于聚类分析中的组内变化,表征SOM的分型质量。可以看到,主要SOM模态对应的海平面气压场出现的频率在2%~8%之间。量化误差都低于10,并且在不同神经元上分布较均匀,说明所有模态能一致地反映样本信息。图中左上角的天气型主要由高压主导,右下角为低压主导,中间为过渡类型,邻近神经元的气压分布相似,距离远的神经元气压分布差别大,表明20种主要SOM模态都能清楚地表示主要天气型对应的海平面气压场分布及其变化。
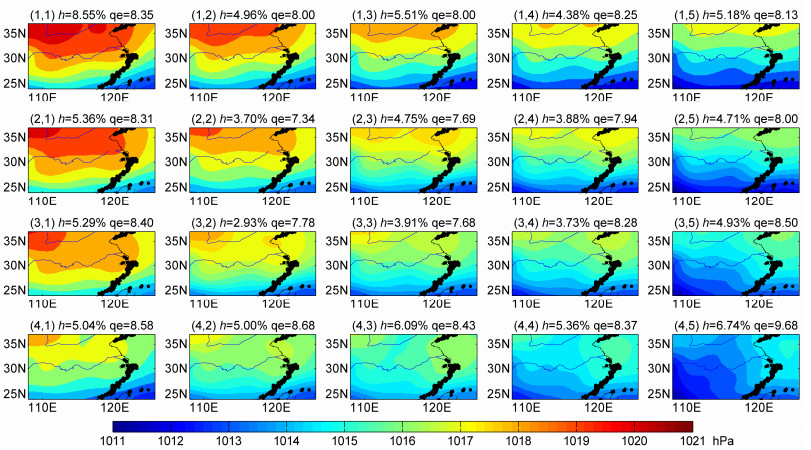
|
图 2 建模期(1961~1990年)武汉站主要天气模态的海平面气压分布(单位:hPa),h为频率,qe为平均量化误差(单位:1) Fig. 2 SLP (units: hPa) distributions corresponding to primary weather patterns at Wuhan station during the modeling period (1961–1990). 'h' denotes the frequency across the SOM (Self-Organizing Map) nodes; 'qe' represents the average quantization error (units: 1) |
根据4.1节中的主要模态,得到每种主要模态对应的降水量条件概率分布(图 3)。由图可见,相邻神经元的降水量累积概率分布(cumulative distribution function,简称CDF)类似,而距离远的神经元降水量分布差异大。联系图 2,可以发现高压主导的神经元的降水量比低压主导的神经元的降水量少,说明SOM得到的天气型与降水量的关系是合理的,不同模态能够体现不同的降水量分布特征。

|
图 3 建模期(1961~1990年)武汉站主要天气模态对应的逐日降水量(单位:mm)累积概率分布 Fig. 3 Cumulative distribution functions (CDFs) of daily precipitation (units: mm) corresponding to primary weather patterns at Wuhan station during the modeling period (1961–1990) |
日降水量概率分布曲线是对台站降水量总体特征的概括,图 4a–d为武汉、南京、合肥和杭州4个代表站的观测和SOM降尺度模拟的日降水量概率分布曲线图。由图可见,4个站模拟和观测PDF曲线都较为接近,小雨(0~9.9 mm d-1)模拟概率较观测略高。中雨(10~24.9 mm d-1)发生概率不同的台站有差别,武汉、合肥和杭州站较观测略低,而南京站则略高。对大于50 mm d-1暴雨的概率模拟都略低,4个台站SBrier近似为0并且Ss都在0.9以上。表明SOM降尺度模拟日降水量概率分布与观测非常接近,但模拟小雨的概率略偏高,暴雨的概率略偏低。
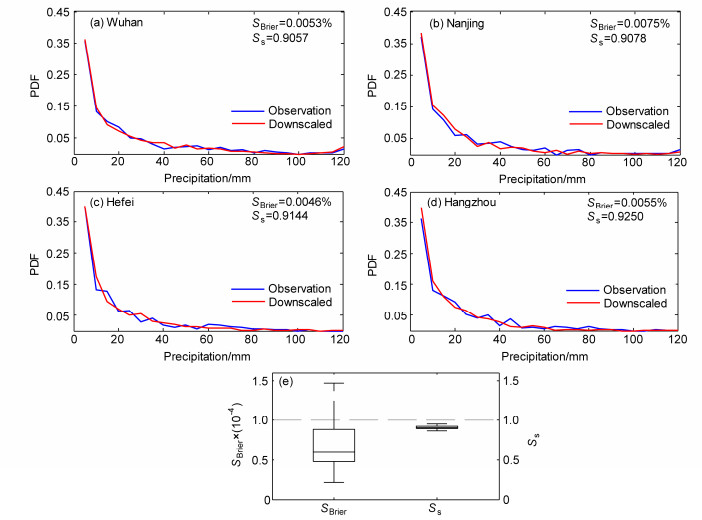
|
图 4 独立检验期(1991~2002年)夏季SOM降尺度模拟和观测的(a)武汉、(b)南京、(c)合肥、(d)杭州4个代表站雨日降水量PDF曲线和(e)SBrier(单位:10-4)、Ss指标盒须图 Fig. 4 Probability distribution function (PDF) curves for the observed and SOM downscaled simulated precipitation at stations (a) Wuhan, (b) Nanjing, (c) Hefei, (d) Hangzhou, and (e) the box plot of Brier score (SBrier) and significance score (Ss) during the independent sample test period (1991–2002) |
为进一步定量考察SOM降尺度对所有台站日降水量概率分布的模拟能力,分别计算各台站的SBrier和Ss指标,定量考察模拟与观测日降水量概率分布曲线的偏离和重合程度。图 4e为所有台站SBrier和Ss指标的盒须图。由图可见,所有台站SBrier均近似为0,Ss全部在0.8以上,最大值为0.95。表明SOM降尺度模型能很好模拟日降水量概率分布特征。
3.3.2 降水场空间分布的模拟评估为评估SOM降尺度模型对江淮流域夏季平均降水场的模拟效果,分别计算6个降水指数与观测的相对误差百分率、空间相关系数和均方根误差,如表 2所示。所有指数区域多年平均场的偏差数值都不超过11%,空间相关系数在0.7以上,并且均方根误差较小。R10mm和总降水量的模拟效果最优,偏差数值在3%以内,空间相关系数达到0.8以上,夏季总降水量的均方根误差为78.6 mm,而区域平均的夏季总降水量为613.6 mm,仅占总量的12.8%。其次为R1mm和日降水强度的模拟,SOM降尺度对区域平均R1mm模拟偏多而总降水量模拟偏少,造成日降水强度为负偏差,但偏差数值都在8%以内。降尺度对于两个极端降水指数的模拟略弱,两者平均偏差在10%左右。极端降水阈值的区域多年平均值模拟比观测偏低,而由于总降水量模拟偏少,极端降水贡献率为正偏差。
|
|
表 2 独立检验期(1991~2002年)SOM降尺度模拟与观测的各指数多年平均场的相对误差百分率、空间相关系数和均方根误差。相关系数均通过99%的信度检验 Table 2 Percentage of relative error, spatial correlation coefficient, and root mean square error between the SOM downscaled simulated and observed precipitation-related indices during the independent sample test period (1991–2002). Correlation coefficients exceed the 99% confidence level |
图 5为所有台站各指数的相对误差百分率的盒须图。由图可见,大部分台站6个指数的相对误差百分率都低于20%,R10mm和总降水量多数台站的偏差在10%以内。R1mm和R10mm多数台站模拟为正偏差,偏差中位数分别为7.1%和2.1%,负偏差主要出现在区域南部的少数台站(图略)。夏季总降水量和日降水强度多数台站模拟为负偏差,偏差中位数分别为-1.8%和-9.6%,因为多数台站总降水量模拟偏少而R1mm模拟偏多,造成日降水强度除北部少数台站外,基本为全局负偏差(图略)。对于两个极端降水指数的模拟,极端降水阈值多数台站模拟偏低,对应4.3.1节中SOM降尺度对暴雨概率的模拟偏低。极端降水贡献率多数台站的偏差在10%左右,基本为全局正偏差。
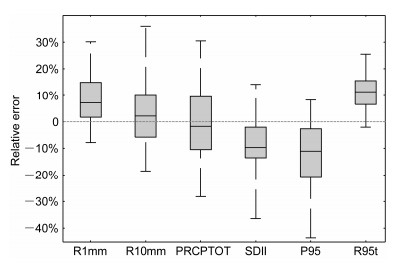
|
图 5 独立检验期(1991~2002年)SOM降尺度模拟的台站夏季多年平均降水日数(R1mm)、中雨日数(R10mm)、总降水量(PRCPTOT)、日降水强度(SDII)、极端降水阈值(P95)和极端降水贡献率(R95t)相对误差百分率的盒须图 Fig. 5 Box plot of relative errors' percentages of days of mean summer precipitation greater than 1 mm (R1mm) and 10 mm (R10mm), the total rainfall (PRCPTOT), the simple daily intensity index (SDII), the extreme daily precipitation threshold (P95), and the fraction of total precipitation due to events exceeding the 95th percentile of the climatological wet-day precipitation distribution (R95t) for the SOM downscaled simulation results compared to observed values during the independent sample test period (1991–2002) |
综上,SOM降尺度方法能够较好地模拟江淮流域夏季各降水指数多年平均场的特征,6个指数区域平均的偏差都不超过11%,并且空间相关在0.7以上。多数台站降尺度模拟的R1mm比观测偏多,偏差在20%以内,R10mm和夏季总降水量的偏差数值在10%以内,多数台站日降水强度模拟比观测略弱,偏差不超过15%。降尺度对极端降水也有一定的模拟能力,多数台站极端降水阈值模拟偏低,但偏差不超过20%,而极端降水贡献率模拟偏强,多数台站偏差不超过15%。
3.3.3 降水时间变化的模拟评估利用指数IMV可以评估SOM降尺度模型对降水时间变率的模拟能力。图 6为SOM降尺度模拟较好的多年平均夏季R1mm、R10mm、总降水量和极端降水贡献率的IMV的盒须图。由图可见,R10mm和极端降水贡献率的时间变率模拟最好,多数台站的IMV在0.5以内,中位数分别为0.21和0.17,并且不同台站IMV的离散程度小。R1mm和总降水量的IMV多数台站低于1,中位数在0.5左右。其次对于4个指数,区域东部台站的IMV比西部偏高(图略),说明对降水变率的模拟,东部台站略弱,但整体上IMV接近0,表明SOM降尺度模型可以模拟降水指数序列的时间变率。
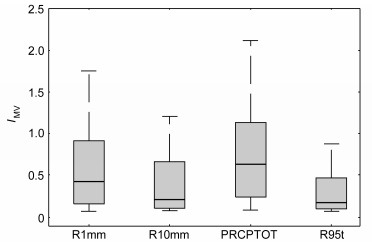
|
图 6 独立检验期(1991~2002年)SOM降尺度模拟和观测的台站夏季多年平均R1mm,R10mm,PRCPTOT和R95t的IMV指数盒须图 Fig. 6 Box plot of mean summer variability indices IMV of the SOM downscaled simulated and observed R1mm, R10mm, PRCPTOT, and R95t during the independent sample test period (1991–2002) |
进一步将SOM降尺度模型应用到BCC-CSM1.1(m)模式当前气候情景中。将BCC-CSM1.1 (m)模式中1986~2005年夏季的气象要素场代入模型,从而得到SOM降尺度模拟的降水,对比SOM降尺度前后的模拟偏差,检验SOM降尺度方法相对于BCC-CSM1.1(m)耦合模式模拟能力是否具有“附加值”,即评估SOM降尺度方法的有效性。
4.1 日降水量概率分布的模拟评估为考察SOM降尺度模型对日降水量概率分布的模拟能力,同样选取4个代表台站,武汉、南京、合肥和杭州站,给出SOM降尺度、BCC-CSM1.1(m)模拟和观测的日降水量分布Q-Q图,如图 7a–d所示。图中横坐标为观测降水量,纵坐标为降尺度和BCC-CSM1.1(m)模式模拟的降水量。由图可见,降尺度后除部分尾部的大值降水量与观测略有偏差外,四个台站的日降水量分位数与观测基本一致。当日降水量达到100 mm后,武汉站降尺度模拟的降水量略高于实际观测,偏差在20 mm以内。杭州站的日降水量在50~110 mm之间时,降尺度模拟的比观测整体偏低,偏差在10 mm以内。而南京和合肥站除最大日降水量降尺度模拟比观测偏小外,其余均与观测一致,最大日降水量的偏差在25 mm以内。而BCC-CSM1.1(m)模拟的降水量整体偏小,特别是大值降水量,当日降水量达到50 mm后,各台站降尺度前模拟降水量与实际的偏差普遍超过50 mm,而降尺度后整体的偏差不超过20 mm。所以SOM降尺度显著提高了模式对降水量PDF曲线尾部特征,即极端降水的模拟能力。
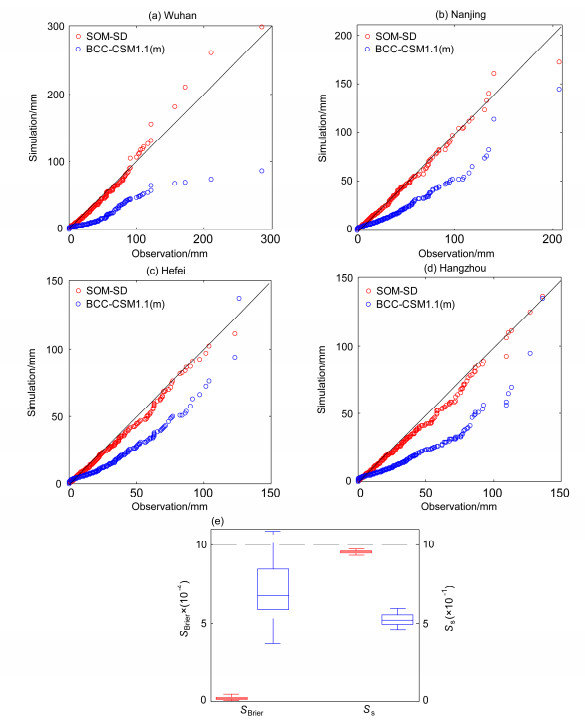
|
图 7 SOM降尺度(SOM-SD)和BCC-CSM1.1(m)模拟的(a)武汉、(b)南京、(c)合肥和(d)杭州站1986~2005年夏季逐日降水量和观测降水量Q-Q图及(e)所有台站日降水量概率分布曲线的SBrier和Ss盒须图 Fig. 7 Quantile-Quantile (Q-Q) plots between observed and simulated summer daily precipitation during 1986–2005 [both SOM downscaled (SOM-SD) and raw BCC-CSM1.1(m) outputs] at stations (a) Wuhan, (b) Nanjing, (c) Hefei, (d) Hangzhou, and (e) box plot of SBrier and Ss |
进一步考察降尺度对所有台站日降水量概率分布的模拟,计算各台站降尺度前后日降水量概率分布曲线与实际观测的SBrier和Ss指标。图 7e为SOM降尺度前后所有台站SBrier和Ss指标的盒须图。由图可见,虽然降尺度前后所有台站的SBrier数值都近似为0,但降尺度后的SBrier数值基本比降尺度前减少一个量级。降尺度后Ss全部在0.9以上,并且不同台站的SBrier和Ss指标离散程度小。而BCC-CSM1.1(m)模拟的SBrier不同台站的差异较大,Ss全部低于0.6。所以与全球模式相比,SOM降尺度改善了模式对降水量模拟偏弱的缺陷,提高了模式对日降水量概率分布的模拟能力。
4.2 降水场空间分布的模拟评估为对比评估降尺度前后降水场的空间分布的模拟能力,同样计算上文6个降水指数模拟与观测的相对误差百分率。图 8为降尺度前后各指数相对误差百分率的盒须图。可以看到,降尺度后,所有台站6个降水指数的相对误差百分率均小于耦合模式,偏差基本在20%以内并且不同台站偏差离散程度减小,说明SOM降尺度对降水频率和降水强度以及极端降水的模拟均优于BCC-CSM1.1(m)。降尺度后R1mm和R10mm为全局正偏差,偏差中位数在10%左右,而降尺度前模式对多数台站R1mm模拟的偏差超过40%,R10mm则为很大的负偏差,多数台站超过45%,降尺度后偏差减小了40%~50%,提高了模式对干湿日频率的模拟。降尺度对总降水量和平均日降水强度的模拟改善尤为明显,图 9给出降尺度前后总降水量和日降水强度的相对误差分布图。由图可见,除东部个别台站外,SOM降尺度模拟的夏季总降水量比观测偏多,多数台站偏差在15%以内。对于日降水强度,除西南部的少数台站为正偏差,其他台站为负偏差,数值多在5%以内。BCC-CSM1.1(m)模拟的总降水量和日降水强度均为全局很大的负偏差。GCMs普遍存在降水过于频繁,导致模拟的降水强度偏低(Sun et al., 2006),而SOM降尺度改善了模式对降水量模拟偏少和降水频率偏大的缺陷,提高了模拟的准确性。对于极端降水的模拟,降尺度后多数台站的日极端降水阈值比实际偏低,偏差在10%以内,正偏差出现在西部的个别台站(图略),而模式模拟的极端降水阈值为很大的负偏差。
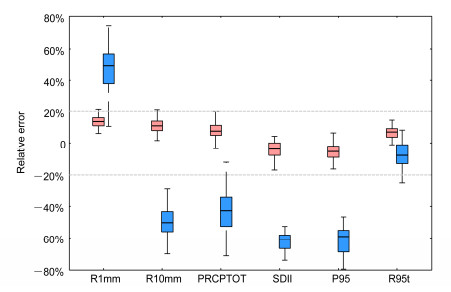
|
图 8 SOM降尺度和BCC-CSM1.1(m)模式模拟的台站夏季多年(1986~2005年)平均R1mm、R10mm、PRCPTOT、SDII、P95和R95t的相对误差百分率的盒须图。红色:SOM降尺度;蓝色:BCC-CSM1.1(m) Fig. 8 Box plot of relative errors' percentages of the simulated (both SOM downscaled and raw BCC-CSM1.1(m) outputs) mean R1mm, R10mm, PRCPTOT, SDII, P95, and R95t compared to observations during summer for the period 1986–2005. Red: SOM downscaled; blue: BCC-CSM1.1(m) |
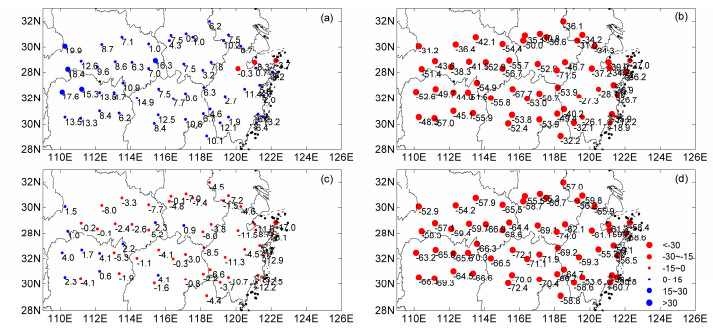
|
图 9 (a、c)SOM降尺度和(b、d)BCC-CSM1.1(m)模式模拟的夏季多年(1986~2005年)平均的(a、b)PRCPTOT和(c、d)SDII相对误差百分率(单位:%)空间分布 Fig. 9 Distributions of relative errors' percentages (units: %) of mean (a, b) PRCPTOT and (c, d) SDII for the (a, c) SOM downscaled simulated and (b, d) raw BCC-CSM1.1(m) outputs compared to observations during summer for the period 1986–2005 |
值得注意的是,虽然BCC-CSM1.1(m)对极端降水贡献率的模拟偏差小于其他5个指数,但由于BCC-CSM1.1(m)模拟的极端降水阈值偏小,总降水量也偏小,故由此计算得到的极端降水贡献率偏差不高,并无实际意义,即不能说明其对极端降水贡献率的模拟较好。降尺度后,极端降水阈值和总降水量均接近观测值,所以得到的极端降水贡献率偏差较小,多数台站在10%以内。
进一步利用泰勒图分析方法,考察降尺度前后降水指数空间分布的模拟效果。图 10为降尺度前后模拟与观测的6个降水指数的泰勒图。图中采用的数据是SOM降尺度模拟BCC-CSM1.1(m)模拟的多个降水指数与观测降水指数的相关系数、相对标准差以及均方根误差,SOM降尺度模拟的结果以红色表示,BCC-CSM1.1(m)以蓝色表示。可以看出,降尺度前所有指数与观测的相关系数均低于0.5,其中总降水量,日降水强度和极端降水阈值还出现负相关,而降尺度后6个指数与观测场的空间相关系数均在0.9以上。降尺度后6个指数的相对标准差均在1.0~1.5之间,说明降尺度后模拟场与观测场的空间变率相似,而降尺度前除极端降水贡献率外,其余的5个指数的相对标准差与参考点偏离较大。对于均方根误差,6个指数对应的数值均在0.5以下,其中R1mm、R10mm和总降水量的均方根误差在0.25以下,都比降尺度前有很大提高,说明SOM降尺度对6个降水指数的空间分布有较强的模拟效果,与BCC-CSM1.1(m)模式相比有很大的提高。
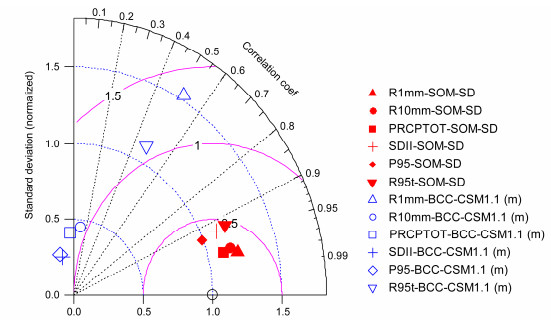
|
图 10 SOM降尺度和BCC-CSM1.1(m)模式模拟与观测的多年(1986~2005年)平均6个降水指数的泰勒图 Fig. 10 Taylor diagram of six mean summer precipitation-related indices between the observed and simulated (both SOM downscaled and raw BCC-CSM1.1 (m) outputs) values during 1986–2005 |
综上,SOM降尺度方法对降水场的空间分布具有较好的模拟效果。降尺度后所有台站各降水指数的相对误差百分率在20%以内,多数台站R10mm、总降水量和日降水强度的偏差在10%以内,与BCC-CSM1.1(m)模拟相比,偏差减小了40%~60%。降尺度后各降水指数气候场的空间相关系数均达到0.9,相对标准差接近1.0并且均方根误差在0.5以下。表明降尺度改善了模式对极端降水模拟偏弱的缺陷,提高了模拟的准确性。
5 结论和讨论本文引入一种基于SOM的统计降尺度方法,利用1961~1990年ERA-40数据和台站观测降水建立降尺度模型,通过独立样本检验该模型在江淮流域的模拟性能;进一步将SOM应用于BCC-CSM1.1 (m)模式,评估SOM降尺度方法是否具有“附加值”,具体结论如下:
(1) 通过降尺度目标台站所在区域的7个气象变量组成的逐日天气模态的SOM训练,可以得到20种频率分布较均匀,并且量化误差都低于10的主要天气模态,在此基础上,建立主要天气模态与各台站降水条件概率分布的关系,可以实现SOM降尺度建模。
(2) 独立样本检验表明SOM降尺度模拟的降水量与观测降水量具有较一致的日降水概率分布,所有降水指数区域平均的偏差不超过11%,空间相关在0.7以上,均方根误差较小,降尺度对极端降水也具有一定的模拟能力,并且能够在一定程度上模拟出江淮流域夏季降水的时间变率,多数台站的中雨日数和极端降水贡献率的IMV指数在0.5以内。
(3) 将SOM降尺度模型运用到BCC-CSM1.1(m)模式中,降尺度后的日降水概率分布与观测基本一致,显著改善了模式对极端降水模拟偏弱的缺陷,对不同降水指数的模拟较BCC-CSM1.1(m)模式显著提高,降尺度后所有台站各降水指数的相对误差百分率与模式相比减小了40%~60%,空间相关系数均提高到0.9,相对标准差接近1.0,并且均方根误差在0.5以下,提高了模式对降水的模拟能力。
SOM统计降尺度方法利用SOM在识别大气真实天气模态及其演变过程中的优势,建立主要天气模态与局地降水条件分布函数的非线性、多模态的关系,相比其他统计降尺度方法建立的单一关系更为稳定,并且认为将该方法应用于未来降水预估时,天气型及其与局地降水的关系不会变化,但每种天气型在未来的发生频率变化,进而使降水发生变化。Ning et al.(2012b)在研究中指出,利用该方法建立的降尺度模型具有一定的平稳性。未来利用该方法进行江淮流域降水预估时,还需进一步研究。综上,将SOM降尺度方法引入到江淮流域的降水研究中,实现了逐日降水的降尺度,对BCC-CSM1.1(m)模拟结果的降尺度应用表明,该方法显著提高模式对日降水概率分布、特别是降水PDF曲线尾部特征的模拟能力,改善了极端降水场的模拟能力,为提高未来预估能力提供了基础。
| [] | Chen W L, Jiang Z H, Li L. 2011. Probabilistic projections of climate change over China under the SRES A1B scenario using 28 AOGCMs[J]. J. Climate , 24 (17) : 4741–4756. DOI:10.1175/2011JCLI4102.1 |
| [] | 陈晓晨, 徐影, 许崇海, 等. 2014. CMIP5全球气候模式对中国地区降水模拟能力的评估[J]. 气候变化研究进展 , 10 (3) : 217–225. Chen Xiaochen, Xu Ying, Xu Chonghai, et al. 2014. Assessment of precipitation simulations in China by CMIP5 multi-models[J]. Advances in Climate Change Research (in Chinese) , 10 (3) : 217–225. DOI:10.3969/j.issn.1673-1719.2014.03.011 |
| [] | 陈晓晨, 徐影, 姚遥. 2015. 不同升温阈值下中国地区极端气候事件变化预估[J]. 大气科学 , 39 (6) : 1123–1135. Chen Xiaochen, Xu Ying, Yao Yao. 2015. Changes in climate extremes over China in a 2℃, 3℃, and 4℃ warmer world[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 39 (6) : 1123–1135. DOI:10.3878/j.issn.1006-9895.1502.14224 |
| [] | Chu J E, Hameed S N, Ha K J. 2012. Nonlinear, intraseasonal phases of the East Asian summer monsoon:Extraction and analysis using Self-Organizing Maps[J]. J. Climate , 25 (20) : 6975–6988. DOI:10.1175/JCLI-D-11-00512.1 |
| [] | 崔妍, 江志红, 陈威霖. 2010. 典型相关分析方法对21世纪江淮流域极端降水的预估试验[J]. 气候变化研究进展 , 6 (6) : 405–410. Cui Yan, Jiang Zhihong, Chen Weilin. 2010. Projection of extreme precipitation events in the 21st century in the Changjiang-Huaihe River valley based on canonical correlation analysis[J]. Advances in Climate Change Research (in Chinese) , 6 (6) : 405–410. |
| [] | Ding Y H. 1994. Monsoons over China[J]. Advances in Atmospheric Sciences , 11 (2) : 252–252. DOI:10.1007/BF02666553 |
| [] | 范丽军, 符淙斌, 陈德亮. 2005. 统计降尺度法对未来区域气候变化情景预估的研究进展[J]. 地球科学进展 , 20 (3) : 320–329. Fan Lijun, Fu Congbin, Chen Deliang. 2005. Review on creating future climate change scenarios by statistical downscaling techniques[J]. Advances in Earth Science (in Chinese) , 20 (3) : 320–329. DOI:10.11867/j.issn.1001-8166.2005.03.0320 |
| [] | 范丽军, 符淙斌, 陈德亮. 2007. 统计降尺度法对华北地区未来区域气温变化情景的预估[J]. 大气科学 , 31 (5) : 887–897. Fan Lijun, Fu Congbin, Chen Deliang. 2007. Estimation of local temperature change scenarios in North China using statistical downscaling method[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 31 (5) : 887–897. DOI:10.3878/j.issn.1006-9895.2007.05.12 |
| [] | Frich P, Alexander L V, Della-Marta P, et al. 2002. Observed coherent changes in climatic extremes during the second half of the twentieth century[J]. Climate Research , 19 : 193–212. DOI:10.3354/cr019193 |
| [] | Fu G B, Liu Z F, Charles S P, et al. 2013. A score-based method for assessing the performance of GCMs:A case study of southeastern Australia[J]. J. Geophys. Res. , 118 (10) : 4154–4167. DOI:10.1002/jgrd.50269 |
| [] | 高学杰, 徐影, 赵宗慈, 等. 2006. 数值模式不同分辨率和地形对东亚降水模拟影响的试验[J]. 大气科学 , 30 (2) : 185–192. Gao Xuejie, Xu Ying, Zhao Zongci, et al. 2006. Impacts of horizontal resolution and topography on the numerical simulation of East Asian precipitation[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 30 (2) : 185–192. DOI:10.3878/j.issn.1006-9895.2006.02.01 |
| [] | Gleckler P J, Taylor K E, Doutriaux C. 2008. Performance metrics for climate models[J]. J. Geophys. Res. , 113 (D6) : D06104. DOI:10.1029/2007JD008972 |
| [] | 郭彦, 李建平. 2012. 一种分离时间尺度的统计降尺度模型的建立和应用——以华北汛期降水为例[J]. 大气科学 , 36 (2) : 385–396. Guo Yan, Li Jianping. 2012. A time-scale decomposition statistical downscaling model:Case study of North China rainfall in rainy season[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 36 (2) : 385–396. DOI:10.3878/j.issn.1006-9895.2011.11045 |
| [] | Hewitson B C, Crane R G. 2002. Self-Organizing maps:Applications to synoptic climatology[J]. Climate Research , 22 (1) : 13–26. DOI:10.3354/cr022013 |
| [] | Hewitson B C, Crane R G. 2006. Consensus between GCM climate change projections with empirical downscaling:Precipitation downscaling over South Africa[J]. International Journal of Climatology , 26 (10) : 1315–1337. DOI:10.1002/joc.1314 |
| [] | 胡娅敏, 丁一汇. 2009. 2000年以来江淮梅雨带北移的可能成因分析[J]. 气象 , 35 (12) : 37–43. Hu Yamin, Ding Yihui. 2009. Possible reasons for northward shift of Meiyu belt in Yangtze-Huaihe River region during 2000-2005[J]. Meteorological Monthly (in Chinese) , 35 (12) : 37–43. DOI:10.7519/j.issn.1000-0526.2009.12.005 |
| [] | 黄海玲, 江志红, 王志福, 等. 2015. CMIP5模式对东亚500 hPa高度场主要模态时空结构模拟能力的评估[J]. 气象学报 , 73 (1) : 110–127. Huang Hailing, Jiang Zhihong, Wang Zhifu, et al. 2015. The evaluation of the 500 hPa geopotential height's main modes in East Asia as done by the CMIP5 models[J]. Acta Meteorologica Sinica (in Chinese) , 73 (1) : 110–127. |
| [] | 贾小龙, 陈丽娟, 李维京, 等. 2010. BP-CCA方法用于中国冬季温度和降水的可预报性研究和降尺度季节预测[J]. 气象学报 , 68 (3) : 398–410. Jia Xiaolong, Chen Lijuan, Li Weijing, et al. 2010. Statistical downscaling based on BP-CCA:Predictability and application to the winter temperature and precipitation in China[J]. Acta Meteorologica Sinica (in Chinese) , 68 (3) : 398–410. |
| [] | 江志红, 陈威霖, 宋洁, 等. 2009. 7个IPCC AR4模式对中国地区极端降水指数模拟能力的评估及其未来情景预估[J]. 大气科学 , 33 (1) : 109–120. Jiang Zhihong, Chen Weilin, Song Jie, et al. 2009. Projection and evaluation of the precipitation extremes indices over China based on seven IPCC AR4 coupled climate models[J]. Chinese Journal of Atmospheric Sciences (in Chinese) , 33 (1) : 109–120. DOI:10.3878/j.issn.1006-9895.2009.01.10 |
| [] | Kohonen T. 1982. Self-Organized formation of topologically correct feature maps[J]. Biological Cybernetics , 43 (1) : 59–69. DOI:10.1007/BF00337288 |
| [] | Kohonen T. 2000. Self-Organizing Maps[M]. 3rd ed: Berlin:Springer: 153 -160. |
| [] | Lall U, Sharma A. 1996. A nearest neighbor bootstrap for resampling hydrologic time series[J]. Water Resour. Res. , 32 (3) : 679–693. DOI:10.1029/95WR02966 |
| [] | 梁萍, 丁一汇, 何金海. 2008. 长江下游夏季降水与东亚夏季风及春季太平洋海温的关系[J]. 高原气象 , 27 (4) : 772–777. Liang Ping, Ding Yihui, He Jinhai. 2008. Relations between summer rainfall over the lower reach of Yangtze River and East Asian summer monsoon as well as sea surface temperature over the Pacific in spring[J]. Plateau Meteorology (in Chinese) , 27 (4) : 772–777. |
| [] | Ning L, Mann M E, Crane R, et al. 2012a. Probabilistic projections of climate change for the mid-Atlantic region of the United States:Validation of precipitation downscaling during the historical Era[J]. J. Climate , 25 (2) : 509–526. DOI:10.1175/2011JCLI4091.1 |
| [] | Ning L, Mann M E, Crane R, et al. 2012b. Probabilistic projections of anthropogenic climate change impacts on precipitation for the mid-Atlantic region of the United States[J]. J. Climate , 25 (15) : 5273–5291. DOI:10.1175/JCLI-D-11-00565.1 |
| [] | Perkins S E, Pitman A J, Holbrook N J, et al. 2007. Evaluation of the AR4 climate models' simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions[J]. J. Climate , 20 (17) : 4356–4376. DOI:10.1175/JCLI4253.1 |
| [] | Radić V, Clarke G K C. 2011. Evaluation of IPCC models' performance in simulating late-twentieth-century climatologies and weather patterns over North America[J]. J. Climate , 24 (20) : 5257–5274. DOI:10.1175/JCLI-D-11-00011.1 |
| [] | Santer B D, Taylor K E, Gleckler P J, et al. 2009. Incorporating model quality information in climate change detection and attribution studies[J]. Proceedings of the National Academy of Sciences of the United States of America , 106 (35) : 14778–14783. DOI:10.1073/pnas.0901736106 |
| [] | Sun Y, Solomon S, Dai A G, et al. 2006. How often does it rain?[J]. Climate , 19 (6) : 916–934. DOI:10.1175/JCLI3672.1 |
| [] | Taylor K E. 2001. Summarizing multiple aspects of model performance in a single diagram[J]. J. Geophys. Res. , 106 (D7) : 7183–7192. DOI:10.1029/2000JD900719 |
| [] | Trenberth K E. 1998. Atmospheric moisture residence times and cycling:Implications for rainfall rates and climate change[J]. Climatic Change , 39 (4) : 667–694. DOI:10.1023/A:1005319109110 |
| [] | Trenberth K E, Dai A G, Rasmussen R M, et al. 2003. The changing character of precipitation[J]. Bull. Amer. Meteor. Soc. , 84 (9) : 1205–1217. DOI:10.1175/BAMS-84-9-1205 |
| [] | Uppala S M, Kållberg P W, Simmons A J, et al. 2005. The ERA-40 re-analysis[J]. Quart. J. Roy. Meteor. Soc. , 131 (612) : 2961–3012. DOI:10.1256/qj.04.176 |
| [] | 王冀, 江志红, 宋洁, 等. 2008. 基于全球模式对中国极端气温指数模拟的评估[J]. 地理学报 , 63 (3) : 227–236. Wang Ji, Jiang Zhihong, Song Jie, et al. 2008. Evaluating the simulation of the GCMs on the extreme temperature indices in China[J]. Acta Geographica Sinica (in Chinese) , 63 (3) : 227–236. |
| [] | Wang Y D, Jiang Z H, Chen W L. 2015. Performance of CMIP5 models in the simulation of climate characteristics of synoptic patterns over East Asia[J]. J. Meteor. Res. , 29 (4) : 594–607. DOI:10.1007/s13351-015-4129-4 |
| [] | 许崇海, 罗勇, 徐影. 2010. 全球气候模式对中国降水分布时空特征的评估和预估[J]. 气候变化研究进展 , 6 (6) : 398–404. Xu Chonghai, Luo Yong, Xu Ying. 2010. Assessment and projection for spatial-temporal distribution of precipitation in China based on Global Climate Models[J]. Advances in Climate Change Research (in Chinese) , 6 (6) : 398–404. |
| [] | Yin C H, Li Y P, Ye W, et al. 2011. Statistical downscaling of regional daily precipitation over Southeast Australia based on self-organizing maps[J]. Theor. Appl. Climatol. , 105 (1-2) : 11–26. DOI:10.1007/s00704-010-0371-y |
| [] | Zhang X B, Alexander L, Hegerl G C, et al. 2011. Indices for monitoring changes in extremes based on daily temperature and precipitation data[J]. Wiley Interdisciplinary Reviews:Climate Change , 2 (6) : 851–870. DOI:10.1002/wcc.147 |
| [] | Zhu C W, Park C K, Lee W S, et al. 2008. Statistical downscaling for multi-model ensemble prediction of summer monsoon rainfall in the Asia-Pacific region using geopotential height field[J]. Advances in Atmospheric Sciences , 25 (5) : 867–884. DOI:10.1007/s00376-008-0867-x |
 2016, Vol. 21
2016, Vol. 21


