2 中国科学院大气物理研究所国际气候与环境科学中心, 北京 100029;
3 中国气象局国家气象信息中心, 北京 100081
2 International Center for Climate and Environment Sciences(ICCES), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3 National Meteorological Information Center, China Meteorological Administration, Beijing 100081
提高大气温度数据的精确度,合理准确地估计温度变化趋势,对于基础天气预报及气候、农业与环境研究均有重要意义。地面观测站数据具有较高的可信度,但就中国区域而言,观测站点在空间分布上存在明显的不连续,呈现东密西疏状态,对基于地面观测的格点数据质量有较大影响(Chen et al., 2010;熊秋芬等,2011)。对数据的融合处理近年来得到广泛发展,所谓数据融合技术,是指将多平台、多传感器的采集信息加以综合,进而获得关于目标区规范化网格的标准化定量信息(苗春生等,2015)。数据融合技术的发展主线,一直以来主要是降水资料和海温资料。研究表明适当的融合方法能有效发挥观测数据的优势,同时使得融合产品接近观测值,以更合理的方式分布于格点中(苗春生等,2015;宇婧婧等,2015)。
气象观测站点数据作为一种空间数据,具有复杂的非线性动力学机制,在时空分布上纷杂多变,因此实际使用中通常需要将这种离散的、不规则的观测资料转换成规则的、可以用于数值模拟的初始场或者诊断分析所用的规则网格点资料。通常采用的方法即为“空间内插”,常用的方法有:样条函数法、克里金(Kriging)插值法、距离平方反比法和Cressman插值法(Cressman, 1959)等。克里金法计算量大、过程复杂,变异函数需要人为选定,而样条函数插值难以对误差进行估计,采样点稀少时效果不好(冯锦明等,2004)。距离平方反比则是计算比较便捷的插值方法,相比较于逐步订正的Cressman插值,Cressman客观分析具有更小的相对误差(冯锦明等,2004),在气象数据融合领域应用广泛。
美国NOAA(National Oceanic and Atmospheric Administration)下属的地球系统研究实验室(Earth System Research Laboratory,简称ESRL)开发的解决资料融合问题的局地分析预报系统(Local Analysis and Prediction System,简称LAPS)包括两种资料融合方法,一种是基于修正Barnes插值方法,另一种是基于连续变分的方法,即STMAS方法(Space–Time Multiscale Analysis System)。STMAS方法是由Xie et al.(2005, 2011)发展起来的新的资料融合方法,结合了统计分析(如3DVar或EnKF)和传统客观的分析(如Barnes分析)的优势,通过采用多重网格策略依次对不同尺度的观测信息进行分析,消除长波信息与短波信息之间的干扰。多重网格策略主要是对观测数据的处理上采用稀疏化。稀疏化是指由于观测资料分布不均匀,对于每个网格内的观测数据,观测点个数不同,尤其是粗网格,这时可以先将一个网格内的观测数据插值到该网格中心点,做成一个数据观测点。STMAS方法对于背景误差协方差和观测误差协方差的考虑较为简化,认为二者比值为常数,融合产品的精度也有待检验。
无论是融合方案还是空间插值,都是对观测数据或者各种平台数据的进一步优化处理。数据融合方面的研究,对气温数据的融合研究甚少,因此本文通过将基于多重网格策略的NLS-3DVar(Non-linear least squares-based 3D variational data assimilation system)方法(Tian and Feng, 2015)融合气温数据,并与Cressman插值的结果进行对比分析,进一步验证NLS-3DVar方法的合理性和优越性。第二节介绍了本文研究所用到的数据资料,多重网格策略下的三维变分同化方法,包括NLS-3DVar算法和STMAS算法的理论依据,以及气象行业广泛应用的Cressman插值算法,同时给出了试验设计和检验方法。第三节比较了单重网格下NLS-3DVar和Cressman插值的融合产品。第四节对比单、双重网格下NLS-3DVar产品的差异,并与STMAS算法进行比较。第五节总结了本研究得到的结论。
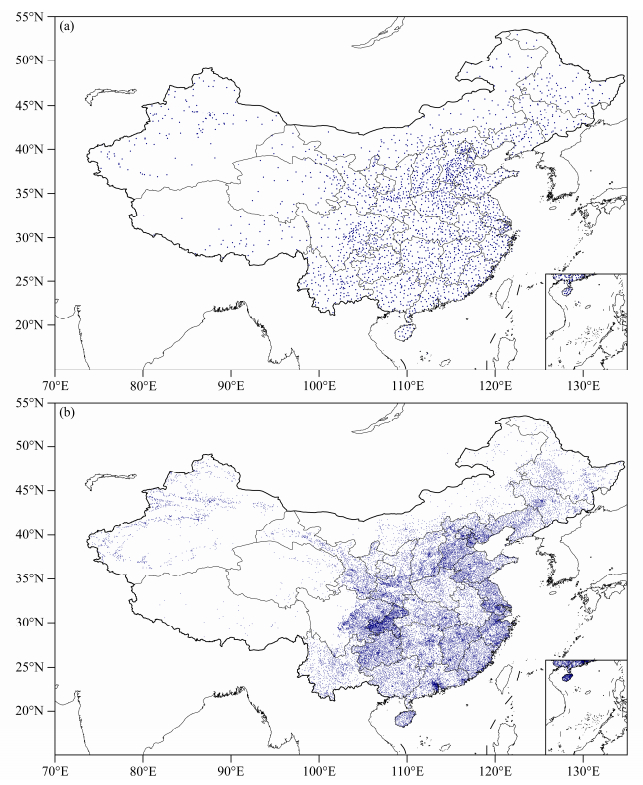
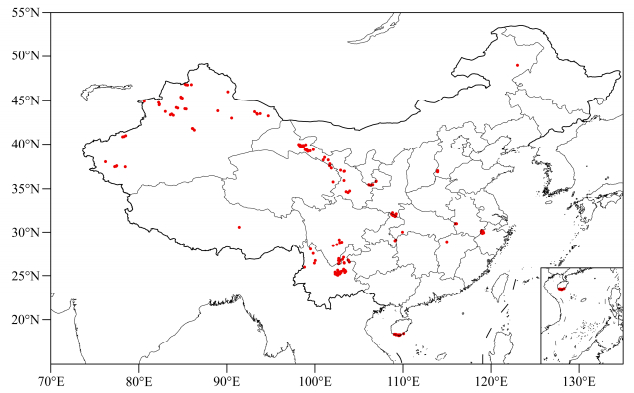
2 资料与方法 2.1 大气温度数据融合的温度数据源包括地面观测和NCEP(National Centers for Environmental Prediction)再分析数据(Final Global Tropospheric Analyses)。其中,地面观测温度数据为中国2400多个国家级地面气象观测站(图 1a)的逐小时观测值(00时至次日00时,协调世界时,下同),经过严格的质量控制(任芝花等,2015)。NCEP再分析数据覆盖全球范围,本文中选取中国区域(16°N~55°N,70°E~135°E),数据空间分辨率1°×1°,时间分辨率为6小时,本文以此数据为背景场资料,进行下述研究。所用数据时间序列为2014年1月1日至2014年12月31日。本文将该时空,该区域的NCEP再分析数据作为背景场资料,将中国2400多个国家级地面气象观测站的气温资料与之融合。用于独立样本检验的数据是全国30000多个全国自动气象站(图 1b)逐时气温数据,由于自动站数据在2014年4月、5月存在大量缺测,因此在独立检验时去除4月和5月。由于2400多个国家级地面观测站数据在准确度和站点分布上较区域自动站更精准更合理,故用于融合,区域自动站数据用于独立检验,具体的检验方法详见2.5。
|
图 1 (a)中国2400多个国家级气象站分布,(b)中国3万余个自动观测站(包括国家站和区域站)分布 Fig. 1 Distributions of (a) more than 2400 national automatic weather stations (AWS) and (b) more than 30, 000 national and regional AWS over China |
多重网格的三维变分同化方法可以依次从大尺度和小尺度上采用连续的三维变分更准确地使误差最小化。多重网格三维变分较传统三维变分的优势在于依次从观测提取长波和短波信息组成一个从粗网格到细网格的连续的多尺度三维变分方案。其代价函数形式为
| $ \begin{array}{c} {J^{(k)}}({{\boldsymbol{x'}}^{(k)}}) = \frac{1}{2}{({{\boldsymbol{x'}}^{(k)}})^{\rm{T}}}{\left( {{\boldsymbol{B}^{(k)}}} \right)^{ - 1}}({{\boldsymbol{x'}}^{(k)}}) + \\ \frac{1}{2}{\left[ {{\boldsymbol{H}^{(k)}}(\boldsymbol{x}_{\rm{b}}^{(k)} + {{\boldsymbol{x'}}^{(k)}}) - \boldsymbol{y}_{{\rm{obs}}}^{(k)}} \right]^T}{\boldsymbol{R}^{(k) - 1}} \times \\ \left[ {{\boldsymbol{H}^{(k)}}(\boldsymbol{x}_{\rm{b}}^{(k)} + {{\boldsymbol{x'}}^{(k)}}) - \boldsymbol{y}_{{\rm{obs}}}^{(k)}} \right],{\rm{ }}(k = 1,{\rm{ }}2,\;...,\;S), \end{array} $ | (1) |
其中,
本文所使用的数据融合方法——基于多重网格的NLS-3DVar(即非线性最小二乘法三维变分同化方法)方法是对Tian and Feng(2015)所提出的NLS-4DVar的三维版本,通过将多重网格策略引入,并利用NCEP再分析数据构造集合样本近似背景误差协方差矩阵B,采用扩展局地化策略(Liu et al., 2008; Tian et al., 2016),形成一种计算更高效更准确的多重网格的三维变分同化方法。
基于多重网格的连续变分同化方法STMAS方法是一种简化的多重网格三维变分方案,其简化主要体现在对背景误差协方差和观测误差协方差的常数比处理上。下面进一步分别介绍这两种方法。
2.2.1 基于多重网格策略的NLS-3DVar方法NLS-3DVar方法的主要思想是利用集合策略求解以下代价函数的最小值:
| $ \begin{array}{c} J(\boldsymbol{x'}) = \frac{1}{2}{(\boldsymbol{x'})^T}{\boldsymbol{B}^{ - 1}}(\boldsymbol{x'}) + \frac{1}{2}{\left[ {\boldsymbol{H}({\boldsymbol{x}_{\rm{b}}} + \boldsymbol{x'}) - {\boldsymbol{y}_{{\rm{obs}}}}} \right]^T} \times \\ {\boldsymbol{R}^{ - 1}}\left[ {\boldsymbol{H}({\boldsymbol{x}_{\rm{b}}} + \boldsymbol{x'}) - {\boldsymbol{y}_{{\rm{obs}}}}} \right], \end{array} $ | (2) |
其中,
| $ {{\boldsymbol{y'}}_{{\rm{obs}}}} = {\boldsymbol{y}_{{\rm{obs}}}} - \boldsymbol{H}({\boldsymbol{x}_{\rm{b}}}) $ | (3) |
| $ {{\boldsymbol{x'}}_{\rm{a}}} = {\boldsymbol{P}_x}\boldsymbol{\beta }, $ | (4) |
这里
将(4)式带入(2)式,代价函数形式改写为
| $ \begin{array}{c} J(\boldsymbol{\beta }) = \frac{1}{2}{\boldsymbol{\beta }^{\rm{T}}}{({\boldsymbol{P}_x})^{\rm{T}}}{\boldsymbol{B}^{ - 1}}({\boldsymbol{P}_x})\boldsymbol{\beta } + \frac{1}{2}{\left[ {\boldsymbol{H}({\boldsymbol{x}_{\rm{b}}} + {\boldsymbol{P}_x}\boldsymbol{\beta }) - {\boldsymbol{y}_{{\rm{obs}}}}} \right]^T} \times \\ {\boldsymbol{R}^{ - 1}}\left[ {\boldsymbol{H}({\boldsymbol{x}_{\rm{b}}} + {\boldsymbol{P}_x}\boldsymbol{\beta }) - {\boldsymbol{y}_{{\rm{obs}}}}} \right]. \end{array} $ | (5) |
根据Evensen(2004)和Tian et al.(2011),背景误差协方差
| $ J(\boldsymbol{\beta }) = \frac{1}{2}Q{(\boldsymbol{\beta })^{\rm{T}}}Q(\boldsymbol{\beta }), $ | (6) |
其中,
| $ Q(\boldsymbol{\beta }){\rm{ = }}\left( \begin{array}{l} \mathrm{R}_{\text{+}}^{-{}^{1}\!\!\diagup\!\!{}_{2}\;}\left[ {L'\left( {{\boldsymbol{P}_x}\boldsymbol{\beta }} \right) - {{\boldsymbol{y'}}_{{\rm{obs}}}}} \right]\\ \sqrt {N - 1} \boldsymbol{\beta } \end{array} \right). $ | (7) |
由此可用以下的高斯—牛顿迭代法(Dennis and Schnabel, 1996)进行迭代求解:
| $ \begin{array}{c} {\boldsymbol{\beta }^{i + 1}} = {\boldsymbol{\beta }^i} - {\left[ {{{({\boldsymbol{P}_y})}^{\rm{T}}}{\boldsymbol{R}^{ - 1}}({\boldsymbol{P}_y}) + (N - 1)\boldsymbol{I}} \right]^{ - 1}} \cdot \\ \left[ {{{({\boldsymbol{P}_y})}^{\rm{T}}}{\boldsymbol{R}^{ - 1}}(L'(\boldsymbol{x'}_{\rm{a}}^{,i}) - {{\boldsymbol{y'}}_{{\rm{obs}}}}) + (N - 1){\boldsymbol{\beta }^i}} \right], \end{array} $ | (8) |
其中,
对于集合估计的背景误差协方差矩阵有
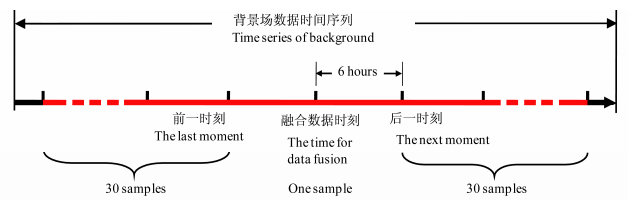
|
图 2 历史采样法示意图 Fig. 2 Sketch map of historical sampling |
完成采样之后,计算
对局地化相关矩阵C做类似的分解(Liu et al., 2009; Tian et al., 2016):
| $ {\boldsymbol{P}_{x{\rm{,}}\rho }} = {\boldsymbol{P}_x} < e > \boldsymbol{C'} = (\boldsymbol{C'} \circ \boldsymbol{P}_{x,1}^*,\boldsymbol{C'} \circ \boldsymbol{P}_{x,2}^*, \cdots ,\boldsymbol{C'} \circ \boldsymbol{P}_{x,N}^*), $ | (9) |
式中,“
| $ {\boldsymbol{P}_{y{\rm{,}}\rho }} = {\boldsymbol{P}_y} < e > \boldsymbol{C'} = (\boldsymbol{C'} \circ \boldsymbol{P}_{y,1}^*,\boldsymbol{C'} \circ \boldsymbol{P}_{y,2}^*, \cdots ,\boldsymbol{C'} \circ \boldsymbol{P}_{y,N}^*), $ | (10) |
其中,
| $ \begin{array}{c} {\boldsymbol{\beta }^{i + 1}} = {\boldsymbol{\beta }^i} - {\left[ {{{({\boldsymbol{P}_{y,\rho }})}^{\rm{T}}}{\boldsymbol{R}^{ - 1}}({\boldsymbol{P}_{y,\rho }}) + (N - 1)\boldsymbol{I}} \right]^{ - 1}} \times \\ \left[ {{{({\boldsymbol{P}_{y,\rho }})}^{\rm{T}}}{\boldsymbol{R}^{ - 1}}(L'(\boldsymbol{x'}_{\rm{a}}^{,i}) - {{\boldsymbol{y'}}_{{\rm{obs}}}}) + (N - 1){\boldsymbol{\beta }^i}} \right]. \end{array} $ | (11) |
最后采用共轭梯度法迭代求得
按照多重网格策略,一方面要对每一重网格下用于融合的观测数据做稀疏化处理,即将一个网格内的观测数据插值到该网格中心点,做成一个数据观测点,本研究中采用的是距离反比插值;另一方面,从粗网格转换到细网格时,其观测误差协方差R也应当做相应的调整:
| $ \boldsymbol{R}_k^2 = \sum\limits_{i = 1}^{{n_k}} {a_i^2\boldsymbol{R}_0^2} {\rm{, }}k{\rm{ = 1, 2, }}...{\rm{, }}S{\rm{,}} $ | (12) |
其中,R0为初始的观测误差,本研究取0.5℃,Rk是第k重网格下的观测误差协方差,S是网格总层数,a是对某一个网格内观测数据做稀疏化处理时,各个观测点插值到网格中心时的插值系数,nk是第k重网格下每个网格内观测站点的数目;而Bk在每层网格下的构造,则取决于不同分辨率网格下选取的样本。
粗网格向细网格转换的桥梁是粗网格下生成的分析场结果,通过将其插值到细网格的分辨率下,作为细网格的背景场,继续进行该分辨率下的数据融合。
2.2.2 STMAS算法按照基于多重网格的连续变分同化方法STMAS方法对于B和R的简化思路,(1)式的代价函数简写为(Li et al., 2013)
| $ \begin{array}{c} {J^{(k)}}\left( {{\boldsymbol{X}^{(k)}}} \right) = \frac{1}{2}{\boldsymbol{X}^{(k)T}}{\boldsymbol{X}^{(k)}} + \frac{1}{2}{\left[ {{\boldsymbol{H}^{(k)}}{\boldsymbol{X}^{(k)}} - {\boldsymbol{Y}^{(k)}}} \right]^{\rm{T}}} \times \\ {\boldsymbol{O}^{(k) - 1}}\left[ {{\boldsymbol{H}^{(k)}}{\boldsymbol{X}^{(k)}} - {{\bf{Y}}^{(k)}}} \right]{\rm{, }}k = 1,{\rm{ }}2,{\rm{ }}...,{\rm{ }}S, \end{array} $ | (13) |
其中,
| $ {\boldsymbol{Y}^{(k)}} = {\boldsymbol{Y}^{(k - 1)}} - {\boldsymbol{H}^{(k - 1)}}{\boldsymbol{X}^{(k - 1)}}{\rm{, }}k = 1,{\rm{ }}2,{\rm{ }}...,{\rm{ }}S, $ | (14) |
| $ {\boldsymbol{X}_{\rm{a}}} = {\boldsymbol{X}_{\rm{b}}} + \sum\limits_{k = 1}^S {{\boldsymbol{X}^{(k)}}} . $ | (15) |
本研究中取网格层数
一般的数据融合方法,都是在单重网格下进行,直接将观测数据融合生成最细分辨率的产品。已被广泛应用于各种气候诊断分析和数值模拟研究中的Cressman插值具有相对于其他插值方案更小的相对误差。本研究中,在最细分辨率1°×1°的单重网格下,对比NLS-3DVar方法和Cressman插值的融合产品。下面介绍Cressman插值方法。
首先给定第一猜测场,一般网格的第一猜测场由背景场给出:
| $ T_i^{n + 1} = T_i^n + \frac{{\sum\limits_{k = 1}^{{K_i}} {{W^n}({r_{ik}})(T_k^{{\rm{obs}}} - T_i^n)} }}{{{\varepsilon ^2} + \sum\limits_{k = 1}^{{K_i}} {W({r_{ik}})} }}, $ | (16) |
式中,
| $ W({r_{ik}}) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{r_{ik}}^2 - d_{ik}^2}}{{{r_{ik}}^2 + d_{ik}^2}}{\rm{,}}}&{{d_{ik}} < {r_{ik}},}\\ {0,}&{{d_{ik}} \ge {r_{ik}},} \end{array}} \right. $ | (17) |
其中,dik是第k个站点到待插值格点i的距离。影响半径r的选取原则是由近及远进行扫描。
本文中采用该插值方法,将2400多个国家级地面气象观测站点数据插值至分辨率为1°×1°的网格中,影响半径取0.5°至4°(55 km~220 km)。
2.4 试验设计本文设置了三组对比试验来检验基于多重网格策略的NLS-3DVar融合产品的质量。表 1给出了三组试验设计方案。通过试验一在单重网格下的对比,验证采用NLS-3DVar方法得到的气温融合产品在精度上的优势。试验二对同一方案NLS-3DVar的不同网格数目的产品的对比,直观展示多重网格策略引入后产品精度和计算效率的变化。试验三有两个目的,一是检验STMAS算法中对误差矩阵的简化处理是否合适,二是对比这两种方案在同时采用双重网格策略的情况下,产品精度和计算效率的差异。通过三组试验,充分证明基于多重网格策略的NLS-3DVar资料融合方法所生成的融合产品在精度和计算效率上的优越性。
|
|
表 1 三组试验设计 Table 1 Design of three groups of experiments |
为了更好的评估NLS-3DVar方法、Cressman插值以及STMAS算法的分析精度,需要进行独立样本检验,即选取完全独立于融合产品的气温资料作为参考。本研究所用经过严格质量控制(任芝花等,2015)的30000多个全国自动气象观测站(图 1b)逐时气温资料,剔除用于数据融合所用到的2400多个国家级地面气象站(图 1a)数据。为进一步保证数据质量,剔除了四个研究时次(00时、06时、12时、18时)均为缺测的区域站点,将剩余的区域自动气象站气温资料作为独立检验数据。为了进一步保证检验数据的有效与合理性,筛选了国家站所在网格内(1°×1°的网格)的自动台站资料作为独立样本,称其为“有效独立样本”(18000多个)。鉴于背景场NCEP数据时间分辨率为6小时(00时、06时、12时、18时),所以融合逐小时观测数据后的融合产品亦只有4个时次,分辨率同样为1°×1°。独立样本检验时间序列为2014年1~12月(4月、5月由于独立检验样本缺测,亦去除)。为了与融合产品比较,检验时,通过距离反比插值将融合产品插值至有效独立样本所在站点,计算统计误差。定量误差估计的统计指标主要有均方根误差(RRMSE),规范化的标准差(SSDV)和相关系数(CCov)。SDV表示融合产品结果与观测的相近程度,越接近1,效果越好。定义公式如下:
| $ {C_{{\rm{cov}}}} = \frac{{\sum\limits_{i = 1}^M {({x_{i,{\rm{obs}}}} - \overline {{x_{{\rm{obs}}}}} )({y_{i,{\rm{model}}}} - \overline {{y_{{\rm{model}}}}} )} }}{{\sqrt {\sum\limits_{i = 1}^M {{{({x_{i,{\rm{obs}}}} - \overline {{x_{{\rm{obs}}}}} )}^2}} } \sqrt {\sum\limits_{i = 1}^M {{{({y_{i,{\rm{model}}}} - \overline {{y_{{\rm{model}}}}} )}^2}} } }}, $ | (18) |
| $ {S_{{\rm{SDV}}}} = \frac{{\sqrt {\sum\limits_{i = 1}^M {{{({y_{i,{\rm{model}}}} - \overline {{y_{{\rm{model}}}}} )}^2}} /M} }}{{\sqrt {\sum\limits_{i = 1}^M {{{({x_{i,{\rm{obs}}}} - \overline {{x_{{\rm{obs}}}}} )}^2}/M} } }}, $ | (19) |
| $ {R_{{\rm{RMSE}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^M {{{{\rm{(}}{x_{i,{\rm{obs}}}} - {y_{i,{\rm{model}}}}{\rm{)}}}^2}} }}{M}} , $ | (20) |
其中,M为样本总数,根据计算变量的不同,M分为时间序列样本总数和站点序列样本总数两种,
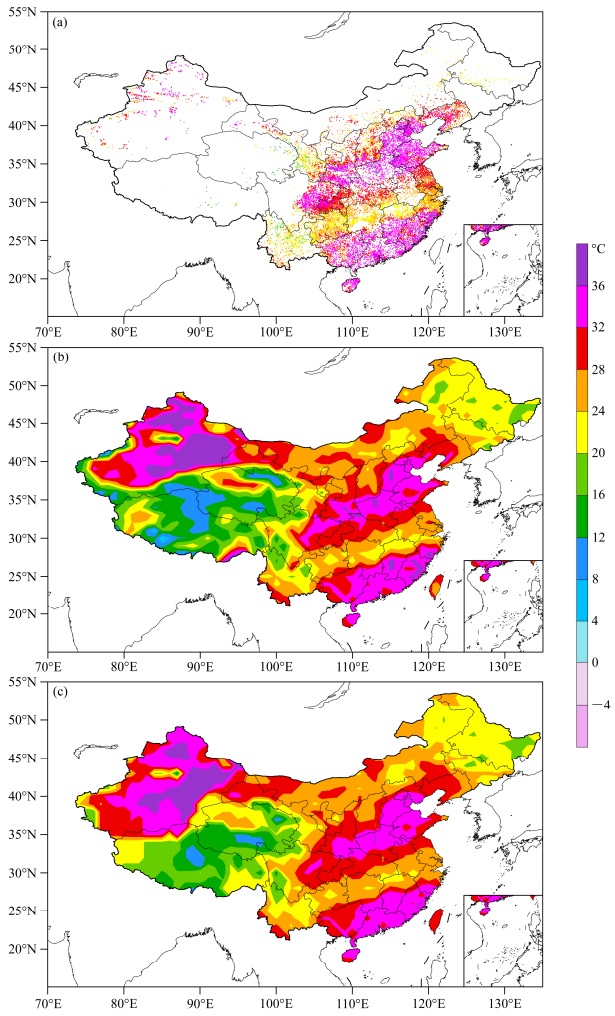
图 3展示了2014年7月13日06时的气温场结果。直观来看,两种产品的结果都很接近检验样本,但仍可以发现在华南沿海福建地区Cressman产品在36℃以上的高温地区基本没有体现,而在内蒙古地区28~32℃的高温区范围略显不足,在四川陕西交界处32~36℃的高温范围的体现也有所欠缺。
|
图 3 2014年7月13日06时全国气温场(单位:℃)分布:(a)独立检验样本;(b)NLS-3DVar产品;(c)Cressman产品 Fig. 3 Spatial distributions of temperature over China at 0600 UTC 13 July 2014: (a) The independent validation data; (b) NLS-3DVar (Non-linear Least Squares-based on 3DVar) data; (c) Cressman data |
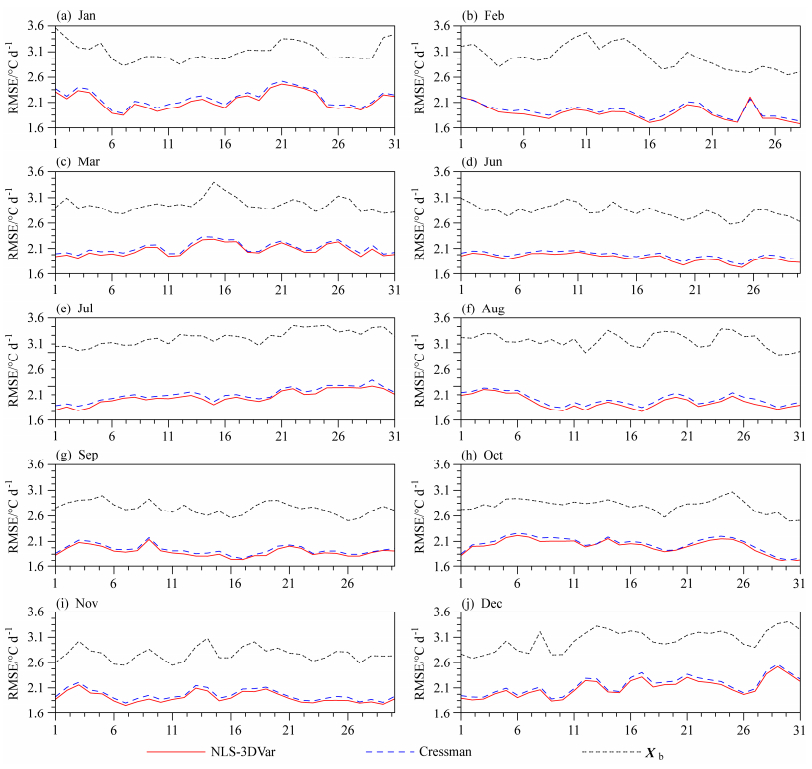
为了进一步明确这两种方法之间的优劣差异,计算了整个时间序列上均方根误差(图 4)和相关系数(图 5)的逐日变化曲线。计算样本为整个中国区域存在的有效独立检验样本。两种产品相比于FNL背景场(图中记为Xb,下同)在均方根误差和相对系数上都有了较为明显的改善,故二者具有可对比性。全年Cressman和NLS-3DVar的产品的均方根误差都比较接近且随时间的变化较为稳定。仍可看出NLS-3DVar产品在全年始终具有较小的均方根误差,Cressman产品的均方根误差总比NLS-3DVar产品大0.05~0.1℃ d–1,7月、8月的差距较其他各月更为明显。图 5相关系数的逐日变化进一步肯定了NLS-3DVar方法的优势。数据显示,NLS-3DVar产品的相关系数最大,基本维持在0.9上下,其次是Cressman产品,略小于NLS-3DVar产品,在6月、7月、8月(图 5d、e、f)的差距较其他各月更为明显。由此可得,相比于Cressman产品,NLS-3DVar产品在全年都有着更小的均方根误差和更大的相关系数。
|
图 4 2014年(4、5月除外)NLS-3DVar产品、Cressman产品和背景场与独立检验样本的均方根误差(单位:℃ d–1)的逐日变化 Fig. 4 Daily variations of RMSEs (units: ℃ d–1) between NLS-3DVar product, Cressman product, background field (Xb) and the independent validation data in 2014 except for April and May |
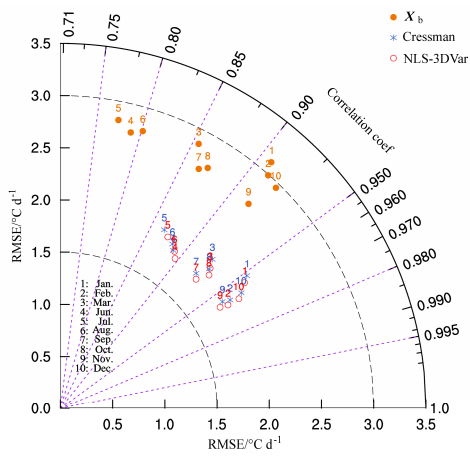
综合均方根误差和相关系数两个变量,我们可以在Taylor图(Taylor,2001)(图 6)中更为直观的通过这两个变量同时对两种产品进行评估。从原点到待评估数据各点的辐射长度是均方根误差(RMSE),待评估点和底边两条射线形成的方位角是相关系数。距离原点和底边越近,效果越好。结合Taylor图中所用数据的数据列表(表 2),可以更为直观和清晰地看出,NLS-3DVar产品在每个月的RMSE和相关系数上都更具优势。NLS-3DVar产品的RMSE与紧随其后的Cressman产品相比,小0.05~0.1℃ d–1。相关系数的统计也表明,NLS-3DVar产品的相关系数在0.88~0.96之间,Cressman产品在0.855~0.955之间,背景场Xb(即NCEP再分析数据)在0.77~0.93之间。
|
图 6 2014年(4、5月除外)NLS-3DVar产品、Cressman产品、背景场Xb与独立检验样本的月平均RMSE(单位:℃ d–1)和相关系数的Taylor图 Fig. 6 Taylor diagram of monthly averaged RMSEs (units: ℃ d–1) and correlation coefficients between NLS-3DVar product, Cressman product, background field Xb and the independent validation data in 2014 except for April and May |
|
|
表 2 2014年(4、5月除外)NLS-3DVar产品、Cressman产品、背景场Xb与独立检验样本的月平均RMSE(单位:℃ d–1) Table 2 Monthly averaged RMSEs (units: ℃ d–1) between NLS-3DVar product, Cressman product, background field Xb and the independent validation data in 2014 except April and May |
综合以上各图表,在融入同样数据的情况下,NLS-3DVar产品优于Cressman产品。与此同时可以看出,Cressman产品的结果与NLS-3DVar产品的结果很接近,无论从RMSE还是相关系数,NLS-3DVar产品都只有微弱的优势,接下来本研究从站点间对比的角度对这两种方法进行进一步的对比检验。
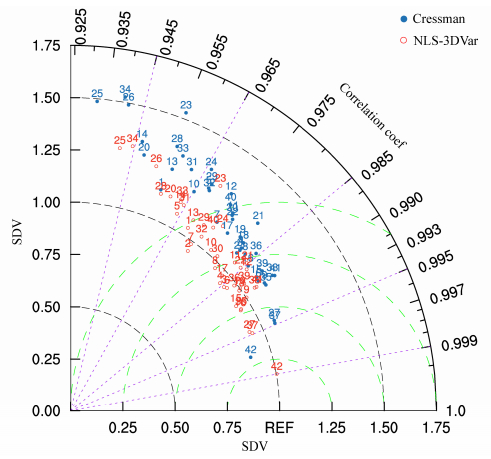
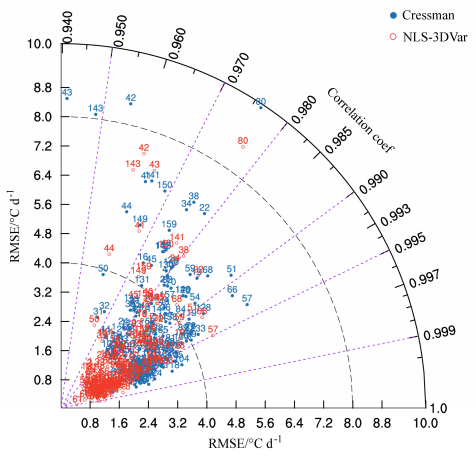
3.2 误差的空间分布前一小节所给出对比的变量都是从整个气温场的平均值出发,展示的都是站点平均值在时间序列下的变化,下面的检验将从站点间逐一的对比展开,纵向比对NLS-3DVar产品和Cressman产品的精度。图 7所示的Taylor图综合考虑规范化的标准差(SDV)和相关系数作为评估指标。用离观测点(图 7中REF点)的距离来表示效果优劣,距离越近,效果越好。作为独立检验样本的18000多个站点,统计显示,NLS-3DVar产品与Cressman产品相比,53.8%的站点的SDV前者比后者更接近1,即与检验样本更相近。图 7中我们筛选了这53.8%的优势站点中,NLS-3Dvar产品与Cressman产品的SDV的差值的绝对值大于0.1的站点,共计42个。NLS-3DVar产品的SDV在0.9~1.3之间,Cressman产品的在0.88~1.55之间,NLS-3DVar产品的站点在更接近1.0线的同时,都具有更大的相关系数,即站点一一对应比较之下,NLS-3DVar的产品更接近REF点,效果更好。同样RMSE的统计也显示,有59.7%的站点NLS-3DVar产品比Cressman产品有更小的均方根误差。图 8中的168个站点选取的是Cressman产品和NLS-3DVar产品的RMSE差值在1.0~1.5℃ d–1之间的独立检验样本站点,NLS-3DVar产品的站点的RMSE大多数分布在0.6~1.6℃ d–1之间,而Cressman产品则在1.5~3.2℃ d–1之间,站点的一一对比可以看出,NLS-3DVar产品的优势站点在具有更小的RMSE同时,有更好的相关系数。
|
图 7 2014年(4、5月除外)NLS-3DVar产品、Cressman产品与独立检验样本的SDV和相关系数的Taylor图 Fig. 7 Taylor diagram of SDV (standard deviation) and correlation coefficients between NLS-3DVar product, Cressman product and the independent validation data in 2014 except for April and May |
|
图 8 Cressman产品、NLS-3DVar产品与独立检验样本的RMSE和相关系数的Taylor图(只给出Cressman产品与NLS-3DVar产品的RMSE差值在1.0~1.5℃ d–1范围的站点) Fig. 8 Taylor diagram of RMSEs and correlation coefficients between NLS-3DVar product, Cressman product and the independent validation data (only those stations with RMSE differences between Cressman and NLS-3DVar products within 1.0~1.5℃ d–1 are counted) |
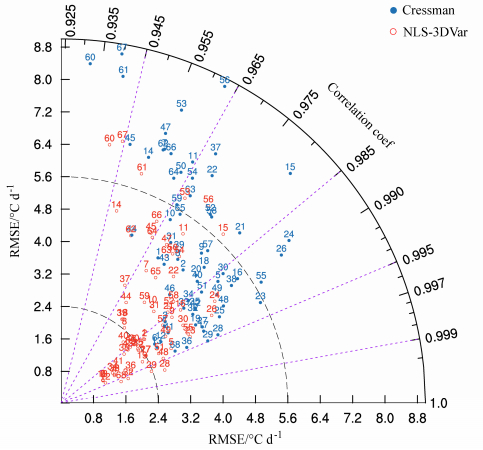
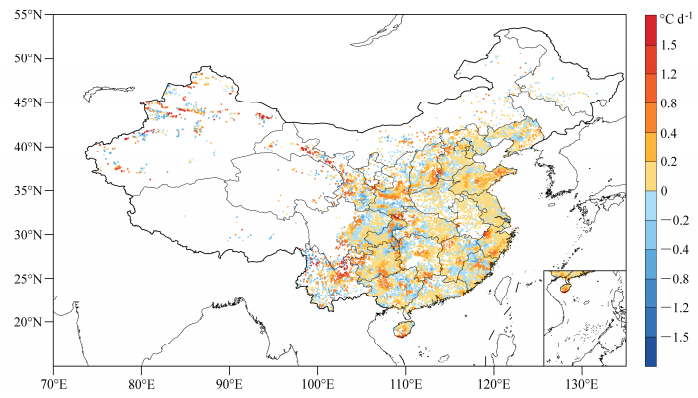
图 9进一步给出了这168个站点的分布状况,主要分布在新疆、甘肃、云南等地区,在江苏和山西也有部分站点。类似地给出了Cressman产品和NLS-3DVar产品的RMSE差值大于1.5℃ d–1的站点(68个站点)的Taylor图(图 10)和站点分布图(图 11)。图 10中可以比较清晰地逐一对比同一站点,NLS-3DVar产品在均方根误差比Cressman产品小1.5的同时,相关系数更大。这68个站点的分布(图 11)同样显示这些站点主要分布在新疆、甘肃地区。同时图 11还给出了所有独立检验站点的RMSE差值。正值表示Cressman产品相比NLS-3DVar产品有更大的RMSE,负值相反。可以看出,整个站点分布以正值居多,且主要在0~0.8之间,1.5以上的站点数也多于–1.5的站点,因此,NLS-3Dvar产品在独立检验样本数据中,均方根误差更小。
|
图 9 Cressman产品、NLS-3DVar产品与独立检验样本的RMSE差值在1.0~1.5℃ d–1范围的站点分布图 Fig. 9 Spatial distribution of stations with RMSE differences within the range of 1–1.5℃ d–1 between Cressman and NLS-3DVar products |
|
图 10 Cressman产品、NLS-3DVar产品与独立检验样本的RMSE和相关系数的Taylor图(只给出Cressman产品与NLS-3DVar产品的RMSE差值 大于1.5℃ d–1的站点) Fig. 10 Taylor diagram of RMSEs and correlation coefficients between NLS-3DVar product, Cressman product and the independent validation data (only those stations with RMSE differences between Cressman and NLS-3DVar products greater than 1.5℃ d–1 are counted) |
|
图 11 Cressman产品、NLS-3DVar产品与独立检验样本的RMSE差值(单位:℃ d–1)分布 Fig. 11 Spatial distribution of RMSE differences (units: ℃ d–1) between Cressman product and NLS-3DVar product |
综合以上分析,从整个气温场的时间序列来看,NLS-3DVar产品相比于原来的FNL背景场有了很大的改善,并且通过与Cressman产品的对比检验,NLS-3DVar产品有更小更稳定的均方根误差和更大的相关系数。尽管与Cressman产品相比NLS-3DVar产品的优势微弱,但是,通过进一步逐个站点的RMSE和相关系数的比较,依然可以看出NLS-3DVar产品具有更高的精度,特别是在新疆、甘肃、云南地区,在山东、江苏、浙江也有比较明显的优势。
4 双重网格下气温数据融合结果评估检验 4.1 统计误差的对比经过前面的讨论,我们已经明确NLS-3DVar产品在精度上的优越性,那么接下来加入多重网格的策略。通过单重网格NLS-3DVar产品和双重网格NLS-3DVar产品的对比,进一步考察观测稀疏化处理给融合产品带来的影响。同时STMAS算法也采用同样分辨率下的双重网格策略,与双重网格的NLS-3DVar产品进行对比。
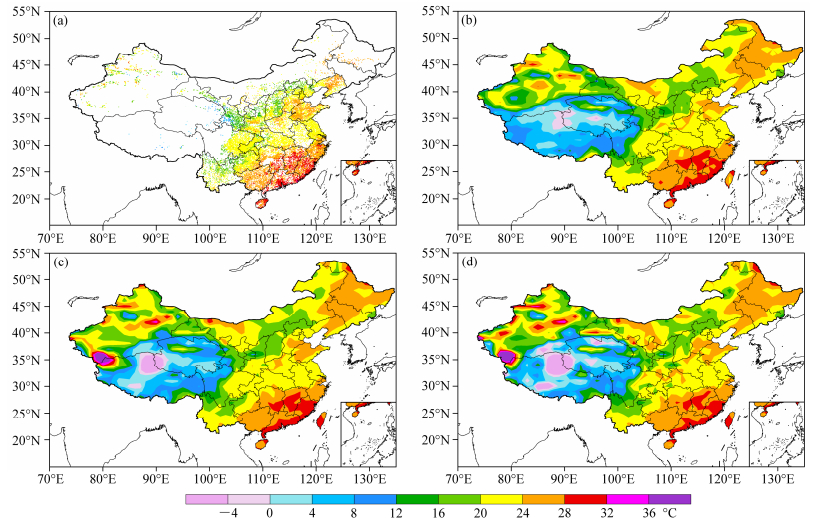
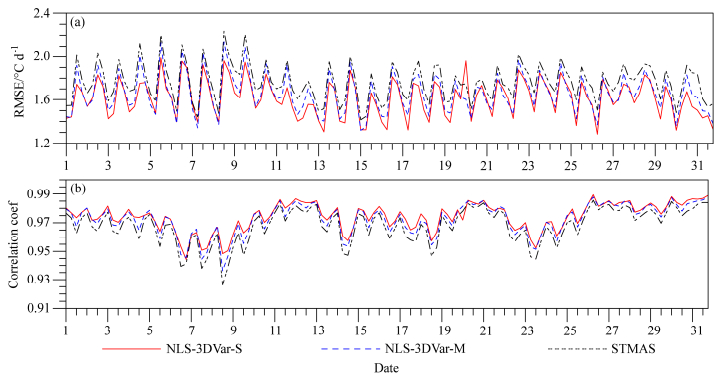
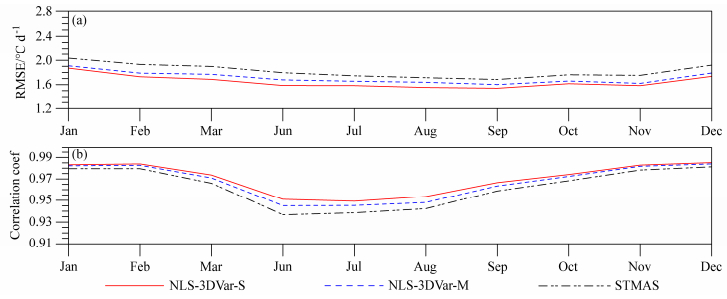
图 12是2014年7月2日00时的气温融合结果。从气温场直观来看,三种产品的结果比较相近,与检验样本相比,从站点丰富的区域来看,三者在气温各个范围都有比较好的表现。2014年10月逐6小时的均方根误差(图 13a)和相关系数(图 13b)显示,单重网格NLS-3DVar产品与双重网格产品的RMSE极为接近,两条曲线几乎呈现重合状态,个别时次二者有0.1~0.2℃ d–1的差异。换言之,通过在NLS-3Dvar方法的同化过程中引入双重网格策略,虽然在同化过程中对观测数据做了稀疏化处理,但是,对产品的精度几乎没什么影响。图 13b中相关系数的展示,也同样证实了单重网格NLS-3DVar产品与双重网格NLS-3DVar产品精度的相近性。而对比双重网格NLS-3DVar产品与STMAS算法产品的均方根误差可以看出,STMAS算法产品的RMSE始终大于双重网格NLS-3DVar产品大约0.1~0.2℃ d–1,且相关系数小于后者0.01~0.02。图 14逐月对RMSE和相关系数做了平均,从全年时间序列和整体平均水平来看,STMAS算法产品无论从均方根误差还是从相关系数来看,都不如双重网格NLS-3DVar产品。由此可见其对于背景误差协方差B和观测误差协方差R的常数比处理的确比较简单和粗糙。从单重网格NLS-3DVar产品和双重网格NLS-3DVar产品的误差对比来看,二者在6、7、8月的差距较其他各月更为明显,但RMSE的差值也只有不到0.1℃ d–1,相关系数亦只相差不足0.01。因此,可认为对于NLS-3DVar方法,双重网格策略的引入,观测稀疏化的处理,对产品精度并没有造成影响。
|
图 12 2014年7月2日00时全国气温场(单位:℃)分布:(a)有效独立检验样本;(b)单重网格NLS-3DVar产品;(c)双重网格NLS-3DVar产品;(d)STMAS算法产品 Fig. 12 Spatial distributions of temperature over China at 0000 UTC 2 July 2014: (a) The independent validation data; (b) single NLS-3DVar product; (c) multigrid NLS-3DVar product; (d) STMAS (Space–Time Multiscale Analysis System) algorithm product |
|
图 13 2014年10月单重网格NLS-3DVar产品、双重网格NLS-3DVar产品、STMAS算法产品与独立检验样本的(a)均方根误差和(b)相关系数 Fig. 13 (a) RMSEs and (b) correlation coefficients between products of single NLS-3DVar, multigrid NLS-3DVar, STMAS algorithm product and the independent validation data during October 2014 |
|
图 14 2014年单重网格NLS-3DVar产品、双重网格NLS-3DVar产品、STMAS算法产品与独立检验样本的逐月平均(a)均方根误差和(b)相关系数 Fig. 14 Monthly mean (a) RMSEs and (b) correlation coefficients between single NLS-3DVar product, multigrid NLS-3DVar product, STMAS algorithm product and the independent validation data in 2014 |
产品精度和计算效率是考证方法优劣的两个重点。图 15是2014年全年平均每月一个同化时次的运行时间统计图。计算均在曙光I620-G20 2U双路机架式服务器上进行,且计算过程均采用串行。柱状图显示,6、7、8月双重网格NLS-3DVar方法单位时次同化运行耗时最少,约为50 s,STMAS算法与之近乎相同,单重网格NLS-3DVar方法在这三个月的耗时虽然在全年来看已经是最短耗时,约为130 s,却仍然是双重网格NLS-3DVar方法计算耗时的2倍多。全年平均数据显示,单重网格NLS-3DVar方法的计算耗时平均为184.16 s,双重网格NLS-2DVar方法为63.45 s,STMAS算法为66.98 s。显然双重网格策略下,NLS-3DVar方法计算耗时更少且优势明显。

|
图 15 2014年单重网格NLS-3DVar方法、双重网格NLS-3DVar方法和STMAS算法逐月平均单位时次同化过程耗时(单位:s)统计 Fig. 15 Statistics of monthly mean time-consuming (units: s) of a single-time assimilation by single NLS-3DVar, multigrid NLS-3DVar, and STMAS algorithm in 2014 |
综合以上结果,NLS-3DVar方法通过引入双重网格策略,在同化过程中对观测数据采取稀疏化处理,最终产品精度在保持原单重网格下产品精度的同时,大幅度地提高了计算效率。与STMAS算法的对比显示,简单的对背景误差协方差和观测误差协方差做常数比处理得到的产品效果不及双重网格NLS-3DVar产品,但计算效率上二者不相上下,也再次证明了多重网格策略在计算效率上的优势。
5 结论与讨论将多重网格策略引入NLS-3DVar方法,并将其应用于气温数据的融合,得到数据空间分辨率1°×1°,时间分辨率为6小时的融合产品。通过和Cressman插值以及STMAS算法的对比,证明采用基于多重网格策略的NLS-3DVar方法得到的气温融合产品具有更高的产品精度和更高的计算效率。首先在单重网格下通过独立性检验,对比了NLS-3DVar产品与气象行业中广泛应用的Cressman插值产品误差的时间分布,并进一步从站点间的误差对比了NLS-3DVar产品和Cressman插值产品的优劣。在此基础上,对NLS-3DVar方法引入了双重网格策略,对比分析了单重网格NLS-3DVar产品、双重网格NLS-3DVar产品和STMAS算法产品的均方根误差、相关系数和运行耗时,全面评估了基于多重网格策略的NLS-3DVar方案得到的气温融合产品。主要结论如下:
(1)单重网格下,独立样本检验表明,在统计误差的时间变化上,NLS-3DVar产品全年具有最高的相关系数和最小的均方根误差,年平均值分别为1.915℃ d–1和0.929,且二者随时间的变化较为稳定,Cressman插值产品略差于NLS-3DVar产品,年平均值分别为1.915℃ d–1和0.929。因此,NLS-3DVar产品相比于Cressman插值产品具有更高的精度。
(2)NLS-3DVar产品和Cressman产品站点间均方根误差和相关系数的对比,进一步肯定了NLS-3DVar方法的优势。独立样本检验中,有53%以上的站点显示NLS-3DVar产品具有更小的均方根误差和更接近1的标准差的同时,具有更高的相关系数。NLS-3DVar的气温融合产品主要在新疆、甘肃、云南、陕西等地相比于Cressman产品有更高的精度。
(3)双重网格NLS-3DVar气温融合产品相较于原来的单重网格产品,精度基本没有发生明显的变化,只在个别时次略差于单重网格产品,而与同样是双重网格的STMAS算法的产品对比,均方根误差和相关系数都明显处于优势,也因此说明STMAS算法中对于背景误差协方差B和观测误差协方差R的常数比处理比较粗糙。通过单位时次同化耗时的进一步对比,充分体现了双重网格NLS-3DVar方法的优势。全年平均数据显示,单重网格NLS-3DVar方法的计算耗时平均为184.16 s,双重网格NLS-2DVar方法为63.45 s,STMAS算法为66.98 s。双重网格NLS-3DVar方法在维持原本产品精度保持优势的前提下,大幅度地提高了计算效率,节省运行时间。
通过以上研究,基于多重网格策略的NLS-3DVar方法应用于气温数据的融合产品在精度和计算效率上的双重优势充分证明了该方案的优越性,其基于非线性的最小二乘迭代算法,只通过很少的迭代次数,便得到了比Cressman插值和STMAS算法更好的结果。
| [] | Chen D L, Ou T H, Gong L B, et al. 2010. Spatial interpolation of daily precipitation in China:1951-2005[J]. Advances in Atmospheric Sciences, 27(6): 1221–1232. DOI:10.1007/s00376-010-9151-y |
| [] | Cressman G P. 1959. An operational objective analysis system[J]. Mon. Wea. Rev., 87(10): 367–374. DOI:10.1175/1520-0493(1959)087<0367:AOOAS>2.0.CO;2 |
| [] | Dennis J E Jr, Schnabel R B. 1996. Numerical Methods for Unconstrained Optimization and Nonlinear Equations (Classics in Applied Mathematics)[M]. Philadelphia:SIAM, 378pp. |
| [] | Evensen G. 2004. Sampling strategies and square root analysis schemes for the EnKF[J]. Ocean Dynamics, 54(6): 539–560. DOI:10.1007/s10236-004-0099-2 |
| [] | 冯锦明, 赵天保, 张英娟. 2004. 基于台站降水资料对不同空间内插方法的比较[J]. 气候与环境研究, 9(2): 261–277. Feng Jinming, Zhao Tianbao, Zhang Yingjuan. 2004. Intercomparison of spatial interpolation based on observed precipitation data[J]. Climatic and Environmental Research (in Chinese), 9(2): 261–277. DOI:10.3969/j.issn.1006-9585.2004.02.004 |
| [] | Li W, Xie Y F, Deng S M, et al. 2010. Application of the multigrid method to the two-dimensional Doppler radar radial velocity data assimilation[J]. J. Atmos. Oceanic Technol., 27(2): 319–332. DOI:10.1175/2009JTECHA1271.1 |
| [] | Li W, Xie Y F, He Z J, et al. 2008. Application of the multigrid data assimilation scheme to the China Seas' temperature forecast[J]. J. Atmos. Oceanic Technol., 25(11): 2106–2116. DOI:10.1175/2008JTECHO510.1 |
| [] | Li W, Xie Y F, Han G J. 2013. A theoretical study of the multigrid three-dimensional variational data assimilation scheme using a simple bilinear interpolation algorithm[J]. Acta Oceanologica Sinica, 32(3): 80–87. DOI:10.1007/s13131-013-0292-6 |
| [] | Liu C S, Xiao Q N, Wang B. 2009. An ensemble-based four-dimensional variational data assimilation scheme. Part Ⅱ:Observing system simulation experiments with advanced research WRF (ARW)[J]. Mon. Wea. Rev., 137(5): 1687–1704. DOI:10.1175/2008MWR2699.1 |
| [] | 苗春生, 程远, 王坚红, 等. 2015. 中国风云卫星与海洋卫星近海SST资料融合技术及应用研究[J]. 地球科学进展, 30(10): 1127–1143. Miao Chunsheng, Cheng Yuan, Wang Jianhong, et al. 2015. Data fusion of offshore SST from China FY and HY2 satellites and its application[J]. Advances in Earth Science (in Chinese), 30(10): 1127–1143. DOI:10.11867/j.issn.1001-8166.2015.10.1127 |
| [] | 任芝花, 张志富, 孙超, 等. 2015. 全国自动气象站实时观测资料三级质量控制系统研制[J]. 气象, 41(10): 1268–1277. Ren Zhihua, Zhang Zhifu, Sun Chao, et al. 2015. Development of three-step quality control system of real-time observation data from AWS in China[J]. Meteorological Monthly (in Chinese), 41(10): 1268–1277. DOI:10.7519/j.issn.1000-0526.2015.10.010 |
| [] | 申思. 2015. 降维投影四维变分同化方法的改进及在GRAPES全球模式中的初步应用[D]. 中国科学院大学博士学位论文. Shen Si. 2015. Improvements for dimension-reduced projection 4DVar and its preliminary application in GRAPES-GFS[D]. Ph. D. dissertation (in Chinese), University of Chinese Academy of Sciences. |
| [] | Taylor K E. 2001. Summarizing multiple aspects of model performance in a single diagram[J]. J. Geophys. Res., 106(D7): 7183–7192. DOI:10.1029/2000JA002008 |
| [] | Tian X J, Feng X B. 2015. A non-linear least squares enhanced POD-4DVar algorithm for data assimilation[J]. Tellus A, 67: 25340. DOI:10.3402/tellusa.v67.25340 |
| [] | Tian X J, Feng X B, Zhang H Q, et al. 2016. An enhanced ensemble-based method for computing CNOPs using an efficient localization implementation scheme and a two-step optimization strategy:Formulation and preliminary tests[J]. Quart. J. Roy. Meteor. Soc., 142(695): 1007–1016. DOI:10.1002/qj.2703 |
| [] | Tian X J, Xie Z H, Sun Q. 2011. A POD-based ensemble four-dimensional variational assimilation method[J]. Tellus A, 63(4): 805–816. DOI:10.1111/j.1600-0870.2011.00529.x |
| [] | Wang B, Liu J J, Wang S D, et al. 2010. An economical approach to four-dimensional variational data assimilation[J]. Advances in Atmospheric Sciences, 27(4): 715–727. DOI:10.1007/s00376-009-9122-3 |
| [] | Xie Y, Koch S, McGinley J, et al. 2011. A space-time multiscale analysis system:A sequential variational analysis approach[J]. Mon. Wea. Rev., 139(4): 1224–1240. DOI:10.1175/2010MWR3338.1 |
| [] | Xie Y, Koch S E, McGinley J A, et al. 2005. A sequential variational analysis approach for mesoscale data assimilation[C]//Proceedings of the 21st Conference on Weather Analysis and Forecasting/17th Conference on Numerical Weather Prediction. Washington, D. C.:American Meteor Society. |
| [] | 熊秋芬, 黄玫, 熊敏诠, 等. 2011. 基于国家气象观测站逐日降水格点数据的交叉检验误差分析[J]. 高原气象, 30(6): 1615–1625. Xiong Qiufen, Huang Mei, Xiong Minquan, et al. 2011. Cross-validation error analysis of daily gridded precipitation based on China meteorological observation[J]. Plateau Meteorology (in Chinese), 30(6): 1615–1625. |
| [] | 宇婧婧, 沈艳, 潘旸, 等. 2015. 中国区域逐日融合降水数据集与国际降水产品的对比评估[J]. 气象学报, 73(2): 394–410. Yu Jingjing, Shen Yan, Pan Yang, et al. 2015. Comparative assessment between the daily merged precipitation dataset over China and the world's popular counterparts[J]. Acta Meterorologica Sinica (in Chinese), 73(2): 394–410. DOI:10.11676/qxxb2015.033 |
 2017, Vol. 22
2017, Vol. 22



