2 中国海洋大学物理海洋实验室, 山东省高校海洋-大气相互作用与气候重点实验室 山东青岛 266100;
3 中国科学院南海海洋研究所热带海洋环境国家重点实验室, 广州 510000
2 Physical Oceanography Laboratory, The Key Laboratory of Ocean-Atmosphere Interaction and Climate in Universities of Shandong, Ocean University of China, Qingdao Shandong 266100;
3 State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510000
风暴轴(Storm Track)是指天气尺度(2.5~6 d)上大气瞬变扰动最活跃的区域,对应于中高纬度地面气旋和反气旋路径。目前,有两种定义方法,一类是通过统计中纬度气旋、反气旋发生的频率,追踪其移动路径来确定风暴轴的强度和位置演变(Overland and Pease, 1982),另一类为Blackmon(1976)提出的将天气尺度(2.5~6 d)瞬变扰动方差的极大值带定义为风暴轴。北半球存在两大风暴轴,分别位于太平洋和大西洋上,且冬季强夏季弱(邓兴秀和孙照渤,1994)。风暴轴三维分布图显示,风暴轴在对流层高低空均存在,能量集中在对流层中上层,低层风暴轴入口处对应涡旋运动产生(Hoskins et al., 1983)。
自从Blackmon(1976)用滤波方差表征风暴轴以来,有关风暴轴的内部维持机制上也有更深入的研究:风暴轴区域的扰动以纬向波列形式向东传播(Blackmon et al., 1984a, 1984b;Hakim,2002;Simmons and Hoskins, 1978),斜压波对于定常存在的阻塞结构的维持和发展起到重要作用(Illari and Marshall, 1983;Nakamura et al., 1997),因此能量形成准静止的风暴轴(Orlanski,1998),故斜压不稳定常常被视为中纬度瞬变波发展的一个主要原因(Frederiksen and Frederiksen, 1993;Lee,1995)。自从将涡动动能(Eddy Kinetic Energy,EKE)方程运用于风暴轴能量研究以来(Orlanski and Katzfey, 1990;Orlanski and Gross, 1999),有大量关于风暴轴能量的收支研究立足于EKE方程的分解:Jiang(2013)通过分解EKE方程,得到对流层中下层斜压转换项为风暴轴EKE的主要来源,而正压转换项损耗风暴轴EKE。然而有研究通过分析风暴轴内部EKE收支,弱化了斜压波在风暴轴局地维持中的作用,而强调了“下游频散效应”在斜压不稳定较弱的区域涡旋维持和发展的重要性,同时证明非地转通量的辐合辐散能够决定斜压和正压之间的转换(Chang and Orlanski, 1993;孙照渤和朱伟军,2000)。
在北大西洋风暴轴不同区域的EKE对比上,大量研究表明风暴轴东、西两端的结构存在明显差异,其西端为强的斜压性结构,到了东端逐渐转变为相当正压结构(Lau,1978;Hoskins and Valdes, 1990;朱伟军和孙照渤,1999)。而对北大西洋风暴轴来说,其存在明显的东进—西退变化,当风暴轴向东扩展时,斜压转换项导致风暴轴上游EKE增强,而非地转位势通量导致风暴轴下游EKE增强,向西收缩时,能量转化则相反(曾鼎文等,2015)。然而前人关于风暴轴维持机制的研究都是将其看作一个整体,而本文立足于EKE方程分解的方法,将北大西洋上、下层风暴轴分开讨论,对比正、斜压能量转换及能量频散等大气内部动力过程在北大西洋风暴轴高低空维持机制中所起的作用。
本文首先给出北大西洋风暴轴高低空气候态和第一空间分布型,然后运用EKE变化方程,诊断正、斜压能量转换及能量频散等大气内部动力过程在北大西洋风暴轴高低空维持机制中所起的作用。
2 资料和方法文中使用的资料为1979年1月至2013年12月NECP逐日和逐月的位势高度场、风场和温度场资料,时间长度为35年,水平分辨率为2.5°(纬度)×2.5°(经度),本文分析了1000、850、700、500、300和200 hPa六层数据。
本文采用谐波滤波技术,从NCEP逐日位势高度场资料中滤出2.5~6 d的天气尺度瞬变扰动,并计算逐月方差,来代表该年冬季天气尺度扰动的空间分布,也即Blackmon(1976)所定义的风暴轴。对风场和温度场也进行2.5~6 d滤波,用来计算EKE变化方程中的各项。
本文立足于冬季北半球风暴轴,取平均强度最强的11、12、1月为风暴轴的冬季(Bengtsson et al., 2006)。文中主要采用了经验正交函数分解(Empirical Orthogonal Function,EOF)分解技术探讨北半球风暴轴的空间异常型和时间演变特征。
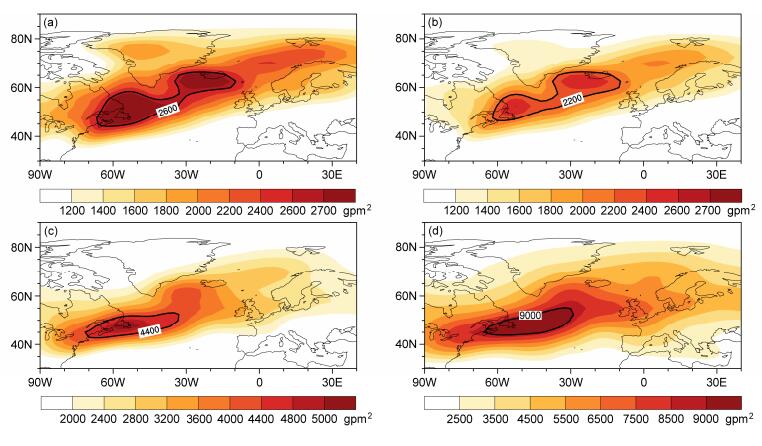
3 北大西洋风暴轴高低空空间分布差异 3.1 北大西洋风暴轴气候态分布本文的风暴轴用2.5~6 d滤波后的位势高度场方差极大值带表示,图 1为冬季平均的北大西洋风暴轴(North Atlantic Storm Track)在为对流层低层(1000 hPa、850 hPa)和对流层上层(500 hPa、300 hPa)的水平分布图情况。从图 1a可以看出,在大西洋低层1000 hPa风暴轴的极大值带东部北抬,呈东北—西南走势,且暴轴存在两个极大值中心(大于2600 gpm2的区域),分别位于北美东岸(45°N,60°W)和冰岛(60°N,20°W)附近。同样,虽然850 hPa风暴轴整体强度有所减弱,两个极大值的结构依然存在(图 1b),500 hPa的情况呢?但是在对流层上层300 hPa,风暴轴逐渐变为一致的东西向纬向拉长型,冰岛中心减弱消失,北美东部(45°N,60°W)中心强度随着高度的增加(图 1c、1d)。因此,可以看出,气候态风暴轴上层和下层的结构不同,除了同上层一致的北美中心外,下层在冰岛附近还有一个中心。在此外,注意到1000 hPa的风暴轴强度强于850 hPa,这表明大气低层与陆地(海洋)交界处,可能向风暴轴提供能量(Deser et al., 2000)。
|
图 1 1979~2013年35年冬季平均北大西洋风暴轴强度分布:(a)1000 hPa;(b)850 hPa;(c)500 hPa;(d)300 hPa Fig. 1 35 years mean (1979−2013) winter storm track strength in the Northern Hemisphere: (a) 1000 hPa; (b) 850 hPa; (c) 500 hPa; (d) 300 hPa |
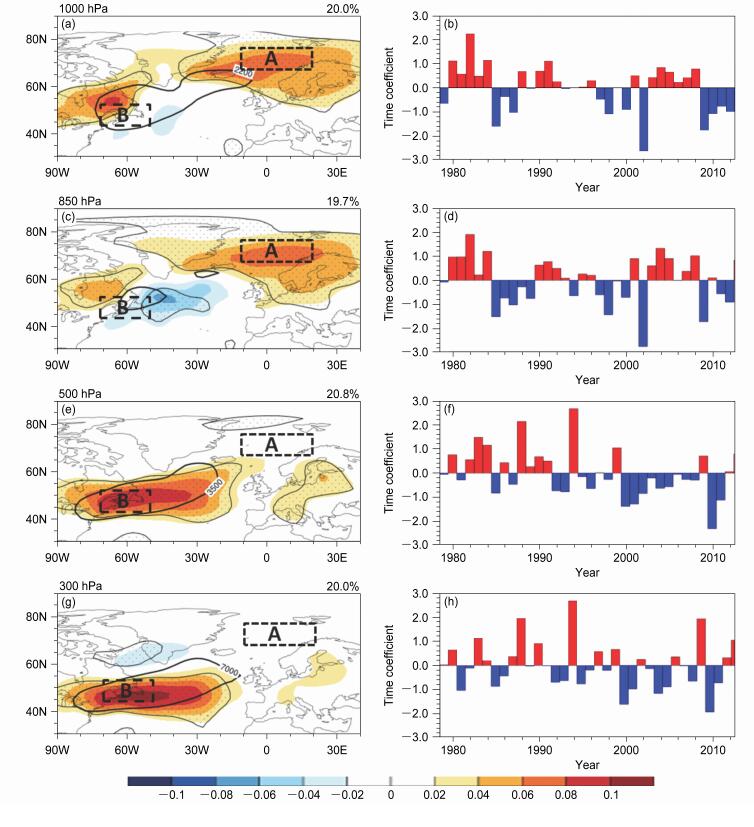
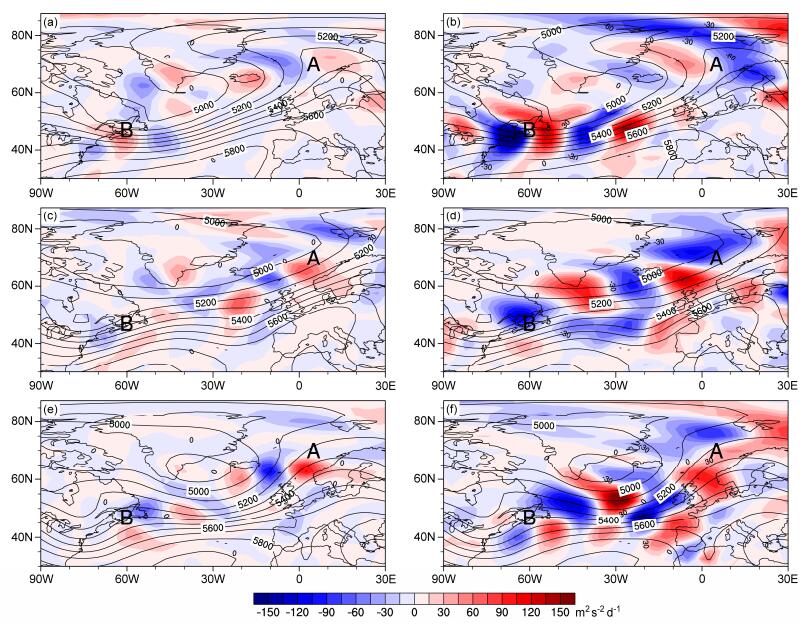
接下来针对北大西洋风暴轴做EOF分解。图 2是各高度层第一模态对应的风暴轴空间分布和时间序列,打点区域表示将EOF第一模态的时间序列回归到风暴轴异常场后的相关性通过95% t检验区域,表明该模态能够表征风暴轴主要分布特点。由图 2可知,同气候态分布一样,整个对流层上层和下层反映了不同的空间分布特点。具体来说,对流层的低层(1000 hPa和850 hPa)(图 2a、2c)空间分布型相似,即风暴轴主体位于气候态风暴轴位置(黑色等值线)的下游——格陵兰岛以东,我们将该区域极大值带定义为A区域(黑色虚线框:65°N~75°N,10°W~20°E),该区域较气候态冰岛中心偏北。
|
图 2 风暴轴各层EOF分解的第一模态空间分布(左列)以及对应的标准化后的时间系数(PC1,右列):(a、b)1000 hPa;(c、d)850 hPa;(e、f)500 hPa;(g、h)300 hPa。左列图右上角百分数表示方差贡献,图中打点区域表示将PC1回归到风暴轴异常场上通过95% t检验的区域,“A”表示低层风暴轴第一空间分布型的主体位置,“B”表示上层风暴轴第一空间分布型的主体位置,下同,黑色虚线方框代表风暴轴中心的周边区域 Fig. 2 Spatial pattern (left column) and time coefficients (right column) of the first leading mode of storm track at (a, b) 1000 hPa, (c, d) 850 hPa, (e, f) 500 hPa, and (g, h) 300 hPa. In a, c, e, and g, the percentage represents the percent variance explained by the mode; dotted areas indicate the regression coefficients of the first leading mode on the storm track anomaly pass the 95% confidence level by Student-t test; "A" is the location of the lower layer storm track in its first EOF (Empirical Orthogonal Function) pattern, "B" is the location of the upper layer storm track in its first EOF pattern, the same blow; the black boxes indicate the central areas |
同样,对流层上层(500 hPa和300 hPa)的空间分布相似,和低层相反,上层的主体位于气候态的上游——北美东部,我们将该区域极大值带定义为B区域(黑色虚线框:42°N~52°N、50°W~70°W)。本文的分区也对应着Lau(1978)对风暴轴的分区,大西洋区(30°W~70°W)和欧洲区(20°W~30°E)。
结合时间序列,对不同层数第一模态对应时间系数(PC1)分别做相关(表 1),发现低层1000 hPa和850 hPa PC1的相关系数高达0.92,通过95% t检验,表现为显著相关,因此,风暴轴低层1000 hPa和850 hPa的空间分布和时间变化都是一致的。同样,上层500 hPa和300 hPa PC1显著相关,相关系数为0.87,即说明风暴轴上层500 hPa和300 hPa时空变化一致。然而高、低空PC1间相关系数较低,且低层1000 hPa、850 hPa与高空500 hPa、300 hPa间的相关性都不显著(表 1),表明风暴轴上层和下层不仅分布空间分布型存在巨大差异,其时间变化也不同。综上所述,同气候态分析结果一致,EOF所表征的风暴轴主要分布型也反映出上层和下层的显著差异,且下层中心位于格陵兰岛以东,而上层中心位于北美东部。本文接下来将上、下层分开讨论其能量转化,从而探讨风暴轴上、下层分布不同的原因。
|
|
表 1 风暴轴各层EOF第一模态对应时间系数的相关系数 Table 1 Correlation coefficient between the PC1 at different levels |
本节将从涡动动能能量分析角度,从涡动动能方程出发,通过诊断分析平均动能、平均位能、涡动动能和涡度位能之间的转换,讨论高低空风暴轴能量演变过程的差异。
Orlanski and Katzfey(1990)根据动力学方程提出的涡动动能
| $ \begin{array}{*{20}{l}} {\frac{{\partial {K_{\rm{e}}}}}{{\partial t}} + \left( {{\mathit{\boldsymbol{V}}_{\rm{m}}} \cdot \nabla {K_{\rm{e}}} + {\omega _{\rm{m}}}\frac{{\partial {K_{\rm{e}}}}}{{\partial p}}} \right) + \left( {\mathit{\boldsymbol{v'}} \cdot \nabla {K_{\rm{e}}} + \omega '\frac{{\partial {K_{\rm{e}}}}}{{\partial p}}} \right) = }\\ {\left[ { - \nabla \cdot \left( {\mathit{\boldsymbol{v'}}\Phi '} \right) - \omega '\alpha '} \right] - \left[ {\mathit{\boldsymbol{v'}} \cdot \left( {\mathit{\boldsymbol{v'}}\nabla {\mathit{\boldsymbol{V}}_{\rm{m}}} + \omega '\frac{{\partial {\mathit{\boldsymbol{V}}_{\rm{m}}}}}{{\partial p}}} \right)} \right] + }\\ {\left[ {\mathit{\boldsymbol{v'}} \cdot \overline {\left( {\mathit{\boldsymbol{v'}}\nabla \mathit{\boldsymbol{v'}} + \omega '\frac{{\partial \mathit{\boldsymbol{v'}}}}{{\partial p}}} \right)} } \right] - {d_{{\rm{isse}}}} + \mathit{\boldsymbol{v'}} \cdot {F_0},} \end{array} $ | (1) |
其中,
公式(1)左端分别为涡动动能的局地变化项、涡动动能的平均平流项和涡动平流项。右端第一项为涡旋引起的气压变化,其中,
同样,孙照渤和朱伟军(2000)根据热力学方程得到涡动有效位能
| $ $\begin{array}{l} \frac{{\partial {A_{\rm{e}}}}}{{\partial t}} + {\mathit{\boldsymbol{V}}_m} \cdot \nabla {A_{\rm{e}}} + \mathit{\boldsymbol{v}}' \cdot \nabla {A_{\rm{e}}} = \omega '\alpha ' - \frac{1}{e}\left({\frac{{\partial \mathit{\Phi} '}}{{\partial p}}} \right)\mathit{\boldsymbol{v}}' \cdot {\rm{ }}\\ \nabla \left({\frac{{\partial {\mathit{\Phi} _{\rm{m}}}}}{{\partial p}}} \right) - \frac{{R{Q_{\rm{e}}}}}{{e{c_p}{P_{\rm{e}}}}}\left({\frac{{\partial \mathit{\Phi} '}}{{\partial p}}} \right) + \frac{1}{e}\left({\frac{{\partial \mathit{\Phi} '}}{{\partial p}}} \right)\overline {\left[ {\mathit{\boldsymbol{v}}' \cdot \nabla \left({\frac{{\partial \mathit{\Phi} '}}{{\partial p}}} \right)} \right]} {\rm{ }}, \end{array}$ $ | (2) |
其中,
(1)涡动非地转位势通量散度项
(2)涡动有效位能与涡动动能之间的斜压转换项
(3)平均动能与涡动动能的正压转换项
| $ C({K_{\rm{m}}}, {K_{\rm{e}}}) = - \left[ {v' \cdot \left({v'\nabla {\mathit{\boldsymbol{V}}_m} + \omega '\frac{{\partial {\mathit{\boldsymbol{V}}_{\rm{m}}}}}{{\partial p}}} \right)} \right] $ | (3) |
(4)时间平均有效位能与涡动有效位能之间的斜压转换项
| $ C({A_{\rm{m}}}, {A_{\rm{e}}}) = - \frac{1}{e}(\frac{{\partial \mathit{\Phi} '}}{{\partial p}})\mathit{\boldsymbol{v}}' \cdot \nabla (\frac{{\partial {\mathit{\Phi} _{\rm{m}}}}}{{\partial p}}) $ | (4) |
由于本文分析北大西洋风暴轴高低空能量,故将对流层低层(1000~700 hPa)和高层(500~200 hPa)分别做垂直平均:
| $ \hat A = \frac{1}{{({p_{\rm{S}}} - {p_{\rm{T}}})}}\int_{{p_{\rm{T}}}}^{{p_{\rm{S}}}} {A{\rm{d}}p} $ | (5) |
其中,
接下来,本文对比分析北大西洋风暴轴高低空,涡动动能Ke的分布,以及影响涡动动能变化的4个转换项:时间平均有效位能与涡动有效位能之间的斜压转换项
考虑到月平均后的能量演变可能对具体涡动的能量演变有所削弱,因为扰动波列为天气尺度,即风暴轴为2.5~6 d天气尺度的扰动,而能量的传播也为天气尺度的波列形式,因此,本文分析上、下层风暴轴能量演变采用个例分析的方法(孙照渤和朱伟军,2000)。选取时段为2013年12月13~18日,该时段为一次北大西洋扰动向极移动过程。
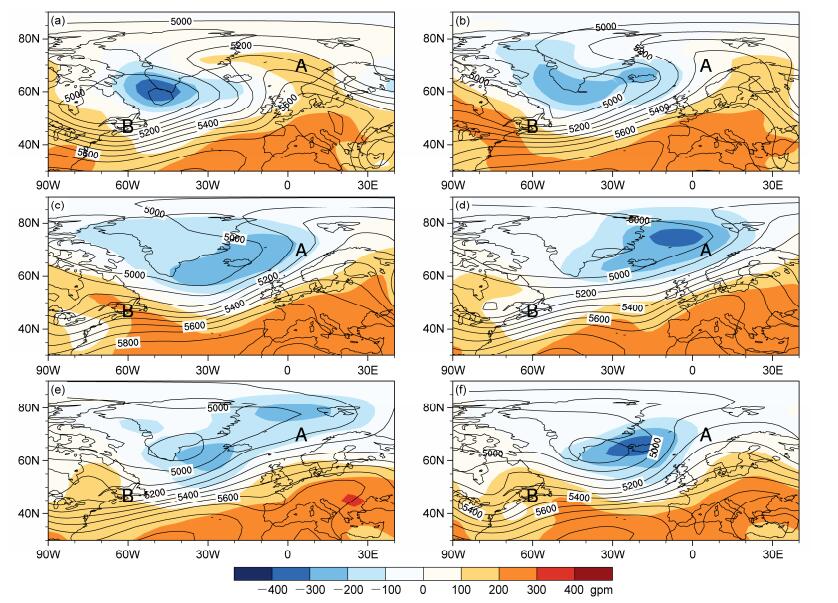
图 3展示了2013年12月13~18日,一个地面低压扰动的向极移动过程:自13日(图 3a)大西洋上空500 hPa出现大槽,槽的中心地面形成低压扰动,此时该扰动正好位于B区域附近。随着高空槽转横,该扰动从格陵兰岛以南(图 3a)向北极移动至格陵兰岛以东的极圈附近(图 3d、3e、3f),此时正好位于A区域附近。接下来的分析,仅选取12月14、16、18日,分别代表扰动从B区域(14日)移动至A区域(16日)再回撤(18日)的过程。并对流层上层500~200 hPa和下层1000~700 hPa分别垂直加权平均,代表风暴轴上层和下层的能量总和。
|
图 3 2013年12月13~18日一个地面低压扰动的发展演变过程500 hPa位势高度场(等值线,单位:gpm)和1000 hPa位势高度场(填色)的空间分布:(a)13日;(b)14日;(c)15日;(d)16日;(e)17日;(f)18日 Fig. 3 Evolution of a cyclonic disturbance during 13−18 December 2013: (a) 13 December; (b) 14 December; (c) 15 December; (d) 16 December; (e) 17 December; (f) 18 December. Contours show 500-hPa geopotential height distribution, which describes the troughs and ridges in the middle troposphere. Shaded is 1000-hPa geopotential height distribution, which illustrates the cyclonic disturbance near the surface |
该过程的涡动动能分布图(图 4)极大值位置与风暴轴上、下层分布有很好的对应关系(图 2)(Luo et al., 2011;朱伟军和孙照渤,2001)。14日(图 4a、4b),风暴轴上层的EKE极大值区域位于风暴轴上游,北美东部,即之前提到的B区附近。随着高空槽的移动,该极大值区域向东北移动,16日(图 4c、4d),移至风暴轴下游,即之前提到的A区附近。

|
图 4 2013年12月(a、b)14日、(c、d)16日、(e、f)18日涡动动能Ke(单位:m2 s−2 d−1,阴影部分)在风暴轴上、下层的分布情况,叠加500 hPa位势高度场(实线,单位:gpm)、1000 hPa位势高度场(虚线,单位:gpm):(a、c、e)对流层低层1000~700 hPa平均;(b、d、f)对流层上层500~200 hPa平均 Fig. 4 Distributions of eddy kinetic energy Ke (shaded, units: m2 s−2 d−1) superimposed on geopotential height at 500 hPa (solid contours, units: gpm) and 1000 hPa (dashed contours, units: gpm) during the evolution of a transverse trough: (a, c, e) Averaged in the lower troposphere (1000−700 hPa); (b, d, f) averaged in the upper layer of troposphere (500−200 hPa) |
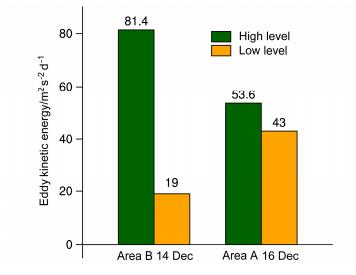
比较扰动移动过程中,B、A区域平均EKE值的变化,当扰动在风暴轴上游B区时(图 4a、4b),该区上层EKE明显大于下层,区域平均EKE值见图 5;当扰动移动至风暴轴下游A区时(图 4c、4d),下层EKE增加,上层EKE减少,两区域平均EKE值相差不大(图 5)。这也说明了,上层EKE中在B区,而下层EKE中心在A区,进一步说明了上一节得出的结论:风暴轴上层和下层的主体位置分别在B区和A区。
|
图 5 2013年12月14日B区和12月16日A区涡动动能的区域平均值 Fig. 5 Averaged EKE in area B on 14 December 2013 and area A on 16 Deccember 2013 |
接下来,从各转换项能量的角度,分析构成涡动动能转化方程中的各项,从而解释该扰动过程中,高低空天气尺度涡动动能(EKE)极大值分布出现显著差异的原因。
由涡动动能和涡动方程(1)和有效位能转化方程(2)得,涡动能量主要来源于:斜压转换项
|
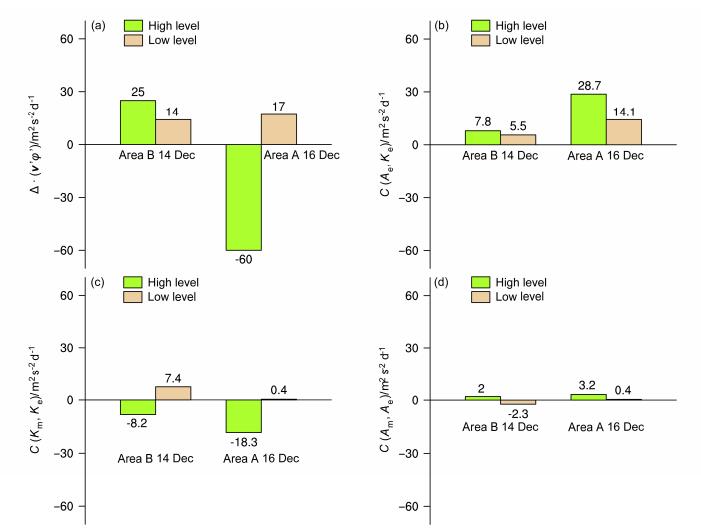
图 6 2013年12月14日B区和12月16日A区4个转换项的区域平均值:(a) |
|
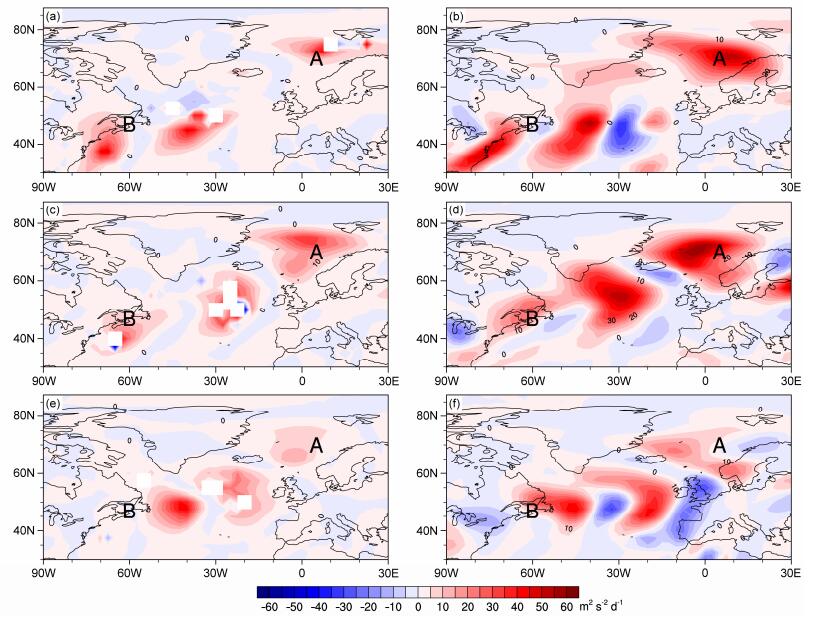
图 7 2013年12月(a、b)14日、(c、d)16日、(e、f)18日平均有效位能向涡动有效位能的斜压转换项 |
|
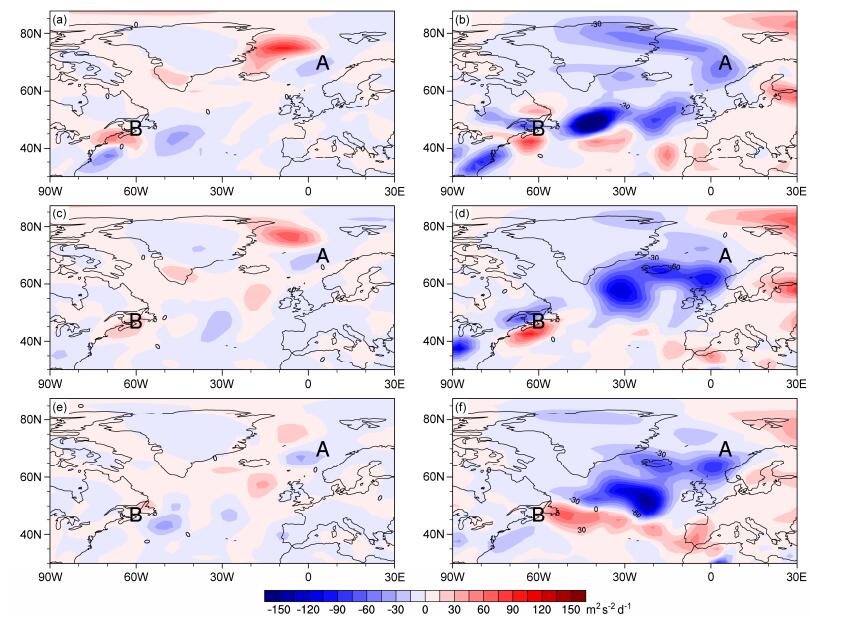
图 8 同图 7,但为平均动能向涡动动能的的正压转换项 |
|
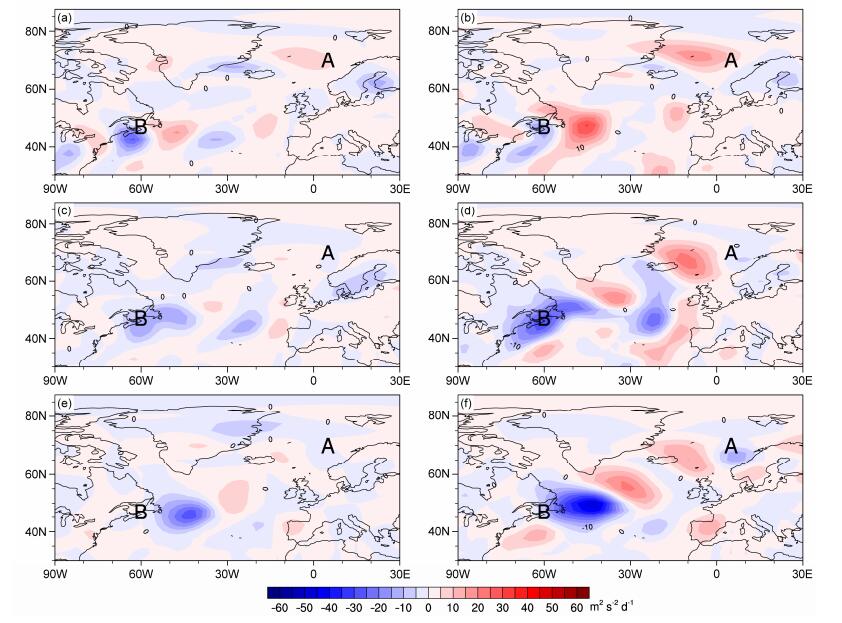
图 9 同图 7,但为涡动有效位能与涡动动能的斜压转换项 |
图 8为平均动能向涡动动能的的正压转换项
图 10表明非地转位势通量散度
|
图 10 2013年12月(a、b)14日、(c、d)16日、(e、f)18日涡动非地转位势通量散度项 |
然而,正因为散度项是以波列的形式传播,且从图 10可以看出周期短,传播快,使得此项对总能量的贡献不稳定,出现较大的每日差异,对于同一天,A、B区域处于波列不同位相时,将会导致该项对EKE的相反贡献,如14日B区位于波动正位相,通量散度
综上所述,就上、下层对比而言,平均动能向涡动动能的正压转换能量
就扰动极大值空间分布而言,本文扰动发展过程中,风暴轴下层中心出现在A区的原因为:斜压转换
本文通过对不同高度位势高度场2.5~6天滤波,得出其方差极大值带,用以表示风暴轴的位置。前冬时期(11月、12月、1月)气候态平均后的北大西洋风暴轴低层表现为东部北抬,呈东北—西南分布,有两个极大值中心,分别位于北美东岸(45°N、60°W)和冰岛(65°N、20°W)附近。之后,对北大西洋风暴轴不同层分别做EOF分解,发现上、下层空间分布型中,风暴轴位置差异巨大。对流层的低层(1000 hPa和850 hPa)的中心靠近极地(B区),而对流层上层(500 hPa和300 hPa)的中心靠近北美沿岸(A区)。结合时间序列,对不同层数的PC1分别做相关,发现低层1000 hPa和850 hPa PC1表现为显著相关,上层500 hPa和300 hPa PC1显著相关。说明风暴轴低层和上层分别为整层一致的变化,且上、下两层变化差异巨大。
接下来,从涡动动能方程出发,通过诊断分析平均能量与涡动能量之间的转换,不同类型涡动能量之间的转换和涡动非地转位势通量散度项,解释天气尺度扰动能量在高低空分布不一致的原因。考虑到月平均后的能量演变可能对具体涡动的能量演变有所削弱,文中选择一次北大西洋扰动向极移动过程进行分析。结果表明:该扰动的移动与500 hPa高空槽的移动有关,其位置对应高低空涡动能量极大值区域。分析构成涡动动能转化方程中的各项,得到:(1)上、下层扰动动能的主要来源于平均有效位能向涡动有效位能的斜压转换项
前人大量研究和得到广泛认可的风暴轴维持机制为正压和斜压转换项,以及非地转位势通量项,平流项会被忽略。因此,本文的能量分析侧重于正压和斜压转换项。此外,本文仅对一个典型个例开展了分析,今后将开展更多的个例研究,并对多个个例进行比较、合成分析。
| [] | Bengtsson L, Hodges K I, Roeckner E. 2006. Storm tracks and climate change[J]. J. Climate, 19(15): 3518–3543. DOI:10.1175/JCLI3815.1 |
| [] | Blackmon M, L. 1976. A climatological spectral study of the 500 mb geopotential height of the Northern Hemisphere[J]. J. Atmos. Sci., 33(1): 1607–1623. DOI:10.1175/1520-0469(1976)033<1607:ACSSOT>2.0.CO;2 |
| [] | Blackmon M L, Lee Y H, Wallace J M. 1984a. Horizontal structure of 500 mb height fluctuations with long, intermediate and short time scales[J]. J. Atmos. Sci., 41(6): 961–980. DOI:10.1175/1520-0469(1984)041<0961:HSOMHF>2.0.CO;2 |
| [] | Blackmon M L, Lee Y H, Wallace J M, et al. 1984b. Time variation of 500 mb height fluctuations with long intermediate and short time scales as deduced from lag-correlation statistics[J]. J. Atmos. Sci., 41(6): 981–991. DOI:10.1175/1520-0469(1984)041<0981:TVOMHF>2.0.CO;2 |
| [] | Chang E K M, Orlanski I. 1993. On the dynamics of a storm track[J]. J. Atmos. Sci., 50(7): 999–1015. DOI:10.1175/1520-0469(1993)050<0999:OTDOAS>2.0.CO;2 |
| [] | 邓兴秀, 孙照渤. 1994. 北半球风暴轴的时间演变特征[J]. 南京气象学院学报, 17(2): 165–170. Deng Xingxiu, Sun Zhaobo. 1994. Characteristics of temporal evolution of northern storm tracks[J]. Journal of Nanjing Institute of Meteorology, 17(2): 165–170. |
| [] | Deser C, Walsh J E, Timlin M S. 2000. Arctic sea ice variability in the context of recent atmospheric circulation trends[J]. J. Climate, 13(3): 617–633. DOI:10.1175/1520-0442(2000)013<0617:ASIVIT>2.0.CO;2 |
| [] | Frederiksen C S, Frederiksen J S. 1993. Monsoon disturbances, intraseasonal oscillations, teleconnection patterns, blocking and storm tracks of the global atmosphere during January 1979:Linear theory[J]. J. Atmos. Sci., 50(10): 1349–1372. DOI:10.1175/1520-0469(1993)050<1349:MDIOTP>2.0.CO;2 |
| [] | Hakim G J. 2002. Developing wave packets in the north pacific storm track[J]. Mon. Wea. Rev., 131(11): 2824–2837. DOI:10.1175/1520-0493(2003)131<2824:DWPITN>2.0.CO;2 |
| [] | Hoskins B J, James I N, White G H. 1983. The shape, propagation and mean flow interaction of large-scale weather systems[J]. J. Atmos. Sci., 40(7): 1595–1612. DOI:10.1175/1520-0469(1983)040<1595:TSPAMF>2.0.CO;2 |
| [] | Hoskins B J, Valdes P J. 1990. On the existence of storm-tracks[J]. J. Atmos. Sci., 47(5): 1854–1864. DOI:10.1175/1520-0469(1990)047<1854:OTEOST>2.0.CO;2 |
| [] | Illari L, Marshall J C. 1983. On the interpretation of eddy fluxes during a blocking episode[J]. J. Atmos. Sci., 40(9): 2232–2242. DOI:10.1175/1520-0469(1983)040<2232:OTIOEF>2.0.CO;2 |
| [] | Jiang T Y, Deng Y, Li W H. 2013. Local kinetic energy budget of high-frequency and intermediate-frequency eddies:Winter climatology and interannual variability[J]. Climate Dyn., 41: 961–976. DOI:10.1007/s00382-013-1684-1 |
| [] | Lau N C. 1978. On the three-dimensional structure of the observed transient eddy statistics of the northern Hemisphere wintertime circulation[J]. J. Atmos. Sci., 35(10): 1854–1864. DOI:10.1175/1520-0469(1978)035<1900:OTTDSO>2.0.CO;2 |
| [] | Lee S. 1995. Linear modes and storm tracks in a two-level primitive equation model[J]. J. Atmos. Sci., 52(11): 1841–1862. DOI:10.1175/1520-0469(1995)052<1841:LMASTI>2.0.CO;2 |
| [] | Lee W J, Mak M. 1995. Dynamics of storm tracks:A linear instability perspective[J]. J. Atmos. Sci., 52(6): 697–723. DOI:10.1175/1520-0469(1995)052<0697:DOSTAL>2.0.CO;2 |
| [] | Luo D H, Diao Y N, Feldstein SB. 2011. The variability of the atlantic storm track and the north atlantic oscillation:a link between intraseasonal and interannual variability[J]. J. Atmos. Sci., 68(3): 577–601. DOI:10.1175/2010JAS3579.1 |
| [] | Nakamura H, Nakamura M, Anderson J L. 1997. The role of high-and low-frequency dynamics in blocking formation[J]. Mon. Wea. Rev., 125(9): 2074–2093. DOI:10.1175/1520-0493(1997)125<2074:TROHAL>2.0.CO;2 |
| [] | Orlanski I. 1997. Poleward deflection of storm tracks[J]. J. Atmos. Sci., 55(16): 2577–2602. |
| [] | Orlanski I, Gross B. 1999. The life cycle of baroclinic eddies in a storm track environment[J]. J. Atmos. Sci., 57(21): 3498–3513. DOI:10.1175/1520-0469(2000)057<3498:TLCOBE>2.0.CO;2 |
| [] | Orlanski I, Katzfey J. 1990. The life cycle of a cyclone wave in the Southern Hemisphere. Part 1:Eddy energy buget[J]. J. Atmos. Sci., 48(17): 1972–1998. DOI:10.1175/1520-0469(1991)048<1972:TLCOAC>2.0.CO;2 |
| [] | Overland J E, Pease C H. 1982. Cyclone climatology of the Bering Sea and its relation to sea ice extent[J]. Mon. Wea. Rev., 110(1): 5–13. DOI:10.1175/1520-0493(1982)110<0005:CCOTBS>2.0.CO;2 |
| [] | Simmons A J, Hoskins B J. 1978. The life cycles of some nonlinear baroclinic waves[J]. J. Atmos. Sci., 85(3): 441–452. DOI:10.1175/1520-0469(1978)035<0414:TLCOSN>2.0.CO;2 |
| [] | 孙照渤, 朱伟军. 2000. 冬季北半球风暴轴能量演变的个例分析[J]. 南京气象学院学报, 23(2): 147–155. Sun Zhaobo, Zhu Weijun. 2000. A case study of energy temporal variation for synoptic disturbances over the northern winter storm track[J]. Journal of Nanjing Institute of Meteorology, 23(2): 147–155. DOI:10.3969/j.issn.1674-7097.2000.02.001 |
| [] | 曾鼎文, 朱伟军, 李耀辉, 等. 2015. 冬季北大西洋风暴轴的东西变化及其能量诊断[J]. 气象科学, 35(6): 692–700. Zeng Dingwen, Zhu Weijun, Li Yaohui, et al. 2015. Zonal variations and its energy budget analysis of North Atlantic storm track in winter[J]. Journal of the Meteorological Sciences, 35(6): 692–700. DOI:10.3969/2014jms.0075 |
| [] | 朱伟军, 孙照渤. 1999. 风暴轴的研究[J]. 南京气象学院学报, 22(1): 121–127. Zhu Weijun, Sun Zhaobo. 1999. A review on storm track research[J]. Journal of Nanjing Institute of Meteorology, 22(1): 121–127. |
| [] | 朱伟军, 孙照勃. 2001. 涡动非地转位势通量对风暴轴维持的影响[J]. 大气科学, 25(1): 71–78. Zhu Weijun, Sun Zhaobo. 2001. Effects of eddy ageostrophic geopotential fluxes on the maintenance of storm tracks[J]. Chinese Journal of Atmospheric Sciences, 25(1): 71–78. DOI:10.3878/j.issn.1006-9895.2001.01.07 |
 2017, Vol. 22
2017, Vol. 22

